Fig. 1.

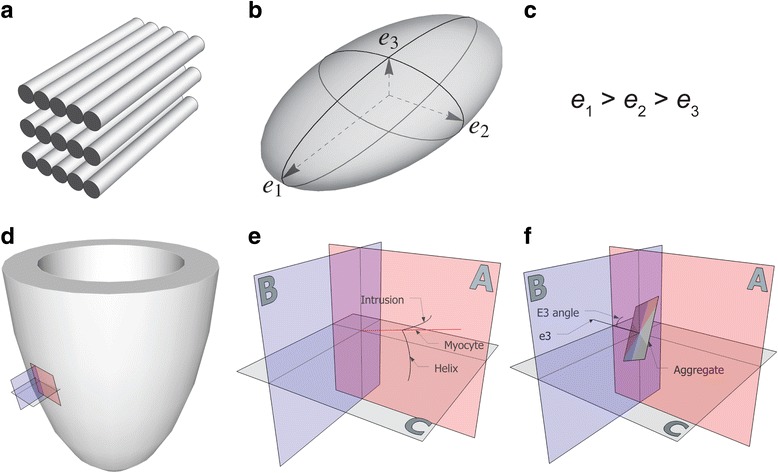
Diffusion tensor and eigenvectors. The shape of the diffusion tensor in an ordered fibrous environment such as the myocardium. Panel a depicts the schematic ordering of the cardiomyocytes while panel b shows the coherent shape of the diffusion tensor, the primary (e1), secondary (e2) and tertiary (e3) eigenvectors are shown along with their relationship in panel c. Panel d shows a schematic representation of the left ventricle with the local orthogonal planes aligned relative to the epicardium. Panel e shows the local set of orthogonal planes as superimposed in every voxel. Plane A (red) is the circumferential-longitudinal plane parallel to the epicardial tangential plane and plane B (blue) is the radial-longitudinal plane parallel to the left ventricular long axis and orthogonal to plane A. Plane C, the local “horizontal” plane, is the circumferential-radial plane orthogonal to planes A and B. The helical angle is the angle between the cardiomyocyte and plane C. The intrusion angle is the angle between the cardiomyocyte and plane A. Panel f shows the E3 angle as measured using the tertiary eigenvector (e3) relative to plane B. The aggregation of cardiomyocytes is depicted as a flat square, which is a gross oversimplification