Indentation Mapping Reveals Poroelastic, but not Viscoelastic, Properties Spanning Native Zonal Articular Cartilage

Abstract

Osteoarthrosis is a debilitating disease affecting millions, yet engineering materials for cartilage regeneration has proven difficult because of the complex microstructure of this tissue. Articular cartilage, like many biological tissues, produces a time-dependent response to mechanical load that is critical to cell’s physiological function in part due to solid and fluid phase interactions and property variations across multiple length scales. Recreating the time-dependent strain and fluid flow may be critical for successfully engineering replacement tissues but thus far has largely been neglected. Here, microindentation is used to accomplish three objectives: (1) quantify a materials time-dependent mechanical response, (2) map material properties at a cellular relevant length scale throughout zonal articular cartilage, (3) and elucidate the underlying viscoelastic, poroelastic, and nonlinear poroelastic causes of deformation in articular cartilage. Untreated and trypsin-treated cartilage were sectioned perpendicular to the articular surface and indentation was used to evaluate properties throughout zonal cartilage on the cut surface. The experimental results demonstrated that within all cartilage zones, the mechanical response was well represented by a model assuming nonlinear biphasic behavior and did not follow conventional viscoelastic or linear poroelastic models. Additionally, 10% (w/w) agarose was tested and, as anticipated, behaved as a linear poroelastic material. The approach outlined here provides a method, applicable to many tissues and biomaterials, which reveals and quantifies the underlying causes of time-dependent deformation, elucidates key aspects of material structure and function, and that can be used to provide important inputs for computational models and targets for tissue engineering.

1. Introduction

Biological tissues, e.g. cartilage, present significant property differences over small (i.e., nano- to micrometer) length scales and marked time-dependent behavior. Accurate determination of properties and their variation throughout tissues is vital to engineer materials that effectively recapitulate the property gradients that are present in native tissues, e.g. to match cellular level strains particularly under dynamic mechanical loading and to provide appropriate mechanical cues to cells. Much work thus far has focused on creating simple constructs that match bulk tissue properties at very slow loading rates, yet this approach neglects the dramatically different properties observed at higher physiological loading rates and the complex, hierarchical organization of most tissues that spans multiple length scales (e.g., nanometers to centimeters).

Articular cartilage is particularly compelling due to the prevalence of osteoarthritis and as a complex material possessing significant mechanical property variation, underlying chemistry, and extracellular matrix organization from the articular surface to the underlying bone [1–7]. While articular cartilage possesses a pronounced time-dependent response [8,9], classic methods for mechanical property assessment [10,11] and evaluating fluid-structure interactions [12–14] poorly assess behavior within small regions of tissue, e.g., within individual cartilage zones. Displacements of chondrocytes in cartilage sections have been mapped via digital image correlation [5,6,15], or through the use of displacement-encoded magnetic resonance imaging [16,17]; however, these methods apply loads to bulk sections of tissue and prevents direct loading of specific cartilage zones. Thus, while inverse methods have been applied to estimate properties, the quantification of time-dependent mechanisms remains daunting and prone to error. In contrast, microindentation provides a facile way to directly observe the mechanical response of cartilage in situ without altering the zonal arrangement, while enabling investigation of both elastic and time-dependent material behaviors.

The time-dependent response in articular cartilage has been attributed to viscoelasticity, poroelasticity, or a combination of these phenomenon [18–23]. Yet it is likely that these behaviors vary with the underlying chemistry and extracellular matrix organization in zonal cartilage. Indentation of the articular surface has evaluated equilibrium properties of native, diseased, and repair cartilage [24–28] and begun to explore the time-dependent response [9,22,29,30]. Results were combined with finite element models [21,31] and correlated with chemistry in maps spanning osteochondral tissues [32–34]. However, much work remains to establish time-dependent material properties for each cartilage zone.

Microindentation uniquely provides the ability to assess both time-dependent behavior in small tissue volumes and the underlying causes of this deformation at length scales relevant to cells. Because viscoelastic models assume that materials act as a continuum, mechanical response is assumed to be independent of indenter probe radius if the applied strain and strain rates are kept constant [35]. Thus if the rise (i.e. indentation) time and the ratio of indenter depth to indenter radius are maintained, then the measured material parameters should not vary with indenter size. On the other hand, because poroelastic models assume that a time-dependent response is due to fluid transport, the size of the indenter has a nonlinear impact on the behavior of the tested material. For this poroelastic case, a characteristic rise time can be established which is proportional to the square of the indentation radius if relative indentation depth is kept constant [36,37]. Thus, testing at various indentation rates using multiple sizes of indenter probes with rates matched via viscoelastic or poroelastic assumptions can determine whether time-dependent material behavior is due physical arrangement of the solid material (i.e. viscoelasticity) or fluid transport (i.e. poroelasticity). With data obtained by performing experiments using multiple sized probes, we can now evaluate whether viscoelastic [38] or poroelastic [9,36] models better represent cartilage behavior in each zone.

Using a novel microindentation-based approach, we test the hypothesis that a nonlinear biphasic model [9] best represents the time-dependent mechanical behavior of articular cartilage. Trypsin treatment was also employed to increase permeability through glycosaminoglycan (GAG) depletion [39,40] to evaluate changes in the time-dependent mechanical response, with increased permeability of cartilage, with the goal of deconvoluting viscoelastic and poroelastic behavior. In this work we performed indentation using multiple sized indenters and multiple initial loading rates for untreated cartilage, trypsin treated cartilage, and agarose. The indentation modulus was obtained from the initial portion of the load/displacement response and used to determine the dominant time dependent mechanism (poroelastic vs. viscoelastic). The load relaxation data was then fit using the appropriate class of material models. Additionally the nonlinear biphasic model was fit using a multiple indent approach to compensate for finite loading rates. Evaluating zonal material properties provides an important target for tissue engineering to match deformations and fluid flows experienced by cells in native tissue, to improve accuracy of computational finite element models of cartilage, and may provide novel insight into osteoarthritis progression.

2. Methods

2.1 Materials

Agarose, selected as a material with known poroelastic behavior [41], samples were prepared (Sigma, A9539) to 10% (w/w), dissolved into phosphate buffered saline (PBS) with a pH of 7.4, heated to 90°C in a double boiler while being continuously mixed with a magnetic stir rod, and centrifuged (2500 RPM, 5 minutes) to eliminate bubbles. Eight specimens were sectioned using a vibratome (Technical Products International, Vibratome 1000) to 1 mm thick slices and mounted to 1 mm thick steel testing pucks using a thin layer of cyanoacrylate.

Separately, cartilage samples were collected from three Yorkshire pigs of 2.5–4 months in age from the lateral femoral condyle using an 8.5 mm mosaicplasty tubular chisel (Smith & Nephew, 7207494). The Massachusetts General Hospital (MGH) Institutional Animal Care and Use Committee (IACUC) approved all procedures. The split-line direction was determined by inserting a pin in the center of the cartilage plug [42]. Cartilage was cut from the bone and sectioned to ~500 µm thick slices parallel to the split-line direction using a vibratome. Subsequent slices were set apart for microindentation, Secondary Harmonic Generation (SHG) and Two Photon Fluorescence (TPF) imaging and histology (Figure 1). Cartilage sections were indented or prepared for histology without further treatment (n=6) or subjected to enzymatic degradation for three hours in 0.5% Trypsin (Life Technologies, 15090046) in calcium and magnesium free Hanks Balanced Saline Solution (Life Technologies, 14175079) and thoroughly rinsed in PBS (n=6). For mechanical testing, samples were mounted on 1mm thick steel testing pucks using a thin cyanoacrylate layer and submerged in with 1× PBS containing 1% (v/v) Protease Inhibitors (PI) (Halt, Thermo Fisher 78438).

Figure 1.

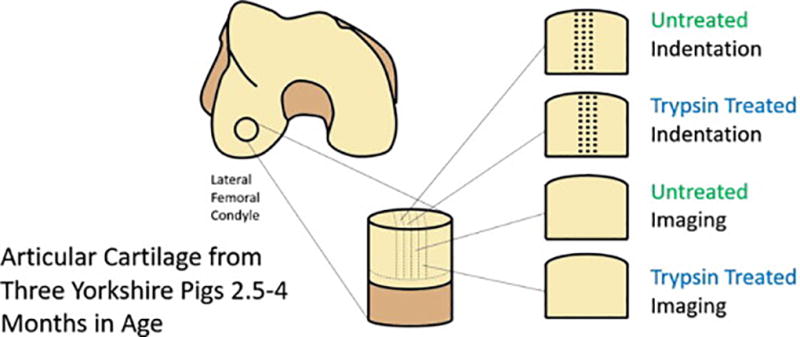
Excise location and sample groups for articular cartilage. Dots on indentation samples represent indentation arrays performed parallel to the articular surface.

2.2 Histological analysis and SHG/TPF Imaging

Cartilage sections were fixed in 4% paraformaldehyde, dehydrated, paraffin embedded, and sectioned to 10 µm thick slices using a microtome. These slices were stained with safranin-O/Fast Green to visualize sulfated GAGs. The prevalence of type II collagen in cartilage was investigated using SHG and TPF (Coherent Chameleon Ultra II laser tuned to 800 nm wavelength). A dichroic mirror was used to separate the output onto a non-descanned QUASAR Detection Unit with two detectors enabling the observation of SHG and two photon emissions separately. Imaging was performed on 500 µm thick samples without staining or contrast agents.

2.3 Microindentation testing

Microindentation was performed on a Hysitron TI-950 nanoindenter. Indent arrays using cono-spherical probes (R = 104.7 µm and 250.1 µm) were spaced at a minimum of 3 × the indenter contact radius. Two 25 indent arrays were performed for each test condition in agarose, whereas in cartilage arrays spanned from the articular surface toward the bone (R = 104.7 µm: 4 × 18 array at 100 µm spacing in x- and y-; R = 250.1 µm: 3 × 11 array at 170 µm spacing). Additionally, 25 indents were placed on the articular cartilage gliding surface in treated (n = 4) and untreated (n = 4) samples.

All indents were performed in displacement control to a max indentation depth of 5% of the probe radius (Figure 2). Multiple load rates were tested with each indenter using a trapezoidal load-hold unload function. The rise times (t_R) were 0.32, and 2 s for the R = 104.7 µm probe and 2 and 12.5 s for the R = 250.1 µm radius probe. Multiple rise times were employed to create matched strain rates and poroelastic flow rates for the different sized indenters. The samples were then subjected to a 40 second stress relaxation hold, corresponding to load relaxation rates of approximately 1 µN/s, which is 1,200–11,000 times less than initial relaxation rates for these materials, and unloaded at the same rate as they had been loaded.

Figure 2.

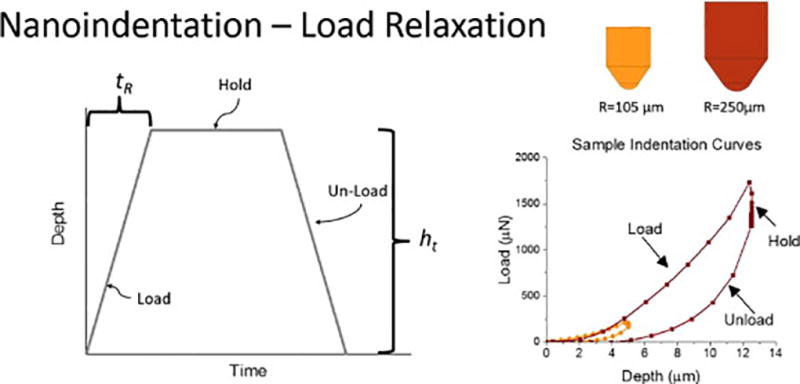
Microindentation relaxation test load profile, indenter probe geometry, and representative indentation curves which demonstrate matched strain fields for different sized indenters

All indents were accomplished at large indentation depths and we assumed a perfect spherical geometry for the indenters. To determine the exact point of initial surface contact, we followed the method outlined by Guo [43]. In brief, a small (5 µN) load was used to determine when the probe made contact with the sample but this creates a non-negligible deformation in the sample. The Hertz formula was rearranged for contact between two elastic materials assuming that the material modulus remained constant with indentation depth. Experimental indentation load two-thirds power versus indentation depth was then used to calculate the indentation modulus and this in turn was used to predict the indenter position at zero load.

2.4 Microindentation Analysis

For comparison between viscoelastic and poroelastic model assumptions, Hertz [44,45] analysis of the initial loading curve was performed. The indentation modulus (E^*) is reported without conversion to the elastic modulus (E) via the Poisson’s ratio (ν) of the tested material. Because no appreciable plastic deformation was observed, elastic-plastic [46,47] models were not applied. Rather, three time-dependent models were investigated [48–50] which incorporate two broad categories of underlying physical mechanisms: viscoelastic, single phase with time-dependence resulting from changes in molecular arrangement, and poroelastic, the tested material is made up of separate solid and fluid phases [3,48,49,51] where time-dependence results from fluid transport.

To evaluate for viscoelastic behavior, we utilized a method that relates the shear relaxation modulus of the tested material (G), to the instantaneous (G₀) and long-term shear modulus (G_∞) using the Poisson’s ratio (ν), relaxation coefficients and time constants [38]. For biphasic poroelastic behavior, two models that have been previously applied to cartilage were considered. The first model, proposed by Hu et al. [36], assumes that the solid phase behaves as a linear elastic material and that all the time-dependent response can be attributed to the flow of the fluid phase through the material. Fitting the relaxation curve produces measures of G, ν, and permeability (k). An alternate assumption is that the Poisson’s ratio of the tested material is near zero and that the solid phase behaves linear elastically in compression and tension but with different moduli for each. This latter approach was proposed by Soltz and Ateshian [52] and applied to indentation by Burris et al. [9,53–55], fitting this nonlinear biphasic theory, sometimes termed “Hertz Burris Theory” (HBT), produces measures of tensile modulus (E_t), equilibrium contact modulus (E_c0) and k.

The poroelastic indentation models are based on the assumption that loading occurs very quickly. If loading occurs at a rate that is not fast enough to create significant fluid pressure, the poroelastic models are not able to directly assess material properties from one single indentation test. Under this scenario, the HBT model underestimates the tensile modulus while the linear biphasic model overestimates the Poisson’s ratio. To overcome this limitation, we performed indentation tests at multiple loading rates and with different sized indenters. This compensation for finite loading rate enabled us to determine the portion of the load supported by the fluid, or fluid load fraction, which was then used to predict the material parameters following methods developed by Bonnevie et. al. [9].

2.5 Atomic Force Microscopy

Atomic force microscopy (AFM) was performed on an Asylum Cypher AFM to visualize and measure the topography of representative regions on both the untreated and trypsin-treated cartilage surfaces. Measurements were conducted in PBS at 25 °C using the droplet cantilever holder and stage. Triangular SiN cantilevers (Bruker SNL-10) with sharp Si tips (R ≈ 2 nm) were used to maximize the spatial resolution of the images. Each probe was calibrated using the thermal fluctuation method [56]; the resulting values for the spring constant of the probe varied from 0.07 N/m to 0.18 N/m. Moreover, we utilized the Fast Force Mapping Mode to concurrently minimize acquisition times, such that 10 µm × 2.5 µm images with 256 pixels × 64 pixels (≈ 40 nm pixel size) were possible in about 30 min. The maximum force and ramp rate for image acquisition were 10 nN and 20 Hz, respectively. Cross-sectional height data were taken from selected locations to compare the surface topography before and after the trypsin treatment.

2.6 Statistical Analysis

Statistical analysis was performed using Minitab v.17 (State College, PA). For agarose, one-way ANOVA compared poroelastic or viscoelastic test conditions. E* was transformed to the power of −2 to satisfy model assumptions of normally distributed residuals and homoscedasticity. Post-hoc comparisons were performed with Bonferroni’s test with critical alpha set as 0.05/2 = 0.025. For cartilage, three-factor ANOVA evaluated factors of treatment (trypsin or untreated), region (superficial, middle, or deep) and test condition (baseline, viscoelastic, or poroelastic), as well as interactions. E* was log-transformed to satisfy model assumptions of normally distributed residuals and homoscedasticity. Post-hoc comparisons were performed with Bonferroni’s test with critical alpha set as 0.05/12 = 0.004. Numerical results are presented as mean ± SD; graphical results are mean with SD as error bars.

3. Results

Initial indentation modulus was used to compare matched strain rates (i.e. viscoelastic assumptions) or matched characteristic poroelastic indentation rate (i.e. poroelastic assumptions [36,37], see supplemental material) using two cono-spherical indenters of different radii. Mean R^2 values for the Hertzian fitting of the indentation data demonstrated validity of this approach as follows: Untreated − 0.993 ± 0.017, Trypsin Treated − 0.988 ± 0.017, and Agarose − 0.998 ± 0.0028. Indentation of agarose gels produced an indentation modulus of 1.82 ± 0.16 MPa for the R = 105 µm probe. When tested with the R = 250 µm probe at an equal strain rate the indentation modulus was significantly higher at 2.32 ± 0.24 MPa, p<0.001. However, testing using a matched poroelastic indentation rate for the R = 250 µm probe produced a modulus of 1.84 ± 0.16 MPa which is nearly identical to that found using the smaller probe (Figure 3).

Figure 3.

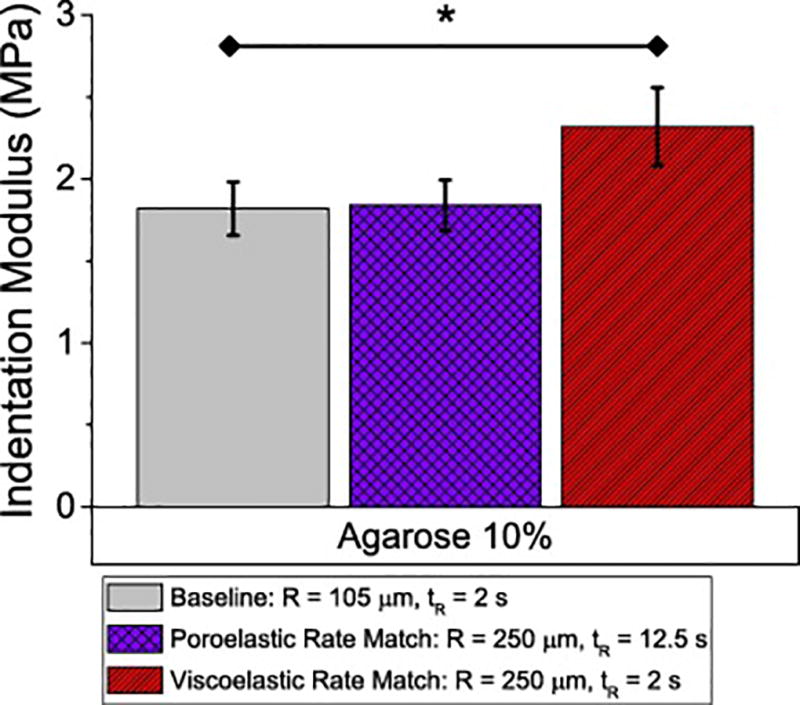
Indentation modulus of agarose demonstrates behavior of a material with time-dependent behavior dominated by poroelasticity. Hertz analysis performed on the loading portion of the indentation curve. *=p<0.05

For the cartilage samples, the indentation modulus was mapped over a 400 × 1800 µm field. For clarity, properties at four test locations will be presented first (i.e. on the articular surface, and at ~250, ~1050, and ~1750 µm from the articular surface). Matched strain rates produced significantly different indentation moduli for the untreated cartilage throughout the cartilage thickness (i.e. p=0.02, 0.002, and 0.004 for ~250, ~1050, and ~1750 µm locations, respectively) (Figure 4). By contrast, when poroelastic indentation rates were matched, the indentation moduli were not significantly different from the values measured with the smaller indenter. Indentation modulus obtained from testing the trypsin-treated cartilage showed a response with minimal time-dependence. The indentation modulus for trypsin-treated cartilage measured using the larger indenter did not provide a better correlation using matched strain rates or matched poroelastic indentation rate (Figure 4).

Figure 4.

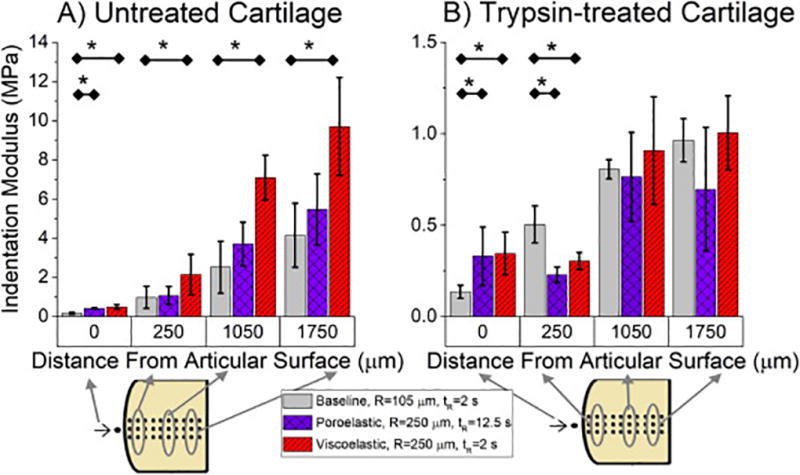
Indentation modulus of untreated and trypsin-treated cartilage on the articular surface and at three distances from the articular surface. Untreated cartilage behaves as a poroelastic material at all distances from the articular surface. By contrast, the underlying cause of time-dependence in trypsin-treated samples cannot be determined. Hertz analysis performed on the loading portion of the indentation curve. *=p<0.05

Investigation of time-dependent material properties was performed by fitting the various models to the relaxation data. Evaluating viscoelastic behavior alone produced inconsistent material parameters for agarose, untreated, and trypsin-treated cartilage (results not shown). Conversely, the Hu poroelastic model [36] provided stable measures for agarose material properties with a shear modulus (G) of 0.52 ± 0.17 MPa, Poisson's ratio (ν) of 0.26 ± 0.11, and permeability (k) of 4.66 ± 4.26 × 10⁻¹⁰m². No model proved superior for trypsin-treated cartilage samples (results not shown). The viscoelastic model produced inconsistent results when evaluating micromechanical behavior of untreated cartilage. Results obtained from the fitting the linear biphasic and nonlinear biphasic theory models were more consistent but still suffered from limitations due to the finite loading rate when applied using only load relaxation data. In the linear biphasic model, the Poisson’s ratio was found to approach the theoretical limit of negative one at maximum indentation rates.

The nonlinear biphasic theory was also applied using an approach to compensate for the finite loading rate, with material parameters for both untreated and trypsin-treated specimens in Figure 5. The tensile and compressive moduli of the untreated cartilage were markedly higher than the moduli of the trypsin-treated samples. The compressive and tensile moduli increased in both treatment groups at greater distances from the articular surface. The permeability for both untreated and treated samples decreased rapidly for approximately the first 500 µm from the articular surface and then decreased more slowly throughout the remainder of the thickness, whereas permeability of the trypsin-treated cartilage was significantly greater than untreated cartilage at all test locations.

Figure 5.

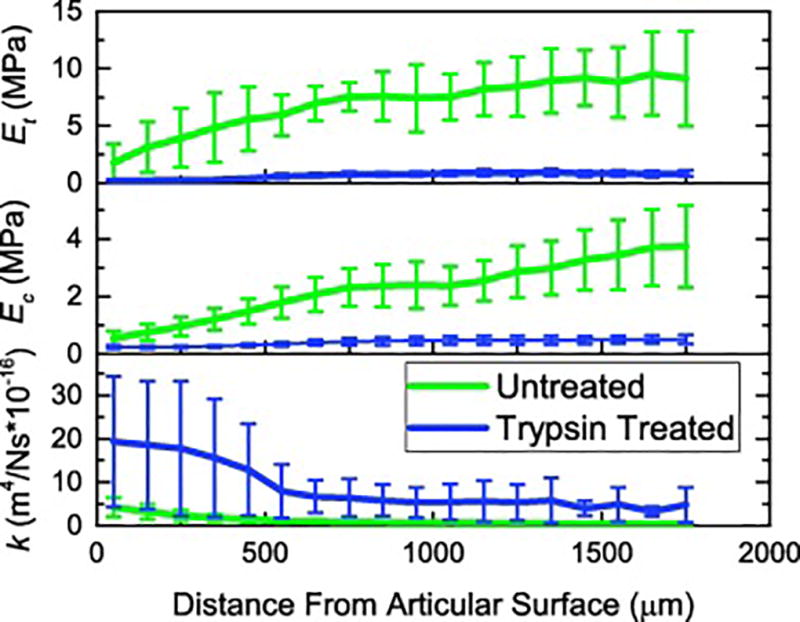
The tensile and compressive modulus decrease while the permeability increases for untreated and trypsin-treated cartilage as a function of distance from the articular surface. Trypsin treatment decreases tensile and compressive modulus while increasing permeability for all cartilage zones. Parameters obtained from rate compensated nonlinear biphasic theory using indents performed at multiple displacement rates.

Histological staining of cartilage samples provided a qualitative measure of the effects of trypsin digestion. The safranin-O/Fast Green stain showed substantially less GAG content in the trypsin-treated samples when compared to the untreated cartilage (Figure 6). However, staining indicating GAG and collagen content varied little with distance from the articular surface. While not quantitative, SHG imaging of cartilage demonstrated no difference in the prevalence of signal from type II collagen (Figure 6).

Figure 6.

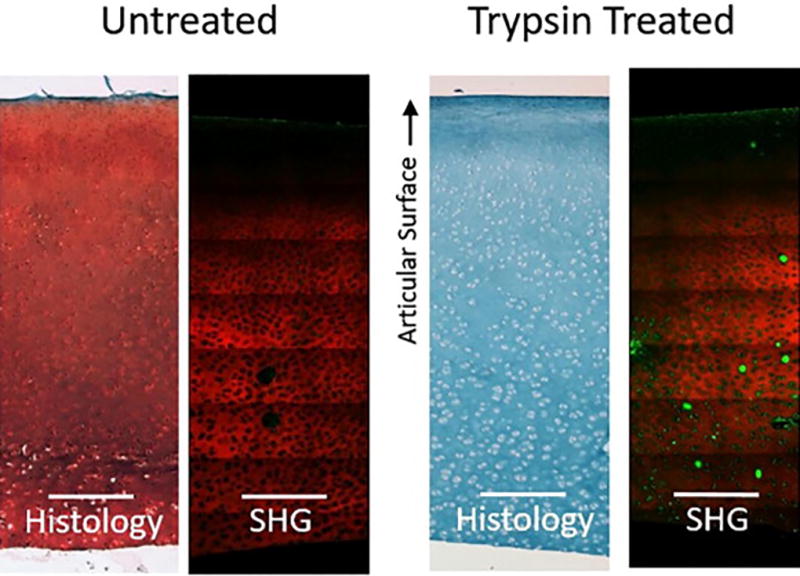
Histology and SHG/TPF images of articular cartilage demonstrate GAG depletion due to trypsin treatment but little change to collagen matrix. Safranin-O/Fast Green histological stain on paraffin embedded samples. Fresh samples imaged with SHG for collagen type II artificially colored red and TPF artificially colored green.

Due to the high spatial resolution of AFM, topography scans of small regions of cartilage evaluated features of the collagen matrix that would be unresolvable using microindentation with large spheres. Indentation modulus testing was not performed using the AFM because the small scan size did not permit evaluation of the entire region of interest. Scans of the middle zone of untreated and trypsin-treated cartilage revealed differences in collagen network alignment and linearity (Figure 7). Collagen fibers in untreated samples appear more uniformly aligned and tightly packed compared to the trypsin treated samples.

Figure 7.

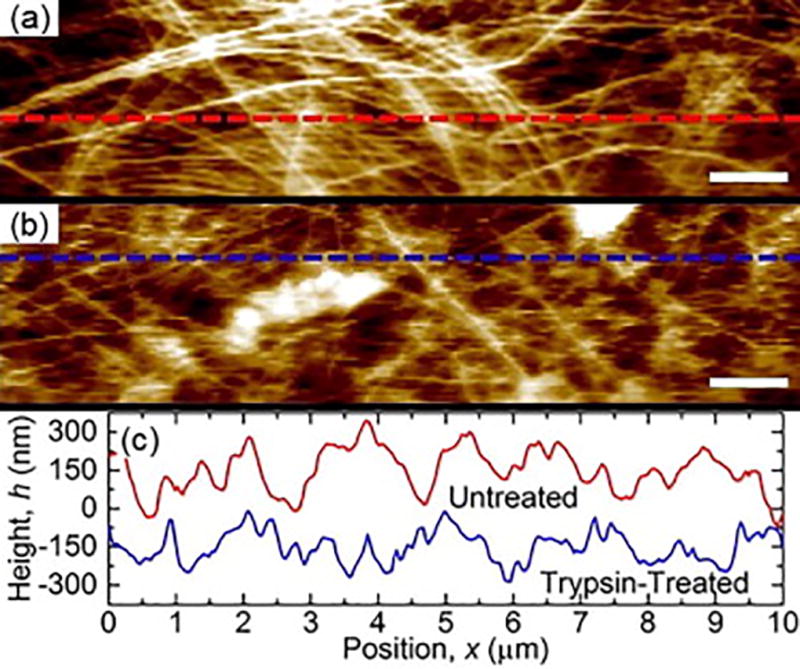
Decreased organization of collagen matrix is observed via atomic force microscopy, topography images of untreated (a) and trypsin-treated cartilage (b). Images were taken approximately 1000 µm from the articular surface. In (a) and (b) white indicates higher and black lower topography. Scale bar = 1 µm

Additionally, heat maps representing tensile modulus, compressive modulus, and permeability of a representative sample were produced are shown in Figure 8. In agreement with the trends observed in averaged data, these maps show functional gradients in E_t and E_c0 and k and changes resulting from trypsin treatment. In addition, these figures demonstrate the capability of nanoindentation to provide maps of material properties with high spatial resolution over a large area even for soft materials.

Figure 8.

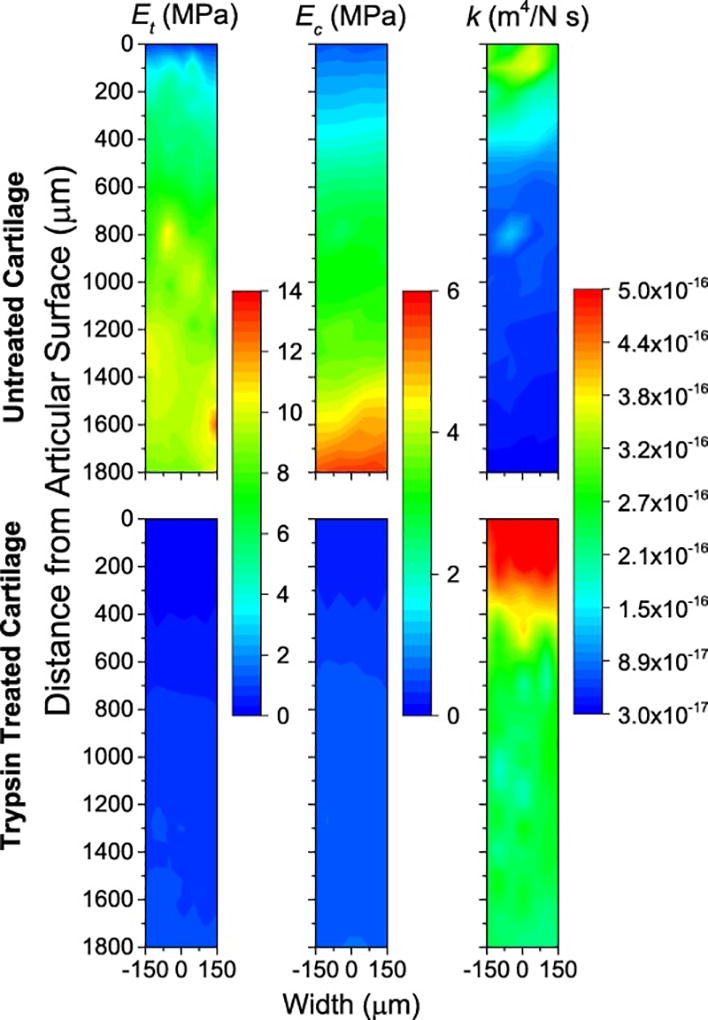
Heat maps of mechanical properties obtained from indentation rate compensated nonlinear biphasic theory demonstrate variation in mechanical properties with distance from the articular surface and treatment. Representative untreated and trypsin-treated cartilage samples.

4. Discussion

Biological and biomimetic materials frequently present significant property differences over small length scales and a pronounced time-dependent response producing vastly different mechanical properties at physiological loading rates compared to equilibrium properties. The approach presented herein represents a systematic method to investigate and quantify these properties to provide invaluable information for those seeking to recapitulate native mechanosensory cues for cells. Using microindentation, we mapped tensile modulus, compressive modulus, and permeability of articular cartilage at sub-millimeter length scales with an intact zonal structure. We also addressed a longstanding question that has previously been difficult via bulk mechanical testing: we found that the time-dependent behavior in articular cartilage results from a predominately poroelastic, rather than viscoelastic, mechanisms throughout all cartilage zones. This work provides important design targets for approaches attempting to reproduce physiological conditions via tissue engineering.

To establish the validity of these methods a material known to possess linear poroelastic behavior was tested. In agreement with the findings of Strange et. al. [41], agarose was best modeled as a linear biphasic material and experimental results directly contradict viscoelastic assumptions. While the equilibrium modulus of agarose is similar to that of cartilage, the short time response is dramatically different. Agarose provides an ideal example of why small scale, complex properties may impact mechanobiology. Even if equilibrium modulus and permeability were tailored to match cartilage tissue properties, encapsulated cells would experience markedly different strains and fluid flow during dynamic loading. Similar results would be anticipated with most hydrogels and other materials commonly used for tissue engineering, thus highlighting the critical importance of accurately measuring native tissue and reproducing mechanical properties in synthetic materials for tissue engineering.

Despite the common notion that cartilage behaves viscoelastically, microindentation clearly demonstrated poroelastic behavior throughout all cartilage zones. Further, the poroelastic linear biphasic model is also insufficient as it produces an increasingly negative Poisson’s ratio with increasing strain rate. This negative Poisson’s ratio is not consistent with linear biphasic theory [57] or macroscopic cartilage testing which produces a Poisson's ratio of 0 – 0.2 [52,58,59]. The non-linear biphasic, overcomes this limitation by fixing the Poisson’s ratio at zero and allowing the tensile modulus of the material to exceed the compressive modulus and allow for higher load support at fast loading rates. The properties measured for cartilage were found to be well represented by nonlinear biphasic theory in all zones.

The material properties observed herein for tensile modulus, compressive modulus, and permeability of cartilage are similar to those found for bulk cartilage samples. Time-dependent properties have also been observed through macro-scale indentation testing by Bonnevie et al. [9], fluid load fraction observed by Park et al. [60], and permeability observed by Soltz and Ateshian [52]. Additionally, equilibrium properties of cartilage compressive [8,52,55,61] and tensile moduli [9,52,61,62] from indentation testing are similar to values found for bulk cartilage testing (e.g., E_t = 12.75 MPa [52], E_c = 0.079 MPa in the superficial zone to 2.1 MPa in the deepest zone [4], and k = 6.06 × 10–16 m4/N▪ s [52] as compared to data presented in Figure 6). Despite significant limitations due to loading rate constraints, the elastic properties observed herein, using nonlinear biphasic theory, are strikingly consistent with the properties observed by others from uniaxial testing, which lacks these same model limitations. These comparisons are also notable because testing was not only performed at different length scales but also on cartilage from different ages and species and ages of animals.

In addition to validating previous measures, this work quantified changes in nonlinear poroelastic properties with distance from the articular surface. Specifically, the tensile and compressive moduli increased through the thickness of the cartilage, and the permeability decreased (Figure 5). These property variations with distance may result from zonal differences in chemistry and structure. One measure of chemical heterogeneity is observed in the decreased SHG signal present in the superficial zone, which confirmed observations from picrosirius red stain/helium ion microscopy [63]. The decreased SHG signal indicates reduced crystallinity and collagen fibril alignment, and correlates with the lower moduli and increased permeability observed in the superficial zone. To facilitate translation to tissue engineering and computational modeling, mathematical functions representing the property variation were fit to the experimental results (supplementary data).

Further insight into the chemical and structural characteristics responsible for the time-dependent behavior of cartilage was gained by evaluating trypsin treated samples. The tensile and compressive moduli were decreased in addition to substantially increased permeability with trypsin treatment. These changes can directly be attributed to the absence of GAGs [11]. Further, one potential explanation for decreased tensile modulus lies in the high osmotic pressure in untreated cartilage, which exerts a static tensile load on the collagen network. Conversely in enzyme-treated cartilage, GAG depletion and low osmotic pressure allows relaxation of the collagen network. GAG depleted cartilage has been shown to exhibit a pronounced “toe” region in the stress-strain response which is absent in untreated cartilage [64]. This hypothesis is further supported herein by AFM topography images that reveal a more tightly aligned collagen network in untreated samples compared to trypsin-treated samples confirming prior observations [65]. Moreover, GAG depletion, which parallels tissue changes in osteoarthritis, would likely result in increased compressive strain and fluid flow which may attribute to cell death and further progression of the disease [58]–[60].

This work produced key insights into the zonal behavior of articular cartilage and was an important step toward establishing design targets for tissue engineering. Further efforts should be put forward to apply these methods to tissues from a statistically representative number of skeletally mature human subjects. Additionally, as trypsin treatment may have resulted in degradation of the collagen network and removal of GAGs that may not precisely mimic disease, evaluating arthritic tissue would provide valuable insight. Finally, due to load rate limitations of the indenter, a more direct method of assessing material properties would be desirable by extending nonlinear biphasic theory to dynamic mechanical analysis or by incorporating a ramp correction factor. Another significant limitation of this work is that the models employed assume that time-dependent behavior arises from a single physical mechanism. This work identifies the dominant mechanism for this time-dependent response but actual tissue behavior may result from a combination of viscoelastic and poroelastic phenomena. A promising approach to correct for both finite loading rate and mixed poroelastic/viscoelastic behavior would be creation and application of finite element models of indentation of a nonlinear biphasic viscoelastic material. Collectively, these efforts represent critical advances toward creating tissue engineered constructs that can recreate the mechanical environment of native cells.

5. Conclusion

This study demonstrated a method to measure the time-dependent behavior of biological and biomimetic materials. This understanding is important to recreate the mechanical environment of native tissue and stimulate cells with physiologically relevant strains and fluid flow. Using indentation, we mapped property variation over cell relevant length scales within a tissue. Further, this approach illuminated the underlying poroelastic and or viscoelastic causes of time-dependence in articular cartilage where viscoelastic and linear biphasic models were insufficient. Instead, cartilage is best modeled as a nonlinear biphasic material. Additionally, tensile modulus, compressive modulus, and permeability of untreated and trypsin treated cartilage were quantitatively measured in zonal cartilage as a function of distance from the articular surface. These measurements provide invaluable information for tissue engineers seeking to recreate cartilage zonal structure, understand disease progression, and as inputs for computational finite element models.

Statement of Significance.

Elucidating the time-dependent mechanical behavior of cartilage, and other biological materials, is critical to adequately recapitulate native mechanosensory cues for cells. We used microindentation to map the time-dependent properties of untreated and trypsin treated cartilage throughout each cartilage zone. Unlike conventional approaches that combine viscoelastic and poroelastic behaviors into a single framework, we deconvoluted the mechanical response into separate contributions to time-dependent behavior. Poroelastic effects in all cartilage zones dominated the time-dependent behavior of articular cartilage, and a model that incorporates tension-compression nonlinearity best represents mechanical behavior. These results can be used to assess the success of regeneration and repair approaches, as design targets for tissue engineering, and for development of accurate computational models.