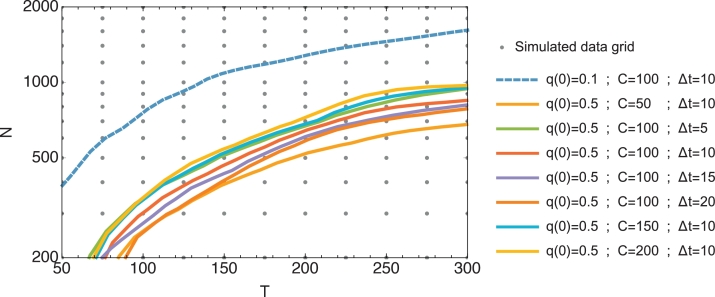
Fig. 2.
Potential to identify a Wright–Fisher model of evolution. Contours show lines of constant likelihood difference ΔL per locus per sampling instant by population size N and experimental duration T, between the exact Wright–Fisher and Gaussian drift models, when data is generated by Wright–Fisher propagation. Each contour represents the threshold below which correct model identification is possible at comparable likelihood differences. Solid lines show the contour ; a dashed line shows the contour for each set of parameters. Contours were found by interpolation of data generated at specific combinations of population size and experimental duration, shown as gray dots, and smoothing with an exponential moving average. Log scale is used on the y-axis.