One Size Doesn’t Fit All: Measuring Individual Privacy in Aggregate Genomic Data

Abstract

Even in the aggregate, genomic data can reveal sensitive information about individuals. We present a new model-based measure, PrivMAF, that provides provable privacy guarantees for aggregate data (namely minor allele frequencies) obtained from genomic studies. Unlike many previous measures that have been designed to measure the total privacy lost by all participants in a study, PrivMAF gives an individual privacy measure for each participant in the study, not just an average measure. These individual measures can then be combined to measure the worst case privacy loss in the study. Our measure also allows us to quantify the privacy gains achieved by perturbing the data, either by adding noise or binning. Our findings demonstrate that both perturbation approaches offer significant privacy gains. Moreover, we see that these privacy gains can be achieved while minimizing perturbation (and thus maximizing the utility) relative to stricter notions of privacy, such as differential privacy. We test PrivMAF using genotype data from the Wellcome Trust Case Control Consortium, providing a more nuanced understanding of the privacy risks involved in an actual genome-wide association studies. Interestingly, our analysis demonstrates that the privacy implications of releasing MAFs from a study can differ greatly from individual to individual. An implementation of our method is available at http://privmaf.csail.mit.edu.

I. Introduction

Recent research has shown that sharing aggregate genomic data, such as p-values, regression coefficients, and minor allele frequencies (MAFs) may compromise participant privacy in genomic studies [1], [2], [3], [4], [5]. In particular, Homer et al. showed that, given an individual‘s genotype and the MAFs of the study participants, an interested party can determine with high confidence if the individual participated in the study (recall that the MAF is the frequency with which the least common allele occurs at a particular location in the genome). Following the initial realization that aggregate data can be used to reveal information about study participants, subsequent work has led to even more powerful methods for determining if an individual participated in a study based on MAFs [5], [6], [7], [8], [9]. These methods work by comparing an individual‘s genotype to the MAF in a study and to the MAF in the background population. If their genotype is more similar to the MAF in the study, then it is likely that the individual was in the study. This raises a fundamental question: how do researchers know when it is safe to release aggregate genomic data?

To help answer this question we introduce a new model-based measure, PrivMAF, that provides provable privacy guarantees for MAF data obtained from genomic studies. Unlike many previous privacy measures, PrivMAF gives an individual privacy measure for each study participants, not just an average measure. These individual measures can then be combined to measure the worst case privacy loss in the study. Our measure also allows us to quantify the privacy gains achieved by perturbing the data, either by adding noise or binning.

Previous work

Several methods have been proposed to help determine when MAFs are safe to release. The simplest method– one suggested for regression coefficients [10]– is to just choose a certain number and release the MAFs for at most that many single nucleotide polymorphisms (SNPs, e.g. locations in the genome with multiple alleles). Sankararaman et al. [7] suggested calculating the sensitivity and specificity of the likelihood ratio test to help decide if the MAFs for a given dataset are safe to release. More recently, Craig et al. [11] advocated a similar approach, using the Positive Predictive Value (PPV) rather than sensitivity and specificity. These measures provide a powerful set of tools to help determine the amount of privacy lost after releasing a given dataset. One limitation of these approaches, however, is that they ignore the fact that a given piece of aggregate data might reveal different amounts of information about different individual study participants, and instead look at an average measure of privacy over all participants. For the unlucky few who lose a lot of privacy in a given study, a privacy guarantee for the average participant is not very comforting. This observation was hinted at by Im et al. [5] who noted that individuals who have extremely large or small values for a particular phenotype can be more readily re-identified using regression coefficients from GWAS studies than those with average phenotypes. The only sure way to avoid potentially harmful repercussions is to produce provable privacy guarantees for all participants when releasing sensitive research data.

Some researchers have recently suggested k-anonymity [12], [3], [13] or differential privacy [14], [15] based approaches, which allow release of a transformed version of the aggregate data in such a way that privacy is preserved. The idea behind these methods is that perturbing the data decreases the amount of private information released. Though such approaches do give improved privacy guarantees, they limit the usefulness of the results, as the data has often been perturbed beyond its usefulness; thus, there is a need to develop methods that perturb the data as little as possible in order to maximize its utility.

Identifying individuals whose genomic information has been included in an aggregate result can have real-world repercussions. Consider, for example, studies of the genetics of drug abuse [16]. If the MAFs of the cases (e.g. people who had abused drugs) were released, then knowing someone contributed genetic material would be enough to tell that they had abused drugs. Along the same lines, there have been numerous genome-wide association studies (GWAS) related to susceptibility to numerous STDs, including HIV [17]. Since many patients would want to keep their HIV status secret, these studies need to use care in deciding what kind of information they give away. Such privacy concerns have led the NIH and the Wellcome Trust, among others, to move genomic data from public databases to access-controlled repositories [18], [19], [20]. Such restrictions are clearly not optimal, since ready access to biomedical databases has been shown to enable a wide range of secondary research [21], [22].

Many types of biomedical research data may compromise individual‘s privacy, not just MAF [2], [23], [10], [24], [25], [26], [27]. For instance, even if we just limit ourselves to genomic data there are several broad categories of privacy challenges that depend on the particular data available, e.g. determining from an individuals genotype and aggregated data whether they participated in a GWAS study [4], from an individual‘s genotype whether they are in a gene-expression database [5], or, alternately, determining an individual‘s identity from just genotype and public demographic information [24].

Our Contribution

We introduce a privacy statistic, our measure PrivMAF, which provides provable privacy guarantees for all individuals in a given study when releasing MAFs for unperturbed or minimally perturbed (but still useful) data. The guarantee we give is straightforward: given only the MAFs and some knowledge about the background population, PrivMAF measures the probability of a particular individual being in the study. This guarantee implies that, if d is any individual and PrivMAF(d, MAF) is the score of our statistic, then, under reasonable assumptions, knowledge of the minor allele frequencies implies that d participated in the study with probability at most PrivMAF(d, MAF). Intuitively, this measure bounds how confident an adversary can be in concluding that a given individual is in our study cohort based off the available information.

Moreover, the PrivMAF framework can measure privacy gains achieved by perturbing MAF data. Even though it is preferential to release unperturbed MAFs, there may be situations in which releasing perturbed statistics is the only option that ensures the required level of privacy– such as when the number of SNPs whose data we want to release is very large. With this scenario in mind, PrivMAF can be modified to measure the amount of privacy lost when releasing perturbed MAFs. In particular, the statistic we obtain allows us to measure the privacy gained by adding noise to (common in differential privacy) or binning (truncating) the MAFs. To our knowledge, PrivMAF is the first method for measuring the amount of privacy gained by binning MAFs. In addition, our method shows that much less noise is necessary to achieve reasonable differential privacy guarantees, at the cost of adding realistic assumptions about what information potential adversaries have access to, thus providing more useful data.

In addition to developing PrivMAF, we apply our statistic to genotype data from the Wellcome Trust Case Control Consortium‘s (WTCCC) British Birth Cohorts genotype data. This allows us to demonstrate our method on both perturbed and unperturbed data. Moreover, we use PrivMAF to show that, as claimed above, different individuals in a study can experience very different levels of privacy loss after the release of MAFs.

II. METHODS

A. The Underlying Model

Our method assumes a model implicitly described by Craig et al. [11], with respect to how data were generated and what knowledge is publicly available.

PrivMAF assumes a large background population. Like previous works, we assume this population is at Hardy-Weinberg (H-W) equilibrium. We choose a subset (B) of this larger population, consisting of all individuals who might reasonably be believed to have participated in the study. Finally, the smallest set, denoted D, consists of all individuals who actually participated in the study. As an example, consider performing a GWAS study at a hospital in Britain. The underlying population might be all people of British ancestry; B, the set of all patients at the hospital; and D, all study participants.

As a technical aside, it should be noted that– breaking with standard conventions– we allow repetitions in D and B. Moreover, we assume that the elements in D and B are ordered.

In our model B is chosen uniformly at random from the underlying population, and D is chosen uniformly at random from B (we briefly address this assumption in the Appendix). An individual‘s genotype, d = (d₁, . . . , d_m), can be viewed as a vector in {0, 1, 2}^m, where m is the number of SNPs we are considering releasing. Let p_j be the minor allele frequency of SNP j in the underlying population. We assume that each of the SNPs is chosen independently. By definition of H-W equilibrium, for any d ∈ B, the probability that d_j = i for i ∈ {0, 1, 2} is $\left(\begin{array}{c}2\hfill \\ i\hfill \end{array}\right){(1-p_j)}^{2-i}{p}_j^i$.

Let ${\text{MAF}}_j(D)=\frac{1}{2n}\sum _{d\in D}{d}_j$ be the minor allele frequency of SNP j in D, the frequency with which the least common allele occurs at SNP j. Then MAF(D) = (MAF₁(D), . . . , MAF_m(D)). We assume the parameters, {p_i}_i, the size of B (denoted N), and the size of D (denoted n) are publicly known. We are trying to determine if releasing MAF(D) publicly will lead to a breach of privacy.

Note that our model does assume the SNPs are independent, even though this is not always the case due to linkage disequilibrium (LD). This independence assumption is made in most previous approaches. We can, however, extend PrivMAF to take into account LD by using a Markov Chain based model (see the Appendix). The original WTCCC paper [28] looked at the dependency between SNPs in their dataset and found that there are limited dependencies between close-by SNPs. In situations where LD is an issue one can often avoid such complications by picking one representative SNP for each locus in the genome.

B. Measuring Privacy of MAF

Consider an individual d ∈ B. We want to determine how likely it is that d ∈ D based on publicly released information. We assume that it is publicly known that d ∈ B. This is a realistic assumption, since it corresponds to an attacker believing that d may have participated in the study. This inspires us to use

$$P(d\in \tilde{D}|\text{MAF}(\tilde{D})=\text{MAF}(D),d\in \tilde{B})$$ (1)

as the measure of privacy for individual d, where D̃ and B̃ are drawn from the same distribution as D and B. Informally, D̃ and B̃ are random variables that represent our adversary‘s a priori knowledge about D and B.

More precisely, we calculate an upper bound on Equation 1, denoted by PrivMAF(d, MAF(D)). In practice we use the approximation:

$$\text{PrivMAF}(d,\text{MAF}(D))\approx \frac{1}{1+\frac{(N-n)P_n(x(D))}{n{P}_{n-1}(x(D)-d)}}$$

where x(D) = 2nMAF(D) and

$$P_n(x)=\prod _{i=1}^m\left(\begin{array}{c}2n\hfill \\ x_i\hfill \end{array}\right)p_i^{x_i}{(1-p_i)}^{2n-x_i}$$

It should be noted that, for reasonable parameters, this upper bound is almost tight. We can then let

$$\text{PrivMAF}(D)=\underset{d\in D}{\text{max}}\text{ PrivMAF}(d,\text{MAF}(D))$$

Informally, for all d ∈ D, PrivMAF(D) bounds the probability that d participated in our study given only publicly-available data and MAF(D). A sketch of the derivation is given in the Appendix.

This measure allows a user to choose some privacy parameter, α, and release the data if and only if PrivMAF(D) ≤ α. It is worth noting, however, that deciding whether or not to release the data gives away a little bit of information about D, which can weaken our privacy guarantee. While in practice this seems to be a minor issue, we develop a method to correct for it in the Appendix.

C. Measuring Privacy of Truncated Data

In order to deal with privacy concerns it is common to release perturbed versions of the data. This task can be achieved by adding noise (as in differential privacy), binning (truncating results), or using similar approaches. Here we show how PrivMAF can be extended to perturbed data.

We first consider truncated data. Let ${\text{MAF}}_j^{\text{trunc}(k)}(D)$ be obtained by taking the minor allele frequencies of the jth SNP and truncating it to k decimal digits. For example, if k = 1 then .111 would become .1, and if k = 2 it would become .11. We are interested in

$$P(d\in \tilde{D}|{\text{MAF}}^{\text{trunc}(k)}(\tilde{D})={\text{MAF}}^{\text{trunc}(k)}(D),d\in \tilde{B})$$

As above, we can calculate an upper bound, denoted by PrivMAF^trunc(k)(d, MAF^trunc(k)(D)). The approximation we use to calculate this is given in the Appendix. We then have

$${\text{PrivMAF}}^{\text{trunc}(k)}(D)=\underset{d\in D}{\text{max}}{\text{ PrivMAF}}^{\text{trunc}(k)}(d,{\text{MAF}}^{\text{trunc}(k)}(D))$$

For each d ∈ D, this measure upper bounds the probability that individual d participated in our study given only publicly-available data and knowledge of MAF^trunc(k)(D).

D. Measuring Privacy of Adding Noise

Another way to achieve privacy guarantees on released data is by perturbing the data using random noise (this is a common way of achieving differential privacy). Though there are many approaches to generate this noise, most famously by drawing it from the Laplace distribution [14], we investigate one standard approach to adding noise that is used to achieve differential privacy when releasing integer values [29].

Consider ε > 0. Let η be an integer valued random variable such that P(η = i) is proportional to e^−ε|i|. Let

$${\text{MAF}}_j^{\mathrm{\epsilon }}(D)={\text{MAF}}_j(D)+\frac{{\eta }_j}{2n}$$

where η₁, . . . , η_n are independently and identically distributed (iid) copies of η. It is worth noting that ${\text{MAF}}_j^{\in }(D)$ is 2ε-differentially private. Recall [14]:

Definition 1

Let n be an integer, Ω and Σ sets, and X a random function that maps n element subsets of Ω (we call such subsets ‘databases of size n‘) into Σ. We say that X is ε-differentially private if, for all databases D and D′ of size n that differ in exactly one element and all S ⊂ Σ, we have that

$$P(X(D)\in S)\le \mathit{\text{exp}}(\epsilon )P(X(D\prime )\in S)$$

Using the same framework as above we can define PrivMAF^ε (d, MAF^ε (D)) and PrivMAF^ε (D) to measure the amount of privacy lost by releasing MAF^ε (D). As above the approximation we use to calculate this is given in the Appendix.

E. Choosing the Size of the Background Population

One detail we did not go into above is the choice of N, where N is the number of people who could reasonably be assumed to have participated in the study. This parameter depends on the context, and giving a realistic estimate of it is critical. In most applications the background population from which the study is drawn is fairly obvious. That being said, one needs to be careful of any other information released publicly about participants–just listing a few facts about the participants can greatly reduce N, thus greatly reducing the bounds on privacy guarantees (since the amount of privacy lost by an individual is roughly inversely proportional to N − n, so doubling N gives us an estimate that is about half of what it would be otherwise).

Note that N can be considered as one of the main privacy parameters of our method. The smaller the N, the stronger the adversary we are protected against. Therefore we want to make N as large as possible, while at the same time ensuring the privacy we need. In our method, an adversary who has limited his pool of possible contenders to fewer than N individuals before we publish the MAF can be considered to have already achieved a privacy breach; thus it is a practitioner‘s job to choose N small enough that such a breach is unlikely.

F. Simulated Data

In what follows, all simulated genotype data was created by choosing a study size, denoted n, and a number of SNPs, denoted m. For each SNP a random number, p, in the range .05 to .5 was chosen uniformly at random to be the MAF in the background population. Using these MAFs we then generated the genotypes of n individuals independently. Note that all computations were run on a machine with 48GB RAM, 3.47GHz XEON X5690 CPU liquid cooled and overclocked to 4.4GHz, using a single core.

III. Results

A. Privacy and MAF

As a case study we tested PrivMAF on data from the Wellcome Trust Case Control Consortium (WTCCC)s 1958 British Birth Cohort [28]. This dataset consists of genotype data from 1500 British citizens born in 1958.

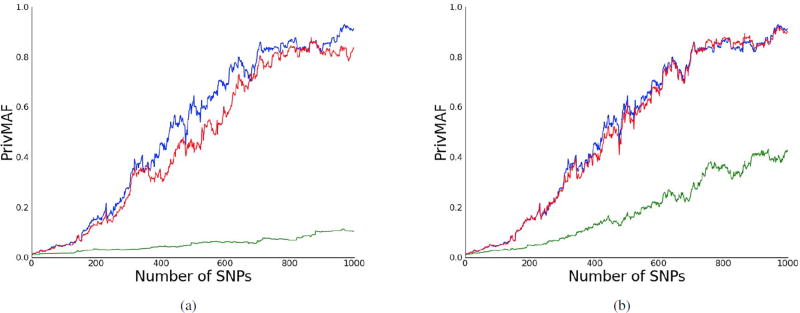
We first looked at the privacy guarantees given by PrivMAF for the WTCCC data for varying numbers of SNPs (blue curve, Fig. 1a), quantifying the relationship between number of SNPs released and privacy lost. The data were divided into two sets: one of size 1,000 used as the study participants, the other of size 500 which was used to estimate our model parameters (p_i’s). We assumed that participants were drawn from a background population of 100,000 individuals (N = 100, 000; see Methods for more details). Releasing the MAFs of a small number of SNPs results in very little loss of privacy. If we release 1,000 SNPs, however, we find that there exists a participant in our study who loses most of their privacy– based on only the MAF and public information we can conclude they participated in the study with 90% confidence.

Figure 1.

PrivMAF applied to the WTCCC dataset. In all plots we take n=1000 research subjects and a background population of size N=100,000. (a) Our privacy measure PrivMAF increases with the number of SNPs. The blue line corresponds to releasing MAFs with no rounding, the green line to releasing MAFs rounded to one decimal digit, and the red line to releasing MAFs rounded to two decimal digits. Rounding to two digits appears to add very little to privacy, whereas rounding to one digit achieves much greater privacy gains. (b) The blue line corresponds to releasing MAF with no noise, the red line to releasing MAF^.5, and the green line to releasing MAF^.1. Adding noise corresponding to ε = .5 seems to add very little to privacy, whereas taking ε = .1 achieves much greater privacy gains.

In addition, we considered the behavior of PrivMAF as the size of the population from which our sample was drawn increases. From the formula for our statistic we see that PrivMAF approaches 0 as the background population size, N, increases, since there are more possibilities for who could be in the study, while it goes to 1 as N decreases towards n.

B. Privacy and Truncation

Next we tested PrivMAF on perturbed WTCCC MAF data, showing that both adding noise and binning result in large increases in privacy. First we considered perturbing our data by binning. We bin by truncating the unperturbed MAFs, first to one decimal digit (MAF^trunc(1), k = 1) and then to two decimal digits (MAF^trunc(2), k = 2). As depicted in Fig. 1a we see that truncating to two digits gives us very little in terms of privacy guarantees, while truncating to one digit gives substantial gains.

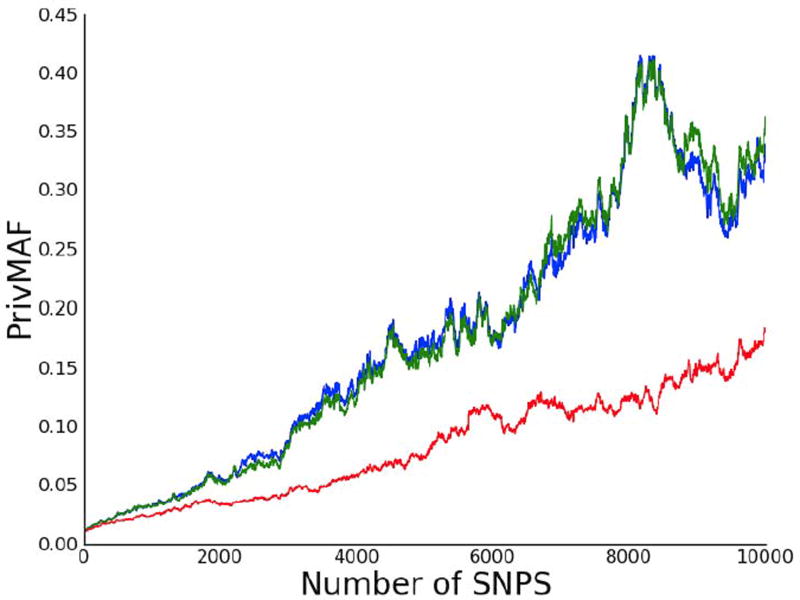
In practice, releasing the MAF truncated to one digit may render the data useless for most purposes. It seems reasonable to conjecture, however, that as the size of GWAS continues to increase similar gains can be made with less sacrifice. As a demonstration of how population size affects the privacy gained by truncation, we generated simulated data for 10,000 study participants and 10,000 SNPs, choosing N to be one million. We then ran a similar experiment to the one performed on truncated WTCCC data, except with k = 2 and k = 3; we found the k = 2 case had similar privacy guarantees to those seen in the k = 1 case on the real data (Fig. 2). For example, we see that if we consider releasing all 10000 SNPs then PrivMAF is near 0.35, while when k = 2 it is below 0.2 (almost a factor of two difference).

Figure 2.

Truncating simulated data to demonstrate scaling. We plot our privacy measure PrivMAF versus the number of SNPs for simulated data with n=10000 subjects and a background population of size N=1,000,000. The green line corresponds to releasing MAFs with no rounding, the blue line to releasing MAFs rounded to three decimal digit, and the red line to releasing MAFs rounded to two decimal digits. Rounding to three digits seems to add very little to privacy, whereas rounding to two digits achieves much greater privacy gains.

C. Privacy and Adding Noise

We also applied our method to data perturbed by adding noise to each SNPs MAF (Fig. 1b). We used ε = 0.1 and 0.5 as our noise perturbation parameters (see Methods). We see that when ε = 0.5, adding noise to our data resulted in very small privacy gains. When we change our privacy parameter to ε = 0.1, however, we see that the privacy gains are significant. For example, if we were to release 500 unperturbed SNPs then PrivMAF(D) would be over 0.4, while PrivMAF^.1(D) is still under 0.2.

The noise mechanism we use here gives us 2mε-differential privacy (see Methods), where m is the number of SNPs released. For ε = .1, if m = 200 then the result is 40-differentially private, which is a nearly useless privacy guarantee in most cases. Our measure, however, shows that the privacy gains are quite large in practice. This result suggests that PrivMAF allows one to use less noise to get reasonable levels of privacy, at the cost of having to make some reasonable assumptions about what information is publicly available.

Note that, using expected L₁ error as a measure of utility (unfortunately we are not aware of what alternative measures of utility might be most appropriate), we see that adding noise with parameter ε leads to an expected L₁ error of $\frac{1}{n(\mathit{\text{exp}}(\epsilon )-\mathit{\text{exp}}(-\epsilon ))}$. For ε = .5 this corresponds to an L₁ error of just under .001, while for ε = .1 this corresponds to an L₁ error of just under .005, both of which are relatively small.

D. Worst Case Versus Average

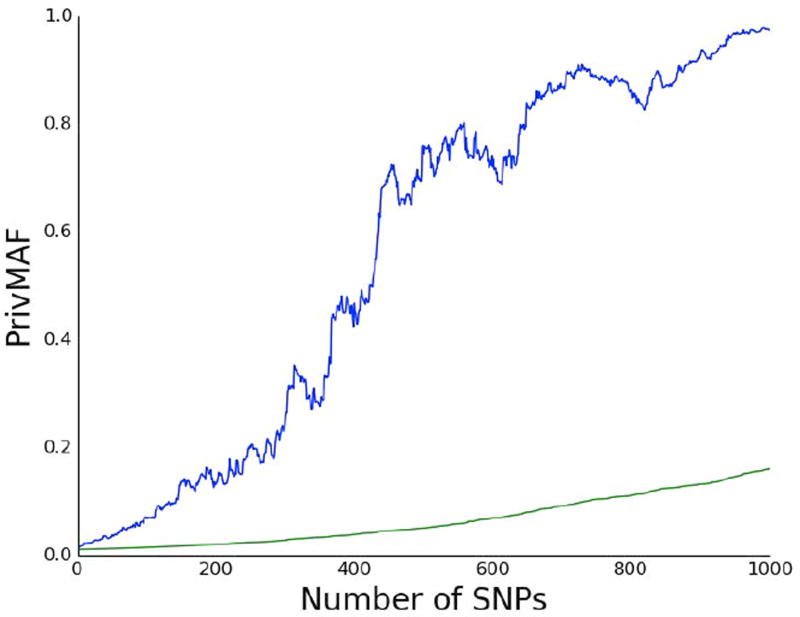
As stated earlier, the motivation for PrivMAF is that previous methods do not measure privacy for each individual in a study but instead provide a more aggregate measure of privacy loss. This observation led us to wonder exactly how much the privacy risk differs between individuals in a given study. To test this question, we compared the maximum and mean score of PrivMAF(d,MAF(D)) in the WTCCC example for varying values of m, the number of released SNPs. The result is pictured in Fig. 3. The difference is stark–the person with the largest loss of privacy (pictured in blue) loses much more privacy than the average participant (pictured in green). By the time m = 1000 the participant with the largest privacy loss is almost five times as likely to be in the study as the average participant. This result clearly illustrates why worse case, and not just average, privacy should be considered.

Figure 3.

Worst Case Versus Average Case PrivMAF. Graph of the number of SNPs, denoted m, versus PrivMAF. The blue curve is the maximum value of PrivMAF(d,MAF(D)) taken over all d ∈ D for a set of n = 1, 000 randomly chosen participants in the British Birth Cohort, while the green curve is the average value of PrivMAF(d,MAF(D)) in the same set. The the maximum value of PrivMAF far exceeds the average. By the time m = 1000 it is almost five times larger.

IV. CONCLUSION

On the one hand, to facilitate genomic research, many scientists would prefer to release even more data from studies [21], [31]. Though tempting, this approach can sacrifice study participants‘ privacy. As highlighted in the introduction, several different classes of methods have been previously employed to balance privacy with the utility of data. Methods such as sensitivity/PPV based methods are dataset specific, but only give average-case privacy guarantees. Because our method provides worst-case privacy guarantees for all individuals, we are able to ensure improved anonymity for individuals. Thus, PrivMAF can provide stronger privacy guarantees than sensitivity/PPV based methods. Moreover, since our method for deciding which SNPs to release takes into account the genotypes of individuals in our study, it allows us to release more data than any method based solely on MAFs with comparable privacy guarantees.

Our findings demonstrate that differential privacy may not always be the method of choice for preserving privacy of genomic data. Notably, perturbing the data appears to provide major gains in privacy, though these gains come at the cost of utility. That said, our results suggest that, when n is large, truncating minor allele frequencies may result in privacy guarantees without the loss of too much utility. Moreover, the method of binning we used here is very simple– it might be worth considering how other methods of binning may be able to achieve similar privacy guarantees while resulting in less perturbation on average. We further show that adding noise can result in improved privacy, even if the amount of noise we add does not provide reasonable levels of differential privacy.

Note that our method is based off a certain model of how the data is generated, a model that is similar to those used in previous approaches. It will not protect against an adversary that has access to insider information. This caveat, however, seems to be unavoidable if we do not want to turn to differential privacy or similar approaches that perturb the data to a greater extent to get privacy guarantees, thus greatly limiting data utility. It would be of interest to develop methods for generalizing this model based approach to other types of aggregate genomic data (p-values, multiple different statistics, etc), though it is not obvious how to do so.

These assumptions lead some to wonder about model misspecification. For example, if we assume when calculating PrivMAF that the underlying population is of British ancestry then our model does not give privacy guarantees for an individual in the study not of British ancestry. In practice this should lead to overestimation of privacy risk to that individual, since (with high probability) the likelihood of that individual‘s genome having been produced under a model derived from individuals of British ancestry is much lower than it would be under a correct probability model. As such we are likely to overestimate the probability of that individual being in our cohort. Despite this caveat, in order to ensure privacy practitioners should check that the assumptions we make are reasonable in their study.

Having presented results on moderate-sized real datasets, we test the ability of PrivMAF to scale as genomic data sets grow. In particular, we ran our algorithm on larger artificial datasets (with 10,000 individuals and 1000 SNPs) and have found our PrivMAF implementation still runs in a short amount of time (19.14 seconds on our artificial dataset of size 10,000 described above, with a running time of O(mn), where n is the study size and m is the number of SNPs).

Though our work focuses on the technical aspects related to preserving privacy, a related and equally important aspect comes from the policy side. Methods similar to those presented here offer the biomedical community the tools it needs to ensure privacy; however, the community must determine appropriate privacy protections (ranging from the release of all MAF data to use of controlled access repositories) and in what contexts (i.e., do studies of certain populations, such as children, require extra protection?). It is our hope that our work helps inform this debate. Our tool could, for example, be used in combination with controlled access repositories to release the MAFs of a limited number of SNPs depending on what privacy protections are deemed reasonable

Our work addresses the critical need to provide privacy guarantees to study participants and patients by introducing a quantitative measurement of privacy lost by release of aggregate data, and thus may encourage release of genomic data.

A Python implementation of our method, as well as more detailed derivations of our results, are available at http://privmaf.csail.mit.edu.

Appendix

A. Derivation of PrivMAF

We give a quick sketch of the derivation for PrivMAF on unperturbed data, the derivation for the perturbed versions being similar. A more detailed derivation is available at http://privmaf.csail.mit.edu. Note that we use the notation D̃ = {z̃₁, · · ·, z̃_n}.

We begin with Pr(d ∈ D̃|d ∈ B̃, MAF(D̃) = MAF(D)). Let P_n and x(D) be as in Section II-B. By repeated us of Bayes law, the fact

$$P_{n-1}(x(D)-d)=\text{Pr}(x(\tilde{D})=x(D)|d_1=d)$$

and the fact that B̃ − D̃ = {b ∈ B̃|b ∉ D̃ and D̃ are independent random variables, we get that this equals

$$\frac{1}{1+\left(\frac{\text{Pr}(d\in \tilde{B}-\tilde{D}}{1-{(1-\text{Pr}(d={\tilde{z}}_1)\frac{P_{n-1}(x-d)}{P_n(x)})}^n}\right)-\text{Pr}(d\in \tilde{B}-\tilde{D})}$$

Using the fact that (1 − z)ⁿ ≥ 1 − nz when 0 ≤ z ≤ 1 (this follows from the inclusion exclusion principle) we get that this is

$$\le \frac{1}{1-\text{Pr}(d\in \tilde{B}-\tilde{D})+\frac{\text{Pr}(d\in \tilde{B}-\tilde{D})(P_n(x))}{n\text{ Pr}(d={\tilde{z}}_1)P_{n-1}(x-d)}}$$

Note that for realistic choices of n, N, p and m we get that Pr(d ∈ B̃ − D̃) is approximately equal to (N − n) Pr(d = z̃₁) and that Pr(d ∈ B̃ − D̃) << 1, so 1 − Pr(d ∈ B̃ − D̃) ≈ 1. Plugging this in we get the measure

$$\text{PrivMAF}(d,\text{MAF}(D))\approx \frac{1}{1+\frac{(N-n)P_n(x)}{n{P}_{n-1}(x-d)}}$$

which is what we use in practice.

B. Perturbed Statistics

When calculating PrivMAF^ε we use the approximation

$${\text{PrivMAF}}^{\epsilon }(d,{\text{MAF}}^{\epsilon }(D))\approx \frac{1}{1+\frac{(N-n)P_n^{\epsilon }({\text{MAF}}^{\epsilon }(D))}{n{P}_{n-1}^{\epsilon }({\text{MAF}}^{\epsilon }(D)-d)}}$$

where

$$P_n^{\epsilon }(v)=\prod _{j=1}^m\sum _{i=0}^{2n}\left(\begin{array}{c}2n\hfill \\ i\hfill \end{array}\right)p_j^i{(1-p_j)}^{2n-i}\text{Pr}(\eta =2n{v}_j-i)$$

Similarly, when considering truncated data, we use the approximation

$${\text{PrivMAF}}^{\text{trunc}(k)}(d,{\text{MAF}}^{\text{trunc}(k)}(D))\approx \frac{1}{1+\frac{N-n}{n}\frac{\text{Pr}({\text{MAF}}^{\text{trunc}(k)}(\tilde{D})=v)}{\text{Pr}({\text{MAF}}^{\text{trunc}(k)}(\tilde{D})=v|d={\tilde{z}}_1)}}$$

where

$$\text{Pr}({\text{MAF}}^{\text{trunc}(k)}(\tilde{D})=v)=\prod _{j=1}^m\text{Pr}({\text{MAF}}_j^{\text{trunc}(k)}(\tilde{D})=v_j)$$

and

$$\text{Pr}({\text{MAF}}^{\text{trunc}(k)}(\tilde{D})=v|d={\tilde{z}}_1)=\prod _{j=1}^m\text{Pr}({\text{MAF}}_j^{\text{trunc}(k)}(\tilde{D})=v_j|d={\tilde{z}}_1)$$

Letting $S_k(v_j)=\left\{x\right|\frac{x}{2n}\text{truncates to }{v}_j\}$, we see that

$$\text{Pr}({\text{MAF}}_j^{\text{trunc}(k)}(\tilde{D})=v_j)=\sum _{i\in S_k(v_j)}\left(\begin{array}{c}2n\hfill \\ i\hfill \end{array}\right)p_j^i{(1-p_j)}^{2n-i}$$

and

$$\text{Pr}({\text{MAF}}_j^{\text{trunc}(k)}(\tilde{D})=v_j|d={\tilde{z}}_1)=\sum _{i\in S_k(v_j)}(\begin{array}{c}2n-2\hfill \\ i-d_j\hfill \end{array})p_j^i{(1-p_j)}^{2n-i+d_j-2}$$

This allows us to calculate ${\text{PrivMAF}}^{\text{trunc}(k)}(d,{\text{MAF}}_j^{\text{trunc}(k)}(D))$, just as we wanted. The exact formulas and the corresponding derivations for PrivMAF^trunc(k) and PrivMAF^ε are available at http://privmaf.csail.mit.edu.

C. Changing the Assumptions

The above model makes a few assumptions (assumptions that are present in most previous work that we are aware of). In particular it assumes that there is no linkage disequilibrium (LD) (which is to say that the SNPs are independently sampled), that the genotypes of individuals are independent of one another (that there are no relatives, population stratification, etc. in the population), and that the background population is in Hardy-Weinberg Equilibrium (H-W Equilibrium). The assumption that genotypes of different individuals are independent from one another is difficult to remove, and we do not consider it here. We can, however, remove either the assumption of H-W Equilibrium or of SNPs being independent.

First consider the case of H-W Equilibrium. Let us consider the ith SNP, and let p_i be the minor allele frequency. We also let p_0,i, p_1,i and p_2,i be the probability of us having zero, one, or two copies of the minor allele respectively. Assuming the population is in H-W equilibrium is the same as assuming that p_0,i = (1 − p_i)², p_1,i = 2p_i(1 − p_i), and $p_{2,i}=p_i^2$. Dropping this assumption, we see that all of the calculations above still hold, except we get that

$$\text{Pr}(x_i(\tilde{D})=x_i)=\sum _{c=0}^{\lfloor \frac{x_i}{2}\rfloor }\left(\begin{array}{c}n\hfill \\ c\hfill \end{array}\right)\left(\begin{array}{c}n-c\hfill \\ x_i-2c\hfill \end{array}\right)p_{0,i}^{n-x_i+c}{p}_{1,i}^{x_i-2c}{p}_{2,i}^c$$

where we use the convention that $\left(\begin{array}{c}n\hfill \\ c\hfill \end{array}\right)=0$ when c < 0. This allows us to remove the assumption of H-W Equilibrium. Unfortunately there are two problems with this approach. The first is statistical– instead of having to just estimate one parameter per SNP (p_i), we have to estimate two (p_0,i and p_1,i, since p_2,i can be calculated from the other two). The other problem is that calculating Pr(x_i(D) = x_i) suddenly becomes more computationally intensive, so much so that it is prohibitive for large data sets.

In order to allow us to drop the assumption of no LD we can model the genome as a Markov model (you could also use a hidden Markov model instead which allows for more complex relationships, but for simplicity sake we will only talk about Markov models since the generalization to HMM is straightforward). In such a model the state of a given SNP only depends on the state of the previous SNP. To specify such a model we need to specify the probability distribution of the first SNP, and for each subsequent SNP we need to specify its distribution conditional on the previous SNP. It is then straightforward to modify our framework to deal with this model. As above, however, this requires us to estimate lots of parameters and also is much more time consuming; thus it is not likely to be useful in practice.

Finally, we assume that D is chosen uniformly at random from B. This can be thought of as assuming that the adversary has no knowledge about how the genomic make up of D differs from that of B. If this is not the case then different probabilistic models may have to be used. In particular, we would like to develop probabilistic models that take into account the release of other aggregate data (such as regression coefficients, p-values, etc)– such models will likely require us to abandon the assumption of individuals being chosen uniformly at random.

It is worth noting that choosing a smaller N could conceivably be used as a buffer to help protect against such misspecification. More specifically, the adversary has a prior belief Pr(d ∈ D| background knowledge). In our model we assume that this equals $\text{Pr}(d\in D|d\in B)\approx \frac{n}{N}$ (where there are some complications due to the possibility of duplicate genomes). This gives us a correspondence between the choice of N and the choice of Pr(d ∈ D| background knowledge), so choosing smaller N could help overcome this issue. The exact way in which N determines our privacy measure can be seen in Fig S5 on our website at http://privmaf.csail.mit.edu.

D. Release Mechanism

Often one might like to use PrivMAF to decide if it is safe to release a set of MAF from a study. This can be done by choosing α between 0 and 1 and releasing the MAF if and only if PrivMAF(D) ≤ α. The action of deciding to release D or not release D, however, gives away a little information. In practice this is unlikely to be an issue, but in theory it can lead to privacy breaches. This issue can be dealt with by releasing the MAF if and only if PrivMAF(D) ≤ β(α), where β = β(α) is chosen so that:

$$\alpha \ge \frac{1}{1+\frac{P_{\beta }}{\beta }-P_{\beta }-{\text{max}}_{d\in \{0,1,2\}m}\text{Pr}(d\in \tilde{B}-\tilde{D})}$$

where

$$P_{\beta }=\text{Pr}(\underset{d\in \tilde{D}}{\text{max}}\text{ PrivMAF}(d,\text{MAF}(\tilde{D}))\le \beta |x(\tilde{D})=x)$$

We call this release mechanism the Allele Leakage Guarantee Test (ALGT). Unlike the naive release mechanism ALGT gives us the following privacy guarantee:

Theorem 1

Choose β as above. Then, if PrivMAF(D) ≤ β, for any choice of d ∈ D we get that

$$P(d\in \tilde{D}|d\in \tilde{B},x(\tilde{D})=x,(\underset{\tilde{d}\in \tilde{D}}{\text{max}}\mathit{\text{ PrivMAF}}(\tilde{d},\mathit{\text{MAF}}(\tilde{D}))\le \beta )$$

is less than or equal to α.

Note that the choice of α determines the level of privacy achieved. Picking this level is left to the practitioner– perhaps an approach similar to that taken by Hsu et al. [30] is appropriate.

A more detailed proof of the privacy result above can be found at http://privmaf.csail.mit.edu.