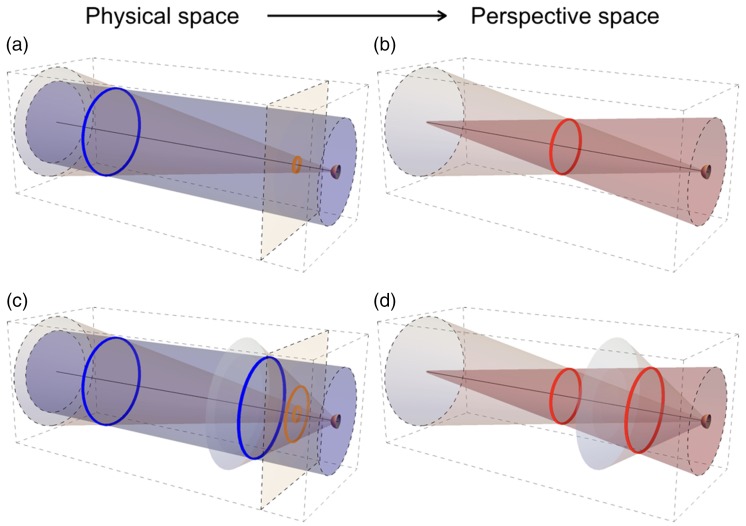
Figure 1.

Sizes and distances of rings in physical and perspective space. (a) One ring in physical space. The observer (half sphere at the right side) fixates the center of the ring (blue). The black line indicates the (binocular or monocular) viewing direction. The ring defines a set of directions (forming the cone with its vertex at the observer). The ring also defines a set of lines parallel to the viewing direction, indicating physical trajectories if the ring would move in the viewing direction. The parallel lines together form a cylinder, projecting a circle the size of the ring in the plane of the observer. The orange plane orthogonal to the viewing direction contains the projection (orange) of the ring on a two-dimensional planar surface. (b) The ring of (a) in perspective space. The directional cone is identical to that in physical space. The parallels in physical space are converted to lines converging to a vanishing point in perspective space, indicating trajectories if the ring would move in the viewing direction. Together, the converging lines form a cone having its vertex at the vanishing point. Intersection between the two cones forms the ring (red) in perspective space. (c) Two identical rings at different distances in physical space. The two rings (blue) project to two concentric rings (orange) in the picture plane, indicating their relative size on the retina. (d) The two rings of (c) in perspective space. Size ratio of the rings (red) depends on the distance of the vanishing point and lies in between size ratios in the picture plane (orange) and physical space (blue) for positive finite vanishing distances.