Abstract
Expression quantitative trait loci (eQTL) studies have typically used single-variant association analysis to identify genetic variants correlated with gene expression. However, this approach has several drawbacks: causal variants cannot be distinguished from nonfunctional variants in strong linkage disequilibrium, combined effects from multiple causal variants cannot be captured, and low-frequency (<5% MAF) eQTL variants are difficult to identify. While these issues possibly could be overcome by using sparse polygenic models, which associate multiple genetic variants with gene expression simultaneously, the predictive performance of these models for eQTL studies has not been evaluated. Here, we assessed the ability of three sparse polygenic models (Lasso, Elastic Net, and BSLMM) to identify causal variants, and compared their efficacy to single-variant association analysis and a fine-mapping model. Using simulated data, we determined that, while these methods performed similarly when there was one causal SNP present at a gene, BSLMM substantially outperformed single-variant association analysis for prioritizing causal eQTL variants when multiple causal eQTL variants were present (1.6- to 5.2-fold higher recall at 20% precision), and identified up to 2.3-fold more low frequency variants as the top eQTL SNP. Analysis of real RNA-seq and whole-genome sequencing data of 131 iPSC samples showed that the eQTL SNPs identified by BSLMM had a higher functional enrichment in DHS sites and were more often low-frequency than those identified with single-variant association analysis. Our study showed that BSLMM is a more effective approach than single-variant association analysis for prioritizing multiple causal eQTL variants at a single gene.
Keywords: eQTLs, causal variants, sparse polygenic models
RECENT studies (Lappalainen et al. 2013; Battle et al. 2014; The GTEx Consortium 2015) have investigated associations between gene expression and genetic variants [expression quantitative trait loci (eQTLs)] by analyzing tissue samples from hundreds of individuals. Through these efforts, tens of thousands of eQTLs, some of which are tissue-specific, have been associated with gene expression, largely via single-variant association analysis in which multiple SNPs are tested per gene independently, the most significantly associated SNP is identified, and a permutation-adjusted P-value is used to control overall false discovery rate (FDR) (The GTEx Consortium 2015). However, there are several drawbacks to this approach: (1) noncausal eQTL variants can show the strongest association at a gene due to linkage disequilibrium (LD); (2) combined effects from multiple causal eQTL variants cannot be estimated, which is not ideal when two or more regulatory variants jointly affect gene expression (Tao et al. 2006; Corradin et al. 2014); and (3) common variants tend to have higher P-values than lower-frequency variants of equal effect size (Wakefield 2009). As rare noncoding variants can contribute to individual gene expression levels (Li et al. 2014), and are more likely to be deleterious than common variants (1000 Genomes Project Consortium et al. 2012), it is important to be able to identify rare causal eQTL variants. Thus, a robust approach for identifying causal eQTL variants that overcomes these drawbacks of single-variant association analysis is desirable.
Previous studies have attempted to overcome the limitations of single-variant association analysis through the application of fine-mapping methods (Servin and Stephens 2007; Hormozdiari et al. 2014; Kichaev et al. 2014). Although these approaches have been shown to be more effective than single-variant association analysis, they have two major drawbacks: (1) they are computationally intensive as each combination of variants must be tested for causality separately, and, hence, to limit the number of variants examined at a locus, the 100 highest ranked variants from a single-variant association analysis are typically used as input (Chiang et al. 2017); and (2) the number of causal eQTL variants at a locus must be specified as a parameter a priori, which results in the analysis being biased toward a defined number of causal eQTL variants.
Recently, sparse polygenic modeling approaches, which assume only a small fraction of genetic variants are causal for altering gene expression levels, have been shown to have higher power and better predictive performance over single-variant association analysis in yeast eQTL studies (Lee et al. 2009; Cheng et al. 2016); however, their ability to identify human eQTLs has yet to be studied in depth. Several of these models' properties suggest that they may better prioritize causal eQTL variants than single-variant association analysis in human studies, the most important of which is their ability to estimate the effect sizes of variants jointly, rather than independently, thereby taking LD structure into account as a correlation between variables. This joint modeling suggests they possibly could identify multiple causal eQTL variants per gene, and discriminate functional variants from nonfunctional variants in LD. Furthermore, as some of these models learn the number of causal eQTL variants from the data, rather than using an a priori specified parameter, more low-frequency variants possibly could be identified.
In this paper, we compared three sparse polygenic models for eQTL SNP discovery—Lasso (Tibshirani 1996), Elastic Net (Zou and Hastie 2005), and BSLMM (Zhou et al. 2013)—to the BIMBAM fine mapping method (Servin and Stephens 2007) and single-variant association analysis. Through simulated analysis with varying scenarios, we found that BSLMM consistently outperformed all other methods at prioritizing multiple causal eQTL variants. We also applied all three sparse polygenic models to RNA-seq and whole-genome sequencing (WGS) data of 131 induced pluripotent stem cell (iPSC) samples, and observed that variants prioritized by BSLMM were more likely causal as they were highly enriched in iPSC DNase I hypersensitive sites (DHSs); more deleterious on average; more likely to be low-frequency [minor allele frequencies (MAF) <5%]; and often plausibly regulatory as they were located in functional elements. Finally, we compared the efficacy of BSLMM and single-variant association analysis across the same metrics using SNP array data, and found that BSLMM outperformed single-variant association analysis for genes with multiple independent eQTL SNPs. Overall, our results show that BSLMM outperforms single-variant association analysis at prioritizing low frequency variants, likely regulatory variants, and multiple causal eQTL variants at the same gene.
Materials and Methods
Linear additive model of gene expression
In our simulation data analysis, we assume a simple linear additive model for gene expression
| (1) |
where = {yn} is an N × 1 vector of gene expression data, N is the sample size, X = {xnm} is an N × M genotype matrix normalized with mean zero and variance 1, b = {} is an M × 1 vector of per-normalized-genotype effect size, M is the number of causal eQTL variants, and e = {en} is an N × 1 vector of random noise. For simplicity, we assume that per-normalized-genotype effect sizes for variants are drawn from the distribution
| (2) |
where (the narrow-sense heritability) is formally defined as the ratio of expectation of the proportion of phenotypic variances explained by genotypes, as previously described (Guan and Stephens 2011). We also assume that X, b, and e are mutually independent. Since columns of X are normalized with mean and variance 1, the expected value of can be calculated as
and random noise is drawn from the distribution (3)
| (4) |
Under this polygenic model, where genotypes are normalized to mean zero and variance 1, effect sizes are drawn independently from distributions with variance proportional to where f is the MAF of the variants with the assumption that rarer variants tend to have larger effect sizes than common variants (Bulik-Sullivan et al. 2015).
Simulated data generation
We extracted biallelic single nucleotide polymorphisms (SNPs) with MAF >1.0% segregating in the European population (503 individuals) in the 1000 Genomes Projects Phase 3 data (Auton et al. 2015), following which a Hardy-Weinberg Equilibrium test was conducted and SNPs with P-values ≤1.0 × 10−5 were filtered out. For each simulation, we selected the number of causal variants per gene (1, 2, 5, or 10), the narrow-sense heritability for each gene (20% or 60%), and assumed that “true” causal eQTL variants were located within 1 Mb of the gene’s transcription start site (TSS). Within each simulation, for each gene, SNP positions were randomly chosen so that the distance from TSS to the causal eQTL variants followed an empirical distribution constructed from a previous large-scale eQTL study (Lappalainen et al. 2013), SNP effect sizes were drawn independently from the distribution described by Equation (2) such that per-normalized-genotype effect size was proportionally distributed across causal eQTL variants for each gene, and gene expression level was generated from Equation (1).
Whole-genome sequence and RNA-seq data of iPSC samples
WGS data of 215 individuals in the iPSCORE (iPSC Collection for Omic Research) cohort (Panopoulos et al. 2017), and RNA-seq data of the iPSC samples generated from the corresponding individuals (DeBoever et al. 2017), were obtained. All samples from the iPSCORE resource were obtained from consented individuals under the approval of the Institutional Review Boards of the University of California, San Diego. The reads from WGS were aligned to human genome hg19 with decoy sequences using BWA-MEM (Li and Durbin 2009) as previously described (DeBoever et al. 2017). Briefly, duplicate reads were marked in BAM format, variant calling was performed using HaplotypeCaller, and the genotyping quality of SNVs and indels were assessed using the Variant Quality Score Recalibration (VQSR) approach implemented in GATK (Van der Auwera et al. 2013).
Transcripts per million (TPM) were estimated with RSEM (Li et al. 2010) from RNA-seq data of each sample, followed by quantile normalization using normalize.quantiles in the preprocessCore R package. Then, for each gene, the expression values were rank normalized to mean zero and variance one. Finally, the top 15 PEER factors were regressed out from the expression values, and the remaining residuals were used for the eQTL analysis.
From the obtained genotypes of the 215 individuals, the kinship coefficients were calculated by EPACTS (http://csg.sph.umich.edu/kang/epacts/), and 131 unrelated individuals were selected such that the kinship coefficients were <0.05 for all pairs of individuals. We conducted a Hardy-Weinberg Equilibrium test and obtained 10,111,635 biallelic SNPs with P-value ≤1.0 × 10−5 and MAF >1% with VCFtools (version 0.1.14) (Danecek et al. 2011), which were used for eQTL SNP discovery.
eQTL discovery from gene expression and genotype data
We obtained 17,819 expressed autosomal genes, in which ≥10 samples have TPM >1. Then, we extracted all the biallelic SNPs located ±1 Mb surrounding the transcription start site (TSS), which resulted in 6215 SNPs per gene on average. For single-variant association analysis, FastQTL (Ongen et al. 2016) version 2.184 was used to obtain the significance values for each eQTL SNP per gene at FDR <5%. First, nominal P-values were calculated with linear regressions between sample genotypes at each SNP and expression level, and then corrected P-values were obtained for the most significant eQTL SNPs by performing 1000 permutations followed by β approximations (Ongen et al. 2016). Then, from the set of all permutation P-values, FDR was calculated to determine significant eQTL SNPs by Benjamini and Hochberg correction.
For sparse polygenic modeling approaches with Elastic Net and Lasso, genotypes were coded in 0, 1, or 2, after missing genotypes in VCF format were converted to reference alleles. Then, for each SNP site, coded genotypes of individuals were normalized to mean zero and variance one. We assumed a simple linear additive model for gene expression as in (1), and the R package glmnet (Friedman et al. 2010) was used to apply Lasso and Elastic Net for variable selection and joint estimation of effect sizes. The tuning parameter lambda was estimated by 10-fold cross validation for each gene, as implemented in glmnet. As a result, per-normalized-genotype effect sizes for variants were estimated and used in our analysis. The assumptions underlying the degree of polygenicity for gene expression is another parameter that may affect prediction performance with sparse polygenic modeling approaches. In Elastic Net, the mixing parameter controls polygenicity, ranging from a small number of variants when is close to one (the algorithm performs like Lasso), to all the variants when is close to zero (the algorithm performs like Ridge), and can be set somewhere in between () (Zou and Hastie 2005). For Elastic Net, we use in our data analyses, assuming that, for most genes, the number of cis-regulatory variants affecting gene expression is sparse, as previously suggested (Wheeler et al. 2016). For both Lasso and Elastic Net, we ranked SNPs by the absolute values of their effect sizes.
For the sparse polygenic modeling approach BSLMM, GEMMA software (http://www.xzlab.org/software/gemma-0.94.1/gemma) was used (Zhou et al. 2013) to obtain the posterior mean estimate of effect size. BSLMM assumes a linear mixed model with a random effect term:
| (5) |
where = {yn} is an N × 1 vector of gene expression data, N is the sample size, ={1} is an N × 1 vector of 1 s, is a scalar representing mean, X = {xnm} is an N × M genotype matrix (coded as 0, 1, or 2, and then centered with mean zero), M is the number of variants, is an M × 1 vector of sparse effect size, is an N × 1 vector of random effects, is an N × N kinship matrix, e = {en} is an N × 1 vector of random noise, and are unknown hyper-parameters. The main difference between the generic mixed model (5) and the generic linear model (1) is the additional random effect term which captures the combined small effects of all markers, and, as it is modeled as a multivariate-normal distribution, includes a covariance term for each pair of samples. BSLMM assumes that a few SNPs have large effect sizes, and that the other SNPs have small effect sizes, to simultaneously estimate the effect sizes of all cis-SNPs by estimating the posterior distribution of each parameter with the MCMC algorithm based on a sparse regression model (5). It is important to note that the use of the MCMC algorithm can produce uneven estimation of effect sizes for variants in extreme LD, which results in a somewhat random prioritization of such variants. After applying BSLMM, the associated variants were ranked by absolute values of the posterior mean of the estimated effect sizes.
For Bayesian fine-mapping, we utilized BIMBAM version 1.0 (http://www.haplotype.org/bimbam.html). To measure the evidence for genetic association, a Bayes factor (BF) was calculated for each variant by finding the likelihood ratio of H1 (variant is causal) to H0 (variant is not causal) (Servin and Stephens 2007). Given a prior distribution on the number of causal eQTL variants, where is the number of causal variants, the BF of a particular SNP being causal is calculated as:
where is the maximum number of causal eQTL variants (to keep computation feasible, we used five), is the total number of cis-eQTL SNPs [to keep computation feasible, we used the 100 highest ranked eQTL SNPs from single-variant association analysis, as conducted previously (Chiang et al. 2017)], and denotes the ensemble of all possible combinations of SNPs. We ranked the eQTL SNPs based on their BF in descending order.
Computational time for eQTL analysis with sparse polygenic models
BSLMM required 959 sec (16 min), whereas single-variant association analysis (FastQTL), Elastic Net, and Lasso, required 4, 17, and 18 sec, respectively, on average per gene on a computer with an Intel E5-2640 processor (2.60 GHz) with the CentOS release 6.6. Since BSLMM uses the Markov Chain Monte Carlo (MCMC) algorithm to estimate the posterior distributions of parameters, it gains prediction accuracy at the cost of computational time.
Annotation of DHSs and ChIP-seq peaks
We downloaded the narrow peak bed files of DHSs, H3K4me3, H3K4me1, and H3K27ac ChIP-seq data of Homo sapiens iPS DF 6.9 induced pluripotent stem cell line male newborn (Roadmap Epigenomics et al. 2015) from the Roadmap Epigenomics Mapping Consortium web portal (http://egg2.wustl.edu/roadmap/web_portal/processed_data.html). We downloaded the narrow peak bed files of OCT4 and NANOG ChIP-seq data of Homo sapiens H1-hESC stem cell male embryo from the ENCODE Project website (https://www.encodeproject.org/) (accession numbers ENCFF002CJF and ENCFF002CJA, respectively).
Functional analysis of eQTL SNPs
To determine the enrichment of eQTL SNPs within DHSs, we determined background frequency as follows: (1) we obtained 3442 eQTL SNPs from single-variant association analysis with FastQTL at 5% FDR; (2) for each eQTL SNP, we extracted the surrounding 5 kb genomic region (±2.5 kb) excluding ±100 bp immediately surrounding the SNP position; and (3) we measured the frequency of DHSs within these genomic regions. To assess the deleteriousness of eQTL SNPs, we downloaded Combined Annotation Dependent Depletion (CADD) scores of all SNPs in GRCh37/hg19 from (http://cadd.gs.washington.edu/download).
Genotype imputation
To simulate Illumina Omni2.5 genotyping array (ftp://ftp.illumina.com/Downloads/ProductFiles/HumanOmni25/v1-1/HumanOmni2-5-8-v1-1-C.csv) data, we extracted the genotypes at the corresponding SNP sites from the iPSCORE WGS data. In total, 1,616,286 biallelic SNP sites were extracted out of 10,111,635 biallelic SNP sites discovered from the whole genome sequence data. From the extracted genotypes, genotypes were imputed with IMPUTE2 (Howie et al. 2009) using the 1000 Genomes Phase 3 reference panel (Auton et al. 2015). Imputed variants with an INFO score >0.4 were retained, and variants deviating from Hardy-Weinberg equilibrium (P-value ≤1.0 × 10−5) were filtered out.
Data availability
All simulated data are available by request to the corresponding author. Genotype calls from the whole genome sequence data are available through NCBI dbGaP: phs001325.v1.p1. The RNA sequencing data are available through dbGaP: phs000924.v1.p1.
Results
Generation of simulated data for input to eQTL analyses
To investigate the ability of sparse polygenic modeling approaches to identify causal eQTL variants, we simulated gene expression data for hypothetical samples under a simple linear model, based on real genotypes from the European population in the 1000 Genomes Projects Phase 3 data (Auton et al. 2015). We simulated expression data with a combination of various parameters including the number of causal eQTL variants per gene (1, 2, 5, or 10), the number of samples (503 or 100), and narrow-sense heritability of gene expression data (20% or 60%). These simulated expression levels and their corresponding SNPs were used as input data for association analyses performed with the three sparse polygenic models and the single-variant association analysis; however, due to computational constraints for BIMBAM, the highest 100 ranked SNPs by single-variant association analysis at each gene were used as input.
Performance metrics of eQTL discovery
To assess the ability of each model to accurately identify causal eQTL variants, we calculated the precision-recall (PR) curves using the simulated datasets. To identify positively associated eQTL SNPs, we ranked the eQTL SNPs identified by each method as follows, and selected the N highest ranked SNPs: we ranked single-variant association analysis eQTL SNPs by statistical significance (P-values) and effect size, Elastic Net and Lasso eQTL SNPs by the absolute values of estimated effect sizes, BSLMM eQTL SNPs by the absolute values of posterior mean of effect size, and BIMBAM eQTL SNPs by BF. For all simulated data sets, including those with multiple causal eQTL variants per gene, we define precision as the fraction of identified eQTL SNPs that are truly causal, and recall as the fraction of truly causal eQTL variants that are identified. For example, if we simulate two truly causal eQTL SNPs per gene, and use the 20 highest ranked SNPs (N = 20), there are a total of 2000 true eQTL SNPs across the 1000 genes, and a total of 20,000 eQTL SNPs; therefore, if we identify 1500 of the 2000 true eQTL SNPs, our precision is 0.075 (1500/20,000) and recall is 0.75 (1500/2000).
To determine the range of the PR parameter to use in our analyses (i.e., the number of N highest ranked eQTL SNPs considered as positive associations), we measured the ability of each model to identify at least one causal eQTL variant at a gene when we simulated either 1, 2, 3, or 10 causal eQTL variants at each gene (Supplemental Material, Figure S1 in File S1). We noted that, for all numbers of simulated causal eQTL variants, the curves plateaued at ∼20, indicating that considering more than the 20 highest ranked eQTL SNPs would result in a large loss of precision and only a small gain in recall. We therefore parameterized the PR curves from the highest ranked eQTL SNP (the top eQTL SNP), to the 20 highest ranked eQTL SNPs at each of the 1000 genes.
Comparing the performance of sparse polygenic models to that of fine-mapping and single-variant association analysis
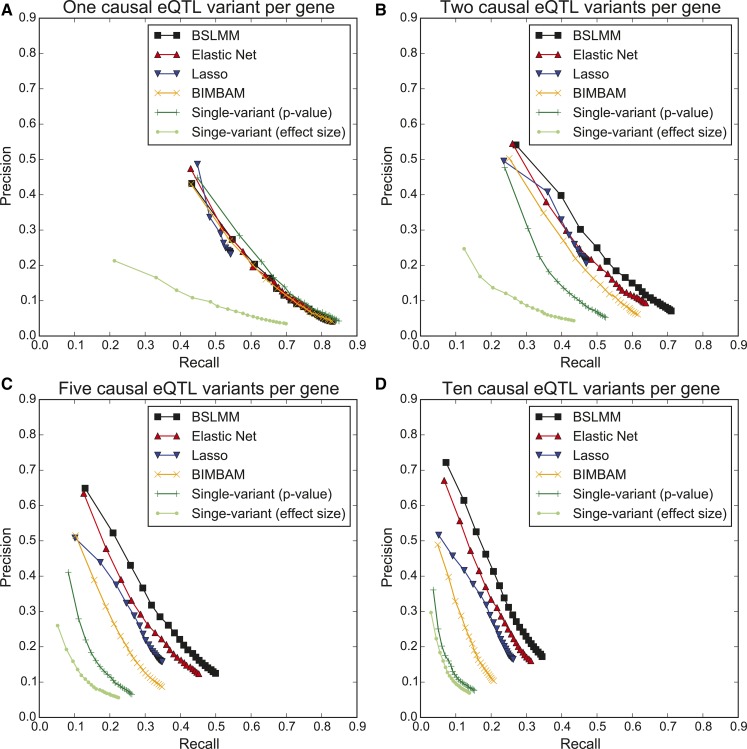
To determine the ability of each association analysis to identify causal eQTL variants, we initially measured the precision and recall of each method on 503 simulated samples with 60% gene expression heritability and either 1, 2, 5, or 10 causal eQTL variant(s) per gene. We examined the PR curves for single-variant association analysis eQTL SNPs ranked by either effect size or P-value, and observed a consistently higher recall rate when ranking by P-value (Figure 1); we therefore only compared the single-variant association analysis P-value ranked eQTL SNPs with the sparse polygenic models and BIMBAM.
Figure 1.
Prediction performance for identifying causal eQTL variants from simulation data of 503 samples with 60% heritability. PR curves parametrized by the number of highest ranked eQTL SNPs (ranging from 1 to 20) at 1000 randomly selected genes. (A) One causal eQTL variant per gene. (B) Two causal eQTL variants per gene. (C) Five causal eQTL variants per gene. (D) Ten causal eQTL variants per gene.
We examined precision when only the top eQTL SNP was considered: all models had precision of ∼50% (range:43–49%; Figure 1A), likely due to noncausal variants in LD with the causal variant showing association signals of similar strength, a common problem in GWAS (Malo et al. 2008). We then examined the PR curves of each method with a single simulated casual eQTL variant, considering the 20 highest ranked eQTL SNPs per gene. BSLMM, BIMBAM, and single-variant association analysis identified ∼83% of the causal eQTL variants across the 1000 genes; however, Elastic Net and Lasso performed less well with 76% and 54% recall, respectively (Figure 1A), likely due to the two models conducting shrinkage, thereby identifying a small subset of eQTL SNPs at each gene on average (Elastic Net:16.3; Lasso:2.3) (Tibshirani 1996).
We next examined the ability of each method to identify either 2, 5, or 10 simulated causal eQTL variants at each gene. As expected, for all numbers of causal eQTL variants, the sparse polygenic models and BIMBAM all had higher recall than single-variant association analysis for any value of precision (Figure 1, B–D), most likely due to the ability of these models to associate multiple variants simultaneously, rather than associating each variant individually as in single-variant association analysis. Out of all five models, BSLMM consistently achieved the highest precision and recall along all points on the PR curve; for example, BSLMM outperformed single-variant association analysis in recall by 1.6- to 5.2-fold at 20% precision (Figure 1, B–D). Additionally, while BIMBAM outperformed single-variant association analysis, it performed worse than the three sparse polygenic models at almost all points on the PR curve, most likely due to the need to limit its input data to the 100 highest ranked eQTL SNPs identified by single-variant association analysis for computational feasibility. Specifically, the 100 highest ranked single-variant association analysis eQTL SNPs only contained 70.4%, 45.5%, and 32.5% of the truly causal eQTL variants with 2, 5, or 10 simulated causal eQTL variants, respectively; therefore, these values were an upper bound on the number of causal eQTL variants that could be identified by BIMBAM. Furthermore, the sparse polygenic models identify low-frequency variants as the top eQTL SNP more often than single-variant association analysis (Figure S2 in File S1). Specifically, considering only the top eQTL SNP, BSLMM identified 1.2-, 1.9-, and 2.3-fold more low frequency variants than single-variant association analysis for 2, 5, or 10 causal variants, respectively. These data show that, between the three sparse polygenic models, BSLMM achieved the best performance throughout its PR curve, followed by Elastic Net, and then Lasso.
Overall, we found that the three sparse polygenic models performed as well as, or, in most cases, better than, fine-mapping and single-variant association analysis. This held true even under the ideal case for single-variant association analysis where there was only one causal eQTL variant per gene; we therefore proceeded to only compare the three polygenic models. The differences between the performance of the three sparse polygenic models is partly due to the fact that they handle the sparseness (polygenic) parameter differently; BSLMM was flexible as it learned the degree of polygenicity as a model parameter (Zhou et al. 2013), whereas Elastic Net had a set parameter to describe polygenicity and Lasso assumed a sparse model (Materials and Methods). Lasso’s underperformance compared with Elastic Net is not only due to strong shrinkage, but also due to it selecting only one of multiple variants in strong LD; thus, if there are two or more truly causal eQTL variants in strong LD, all but one will be missed during the variant selection process (Zou and Hastie 2005). Conversely, as BSLMM and Elastic Net distribute effects across variants in LD, they can identify multiple causal eQTL variants at a gene even when they are in strong LD.
Determining the similarity of eQTL SNPs identified by each model
To quantify the similarity between the eQTL SNPs identified by the different models, we found the overlap of the eQTL SNPs identified by each sparse polygenic model with those identified by single-variant association analysis when we simulated either one or five causal eQTL variants (Figure S3 and Figure S4 in File S1). When simulating a single causal eQTL variant, and considering only the top eQTL SNP identified with each method, we found moderate overlap between single-variant association analysis, and each of the three sparse polygenic models (BSLMM 588 SNPs; 58.8%; Elastic Net 569 SNPs; 62.9%; Lasso 604 SNPs; 65.6%; Figure S3A in File S1). Interestingly, the magnitude of overlap between the sparse polygenic models and single-variant association analysis was larger than the recall of single-variant association analysis (45%; Figure 1A), suggesting that the models tend to choose the same incorrect eQTL SNPs. When considering the 20 highest ranked eQTL SNPs identified by each method, the percentage of overlapping eQTL SNPs with single-variant association analysis decreased for BSLMM (7490 SNPs; 37.5%) and increased for Elastic Net (7765 SNPs; 79.3%) and Lasso (1862 SNPs; 79.6%) (Figure S3B in File S1). This decrease for BSLMM is likely due to it jointly associating variants with gene expression, and these increases for Elastic Net and Lasso are likely due to the shrinkage performed by them. When identifying five simulated causal eQTL variants, the eQTL SNPs identified by the sparse polygenic models had relatively low overlap with those identified by single-variant association analysis, regardless of whether only the top eQTL SNP was considered (range: 35.1–53.7%), or if the 20 highest ranked eQTL SNPs were considered (range: 33.0–49.6%) (Figure S4 in File S1). Overall, these analyses reveal that the eQTL SNP sets chosen by the various models are substantially different.
BSLMM performs robustly under suboptimal conditions
We examined how well sparse polygenic models performed compared to single-variant association analysis under suboptimal conditions. With either few samples (100) or low heritability (20%), all methods performed similarly with one simulated causal eQTL variant per gene; however, BSLMM had the highest precision and recall as the number of simulated causal eQTL variants increased (Figure S5 and Figure S6 in File S1). When simulating both few samples and low heritability, BSLMM and single-variant association analysis had similar precision and recall regardless of the number of simulated causal eQTL variants (Figure S7 in File S1). These results show that BSLMM performs equally well or better than single-variant association analysis under suboptimal experimental conditions.
Overall, using simulated data, BSLMM and single-variant association analysis performed similarly when there was one causal eQTL variant per gene, but BSLMM performed better when there were multiple causal eQTL variants per gene, likely due to it intrinsically capturing LD structure through multiple regression, learning the degree of polygenicity from the data, and identifying low-frequency eQTL SNPs.
eQTL SNP discovery from 131 iPSC samples
To assess the ability of sparse polygenic models to identify causal eQTL variants in real data, we identified eQTL SNPs from gene expression data from 131 iPSC samples and WGS data generated from the corresponding individuals enrolled in the iPSCORE cohort (DeBoever et al. 2017; Panopoulos et al. 2017) (Materials and Methods). With single-variant association analysis, we identified 3442 out of 17,819 expressed autosomal genes with at least one associated SNP within 1 MB of the TSS at 5% FDR. Among the 3442 eGenes, 2237 had a single eQTL SNP, and 205 had two independent eQTL SNPs (identified by conditioning on the genotype of the highest SNP at 5% FDR). For each of the three sparse polygenic models, we quantified how many eQTL SNPs were identified for the 3442 eGenes identified by single-variant association analysis, and measured the extent to which each set of eQTL SNPs overlapped with those identified with single-variant association analysis. As BSLMM gives weight to the most likely SNP tested at each gene (22,095,885 SNP-gene pairs in total), it identified at least one eQTL SNP for each of the 3442 eGenes; elastic net identified 47,285 SNP-gene pairs for 2728 (79%) of the eGenes, and Lasso identified 11,314 SNP-gene pairs for 2777 (81%) of the eGenes. Notably, due to shrinkage, Lasso and Elastic Net identified <20 eQTL SNPs for each eGene on average (Elastic Net: 16.1; Lasso; 3.7), similar to the simulation data. These results show that the three sparse polygenic models identify eQTL SNPs for the majority of the genes with significant associations identified with single-variant association analysis.
Overlap analysis of eQTL SNPs
We examined the similarity in the eQTL SNPs identified by each of the three sparse polygenic models and single-variant association analysis. Considering only the top SNP at each of the 3237 eGenes with one eQTL SNP, the three sparse polygenic models all showed moderate overlap with single-variant association analysis (BSLMM 1684 SNPs; 52.2%; Elastic Net 1532 SNPs; 60.7%; Lasso 1684 SNPs; 65.5%; Figure S8A in File S1). Considering the 20 highest-ranked eQTL SNPs, the percentage of overlapping eQTL SNPs increases for BSLMM (36,483 SNPs; 56.4%) and Elastic Net (18,966 SNPs; 71.6%), and stays approximately the same for Lasso (5757 SNPs; 64.1%) (Figure S8B in File S1), similar to the simulated data. For the 205 eGenes with more than one independent eQTL SNP, the top SNP identified with BSLMM overlapped less (71 SNPs; 34.6%) with those identified by single-variant association analysis compared to Elastic Net (97 SNPs; 47.5%) and Lasso (128 SNPs; 62.4%) (Figure S9A in File S1). When the 20 highest ranked variants are considered, eQTL SNPs identified with BSLMM (1722 SNPs; 42.0%) and Elastic Net (1900 SNPs; 57.6%) are more overlapping, while those identified with Lasso (735 SNPs; 44.4%) are less (Figure S9B in File S1). These results show that when there is more than one independent eQTL SNP per gene, the variants identified with each of the sparse polygenic models have relatively low overlap with the variants identified with single-variant association analysis (34.6–62.4%), similar to the simulated data. This low level of overlap is expected, as the sparse polygenic models can identify multiple causal SNPs jointly per gene, whereas single-variant association analysis cannot. These overlap analyses show that while the three polygenic models identify eQTL SNPs for the majority of eGenes identified with single-variant association analysis, many of the identified eQTL SNPs are different.
BSLMM identifies more eQTL SNPs with low MAF
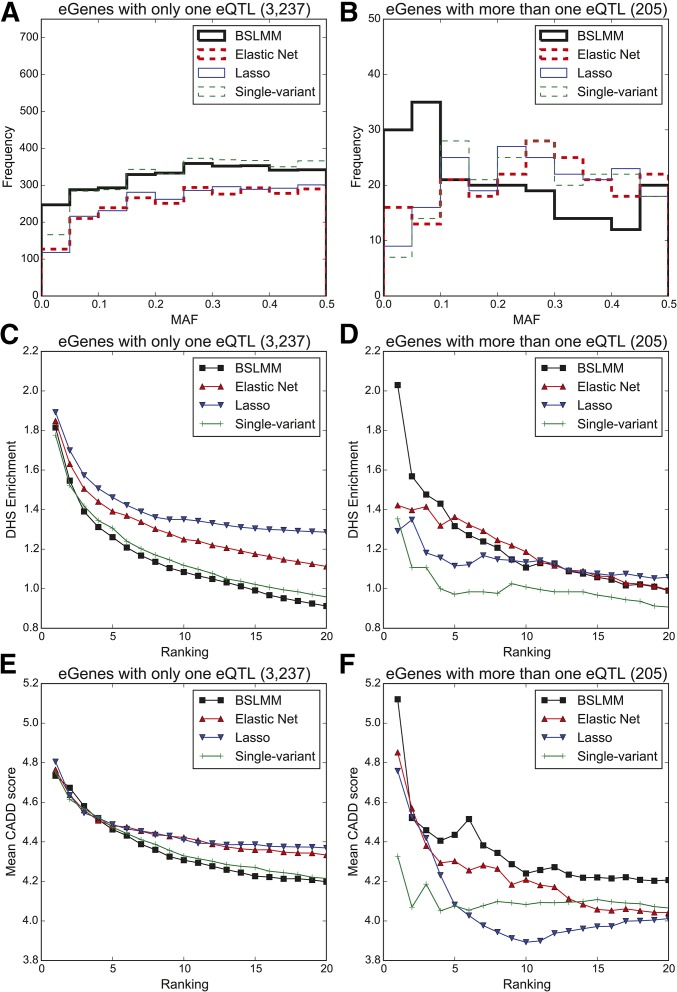
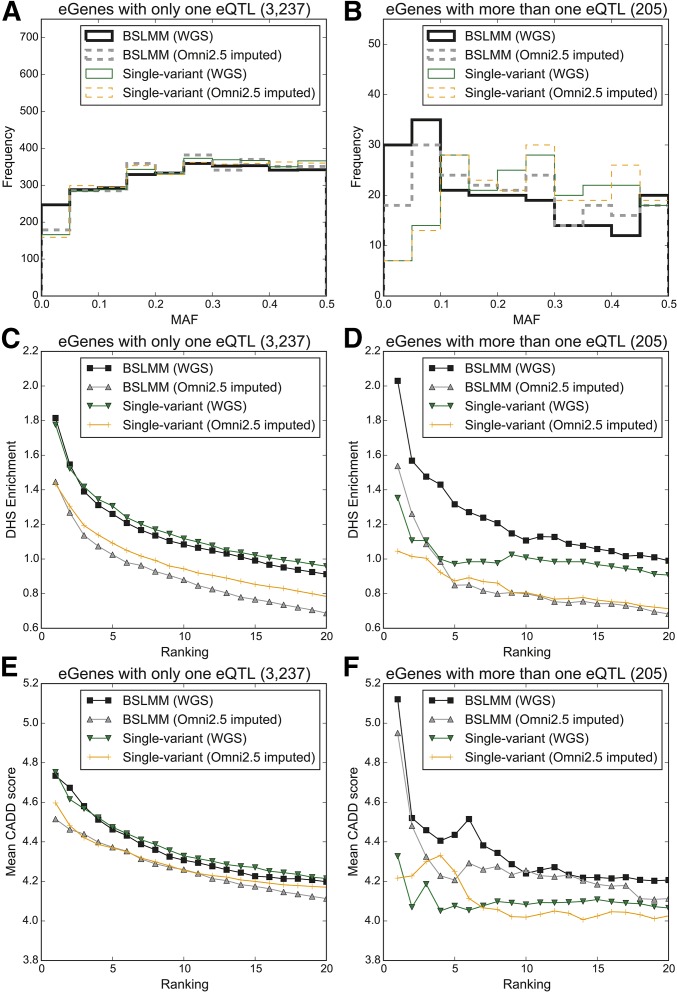
To assess the ability of each method to identify low-frequency eQTL SNPs, we compared the MAF of the eQTL SNPs identified with single-variant association analysis to those identified by the three sparse polygenic models. While both BSLMM and single-variant association analysis identified an eQTL SNP at each eGene, more BSLMM highest ranked eQTL SNPs (240, 7.6%) were low-frequency compared to single-variant association analysis highest ranked eQTL SNPs (166, 5.1%; Figure 2A). On the other hand, Elastic Net and Lasso discovered eQTL SNPs for ∼80% of the eGenes, and the MAF distribution of the variants identified were similar to those identified by single-variant association analysis (Figure 2, A and B). The difference between the number of identified low frequency eQTL SNPs with BSLMM and single-variant association analysis was more pronounced at the 205 eGenes with more than one independent eQTL: 30 (14.6%) of the highest ranked eQTL SNPs by BSLMM were low frequency (MAF <5%), compared to seven (3.4%) identified with single-variant association analysis (Figure 2B). This difference is likely from prioritizing eQTL SNPs from single-variant association analysis by P-value, which is lower for high frequency variants (Wakefield 2009), and prioritizing eQTL SNPs from BSLMM by effect size, which is less likely to be affected by allele frequency.
Figure 2.
eQTL variant discovery from 131 iPSC samples with BSLMM, Elastic Net, Lasso, and single-variant association analysis. MAF spectrum of candidate eQTL SNPs identified with BSLMM, Elastic Net, Lasso, and single-variant association analysis for (A) genes with only one eQTL, and (B) genes with more than one independent eQTL. Enrichment of the identified eQTL SNPs, with varying ranked thresholds (from 1 to 20 per gene), in DHSs for (C) genes with only one eQTL, and (D) genes with more than one independent eQTL. Deleteriousness of the identified eQTL variants measured by CADD score for (E) genes with only one eQTL, and (F) genes with more than one independent eQTL.
Functional characterization of eQTL SNPs
We evaluated the potential functional impact of identified eQTL SNPs by examining how likely they were to affect gene regulation by measuring overlap with iPSC DHSs (Degner et al. 2012), and their deleteriousness based on CADD score (Kircher et al. 2014). At genes with a single eQTL SNP per eGene, when considering only the highest ranked eQTL SNP per eGene, similar DHS enrichment (range: 1.78- to 1.89-fold) and mean CADD scores (range: 4.73–4.81) were observed across all models. When considering the 20 highest ranked eQTL SNPs, Elastic Net and Lasso identified eQTL SNPs with higher DHS enrichment (Figure 2C) and mean CADD scores (Figure 2E) than those identified with single-variant association analysis and BSLMM. These observations are most likely due to the shrinkage Elastic Net and Lasso perform, and suggest that they tend to only identify the most strongly associated eQTL SNPs, which, in turn, are expected to have higher DHS enrichment and mean CADD scores (Figure 2, C and E). At the 205 eGenes with more than one independent eQTL SNP, BSLMM identified substantially more variants overlapping DHSs than all other methods when considering the single highest ranked eQTL SNP (BSLMM 33, single-variant association analysis 22; Figure 2D), and had the highest mean CADD scores (Figure 2F). Interestingly, 33% of the highest ranked BSLMM eQTL SNPs in DHS peaks had a MAF <10%, compared to 18% from single-variant association analysis. When considering the 20 highest ranked variants, variants identified by the three sparse polygenic models had higher overlap with DHSs and higher mean CADD scores (Figure 2, D and F); across most of the ranked thresholds, BSLMM eQTL SNPs showed the highest CADD scores. BSLMM's superior performance is most likely due to ability to capture LD, and the shrinkage performed by Elastic Net and Lasso; we therefore primarily focused on comparison between single-variant association analysis and BSLMM for the following analyses.
Gene expression heritability analysis
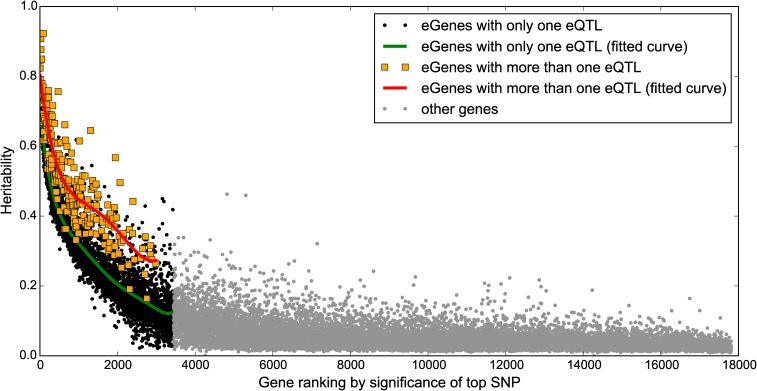
One of the important purposes of an eQTL study is to characterize the heritability of gene expression levels. BSLMM can estimate narrow-sense heritability of genes by estimating the proportion of variance in phenotypes explained (PVE) (Zhou et al. 2013); we therefore examined the heritability of expression for each of the 17,819 expressed autosomal genes with BSLMM using the genotypes of the cis-SNPs within 1 Mb of each gene’s TSS. Out of the 17,819 genes, 2264 had a heritability >0.2, and 2168 (95.8%) of these were also identified as eGenes at FDR <5%. In general, we observed a high correlation between the BSLMM estimated heritability of gene expression and the significance of eQTL SNPs from single-variant association analysis (Spearman’s rank correlation: −0.73, P-value <1.0 × 10−3, Figure 3), suggesting highly heritable genes are likely to be identified with single-variant association analysis as eGenes, and vice versa. Interestingly, we found that genes with more than one independent eQTL SNP had larger heritibilities on average (0.51) than eGenes with one eQTL SNP (0.26), suggesting that BSLMM may be able to identify a larger number of highly heritable genes.
Figure 3.
Identification of genes with heritable expression levels. Genes ranked based on the significance level of the highest ranked eQTL SNP. The x-axis shows the ranking of genes, and the y-axis shows the narrow-sense heritability estimated with BSLMM. Genes with more than one independent eQTL (orange squares) tend to have higher heritability than those with only one eQTL (black circles).
Prioritization of eQTL SNPs associated with pluripotency marker gene expression
To further investigate how BSLMM performed compared to single-variant association analysis, we examined intervals encoding nine previously identified pluripotency marker genes (Tsankov et al. 2015) known to be functionally important in human pluripotent stem cells. Single-variant association analysis identified eQTL SNPs for five of the genes that had relatively high heritability estimates with BSLMM: OCT4 (heritability = 0.442), CXCL5 (heritability = 0.444), IDO1 (heritability = 0.293), HESX1 (heritability = 0.084), and SOX2 (heritability = 0.117). The other four genes, DNMT3B (heritability = 0.039), LCK (heritability = 0.046), TRIM22 (heritability = 0.0898), and NANOG (heritability = 0.069), did not have significant eQTL SNPs at FDR <5%.
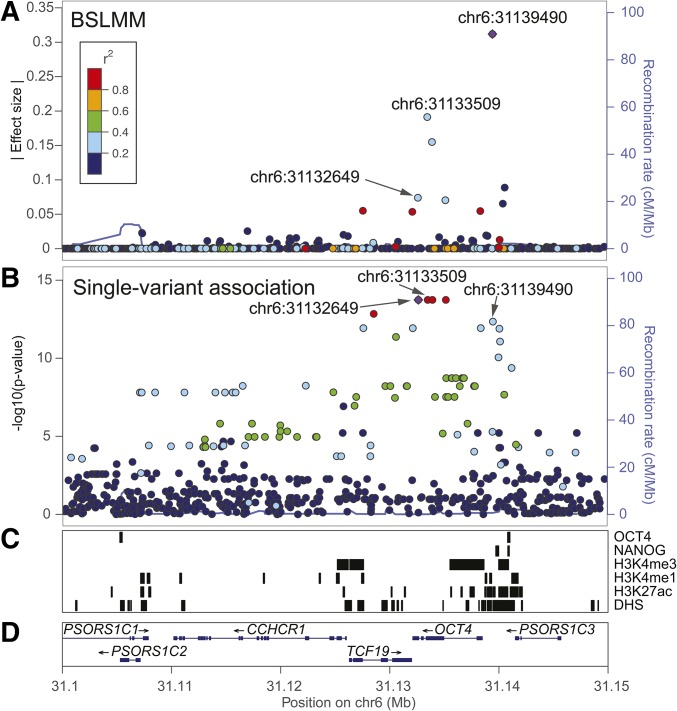
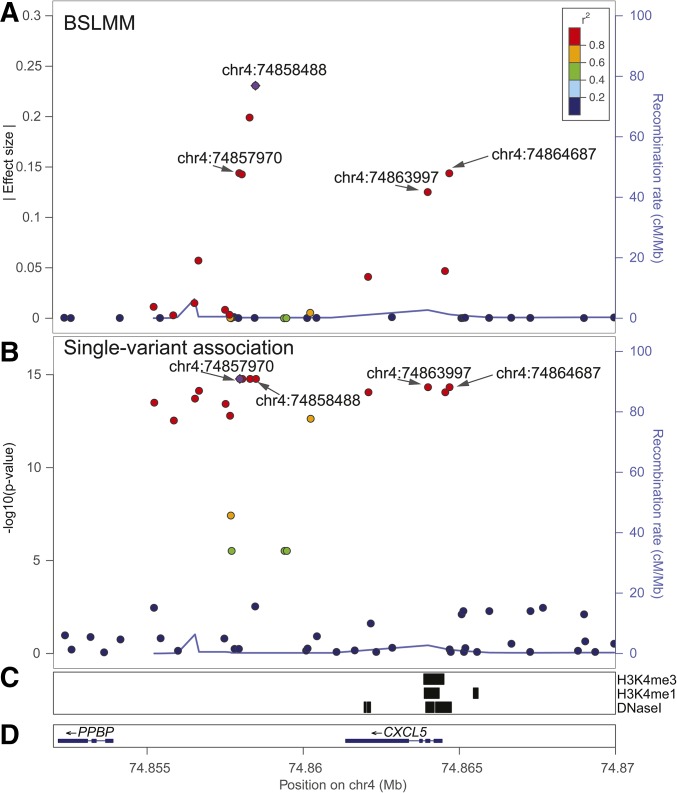
We ranked candidate eQTL SNPs with both BSLMM and single-variant association analysis at the interval encoding OCT4, a factor used in the reprogramming iPS cells (Takahashi et al. 2007); Figure 4A and B). The highest ranked BSLMM eQTL SNP at chr6:31139490 had a relatively high effect size (0.312), and was in relatively low LD with the second highest ranked SNP at chr6:31133509 that had a much lower effect size (<0.20). We examined the functional annotations of the interval and found that the highest ranked SNP was located in an interval overlapping an iPSC DHS site, and was near multiple NANOG binding sites, suggesting that OCT4 has at least one, and maybe two (with one in each LD group), independent eQTL SNP(s). Single-variant association analysis (Figure 4B) identified a different SNP, chr6:31132649, as the most significantly associated variant (P-value = 1.83 10−14); notably, there were three other variants that were in high LD with chr6:31132649 and had similar P-values. For IDO1, BSLMM identified two candidate eQTL SNPs in strong LD. The variant with the second largest effect size (chr8:39807281) overlapped both an iPSC DHS and H1 hESC OCT4 binding site (Figure S10 in File S1), and was also identified as the highest ranked SNP with single-variant association analysis. For CXCL5, single-variant association analysis identified four variants tied with the lowest P-value (1.68 10−15)—chr4:74857970, chr4:74858051, chr4:74858300, and chr4:74858488—and identified two variants—chr4:74864687 and chr4:74863997—tied with the second lowest P-value (4.70 10−15). BSLMM identified the same set of candidate eQTL SNPs at CXCL5, though the exact ranking of the six SNPs was slightly different (chr4:7485488, chr4:74858300, chr4:74857970, chr4:74864687, chr4:74858051, and chr4:74863997) due to the random sampling that occurs in the MCMC algorithm that BSLMM uses (Materials and Methods). Although all candidate SNPs were in strong LD, and had relatively large effect sizes, two of them (chr4:74863997 and chr4:74864687) were located in an iPSC DHS site (Figure 5). While neither method precisely pinpointed the causal eQTL variant in the CXCL5 interval, BSLMM provided a much narrower candidate list based on effect size for further validation.
Figure 4.
eQTL variants identified associated with OCT4 expression. Variants are color-coded based on the strength of LD with the most highly associated eQTL (purple diamond). (A) BSLMM ranked eQTL SNPs with varying effect sizes as candidate eQTL variants including chr6:31139490 and chr6:31133509. (B) Single-variant association analysis identified a SNP located on chr6:31132649 as the most significantly associated eQTL SNP, whereas the eQTL SNP located on chr6:31139490 was identified as the sixth significantly associated variant. (C) Genomic regions annotated with H1-hESC OCT4 and NANOG binding site, iPSC histone marks (H3K4me3, H3K4me1, and H3K27ac), and iPSC DHSs. (D) Genomic coordinates of OCT4 and surrounding genes in hg19.
Figure 5.
eQTL variants identified as associated with CXCL5 expression. Variants are color-coded based on the strength of LD with the most highly associated eQTL (purple diamond). (A) BSLMM prioritized six eQTL SNPs, including chr4:74863997, and chr4:74864687 which are in a DHS. (B) Single-variant association analysis identified the eQTL SNP located on chr4:74857970 as the most significantly associated variant. (C) Genomic regions annotated with iPSC histone marks (H3K4me3 and H3K4me1), and iPSC DHSs. (D) Genomic coordinates of CXCL5 and surrounding genes in hg19.
BSLMM outperforms single-variant association analysis using SNP array data
Given that most eQTL studies conducted to date used SNP array data instead of WGS data, we evaluated the ability of BSLMM to prioritize eQTL SNPs using imputed genotypes from a SNP array (The GTEx Consortium 2015). We generated a synthetic array data set in which genotypes at SNP sites on the Illumina Omni2.5 genotyping array were extracted from the genotype data generated from the WGS data of the 131 individuals, and subsequently imputed genotypes from the haplotypes of the individuals in the 1000 Genomes Project Phase 3 data (Materials and Methods) with IMPUTE2 (Howie et al. 2009). As expected, at the 3442 eGenes identified by single-variant association analysis with WGS data, there were fewer low-frequency (MAF <5%) eQTL SNPs identified with the array data, likely due to known difficulties with imputing low frequency variants (Zheng et al. 2015) (Figure 6, A and B). We found BSLMM and single-variant association analysis eQTL SNPs from the WGS data showed substantially higher enrichment in iPSC DHSs and higher CADD scores compared to those identified with the synthetic Omni2.5 imputed SNPs (Figure 6, C–E). Nevertheless, the candidate eQTL SNPs identified with BSLMM using the synthetic Omni2.5 imputed SNP set were more enriched in iPSC DHSs than those identified with single-variant association analysis using synthetic Omni2.5 imputed genotype data sets. These results demonstrate that BSLMM performs better than single-variant association analysis using SNP array data, but using a comprehensive set of variants identified via WGS is substantially better for identifying causal eQTL variants than using SNP array data.
Figure 6.
Comparison of eQTL variant discovery from WGS with simulated SNP array data. MAF spectrum of candidate eQTL SNPs identified with BSLMM or single-variant association analysis, from either from WGS or synthetic SNP array data, for: (A) genes with only one eQTL, and (B) genes with more than one independent eQTL. Enrichment of ranked eQTL variants in DHSs for (C) genes with only one eQTL, and for (D) genes with more than one independent eQTL. Deleteriousness of the identified eQTL variants measured by CADD score for (E) genes with only one eQTL, and for (F) genes with more than one independent eQTL.
Discussion
We evaluated three sparse polygenic models for prioritizing causal eQTL variants through simulated data analyses, and demonstrated the superiority of these methods over conventional single-variant association analysis. When there are multiple causal variants per gene, sparse polygenic models, especially BSLMM, were found to be more effective and robust at prioritizing causal eQTL variants than single-variant association analysis and BIMBAM—a Bayesian fine-mapping method. These findings are possibly due to the fact that BSLMM employs the MCMC method to estimate the effects of each variant at a locus simultaneously, and, at the same time, learns the number of causal eQTL variants from the data in a computationally tractable manner. We also applied three sparse polygenic modeling approaches to real RNA-seq and matching WGS data from 131 iPSC samples, and found that BSLMM identified more low-frequency variants (MAF <5%) than single-variant association analysis. This higher number of prioritized low frequency variants is beneficial, as rare noncoding variants are more likely to be deleterious and have larger effect sizes (1000 Genomes Project Consortium et al. 2012).
By examining the intervals encoding three pluripotency marker genes, we showed that putative regulatory variants associated with gene expression levels are more readily identified with BSLMM than single-variant association analysis. We estimated narrow-sense heritability (h2) of expression for all autosomal genes with BSLMM, and showed that estimated h2 of gene expression is well-correlated with single-variant association analysis P-value. While the computational cost of the MCMC algorithm makes it challenging to obtain statistical significance levels with BSLMM, the top eQTL SNP discovered with single-variant association analysis is often not the causal eQTL variant; it would therefore be beneficial to use BSLMM in conjunction with single-variant association analysis in order to discover the best candidate list of causal eQTL variants.
There are several interesting ways in which sparse modeling approaches can be applied to gain further insights into regulation of gene expression. For instance, it could be possible to incorporate other types of variants, such as insertions, deletions, and copy number variations under the same analytic framework for eQTL SNP discovery. Trans-eQTL SNPs (i.e., variants on different chromosomes) could also be analyzed, but this may be challenging given the small sample sizes currently available (Wheeler et al. 2016). In our real data analysis, in order to handle outliers of gene expression levels, we first conducted quantile-normalization across samples, and then rank-normalization at each gene. Although this is a standard procedure for most eQTL studies conducted to date (The GTEx Consortium 2015), further investigation into whether this is an optimal approach when applying BSLMM is needed, because BSLMM assumes Gaussian noise for gene expression levels. Other types of molecular phenotypes, such as methylation quantitative trait loci (meQTL), histone quantitative trait loci (hQTL) (Grubert et al. 2015) and chromatin accessibility quantitative trait loci (caQTL) (Kumasaka et al. 2016) can be analyzed through a similar sparse polygenic modeling approach.
Supplementary Material
Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.117.300435/-/DC1.
Acknowledgments
We would like to thank Erin Smith for helpful comments on the manuscript. This work was supported in part by a California Institute for Regenerative Medicine (CIRM) grant GC1R-06673 (to K.A.F.) and National Institutes of Health (NIH) grants HG008118-01 (to K.A.F.), HL107442-05 (to K.A.F.) and DK105541 (to K.A.F.).
Footnotes
Communicating editor: J. Akey
Literature Cited
- Auton A., Brooks L. D., Durbin R. M., Garrison E. P., Kang H. M., et al. , 2015. A global reference for human genetic variation. Nature 526: 68–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Battle A., Mostafavi S., Zhu X., Potash J. B., Weissman M. M., et al. , 2014. Characterizing the genetic basis of transcriptome diversity through RNA-sequencing of 922 individuals. Genome Res. 24: 14–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulik-Sullivan B. K., Loh P. R., Finucane H. K., Ripke S., Yang J., et al. , 2015. LD score regression distinguishes confounding from polygenicity in genome-wide association studies. Nat. Genet. 47: 291–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng W., Shi Y., Zhang X., Wang W., 2016. Sparse regression models for unraveling group and individual associations in eQTL mapping. BMC Bioinformatics 17: 136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiang C., Scott A. J., Davis J. R., Tsang E. K., Li X., et al. , 2017. The impact of structural variation on human gene expression. Nat. Genet. 49: 692–699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corradin O., Saiakhova A., Akhtar-Zaidi B., Myeroff L., Willis J., et al. , 2014. Combinatorial effects of multiple enhancer variants in linkage disequilibrium dictate levels of gene expression to confer susceptibility to common traits. Genome Res. 24: 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danecek P., Auton A., Abecasis G., Albers C. A., Banks E., et al. , 2011. The variant call format and VCFtools. Bioinformatics 27: 2156–2158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeBoever C., Li H., Jakubosky D., Benaglio P., Reyna J., et al. , 2017. Large-scale profiling reveals the influence of genetic variation on gene expression in human induced pluripotent stem cells. Cell Stem Cell 20: 533–546.e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Degner J. F., Pai A. A., Pique-Regi R., Veyrieras J. B., Gaffney D. J., et al. , 2012. DNase I sensitivity QTLs are a major determinant of human expression variation. Nature 482: 390–394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J., Hastie T., Tibshirani R., 2010. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 33: 1–22. [PMC free article] [PubMed] [Google Scholar]
- 1000 Genomes Project Consortium. Abecasis G. R., Auton A., Brooks L. D., DePristo M. A., et al. , 2012. An integrated map of genetic variation from 1,092 human genomes. Nature 491: 56–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grubert F., Zaugg J. B., Kasowski M., Ursu O., Spacek D. V., et al. , 2015. Genetic control of chromatin states in humans involves local and distal chromosomal interactions. Cell 162: 1051–1065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guan Y., Stephens M., 2011. Bayesian variable selection regression for genome-wide association studies, and other large-scale problems. Ann. Appl. Stat. 5: 1780–1815. [Google Scholar]
- Hormozdiari F., Kostem E., Kang E. Y., Pasaniuc B., Eskin E., 2014. Identifying causal variants at loci with multiple signals of association. Genetics 198: 497–508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howie B. N., Donnelly P., Marchini J., 2009. A flexible and accurate genotype imputation method for the next generation of genome-wide association studies. PLoS Genet. 5: e1000529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kichaev G., Yang W. Y., Lindstrom S., Hormozdiari F., Eskin E., et al. , 2014. Integrating functional data to prioritize causal variants in statistical fine-mapping studies. PLoS Genet. 10: e1004722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kircher M., Witten D. M., Jain P., O’Roak B. J., Cooper G. M., et al. , 2014. A general framework for estimating the relative pathogenicity of human genetic variants. Nat. Genet. 46: 310–315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumasaka N., Knights A. J., Gaffney D. J., 2016. Fine-mapping cellular QTLs with RASQUAL and ATAC-seq. Nat. Genet. 48: 206–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lappalainen T., Sammeth M., Friedlander M. R., ’t Hoen P. A., Monlong J., et al. , 2013. Transcriptome and genome sequencing uncovers functional variation in humans. Nature 501: 506–511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S. I., Dudley A. M., Drubin D., Silver P. A., Krogan N. J., et al. , 2009. Learning a prior on regulatory potential from eQTL data. PLoS Genet. 5: e1000358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li B., Ruotti V., Stewart R. M., Thomson J. A., Dewey C. N., 2010. RNA-Seq gene expression estimation with read mapping uncertainty. Bioinformatics 26: 493–500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H., Durbin R., 2009. Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics 25: 1754–1760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X., Battle A., Karczewski K. J., Zappala Z., Knowles D. A., et al. , 2014. Transcriptome sequencing of a large human family identifies the impact of rare noncoding variants. Am. J. Hum. Genet. 95: 245–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malo N., Libiger O., Schork N. J., 2008. Accommodating linkage disequilibrium in genetic-association analyses via ridge regression. Am. J. Hum. Genet. 82: 375–385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ongen H., Buil A., Brown A. A., Dermitzakis E. T., Delaneau O., 2016. Fast and efficient QTL mapper for thousands of molecular phenotypes. Bioinformatics 32: 1479–1485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panopoulos A. D., D’Antonio M., Benaglio P., Williams R., Hashem S. I., et al. , 2017. iPSCORE: a resource of 222 iPSC lines enabling functional characterization of genetic variation across a variety of cell types. Stem Cell Reports 8: 1086–1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roadmap Epigenomics C., Kundaje A., Meuleman W., Ernst J., Bilenky M., et al. , 2015. Integrative analysis of 111 reference human epigenomes. Nature 518: 317–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Servin B., Stephens M., 2007. Imputation-based analysis of association studies: candidate regions and quantitative traits. PLoS Genet. 3: e114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi K., Tanabe K., Ohnuki M., Narita M., Ichisaka T., et al. , 2007. Induction of pluripotent stem cells from adult human fibroblasts by defined factors. Cell 131: 861–872. [DOI] [PubMed] [Google Scholar]
- Tao H., Cox D. R., Frazer K. A., 2006. Allele-specific KRT1 expression is a complex trait. PLoS Genet. 2: e93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The GTEx Consortium , 2015. The genotype-tissue expression (GTEx) pilot analysis: multitissue gene regulation in humans. Science 348: 648–660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R., 1996. Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. B 58: 267–288. [Google Scholar]
- Tsankov A. M., Akopian V., Pop R., Chetty S., Gifford C. A., et al. , 2015. A qPCR ScoreCard quantifies the differentiation potential of human pluripotent stem cells. Nat. Biotechnol. 33: 1182–1192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van der Auwera G. A., Carneiro M. O., Hartl C., Poplin R., Del Angel G., et al. , 2013. From FastQ data to high confidence variant calls: the genome analysis toolkit best practices pipeline. Curr. Protoc. Bioinformatics 43: 11.10.1–11.10.33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakefield J., 2009. Bayes factors for genome-wide association studies: comparison with P-values. Genet. Epidemiol. 33: 79–86. [DOI] [PubMed] [Google Scholar]
- Wheeler H. E., Shah K. P., Brenner J., Garcia T., Aquino-Michaels K., et al. , 2016. Survey of the heritability and sparsity of gene expression traits across human tissues. bioRxiv: 043653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng H. F., Rong J. J., Liu M., Han F., Zhang X. W., et al. , 2015. Performance of genotype imputation for low frequency and rare variants from the 1000 genomes. PLoS One 10: e0116487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou X., Carbonetto P., Stephens M., 2013. Polygenic modeling with Bayesian sparse linear mixed models. PLoS Genet. 9: e1003264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou H., Hastie T., 2005. Regularization and variable selection via the elastic net. J. R. Stat. Soc. B 67: 301–320. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All simulated data are available by request to the corresponding author. Genotype calls from the whole genome sequence data are available through NCBI dbGaP: phs001325.v1.p1. The RNA sequencing data are available through dbGaP: phs000924.v1.p1.