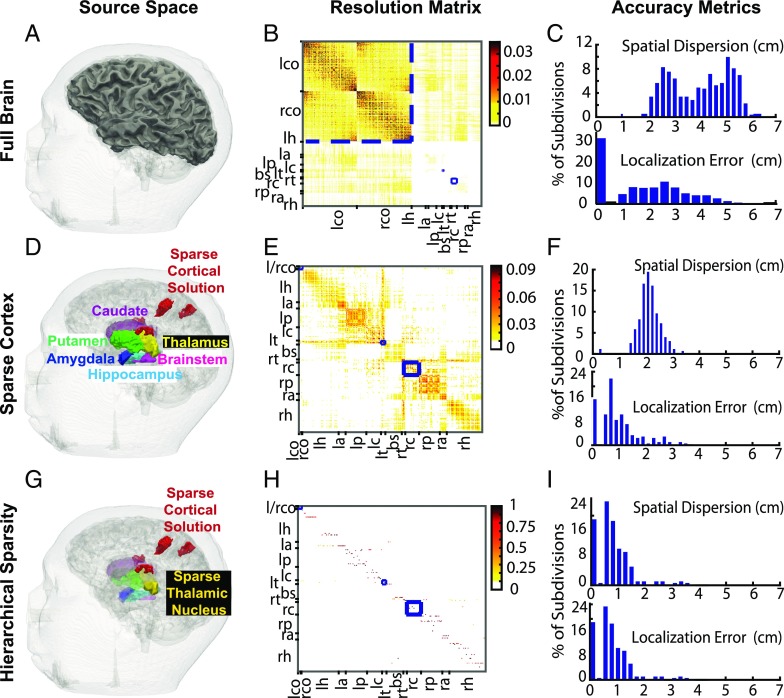
Fig. 4.
An analysis of how sparsity and hierarchy influence subcortical source estimation. (A) Illustration of all brain divisions considered. (B) Minimum-norm estimator (MNE) resolution matrix for the source space in A. (C) Summary dispersion and error metrics for the resolution matrix in B. Cortical estimates concentrate around the diagonal (low localization error), whereas subcortical estimates spread significantly to the cortex (high spatial dispersion). (D) A reduced space composed of sparse cortical regions that generate somatosensory evoked potentials combined with all subcortical volumes. (E and F) MNE resolution matrix and associated performance metrics for the reduced source space in D. The sparse subset of the cortical source space allows subcortical activity to be estimated, albeit with significant spread to nondiagonal regions. (G) Final sparse cortical and subcortical source regions identified using an inverse solution employing sparsity constraints. The faded subcortical regions show the hierarchically reduced subcortical source space, while the foreground subcortical regions show estimated sources in the thalamus. (H and I) Empirical resolution matrix (one active source per column) and associated performance metrics for the sparse solution. Estimates mostly concentrate on and around the diagonal for both cortical and subcortical sources. B, E, and H show left/right (l/r) cortex (l/rco), hippocampus (r/lh), amygdala (r/la), putamen (r/lp), caudate (r/lc), thalamus (r/lt), and brainstem (bs). All resolution matrices order sources based on physical proximity. Therefore, when sources are estimated accurately, the resolution matrix has a diagonal appearance. The blue boxes are used to delineate the position of the cortical, left thalamic, and right caudate sources in the resolution matrices. The changes in the color-scale range highlight the 3−10× increase in recovered source amplitude when sparse estimation is applied across progressively refined hierarchies. Overall, hierarchical sparsity enables focal spatial resolution with minimal dispersion (or point spread) for inverse solutions incorporating both cortical and subcortical sources.