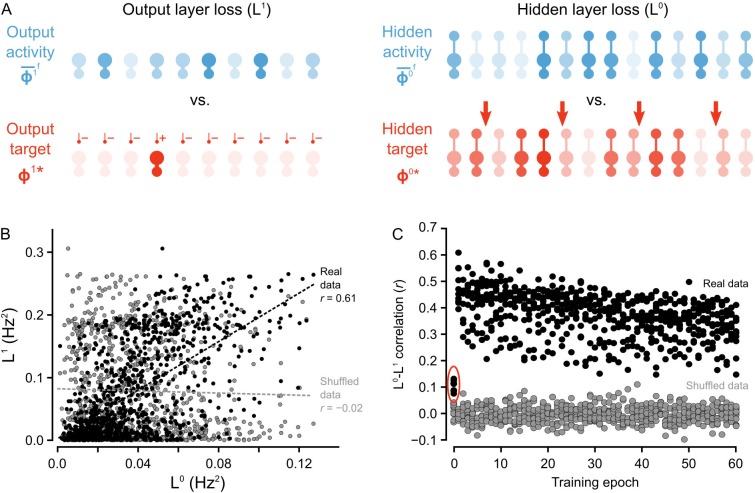
Figure 5. Co-ordinated errors between the output and hidden layers. .
(A) Illustration of output loss function () and local hidden loss function (). For a given test example shown to the network in a forward phase, the output layer loss is defined as the squared norm of the difference between target firing rates and the average firing rate during the forward phases of the output units. Hidden layer loss is defined similarly, except the target is (as defined in the text). (B) Plot of vs. for all of the ‘2’ images after one epoch of training. There is a strong correlation between hidden layer loss and output layer loss (real data, black), as opposed to when output and hidden loss values were randomly paired (shuffled data, gray). (C) Plot of correlation between hidden layer loss and output layer loss across training for each category of images (each dot represents one category). The correlation is significantly higher in the real data than the shuffled data throughout training. Note also that the correlation is much lower on the first epoch of training (red oval), suggesting that the conditions for credit assignment are still developing during the first epoch.
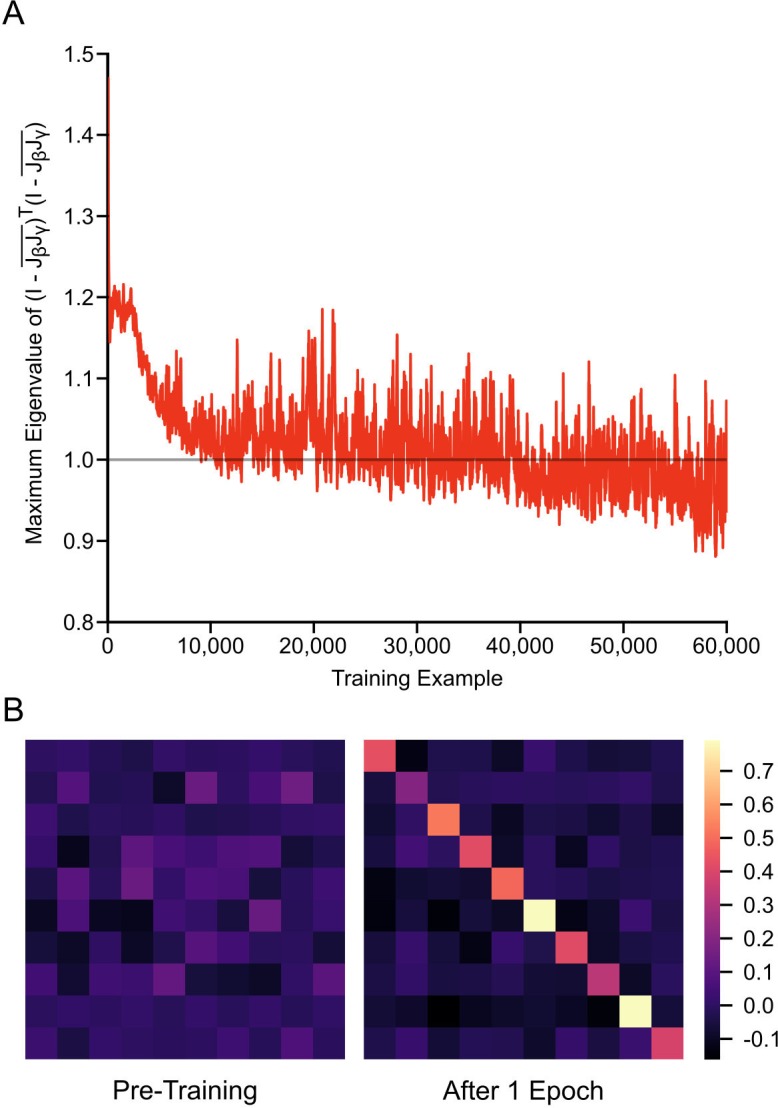
Figure 5—figure supplement 1. Weight alignment during first epoch of training.