Abstract
Mechanically-induced alterations in cardiac electrophysiology are referred to as mechano-electric feedback (MEF), and play an important role in electrical regulation of cardiac performance. The influence of mechanical stress and strain on electrophysiology has been investigated at all levels, however the role of MEF in arrhythmia remains poorly understood. During the normal contraction of the heart, mechano-sensitive processes are an implicit component of cardiac activity. Under abnormal mechanical events, stretch-activated mechanisms may contribute to local or global changes in electrophysiology (EP). While such mechanisms have been hypothesised to be involved in mechanically-initiated arrhythmias, the details of these mechanisms and their importance remain elusive.
We assess the theoretical role of stretch mechanisms using coupled models of cellular electrophysiology and sarcomere contraction dynamics. Using models of single ventricular myocytes, we first investigated the potential MEF contributions of stretch-activated currents (SAC), and stretch-induced myofilament calcium release, to test how strain and fibrosis may alter cellular electrophysiology. For all models investigated, SACs were alone not sufficient to create a pro-arrhythmic perturbation of the action potential with stretch. However, when combined with stretch-induced myofilament calcium release, the action potential could be shortened depending on the timing of the strain. This effect was highly model dependent, with a canine epicardial EP model being the most sensitive.
These model results suggest that known mechanisms of mechano-electric coupling in cardiac myocyte may be sufficient to be pro-arrhythmic, but only in combination and under specific strain patterns.
Keywords: Human electromechanical model, Mechano-electric feedback, Arrhythmia, Computational modelling
1. Introduction
To understand how mechanical changes can lead to arrhythmia, we must consider both the forward (excitation contraction coupling, ECC) and reverse processes (mechano-electric feedback, MEF) that couple electrical activity to mechanical function in cardiac cells and tissue. These interactions play an important role in electrical regulation of cardiac performance due to mechanical changes under normal conditions (Kohl et al., 1999). Yet, despite thorough investigation at all levels, from single ion channels to tissue, (Taggart and Labb, 2008; Lab, 1982, 2006; Sachs et al., 1991; Taggart et al., 1988; Franz et al., 1992; Kohl et al., 2006), the role of these mechanisms in generating arrhythmia is still poorly understood.
During the normal contraction of the heart, mechano-sensitive processes are an implicit component of cardiac activity (Kohl et al., 1999). Under pathological conditions or during mechanical perturbations, stretch-activated mechanisms can alter both processes and contribute to local or global changes in cardiac electrophysiology (EP) (Kohl et al., 1999) and intracellular calcium cycling (Kohl et al., 1999). Stretch may also directly alter calcium cycling independent of sarcolemmal calcium transporters or proximal changes in the myocyte action potential (Prosser et al., 2011, 2013; ter Keurs et al., 1998; ter Keurs et al., 2006). As such, the interplay between forward (EP impacting calcium) and reverse (calcium impacting EP) processes in stretch-induced arrhythmia is intricate and likely to be highly context dependent.
The magnitude of these mechanical effects on EP is not trivial. They are likely to be broadly clinically relevant and in certain circumstances can cause serious dysrhythmia and SCD. Commotio cordis is a prototypical example of a catastrophic stretch-induced arrhythmia initiated by pre-cordial mechanical impact (chest impact). This rare form of arrhythmia has been studied as an uncomplicated case of stretch-induced rhythm disturbance because these events can occur in the absence of morphological heart damage, or other structural or functional cardiac disease (Kohl et al., 2001). A broad range of more common perturbations to normal cardiac mechanics have also been associated with stretch-induced arrhythmia. Structural and functional diseases that cause heterogeneity in mechanical function are chief among these, and include myocardial infarction (MI) and various forms of cardiac dyssynchrony.
In all of these cases, fibrosis and electrical remodelling are likely to be crucial on longer timescales, but over shorter time scales only three mechanisms are thought to be important: (1) induction of stretch-activated currents/channels (SACs) (Healy and McCulloch, 2005), (2) alterations in myofilament calcium sensitivity that can be observed as triggered propagating contractions (TPCs) (Wakayama et al., 2001; ter Keurs et al.,1998; ter Keurs et al., 2006), and (3) alterations in the open probability of intracellular calcium release mechanisms, resulting from signalling processes collectively known as X-ROS (Prosser et al., 2011, 2013).
The potential role of SACs in arrhythmogenesis has been examined experimentally and computationally. These channels are primarily permeable to Na+, K+, and to some degree to Ca2+ and Mg2+ ions (Ruwhof et al., 2001), and they are commonly classified as carrying cation specific or non-selective currents (Ruwhof et al., 2001). Earlier studies have reported variable effects of mechanical activation of SACs on APD in single myocytes, as well as a time-dependent increase in ectopic beats at the tissue level (Trayanova and Rice, 2011; Kohl et al., 1999; Zabel et al., 1996). A consistent observation across these studies was that the effects of acute stretch on cellular and tissue EP were strongly dependent on the timing of the mechanical stimulus in relation to the phase of the action potential (Trayanova and Rice, 2011; Kohl et al., 1999; Zabel et al., 1996).
TPCs (ter Keurs et al., 2006) arise from mechanically induced release of bound calcium from the myofilaments. This process has been observed in a number of experimental preparations including in mechanically damaged regions of isolated rat ventricular and human atrial trabeculae during the normal twitch, or due to rapid changes in myofilament sensitivity elicited by acute application of butane-dione monoxime (BDM) (Wakayama et al., 2005). In each case, release of calcium from the myofilaments propagates through neighbouring tissue by a combination of mechanical transduction, Ca2+ diffusion and Ca2+-induced SR − Ca2+ release (ter Keurs et al., 2006). This triggered detachment of Ca2+ from troponin C (TnC) has been hypothesised to lead to extra-systoles, for which several mechanisms have been suggested, including abnormal SR − Ca2+ release due to damage and abnormal mechanics in non-uniform myocardium (ter Keurs et al., 2006).
Most recently X-ROS signalling has emerged as a new mechanism by which stretch can evoke changes in calcium handling via increased ryanodine receptor (RyR) open probability, and thus may be capable of contributing to MEF (Prosser et al., 2011, 2013). This mechanism was originally observed as an increase in calcium spark frequency resulting from stretch of quiescent myocytes (Prosser et al., 2011, 2013). However, the degree to which X-ROS modulation of RyR may impact stretch-induced arrhythmias is not clear, as it has not been shown to alter twitch calcium transients or induce events associated with calcium-driven arrhythmia. Because it is not yet clear how to interpret X-ROS driven changes in RyR open probability during triggered EC coupling, we did not incorporate these effects into the models and simulations described here.
In addition to these three mechanisms of acute MEF, fibrosis is a key modulator of long term outcomes accompanying abnormal cardiac mechanics in the heart. The healthy rodent (rat, mouse) myocardium is comprised up to 60 – 70% by fibroblasts (Maleckar et al., 2008; Camelliti et al., 2005; Baudino et al., 2006) and it has been shown that fibroblast cell networks communicate electrotonically with myocytes (Maleckar et al., 2008; Kohl et al., 2005; Camelliti et al., 2005; Cabo, 2008), this gap junction-mediated electrotonic coupling is important for cell-to-cell interactions (Maleckar et al., 2008). In pathology, these functional, dynamic interactions can change myocyte excitability and action potential waveform (Maleckar et al., 2008; Baudino et al., 2006; Cabo, 2008; Burstein and Nattel, 2008). It is therefore plausible, if not likely, that electrical and fibrotic remodelling can exacerbate the impacts of acute MEF by providing an arrhythmia-susceptible substrate (McDowell et al., 2011).
The goal of this study was to explore the possible role of these stretch-induced mechanisms in the context of MEF and arrhythmia generation under pathophysiologically realistic strains. To address this goal, we simulated SAC and TPC induction in computational models of single myocytes (from dog and human), and in combination with simulated fibrosis through fibroblast-myocyte coupling. Because the ability for an acute stretch to induce SACs and TPCs should differ greatly depending on when in the cardiac cycle the stretch arrives, we hypothesised that timing of stretch would be critical to determining which of these two mechanisms dominated the electrophysiologic outcomes of MEF. Similarly, because TPCs are dependent upon a precise and dynamic relationship between myofilament calcium binding and cytosolic calcium concentration, we hypothesised that commonly used weakly-coupled formulations of this relationship (described further below) would reduce the impact of stretch-induced calcium feedback on the AP. Our simulations highlight important effects of stretch-timing, species-specificity (electrophysiologic background), and particularly of the formulations used to describe the calcium transfer between the myofilaments and bulk cytosol on MEF outcomes. These findings will be important for future studies of MEF mechanisms and may have important implications for clinical outcomes related to electromechanical dysfunction in the heart.
2. Methods
2.1. Electromechanical myocyte model
Using previously existing membrane ion kinetics and myofilament mechanics models, we constructed coupled electromechanical descriptions for single canine and human myocytes to investigate how mechanical perturbations can give rise to changes in EP. To ensure a strongly coupled system, with feedback from the myofilament model to the ionic model and vice versa, we used a dynamic calcium relationship between the mechanical model and EP where the calcium transient calculated in the ionic model served as input to the myofilament and mechanical changes feed directly into ion flow in the EP system.
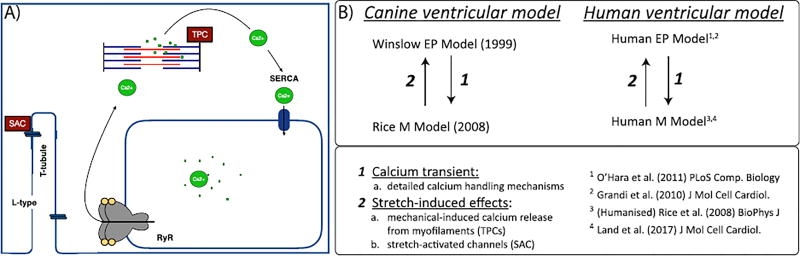
For the myofilament mechanics, we used two models in our coupled systems. The first was the Rice et al. model (Rice et al., 2008), which describes the crossbridge cycling between the thin and thick filament as well as the activation of the thin filament by intracellular calcium through binding to TnC. This crossbridge cycling uses a five state Markov model to give sufficient detail for the biophysical mechanisms and cooperativity. We also used the myofilament model from Land et al. (Land et al., Niederer), which is based on human data, and describes passive viscoelastic response, active tension including thin filament kinetics and crossbridge attachment, length-dependence of tension, steady-state force-pCa and length-dependent response, velocity-dependent response, and isometric twitch response in intact muscle. We coupled these mechanics models to three different EP models; the canine epicardial model from Winslow et al. (1999), and two different human models from Grandi and Bers et al (Grandi et al., 2010). as well as O'Hara and Rudy et al. (OHara et al., 2011).
For feedback between the EP and myofilaments, we used a dynamic term for the intracellular calcium buffering by TnC based on Rice et al. (2008). (see Equation (1) and Equation (2)). The dynamic representation of calcium binding to TnC was necessary to reproduce contractile experiments from Wakayama et al. (2001). (see Fig. 1) and Ji et al. (2015). by ensuring calcium-dependent feedback from the myofilament model to the ionic model. The dynamic calcium buffering via TnC in Rice et al. (2008), determines the fraction of calcium bound to TnC incorporating the cooperativity of TnC calcium-binding. Therefore, the regulation and crossbridge cycling state derivatives are as in the original Rice et al. model (Rice et al., 2008):
| (1) |
| (2) |
with konT (total on rate for calcium binding to TnC), koffLT and koffHT (total off-rates for calcium binding to high- and low-affinity sites of TnC, respectively), TRPNCaL and TRPNCaH (calcium bound to low-and high-affinity sites of TnC, respectively), and Cai (intracellular calcium concentration).
Fig. 1.
A) Schematic image of stretch-induced MEF mechanisms, SACs and stretch induced calcium release, modelled in the cell models. SACs occur at the cell membrane while calcium release from myofilaments occurs intracellularly. In this schematic representation the L-type calcium channel (L-type) is the high-voltage dihydropyridine channel which is responsible for ECC in cardiac cells, the sarco/endoplasmic reticulum Ca2+-ATPase (SERCA) is located next to the SR in myocytes and transfers calcium from the cytosol in the SR under ATP hydrolysis during relaxation, and ryanodine receptors (RyRs) are the cellular mediator of calcium-induced calcium release (CICR).
For the Land et al. model (Land et al., Niederer), we applied the same process for coupling as for the Rice et al. model (Rice et al., 2008). As both the Land model (Land et al., Niederer) and the O'Hara-Rudy model (OHara et al., 2011) do not have low- and high-affinity sites for calcium binding to TnC, in this case the calcium flux from TnC can be modelled as in Equation (3)
| (3) |
with TRPNtot being the total concentration of TnC, and dTRPNCatot the total fraction of calcium bound to TnC.
However, because the Land model does not differentiate between low and high affinity sites of calcium binding to TnC, we subtract the fraction of calcium bound to the high-affinity sites of TnC (in the electrophysiologic model formulation) from the total fraction of calcium bound to TnC taken from the Land model (see Equation (4)).
| (4) |
with HTRPNtot and LTRPNtot (the total concentration of low- and high affinity sites of TnC from the Grandi and Bers model (Grandi et al., 2010)), dTRPNCatot (the total calcium binding to TnC calculated in the Land et al. model (Land et al., Niederer)), and dTRPNCaH (the fractional binding of calcium to the high-affinity sites of TRPN from Grandi-Bers (Grandi et al., 2010)).
Both the Grandi et al. (2010). and Winslow et al. (1999). models use dynamic calcium buffering similar to the approach in Rice et al. (2008). Hence, the dynamic buffering on the high affinity sites in those electrophysiological models could be directly replaced by the one calculated in the myofilament model (see Equation (5)) to ensure a strongly coupled system.
| (5) |
with dHTRPNCa (the fractional binding of calcium to the high-affinity sites of TRPN from the EP model), HTRPNtot (the total concentration of high TnC from the EP model), dTRPNCaL (the low-affinity sites of calcium binding to TnC in Rice et al. (2008)), and LTRPNtot (total concentration of low TnC in Rice et al. (2008)).
However, in the O'Hara-Rudy model (OHara et al., 2011), calcium buffering on TnC is a steady state approximation for the combined calmodulin-TnC buffering scheme. Therefore, to create dynamic feedback from the myofilaments to the ionic model in this coupled model, we separated the combined buffering term into calcium binding to TnC and calcium binding to calmodulin.
We kept the steady state term for calmodulin while using the dynamic calcium buffering approach from the Rice et al. model (Rice et al., 2008) for TnC (see Equation (6)). This is consistent with the work of Oliveira et al. and Zile et al. (de Oliveira et al., 2013; Zile and Trayanova, 2016).
Therefore the change in intracellular calcium becomes:
| (6) |
with the updated buffer capacity for calmodulin
| (7) |
and the dynamic buffering from calcium to TnC
| (8) |
with TRPNCaL and TRPNCaH (calcium bound to low- and high-affinity sites of TnC, respectively, from Rice et al. (2008)), and HTRPNtot and LTRPNtot (total troponin concentration of high and low affinity sites, respectively, from Rice et al. (2008)).
Removing the dynamic calcium buffering calculated in the myofilament model from the EP model, and using the original calcium buffering calculations from each model creates a weakly coupled system. Such systems only have feedforward regulation from the EP to the myofilament model but not vice versa. We compared the results from our strongly coupled system to such weakly coupled systems to examine the importance of myofilament calcium feedback on APD.
Starting with the suite of strongly coupled models, we next incorporated stretch-activated channels and stretch-induced myofilament calcium release mechanisms into these systems. To implement SAC activity, we used the method of Healy et al. (Healy and McCulloch, 2005). This approach uses an ionic model of stretch-activated and stretch-modulated currents that differentiates between non-specific cation-selective stretch-activated current Ins and cation-specific stretch-activated current IK0. We implemented SAC activity in a linear manner such that SACs only open when under positive strain (see Fig. 1 and Equation (9)).
| (9) |
with GK0 = 0.8, Gns = 0.024, and Ens = −10.
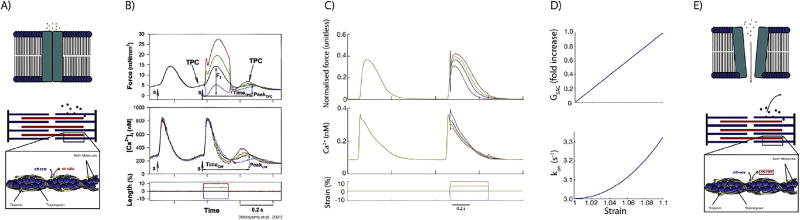
In addition to SACs, we implemented stretch-induced calcium release from the myofilaments. Prior work from Wakayama et al., shows that the relaxation of stretch results in myofilament calcium release due to shortening-induced changes in myofilament calcium sensitivity (Wakayama et al., 2001) (see Fig. 2).
Fig. 2.
Schematic image of stretch-induced calcium release mechanisms: A) SAC and TPC unstretched; E) SAC and TPC stretched; B) Experimental Data from Wakayama et al. including their stretch protocol; C) Computational results fitted to Wakayama et al.’s data; D) development of SAC and TPC dependent on extension ratio.
These experiments showed that the calcium transient slightly decreased on the positive going phase of the stretch while calcium release was triggered when stretch was released. To achieve dissociation replicating the calcium and force profiles measured in these experiments, we modified the on-rate of calcium binding to TnC from a constant to a function depending exponentially on strain (see Fig. 2 and Equation (10)). To achieve the same dynamics as observed by Wakayama et al. (2001), the affinity of TnC for calcium needed to be decreased during stretch, and because we chose an exponential function for this relation, it was only possible to achieve these dynamics through strain-dependent modulation of the on-rate for calcium binding to TnC (see Equation (10)).
| (10) |
with constkonT a model-specific constant for calcium binding to TnC. Specifically, constkonT is unity for the coupling to Grandi-Bers (Grandi et al., 2010) and O'Hara - Rudy (OHara et al., 2011) while constkonT = 1.05 for the Winslow model (Winslow et al., 1999).
In addition to the extension ratio, we also considered changes in calcium affinity depending on active tension which has been experimentally explored by Allen and colleagues (Allen and Kurihara, 1980, 1982; Allen and Kentish, 1985). Therefore, we calculated the stresses due to deformation of the cardiomyocyte in response to contraction and relaxation. Yaniv et al. (2011). showed that the degree of deformation anisotropy between the orthogonal short-axes of a whole cell, during electrical stimulation, coincides with the deformation of mitochondria and sarcomere measurable by confocal microscopy. Due to the dependence of the deformation of the cross sectional area in both width-directions of the sarcomere on the deformation of the mitochondria (Yaniv et al., 2011), in contrary to Yaniv et al., we used the estimation of constant sarcomere volume, Vsarc, during a single contraction transient and ellipsoidal geometry instead of the mitochondrial volume (see Equation (11)).
| (11) |
where D = 2·0.97 is the average sarcomere diameter (with 0.97 is the average mitochondrial diameter), Δdi is the change in diameter due to the deformation along the respective orthogonal reference-axis, and c = 3.7 denotes the ratio for anisotropy. To obtain the relationship between mitochondrial deformation in the width- and in the length-axes, rearrangement of Equation (11) (D, Δdi > 0) leads to
| (12) |
Hence, the stress is
| (13) |
with cross sectional area of a sarcomere.
For the strain formulation of our coupled electromechanical model, we used the same formulation for the calcium release from the myofilament as in Equation (10) while keeping the strain dependent SAC formulation.
2.2. Humanisation of myofilament myocyte model
The Rice et al. (2008). model is based on rabbit data and in order to test whether this had an effect on our MEF mechanisms, we changed the force development to produce more human like twitch dynamics. This was done through modifying the parameters controlling the crossbridge cycling and the calcium-induced activation of the thin filament in a similar manner to that done in de Oliveira et al (de Oliveira et al., 2013; Zile and Trayanova, 2016). (see Table 1).
Table 1.
Humanisation of the Rice model is based on de Oliveira et al. (de Oliveira et al., 2013; Zile and Trayanova, 2016) (upper table) and changes to match the force to the human (lower table).
| Parameter | Units | Value |
|---|---|---|
| knp | ms−1 | 0.61 |
| kpn | ms−1 | 0.016 |
| fapp | ms−1 | 4.8 |
| gapp | ms−1 | 0.093 |
| hf | ms−1 | 0.010 |
| hb | ms−1 | 0.034 |
| gxb | ms−1 | 0.030 |
| hf | ms−1 | 0.015 |
| kon | ms−1 | 0.15 |
| koffH | ms−1 | 0.05 |
| koffL | ms−1 | 0.5 |
While de Oliveira et al. and Zile et al., both used a different implementation for EP (ten Tusscher et al. (Ten Tusscher et al., 2004) and ten Tusscher and Panfilov, (Ten Tusscher and Panfilov, 2006a), respectively), our coupled models based on alternative EP formulations required additional alterations to the calcium based thin filament activation. Specifically, we increased the transition rate between the pre-force and force states in the Markov model of the humanised myofilament model, hf, by 150% to obtain the correct peak force (see lower part of Table 1).
In addition, in order to match our simulations to the experimental data from Wakayama et al. (2001), we needed to decrease the thin filament activation. Therefore, the parameter that is responsible for the binding affinity of calcium to the high and low affinity sites on TnC, kon, was increased by 300%. To be in the physiological range for human values of time to relaxation (Mulieri et al., 1992 (Mulieri et al., 1992); Pieske et al., 1996 (Pieske et al., 1996)), we further increased the off-rate for calcium binding to the high and low-affinity sites for TnC, koffH and koffL respectively, by 200% (see lower part of Table 1).
2.3. Incorporation of fibrosis
To incorporate the myocyte-fibroblast interactions, we used the active version 1 model of Maleckar et al. (2009), in which the electrophysiological properties of the fibroblasts are modelled by five time- and voltage-dependent active membrane conductances. This model incorporates the current flowing through the gap junction between myocyte and fibroblast as well as the movement of Na+ and K+ though the gap junction (for the detailed formulation see Maleckar et al. (2009). This ”active” model includes membrane capacitance as well as four membrane ionic currents; time- and voltage-dependent fibroblast K+ current (IKv), inward-rectifying K1 current (IK1) in the fibroblast which is also highly expressed in cardiacmyofibroblasts, Na+-K+ pump current (INaK) in the fibroblast which has highly expressed K+ channels that result in K+ fluxes, and background Na1 current (Ib,Na) in the fibroblast to balance the Na+ efflux from the Na+ - K+ pump activity (for details refer to MacCannell et al. (2007).
2.4. Stretch protocol
To obtain steady state, we used a dynamic pacing protocol executed with pacing at a cycle length of 1000 ms for 200 beats. A stretch of the myocyte was modelled as a change of sarcomere length up to 10% stretch by increasing the sarcomere length as an exponential (see Fig. 2). This stretch pattern was used to have a continuous differential function. We began by timing electrical stimulation to coincide with peak strain, thus simulating myocyte pre-stretch. However, we also shifted the timing of stretch to investigate the electrophysiologic outcomes of stretch timing. For this study, we chose transient stretches which may occur in cases where dyssynchrony is present (e.g. conduction abnormalities) and resulting non uniform contraction produces heterogeneous strain patterns. This is motivated by the experimental observations that non uniform contraction has a direct relationship to electrical disturbances and the potential generation of arrhythmias (Miura et al. (2010)).
3. Results
3.1. MEF outcomes are strongly species-dependent
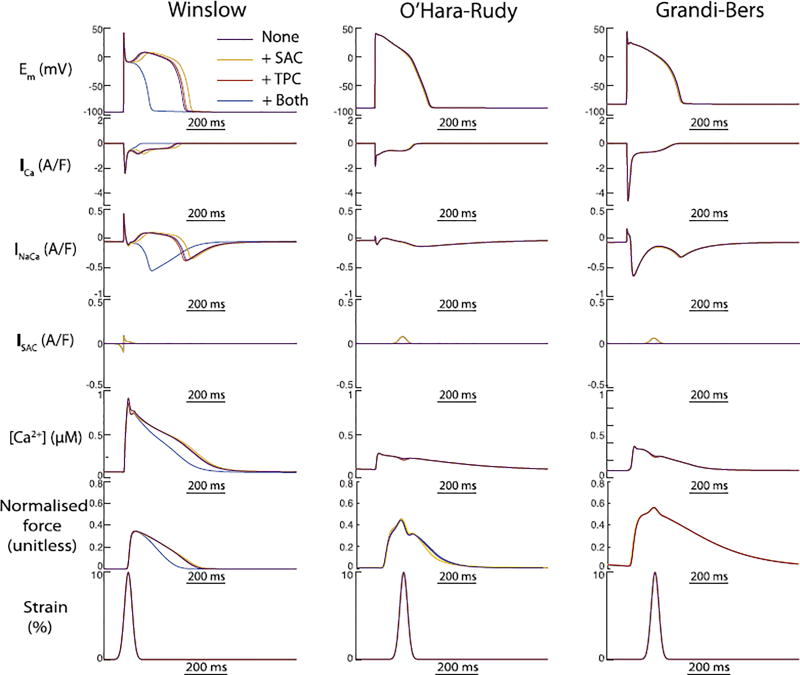
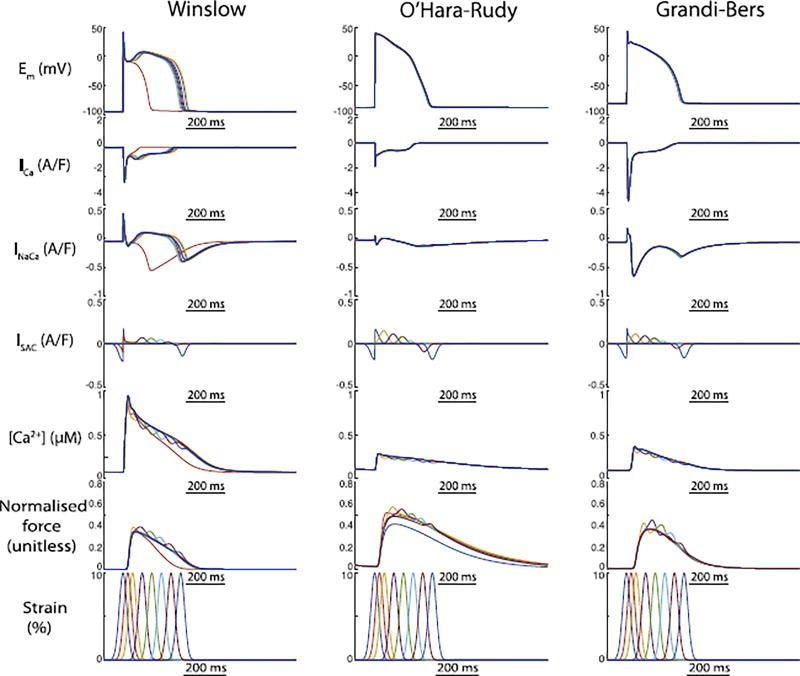
Our initial simulations of these three coupled models investigated how their differing EP formulations interacted with SAC channel activation and TPCs under simulated pre-stretch. Our intention was to understand whether the two MEF mechanisms alter AP morphology similarly or counteract each other, and whether this interaction depends upon the foundation EP model. In both human models, action potentials initiated at peak strain, and including both MEF mechanisms, were almost indistinguishable from those without any externally applied stretch. This was not due to counteraction of the two MEF mechanisms, as the AP morphology remained similar when either was removed (Fig. 4, middle and right columns). In contrast, the canine model exhibited large changes in APD, particularly when both MEF mechanisms were included. In isolation, both mechanisms slightly prolonged the AP (Fig. 4 and Fig. 3). However, when combined these two MEF mechanisms reached a critical point in the repolarisation space where they were able to eliminate the characteristic dome of the canine epicardial AP and sharply abbreviated the AP - 90% repolarisation time was reduced by 180 ms relative to the reference AP (no MEF). The large Ito in the Winslow model is a well-known characteristic of canine epicardial myocytes, and would be expected to predispose the cell to early AP termination for stretches applied very early in the AP, but other important differences exist between this canine model and the two human myocyte models. In particular, the canine model exhibits exaggerated calcium cycling, for which intracellular calcium reaches a peak that is approximately 2.5 fold higher than in either human model.
Fig. 4.
The outcomes of both MEF mechanisms on AP duration is sharply magnified in the canine epicardial model compared to both human models. Individual effects of SAC activation (yellow) and TPC (red) abbreviated and prolonged the AP, respectively. When combined (blue), the two mechanisms interacted to exaggerate the SAC-induced shortening to an extent capable of preventing the canine epicardial dome morphology. In contrast, neither MEF mechanism induced meaningful alterations in repolarisation of either human model.
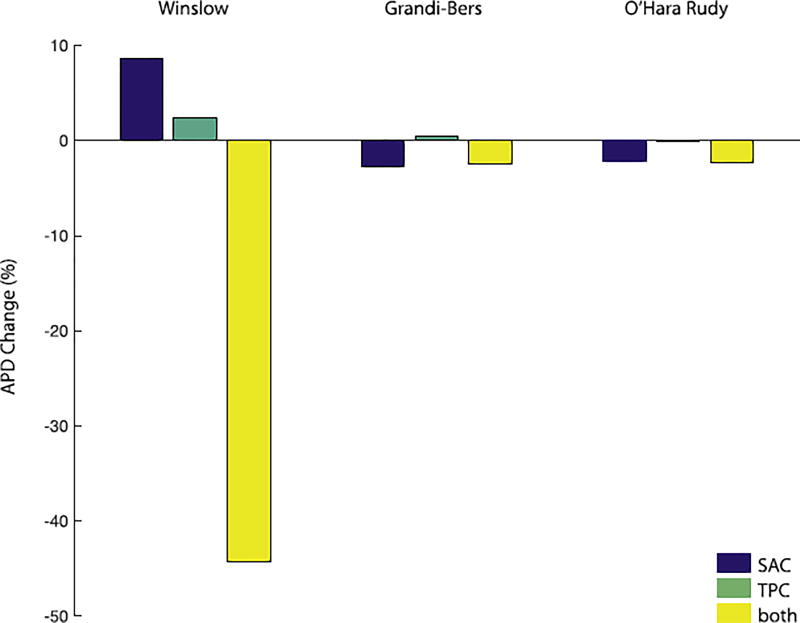
Fig. 3.
Comparison of the APD 90% values and timings between the different models and the individual effects of SAC, TPC, both together, and none. The canine model shows the biggest difference in APD 90% with a shortening of 183ms (44.3%) when both stretch induced calcium release mechanisms are active (yellow bar). However, the shortening of APD 90% are maximal for SAC only with 9ms (2.3%) for the Grandi-Bers model (blue bar) and 10ms (2.7%) for the O'Hara-Rudy model (blue bar).
3.2. Stretch timing only modestly accounts for species differences in MEF
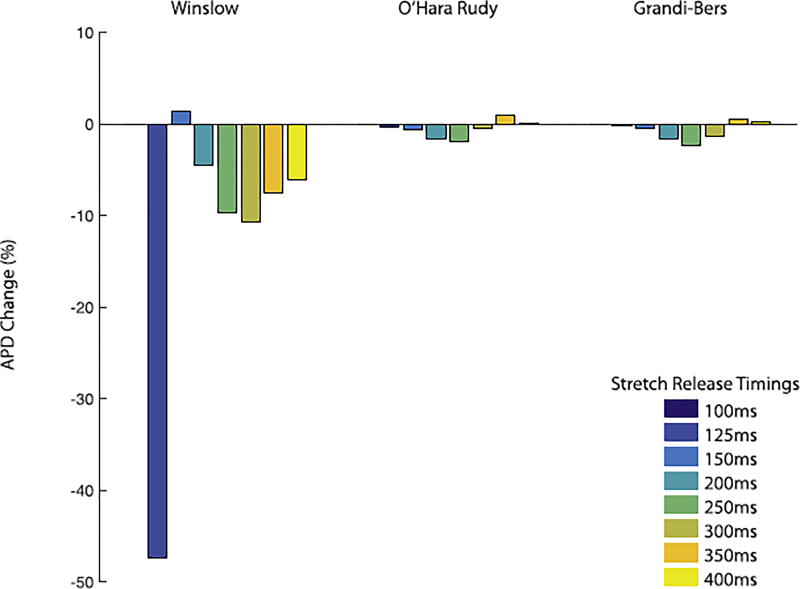
To understand whether the timing of the stretch could account for the species-differences observed in the pre-stretch experiments shown in Fig. 4, we next subjected the models to varying stretch-timing. Simulations with all three strongly-coupled electromechanical models revealed that the shortening of APD depends on the timing of stretch and the stretch pattern (Fig. 6). For all simulations, the release after stretch elicited larger effects on calcium handling and AP morphology than the onset of stretch. Our findings indicate that intracellular calcium increase occurs with a short delay after the stretch as stretch relaxation causes calcium to detach from TnC. This is consistent with the experiments from ter Keurs et al (ter Keurs et al., 2006). and Wakayama et al. (2001), and also justifies that the on-rate, kon, for calcium binding to TnC is stretch dependent. Most importantly for distinguishing the species-differences described above, we observed that both human models were most sensitive to stretch when the peak strain occurred 150ms after the stimulus, whereas the canine model was most sensitive to earlier stretch events (Fig. 5). However, this distinction in timing between species still only accounted for a modest portion of the overall species-sensitivity to stretch, and it is likely that fundamental differences in how the stretch interacts with the EP dynamics explains most of the species-differences shown in Fig. 4.
Fig. 6.
Comparison of the APD 90% values and timings between the different models at different stretch times. The canine model shows the biggest difference in APD 90% with a shortening of 183ms when both stretch induced calcium release mechanisms are active (dark blue bar). However, for both human models the shortening of APD 90% is between 5 to 10ms.
Fig. 5.
The window of stretch timing in the canine model is in the beginning of the AP while the human model is the most sensitive to strain at approximately 150ms after stimulus. Nevertheless the outcomes in the canine model are more exaggerated in the canine model compared to the human at any stretch timing.
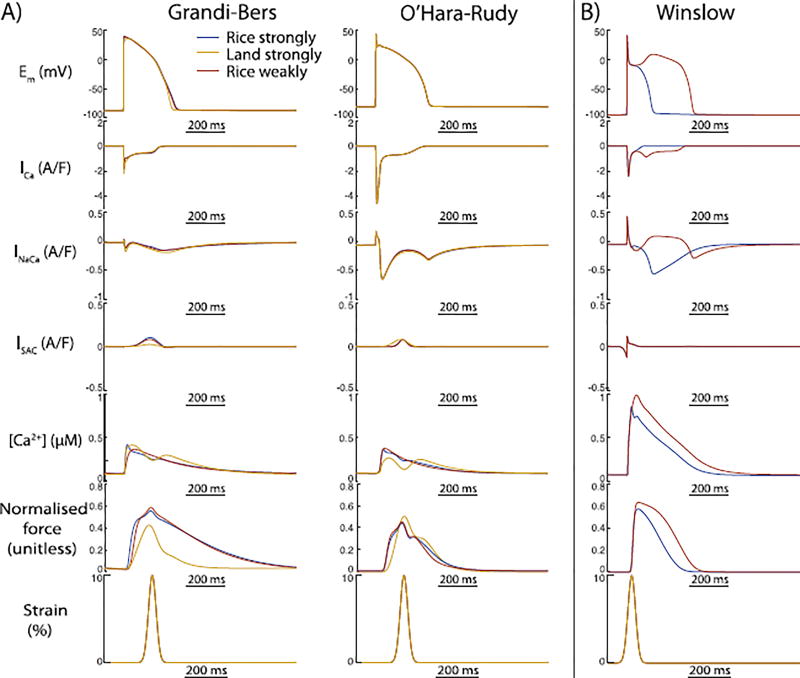
3.3. Humanisation of contraction does not alter MEF in human myocyte models
Because the original Rice contraction model was constructed to replicate rat contraction dynamics and EC coupling, it is possible that differences in the kinetics or steady state calcium-force relationships between rat and human underlie the small AP changes shown in Fig. 4. Hence, to investigate whether the humanisation of the mechanical model alters MEF outcomes, we also coupled both human EP models to a newly released human mechanical model from Land et al. (Land et al., Niederer). Fig. 7 shows that this had a trivial impact on the AP characteristics of either model, and is unlikely to explain differences between the human and animal models. However, to reinforce the importance of using a strongly coupled formulation to allow the calcium binding events at the myofilament to alter the cytosolic calcium in the EP model, we also present simulations in the canine model for which the MEF formulation is weakly coupled. Fig. 7 shows that without the strongly coupled feedback from the myofilaments to the electrophysiolgic model, even the canine AP is relatively insensitive to stretch-induced TPCs. This highlights the central importance of strongly-coupled MEF formulations for permitting stretch-dependent changes in myofilament calcium binding to impact cytosolic calcium concentration, calcium dependent sarcolemmal currents, and MEF outcomes.
Fig. 7.
The outcomes of MEF on EP cannot explain the differences between the human and canine model. (A) Here we show the outcomes of MEF when coupling different mechanical models to the human EP models. We coupled the rat model of Rice et al. reparameterised to replicate human contractile kinetics (humanised, blue line), and the purely human model of Land et al. (yellow line), to both human models. These changes to the mechanical model formulation and parameterisation did not meaningfully alter MEF outcomes. (B) However, MEF is important for the interaction between mechanical changes and EP (red). Here we show the effect of using a weakly coupled formulation of MEF in the canine model, where it completely removes the outcomes of stretch on calcium handling and EP.
3.4. Fibrosis mildly exaggerates the electrophysiologic outcomes of stretch in human myocyte models
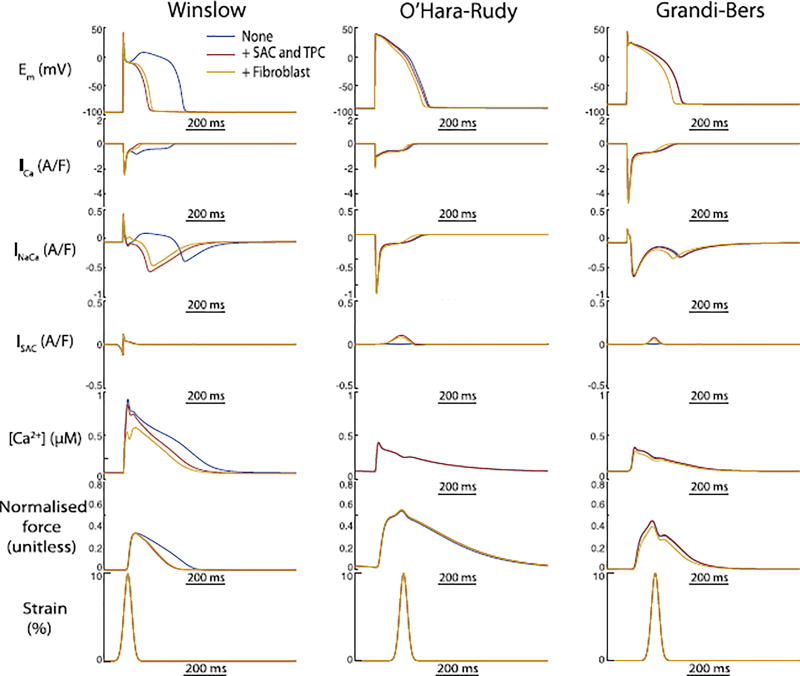
Because arrhythmogenesis associated with stretch is thought to occur in many conditions where substantial cellular and tissue remodelling, particularly fibrosis, has taken place (e.g. post-MI), we next asked whether coupling between myocytes and fibroblasts should be expected to exaggerate or diminish the electrophysiologic outcomes of MEF. Simulations with the coupled electromechanical models including 0.1 fibroblast per myocyte exaggerated the effect of stretch to abbreviate the AP in the human models, albeit modestly (see Fig. 8). In contrast, fibroblast coupling slightly normalised the APD shortening due to stretch in the canine model (Fig. 8, left panels). Thus, these results suggest it is tenable that mild local expansion of the fibroblast population in regions undergoing unusual strain patterns and acute stretch, may contribute slightly to APD shortening and possible arrhythmogenic outcomes.
Fig. 8.
Fibroblast coupling alters MEF-induced changes in AP morphology for all models. In the canine model, fibroblast coupling partially reverses the APD shortening due to stretch alone. In the human models with minimal MEF-induced APD changes, the combined effect of fibroblast coupling and stretch resulted in shortened APD.
3.5. Stress-driven MEF does not alter the electrophysiologic outcomes of acute stretch
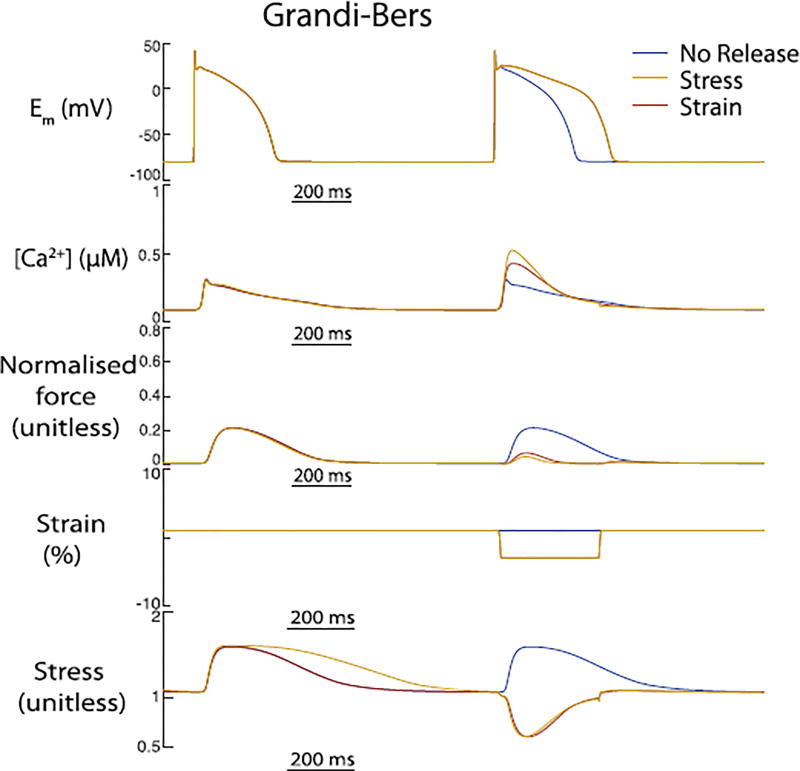
To also incorporate stress in addition to strain, we parameterised our model to the work of Allen et al (Allen and Kurihara, 1980, 1982; Allen and Kentish, 1985). (see Fig. 9). To reach steady state stretch, the cell was pre-stretched from resting length (1.85µm) to Lmax = 1.95µm for 200 beats. Then the stretch was released to 84%Lmax over the whole beat (325ms). As observed by Allen et al., the calcium transient increased by 25% while the active force was significantly reduced. However, the APD of the GrandiBers model showed no change.
Fig. 9.
The differences between stress and strain dependent calcium release from the myofilaments on calcium transient and APD in the Grandi-Bers-Rice model. These results are consistent with the findings of Allen et al (Allen and Kurihara, 1980, 1982; Allen and Kentish, 1985). who showed that after steady state stretch quick release leads to an increase in cytosolic calcium transient and a significant loss in active force.
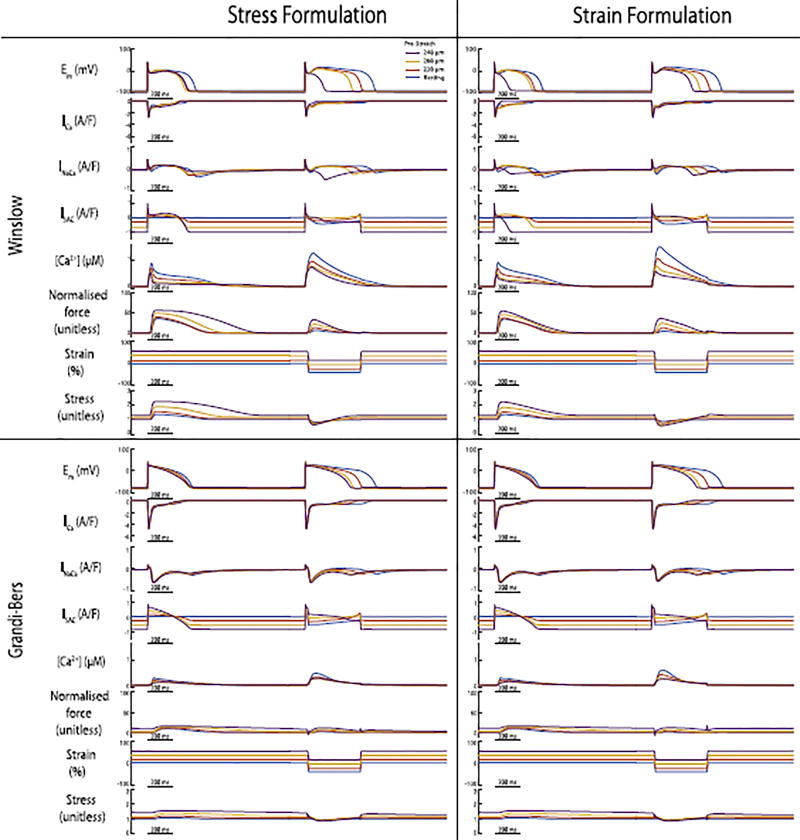
Nonetheless, it is important to notice that the overall outcomes between stress formulation of the model change the force production. Since stress is calculated as a function of force and the cross sectional area of the sarcomere, it creates a direct feedback to force. Therefore, when stretching the sarcomere the twitch dynamics are altered (greater force production). In particular, the same changes in sarcomere length lead to lower forces when stress is considered in our model compared to the strain-based implementation (see Fig. 10). Though force plays an important role for higher dimensional simulations, the impact for these 0D simulations did not change the outcomes of APD or calcium significantly to see a difference between the stress- and strain formulation of the models.
Fig. 10.
The differences between stress and strain dependent calcium release from the myofilaments on calcium transient and APD for both, stress and strain formulations, of the canine and both human models. Steady state stretch prolongs the APD 90% for all models even though stretch release (sarcomere shortening of 0.4µm) leads to even greater prolongations in APD.
3.6. MEF outcomes depend on pre-stretch
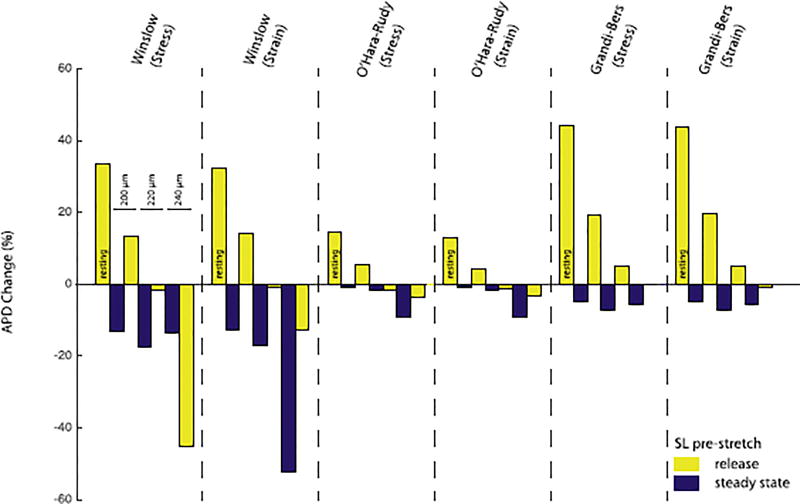
For all models, the degree of pre-stretch was important for the steady state APD as well as the change in APD after release (see Fig. 10). For both, human and canine, we found that steady-state strain alters steady-state APD as well as the APD after releasing the strain. Commonly, the APD for all models prolonged by over 12.5% after releasing the strain; independently of the strain- and stress-formulation. Also, steady state stretch prolonged the APD for all models; though the biggest effect was seen in the canine model with ~ 200ms (see Fig. 10 and Fig. 11). All models show large variations in APD resulting from stretch release. Decreases in myofilament calcium affinity accompanying the sarcomere shortening occur early in the AP plateau and combine with later SAC current to drive AP prolongation in most cases. The longest APD occurs for shortening from resting length and the least prolongation occurs for rapid shortening from maximal sarcomere length(2.4µm). Additionally, the Winslow model does not undergo the same extent of APD shortening in the pre-stretch beat for the stress-dependent MEF formulation compared to the strain-dependent formulation. This is likely due to the subtle difference in timing of the stress-dependent myofilament calcium dissociation and strain-dependent induction of SACs in this model. As shown in Fig. 4 (top left), simultaneous effects of both mechanisms are required for such early repolarisation.
Fig. 11.
Comparison of changes in APD 90% between the stress and strain formulations of the models with different pre-stretches (changes in sarcomere length): from left to right 1.85µm (resting length), 2.0µm, 2.2µm, and 2.4µm; the APD changes for the steady state pre-stretched beat (blue) and release beat (yellow) referenced to an unstretched beat. In the canine model, the difference in APD 90% shortening varies between 220ms (stress-formulation) and 359ms (strain-formulation) when releasing from 2.4µm (steady state) to 2.0µm. Even though all models show significant differences between the different pre-stretches as well as the release after the different pre-stretches, there is little difference between the stress and strain formulation.
4. Discussion
In this study we examined the importance of two different mechanisms of mechano-electric feedback in cardiomyocytes - stretch-activated current induction, and strain-induced myofilament calcium release (also known as triggered propagating contractions). We have assessed the arrhythmogenic potential of each when imposed upon different electrophysiologic backgrounds with known differences in EC-coupling and repolarisation dynamics. Because TPC induction relies on a strongly coupled form of mechano-electric feedback (dynamic stretch-dependent calcium release from the myofilaments), whereas SAC activation relies only upon stretch and electrochemical driving force, we hypothesised that different formulations of myofilament-calcium feedback and different stretch timing would determine the ability of each mechanism to impact the AP. Our simulations support these hypotheses and suggest six key findings regarding mechanisms of cardiac MEF: (1) the importance of SAC and TPC mechanisms to MEF outcomes depends on the electrophysiologic background of the cell, where an exaggerated spike-and-dome AP morphology is much more sensitive to either mechanism; (2) Stretch-timing is a key modulator of MEF outcomes in both canine and human electrophysiologic backgrounds; (3) strongly-coupled formulations for myofilament-cytosol calcium interaction are essential for simulating the role of myofilament calcium dissociation in MEF, but human-specific parameterisation of myofilament calcium-binding kinetics is not; (4) simulated myocyte-fibroblast coupling has different effects on MEF-driven AP changes depending on species; (5) a stress-based formulation for stretch-dependent myofilament calcium sensitivity does not change APD compared to the strain-based formulation, but recapitulates loss of active force more closely as seen in experiments; (6) steady-state strain itself, and particularly release of that steady-state strain, influences APD significantly in all models. In human models, these effects exaggerate the AP changes accompanying MEF. Together these findings highlight the importance of early repolarisation dynamics, the baseline magnitude and kinetics of intracellular calcium cycling, and the specific manner in which dynamic myofilament calcium binding is related to free cytosolic calcium for determining the electrophysiologic impact of MEF.
4.1. Electrophysiologic background and stretch timing determine the outcomes of MEF
We began by examining the electrophysiologic conditions likely to differentiate the role of SACs and TPCs in MEF by assessing the potency of both mechanisms when imposed upon different AP models. We chose two established human epicardial myocyte models to understand whether MEF mechanisms were likely to diverge as a result of known differences in AP plateau dynamics. Briefly, two major differences between the Grandi-Bers and O'Hara- Rudy models lie in the contributions made by forward mode INaCa (inward current), and outward current carried by the rapidly activating delayed rectifier (IKr) to the AP plateau and repolarisation. The Grandi-Bers model exhibits larger inward INaCa, particularly early in the AP plateau, while the O'Hara-Rudy formulation is built upon a much larger outward IKr. These distinctions indicate fundamentally different balance between calcium-dependent (INaCa) and calcium-independent currents during the AP plateau (IKr in O'Hara-Rudy does not incorporate calcium sensitivity). Importantly, however, the two models retain very similar AP waveforms. Thus, any differences between these two models in MEF-induced morphology were expected to indicate the sensitivity of underlying dynamics to the MEF mechanisms, rather than the trajectory of repolarisation. As shown in Figs. 4 and 5, these dynamical differences did little to predispose either human model to repolarisation abnormalities, thus suggesting that the AP trajectory is likely to be more important than the underlying dynamics in determining susceptibility to stretch-induced AP heterogeneity.
To determine whether large differences in the trajectory of the AP plateau could influence MEF sensitivity we used the canine epicardial model of Winslow et al., as an example of a large rodent AP with quite different early repolarisation dynamics. This model differs from both human models in that it incorporates the characteristically large transient outward current (Ito) and spike-and-dome AP morphology present in dog epicardium. Our simulations with this model uncovered two important characteristics of the interaction between the MEF mechanisms and canine electrophysiology. First, under all stretch protocols the canine AP is more sensitive to both MEF mechanisms than either human model (Figs. 4 and 5). Second, in terms of overall repolarisation, the interaction of the SAC and TPC mechanisms are complementary and opposite in direction to either individual effect (Fig. 5). As mentioned above, the large Ito present in the canine epicardium is likely to make a major contribution to the greater MEF sensitivity. It is known that the large Ito in canine epicardium serves to prolong rather than shorten the AP by potentiating voltage-dependent activation of ICaL (Hund and Rudy, 2004). However, it is also clear that sufficiently strong early repolarisation distinguishes the short-lived AP of rodents and longer APs of larger rodents (Grandi et al., 2014; Morotti et al., 2014; Edwards and Louch, 2017), and the large phase 1/2 notch in the canine epicardial AP represents a period in repolarisation where a shift in balance towards outward going currents can sharply abbreviate the AP (Edwards and Louch, 2017). Because both the SAC current and INaCa are small but outward at this critical point, incorporating both of these effects can reach the repolarisation threshold required to prevent the AP dome. For the SAC mechanism this is straightforward, because stretch potentiates this current and the notch membrane potential forces it to be outward. However, the dynamics are more complex for understanding how the TPC mechanism potentiates outward (reverse mode) INaCa at this time. Because the negative-going phase of the stretch (stretch relaxation) is associated with increasing myofilament calcium affinity, relaxation of the pre-stretch shown in Fig. 4 causes the myofilaments to sequester calcium that would otherwise be available for sodium calcium-exchange, thereby promoting reverse-mode function and outward INaCa. Thus, the individual effects of both SACs and TPCs during the notch potentiate the known effect of Ito to prolong the AP, but when combined they are sufficient to provide enough outward current to cause early AP repolarisation.
A potentially important distinction between the canine and human models that we have not examined closely is a large difference in the baseline calcium cycling. The canine model exhibits a calcium transient that rises more rapidly and reaches a peak that is approximately 2.5-fold higher than either human model. This difference would be expected to increase susceptibility to calcium-dependent MEF mechanisms such as TPCs. Prior human models have exhibited more pronounced calcium cycling (Iyer et al., 2004; ten Tusscher and Panfilov, 2006), but to fully reparameterise the calcium cycling of the models used here was beyond the scope of this study. Nonetheless, it would be desirable in the future to understand the importance of these baseline calcium handling characteristics for the balance between TPCs and SACs in MEF.
4.2. Important considerations for calcium-dependent MEF formulations
A critical methodological aspect for distinguishing the role of TPCs and SACs in stretch-induced arrhythmia is to accurately describe the relationship between myofilament calcium binding and free cytosolic calcium. In many studies, formulation of this relationship is weakly coupled (Zile and Trayanova, 2016). That is, time-varying cytosolic calcium concentration calculated by an EC coupling model is provided as input to a model of myofilament dynamics, but the calcium-binding behaviour of the myofilament model is not used to iteratively feedback on the free cytosolic calcium concentration. While such formulations may be reasonable for modelling cyclic calcium-driven contraction, they are not well-suited to modelling the relationship between cytosolic calcium and force during mechanical perturbations. As such, we herein defined strongly-coupled formulations for which the calcium binding dynamics of the contractile models determined the relationship between cytosolic calcium and myofilament behaviour. These formulations more reasonably approach conservation of calcium mass between the EP and myofilament models, and we expected that this would be required to simulate TPCs. As shown in Fig. 7, a weakly-coupled formulation of myofilament dynamics prevents stretch-induced changes in myofilament force from impacting cytosolic calcium, and AP morphology in all models. This demonstrates the importance of this aspect of model formulation for characterising calcium-dependent MEF mechanisms, particularly in the case of an imposed stretch.
4.3. The interaction of diffuse fibrosis and acute stretch in MEF-induced arrhythmogenesis
Unlike previous studies that have observed effects of MEF activation on repolarisation in other myocyte models (de Oliveira et al., 2013; Zile and Trayanova, 2016), we did not observe changes in AP morphology large enough to be considered arrhythmogenic in either human model. In part this may be due to our relatively conservative parameterisation, but it may also be a failure to reflect arrhythmogenic conditions in vivo which are likely to involve a range of additional arrhythmogenic factors, including calcium overload and local tissue fibrosis. To explore this possibility we simulated diffuse fibrosis by coupling our myocyte models to simulated fibroblasts at a ratio of 1 fibroblast per 10 myocytes. The current load imposed by this coupling altered the dynamical changes accompanying stretch in both the human and canine models, albeit not dramatically. Under conditions of more severe fibrosis, and perhaps simultaneous calcium overload, we would speculate that arrhythmogenic outcomes would be exaggerated, but have not tested those conditions in this study.
4.4. Stress-dependent MEF formulations alter dynamic force-calcium interactions but not electrophysiologic outcomes
In this study, we examined stress- and strain-dependent formulations for altering myofilament calcium affinity, which were based on two different experimental data sets (Wakayama et al., 2001; Allen and Kentish, 1985). While the stress formulation is a good approach to achieve a reasonable force-calcium feedback relationship, it results in a reduction of the calcium transient beyond that which is experimentally observed. Conversely, the strain-based formulation retains observed cytosolic calcium dynamics, but cannot capture the reduction in active force production during stretch release experiments. We contend that this supports the importance of both stress and strain dependent mechanisms in mechanoelectric feedback.
4.5. Importance of steady state stretch and release on MEF
In contrast to earlier studies, we considered both transient and steady-state stretch, to examine the short and long term impacts and feedback on APD. As shown in (Fig. 11), steady-state stretch decreases APD in all models. However, stretch-release changes the shape and magnitude of the calcium transient significantly and therefore achieves marked APD variation independent of the choice of the model.
4.6. Limitations
While this study provides a range of new insights to MEF arrhythmogenesis, our approach of course holds some noteworthy limitations. First, we have not explicitly simulated the X-ROS signaling within our models. Because we used whole muscle data for our TPC parameterisation, it is likely that X-ROS-mediated responses are included within those dynamics, however it is not possible for us to separately analyse these dynamics and it is likely that X-ROS is more important than myofilament calcium sensitivity in some contexts, particularly as diastolic stretch (Prosser et al., 2011, 2013).
Another limitation is imposed by the availability of data to parameterise these models for human myocytes. Both SACs and the induced calcium release data that were used to paramaterise our models were developed for animal data and applied to human electrophysiology models. It is possible that these mechanisms occur with much different magnitude in human cells and would therefore have a greater effect. Future work is needed to better characterise these mechanisms in human myocytes.
Furthermore, we imposed stretch with only one strain pattern. We neither carried out simulations on different temporal strain patterns nor did we simulate spatial patterns other than longitudinal strain (e.g. axial or torsional strain). For these questions a 3D spatial model is needed such as that used by Chase et al.’s (Chase et al., 2004) which simulates the 3D structure of thin filament, and hence torsional stresses and changes in thin filament structure due to mechanical deformation can be considered.
We have used different electrophysiologic models and formulations as a means of assessing how SAC and TPC mechanisms interact with different model characteristics. While this approach makes use of validated models that highlight specific characteristics of the physiology, such as a spike-and-dome AP morphology, a more comprehensive and less biased approach to understanding the relationships between MEF mechanisms and model characteristics could be achieved through broader reaching approaches to parameter estimation and sensitivity analyses (Britton et al., 2013; Lee et al., 2013).
Our model computes an isolated cell with normalised forces, strain, and stress. In a realistic geometry, the reparameterisation of the model for the corresponding twitch profile might generate stresses which might not be consistent with in-vivo stresses in papillary muscles.
Finally, TPCs are active contractile events that cannot entirely be captured in a 0D model. Hence, we only investigated the trigger of TPCs but could not investigate or rule out that the calcium transients in both human models would not propagate, create changes in APD, or trigger arrhythmias.
5. Conclusions
This study examines the cellular mechanisms underlying changes of APD due to strain in the presence of stretch-activated currents and stretch-dependent changes in myofilament calcium sensitivity. The goals of this study were to describe which mechanisms contribute most strongly to MEF in realistic mechanical and electrophysiologic conditions. Using strongly coupled electromechanical models of the canine and human epicardial myocytes, we showed that the electrophysiologic outcomes of both MEF mechanisms are crucially dependent on the background electrophysiologic and calcium handling characteristics of the myocyte, the timing of the stretch, and the manner in which calcium couples the myofilaments to the electrophysiologic model. We also found that the effect of remodelling of fibroblasts under pathological conditions is also specific to the background electrophysiologic model and amplifies shortening of APD in human. Together these findings suggest that multiple stretch-activated mechanisms play a role in cardiac MEF and may contribute to arrhythmogenic substrate in pathology.
Acknowledgments
This study has been supported by the Simula-UCSD-University of Oslo Research and PhD training (SUURPh) program, an international collaboration in computational biology and medicine funded by the Norwegian Ministry of Education and Research. The research was also supported by the Center for Cardiological Innovation (203489/O30) as well as NIH grants R01 HL105242, P41 GM103426 (National Biomedical Computation Resource), HL126273, HL137100 to A.D.M.
Footnotes
Conflicts of interest
We also disclose that A.D.M. is a co-founder of and has an equity interest in Insilicomed and Vektor Medical. He serves on the scientific advisory board of Insilicomed and as scientific advisor to both companies. Some of his research grants, including those acknowledged here, have been identified for conflict of interest management based on the overall scope of the project and its potential benefit to these companies. The author is required to disclose this relationship in publications acknowledging the grant support, however the research subject and findings reported here did not involve the company in any way and have no specific relationship with the business activities or scientific interests of either company. The terms of this arrangement have been reviewed and approved by the University of California San Diego in accordance with its conflict of interest policies.
References
- Allen DG, Kentish JC. The cellular basis of the length–tensionrelation in cardiac muscle. J. Mol. Cell Cardiol. 1985;17:821–840. doi: 10.1016/s0022-2828(85)80097-3. [DOI] [PubMed] [Google Scholar]
- Allen DG, Kurihara S. Calcium transients in mammalian ventricular muscle. Eur. Heart. J. 1980;1:5–15. doi: 10.1093/eurheartj/1.suppl_1.5. [DOI] [PubMed] [Google Scholar]
- Allen DG, Kurihara S. The effects of muscle length on intracellular calcium transients in mammalian cardiac muscle. J. Physiology. 1982;327:79–84. doi: 10.1113/jphysiol.1982.sp014221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baudino TA, Carver W, Giles W, Borg T. Cardiac fibroblasts: friend or foe? Am. J. Physiol. Heart Circ. Physiol. 2006;291:H1015–H1026. doi: 10.1152/ajpheart.00023.2006. [DOI] [PubMed] [Google Scholar]
- Britton OJ, Bueno-Orovio A, Ammel KV, Lu HR, Towart R, Gallacher DJ, Rodriguez B. Experimentally calibrated population of models predicts and explains intersubject variability in cardiac cellular electrophysiology. PNAS. 2013;110:E2098–E2105. doi: 10.1073/pnas.1304382110. http://dx.doi.org/10.1073/pnas.1304382110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burstein B, Nattel S. Atrial fibrosis: mechanisms and clinical relevance in atrial fibrillation. J. Am. Coll. Cardiol. 2008;51:802–809. doi: 10.1016/j.jacc.2007.09.064. [DOI] [PubMed] [Google Scholar]
- Cabo C. Modulation of impulse propagation by fibroblasts. Am. J. Physiol. Heart Circ. Physiol. 2008;294:H1992–H1993. doi: 10.1152/ajpheart.00268.2008. [DOI] [PubMed] [Google Scholar]
- Camelliti P, Borg TK, Kohl P. Structural and functional characterization of cardiac fibroblasts. Cardiovasc. Res. 2005;65:40–51. doi: 10.1016/j.cardiores.2004.08.020. [DOI] [PubMed] [Google Scholar]
- Chase PB, MacPherson JM, Daniel TL. A spatially explicit nanomechanical model of the half-sarcomere: myofilament compliance affects ca2+-activation. Ann. Biomed. Eng. 2004;32:1559–1568. doi: 10.1114/b:abme.0000049039.89173.08. [DOI] [PubMed] [Google Scholar]
- de Oliveira BL, Rocha BM, Barra LPS, Toledo EM, Sundnes J, dos Santos RW. Effects of deformation on transmural dispersion of repolarization using in silico models of human left ventricular wedge. Int. J. Numer. Meth. Biomed. Engng. 2013;29:1323–1337. doi: 10.1002/cnm.2570. http://dx.doi.org/10.1002/cnm.2570. [DOI] [PubMed] [Google Scholar]
- Edwards AG, Louch WE. Species-dependent mechanisms of cardiac arrhythmia: a cellular focus. Clin. Med. Insights Cardiol. 2017:1–14. doi: 10.1177/1179546816686061. http://dx.doi.org/10.1177/1179546816686061. [DOI] [PMC free article] [PubMed]
- Franz MR, Cima R, Wang D, Profitt D, Kurz R. Electrophysiological effects of myocardial stretch and mechanical determinants of stretch-activated arrhythmias. Circulation. 1992;86:968–978. doi: 10.1161/01.cir.86.3.968. [DOI] [PubMed] [Google Scholar]
- Grandi E, Pasqualini F, Bers DM. A novel computational model of the human ventricular action potential and ca transient. J. Mol. Cell Cardiol. 2010;48:112–121. doi: 10.1016/j.yjmcc.2009.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grandi E, Edwards AG, Herren AW, Bers DM. Camkii comes of age in cardiac health and disease. Front. Pharmacol. 2014;5:A154. doi: 10.3389/fphar.2014.00154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Healy SN, McCulloch AD. An ionic model of stretch-activated and stretch-modulated currents in rabbit ventricular myocytes. Eur. Soc. Cardiol. 2005;7:S128–S134. doi: 10.1016/j.eupc.2005.03.019. http://dx.doi.org/10.1016/j.eupc.2005.03.019. [DOI] [PubMed] [Google Scholar]
- Hund TJ, Rudy Y. Rate dependence and regulation of action potential and calcium transient in a canine cardiac ventricular cell model. Circulation. 2004;110:3168–3174. doi: 10.1161/01.CIR.0000147231.69595.D3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iyer V, Mazhari R, Winslow RL. A computational model of the human left-ventricular epicardial myocyte. Biophysical. J. 2004;87:1507–1525. doi: 10.1529/biophysj.104.043299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji Y, Gray RA, Fenton FH. Implementation of contraction to electrophysiological ventricular myocyte models, and their quantitative characterization via post-extrasystolic potentiation. PLoS One. 2015;10:e0135699. doi: 10.1371/journal.pone.0135699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohl P, Hunter P, Noble D. Stretch-induced changes in heart rate and rhythm: clinical observations, experiments and mathematical models. Prog. Biophys. Mol. Biol. 1999;71:91–138. doi: 10.1016/s0079-6107(98)00038-8. [DOI] [PubMed] [Google Scholar]
- Kohl P, Nesbitt AD, Cooper PJ, Lei M. Sudden cardiac death by commotio cordis: role of mechanoelectric feedback. Cardiovasc Res. 2001;50:280–289. doi: 10.1016/s0008-6363(01)00194-8. https://doi.org/10.1016/S0008-6363(01)00194-8. [DOI] [PubMed] [Google Scholar]
- Kohl P, Camelliti P, Burton FL, Smith GL. Electrical coupling of fibroblasts and myocytes: relevance for cardiac propagation. J. Electrocardiol. 2005;38:45–50. doi: 10.1016/j.jelectrocard.2005.06.096. [DOI] [PubMed] [Google Scholar]
- Kohl P, Bollensdorff C, Gamy A. Effect of mechanosensitive ion channels on ventricular electrophysiology: experimental and theoretical models. Exp. Physiol. 2006;91:307–321. doi: 10.1113/expphysiol.2005.031062. [DOI] [PubMed] [Google Scholar]
- Lab MJ. Contraction-excitation feedback in myocardium: physiological basis and clinical relevance. Circulation Res. 1982;50:757–766. doi: 10.1161/01.res.50.6.757. [DOI] [PubMed] [Google Scholar]
- Lab MJ. Mechanosensitive-mediated interaction, integration and cardiac control. Ann. N. Y. Acad. Sci. 2006;1080:282–300. doi: 10.1196/annals.1380.022. [DOI] [PubMed] [Google Scholar]
- Land S, Park-Holohan S-J, Smith NP, dos Remedios CG, Kentish JC, Niederer SA. A model of cardiac contraction based on novel measurements of tension development in human cardiomyocytes. J. Mol. Cell Cardiol. 2017;106:68–83. doi: 10.1016/j.yjmcc.2017.03.008. [DOI] [PubMed] [Google Scholar]
- Lee Y-S, Liu OZ, Hwang HS, Knollmann BC, Sobie EA. Parameter sensitivity analysis of stochastic models provides insights into cardiac calcium sparks. Biophysical. J. 2013;104:1142–1150. doi: 10.1016/j.bpj.2012.12.055. http://dx.doi.org/10.1016/j.bpj.2012.12.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacCannell KA, Bazzazi H, Chilton L, Shibukawa Y, Clark RB, Giles WR. A mathematical model of electrotonic interactions between ventricular myocytes and fibroblasts. Biophysical. J. 2007;92:4121–4132. doi: 10.1529/biophysj.106.101410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maleckar MM, Greenstein JL, Trayanova NA, Giles WR. Mathematical simulations of ligand-gated and cell-type specific effects on the action potential of human atrium. Prog. Biophys. Mol. Biol. 2008;98:161–170. doi: 10.1016/j.pbiomolbio.2009.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maleckar MM, Greenstein JL, Giles WR, Trayanova NA. Electrotonic coupling between human atrial myocytes and fibroblasts alters myocyte excitability and repolarization. Biophys. J. 2009;97:2179–Ð2190. doi: 10.1016/j.bpj.2009.07.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDowell KS, A HJ, Maleckar, Mary M, Trayanova, Natalia A. Susceptibility to arrhythmia in the infarcted heart depends on myofibroblast density. Biophysical J. 2011;101:1307–1315. doi: 10.1016/j.bpj.2011.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miura M, Nishio T, Hattori T, Murai N, Stuyvers BD, Shindoh C, Boyden PA. Effect of nonuniform muscle contraction on sustainability and frequency of triggered arrhythmias in rat cardiac muscle. Circulation. 2010;121(25):2711–2717. doi: 10.1161/CIRCULATIONAHA.109.907717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morotti S, Edwards AG, Mcculloch AD, Bers DM, Grandi E. A novel computational model of mouse myocyte electrophysiology to assess the synergy between Na+ loading and CaMKII. J. Physiology. 2014;592(6):1181–1197. doi: 10.1113/jphysiol.2013.266676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mulieri LA, Hasenfuss G, Leavitt B, Allen PD, Alpert NR. Altered myocardial force-frequency relation in human heart failure. Circulation. 1992;85:1743–1750. doi: 10.1161/01.cir.85.5.1743. [DOI] [PubMed] [Google Scholar]
- OHara T, Virg L, Varr A, Rudy Y. Simulation of the undiseased human cardiac ventricular action potential: model formulation and experimental validation. PLoS Comput. Biol. 2011;7:e1002061. doi: 10.1371/journal.pcbi.1002061. http://dx.doi.org/10.1371/journal.pcbi.1002061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pieske B, Sutterlin M, Schmidt-Schweda S, Minami K, Meyer M, Olschewski M, Holubarsch C, Just H, Hasenfuss G. Diminished post-rest potentiation of contractile force in human dilated cardiomyopathy. functional evidence for alterations in intracellular ca2+ handling. J. Clin. Invest. 1996;98:764–776. doi: 10.1172/JCI118849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prosser BL, Ward CW, Lederer W. X-ros signaling: rapid mechano-chemo transduction in heart. Science. 2011;333:1440–1445. doi: 10.1126/science.1202768. http://dx.doi.org/10.1126/science.1202768. [DOI] [PubMed] [Google Scholar]
- Prosser BL, Khairallah RJ, Ziman AP, Ward CW, Lederer W. X-ros signaling in the heart and skeletal muscle: stretch-dependent local ros regulates [ca2+]i. J. Mol. Cell. Cardiol. 2013;58:172–181. doi: 10.1016/j.yjmcc.2012.11.011. http://dx.doi.org/10.1016/j.yjmcc.2012.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice JJ, Wang F, Bers DM, de Tombe PP. Approximate model of cooperative activation and crossbridge cycling in cardiac muscle using ordinary differential equations. Biophysical J. 2008;95:2368–2390. doi: 10.1529/biophysj.107.119487. http://dx.doi.org/10.1529/biophysj.107.119487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruwhof C, van Wamel JET, Noordzij LAW, Aydin S, Harper JCR, van der Laarse A. Mechanical stress stimulates phospholipase c activity and intracellular calcium ion levels in neonatal rat cardiomyocytes. Cell Calcium. 2001;29:73–83. doi: 10.1054/ceca.2000.0158. http://dx.doi.org/10.1054/ceca.2000.0158. [DOI] [PubMed] [Google Scholar]
- Sachs F, Sigurdson W, Ruknudin A, Bowman C. Single-channel mechanosensitive currents. Science. 1991;16(253):800–801. doi: 10.1126/science.253.5021.800-a. (5021) [DOI] [PubMed] [Google Scholar]
- Taggart P, Labb M. Cardiac mechano-electric feedback and electrical restitution in humans. Prog. Biophys. Mol. Biol. 2008;97:452–460. doi: 10.1016/j.pbiomolbio.2008.02.021. [DOI] [PubMed] [Google Scholar]
- Taggart P, Sutton PM, Treasure T, Lab M, OBrien W, Runnalls M, Swanton RH, Emanuel RW. Monophasic action potentials at discontinuation of cardiopulmonary bypass: evidence for contraction-excitation feedback in man. Circulation. 1988;77:1266–1275. doi: 10.1161/01.cir.77.6.1266. [DOI] [PubMed] [Google Scholar]
- Ten Tusscher K, Panfilov A. Cell model for efficient simulation of wave propagation in human ventricular tissue under normal and pathological conditions. Phys. Med. Biol. 2006;51(23):6141. doi: 10.1088/0031-9155/51/23/014. [DOI] [PubMed] [Google Scholar]
- ten Tusscher KHWJ, Panfilov AV. Alternans and spiral breakup in a human ventricular tissue model. AJP Heart. 2006;291:H1088–H1100. doi: 10.1152/ajpheart.00109.2006. http://dx.doi.org/10.1152/ajpheart.00109.2006. [DOI] [PubMed] [Google Scholar]
- Ten Tusscher K, Noble D, Noble P, Panfilov AV. A model for human ventricular tissue. Am. J. Physiology-Heart Circulatory Physiology. 2004;286(4):H1573–H1589. doi: 10.1152/ajpheart.00794.2003. [DOI] [PubMed] [Google Scholar]
- ter Keurs HE, Zhang YM, Miura M. Damage-induced arrhythmias: reversal of excitationÐcontraction coupling. Cardiovasc Res. 1998;40:444–455. doi: 10.1016/s0008-6363(98)00263-6. [DOI] [PubMed] [Google Scholar]
- ter Keurs HE, Wakayama Y, Miura M, Shinozaki T, Stuyvers BD, Boyden PA, Landesberg A. Arrhythmogenic ca2+ release from cardiac myofilaments. Prog. Biophysics Mol. Biol. 2006;90:151–171. doi: 10.1016/j.pbiomolbio.2005.07.002. http://dx.doi.org/10.1016/j.pbiomolbio.2005.07.002. [DOI] [PubMed] [Google Scholar]
- Trayanova NA, Rice JJ. Cardiac electromechanical models: from cell to organ. Front. Physiology. 2011;2(43):1–19. doi: 10.3389/fphys.2011.00043. http://dx.doi.org/10.3389/fphys.2011.00043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakayama Y, Miura M, Sugai Y, Kagaya Y, Watanabe J, ter Keurs HEDJ, Shirato K. Stretch and quick release of rat cardiac trabeculae accelerates ca2+ waves and triggered propagated contractions. Am J Phys. 2001;281:H2133–H2142. doi: 10.1152/ajpheart.2001.281.5.H2133. [DOI] [PubMed] [Google Scholar]
- Wakayama Y, Miura M, Stuyvers BD, Boyden PA, ter Keurs HE. Spatial nonuniformity of excitation contraction coupling causes arrhythmogenic ca2+ waves in rat cardiac muscle. Circulation Res. 2005;96:1266–1273. doi: 10.1161/01.RES.0000172544.56818.54. http://dx.doi.org/10.1161/01.RES.0000172544.56818.54. [DOI] [PubMed] [Google Scholar]
- Winslow RL, Rice J, Jafri S, Marbn E, ORourke B. Mechanisms of altered excitation-contraction coupling in canine tachycardia-induced heart failure, ii model studies. Circulation Res. 1999;84:571–586. doi: 10.1161/01.res.84.5.571. http://dx.doi.org/10.1161/01.RES.84.5.571. [DOI] [PubMed] [Google Scholar]
- Yaniv Y, Juhaszova M, Wang S, Fishbein KW, Zorov DB, J Sollott S. Analysis of mitochondrial 3d-deformation in cardiomyocytes during active contraction reveals passive structural anisotropy of orthogonal short axes. PLoS One. 2011;6:e21985. doi: 10.1371/journal.pone.0021985. http://dx.doi.org/10.1371/journal.pone.0021985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zabel M, Koller B, Sachs F, Franz M. Stretch- induced voltage changes in the isolated beating heart: importance of the timing of stretch and implications for stretch-activated ion channels. Cardiovasc. Res. 1996;32:120–130. [PubMed] [Google Scholar]
- Zile MA, Trayanova NA. Rate-dependent force, intracellular calcium, and action potential voltage alternans are modulated by sarcomere length and heart failure induced-remodeling of thin filament regulation in human heart failure: a myocyte modeling study. Prog. Biophys. Mol. Biol. 2016;120:270–280. doi: 10.1016/j.pbiomolbio.2015.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]