Abstract
A prevalent view of visual working memory (VWM) is that visual information is actively maintained in the form of perceptually integrated objects. Such reliance on object-based representations would predict that after an object is fully encoded into VWM, all features of that object would need to be maintained as a coherent unit. Here, we evaluated this idea by testing whether memory resources can be redeployed to a specific feature of an object already stored in VWM. We found that observers can utilize a retrospective cue presented during the maintenance period to attenuate both the gradual deterioration and complete loss of memory for a cued feature over time, but at the cost of accelerated loss of information regarding the uncued feature. Our findings demonstrate that object representations held within VWM can be decomposed into individual features and that having to retain additional features imposes greater demands on active maintenance processes.
Keywords: short-term memory, visual attention, visual memory, open data
Most objects that people encounter in everyday life possess numerous visual attributes, such as color, shape, texture, and location. These elementary visual attributes are integrated by the visual system, giving rise to the conscious percept of a coherent object (Treisman, 1996). There is broad agreement that perceptual objects play a special role in visual cognition. Multiple visual features can be perceived without mutual interference when they are conjoined into a single object (Blaser, Pylyshyn, & Holcombe, 2000; Duncan, 1984). Moreover, attending to one feature of an object can automatically enhance the processing of the other features of the same object (O’Craven, Downing, & Kanwisher, 1999). It is widely believed that perceptual objects also constitute the fundamental format for representing visual information in visual working memory (VWM; Irwin & Andrews, 1996; Luck & Vogel, 1997).
The object-based nature of VWM representations is supported by the finding that the capacity of VWM appears limited by the number of objects and not the number of features. In a seminal study, Luck and Vogel (1997) found that change-detection performance systematically declined as the number of to-be-remembered objects increased beyond four items, but the number of task-relevant features present in each object had no detrimental cost. For example, four objects defined by color and orientation (i.e., eight features total) could be remembered just as accurately as four objects defined by either feature alone. These findings led to the integrated-object hypothesis, which posits that VWM consists of a small, fixed number of slots, each of which can effectively store all of the features of an object in an integrated format (Luck & Vogel, 1997). Although it has been debated whether the storage of multifeature objects is entirely cost free (e.g., Cowan, Blume, & Saults, 2013; Fougnie, Asplund, & Marois, 2010; Oberauer & Eichenberger, 2013), it is generally agreed that multiple independent features are stored much more efficiently when they form a unitary object (Delvenne & Bruyer, 2004; Olson & Jiang, 2002; Wheeler & Treisman, 2002; Xu, 2002).
Even if VWM can efficiently store multiple features of an object, the initial encoding process can be biased by feature-selective attention. Focusing attention on a single, task-relevant feature dimension can speed its rate of encoding (Woodman & Vogel, 2008) and enhance the representational precision of that feature in VWM (Fougnie et al., 2010). These findings indicate that the features of an object can be unbound and separately processed at the initial encoding stage of VWM, allowing for the prioritization of task-relevant information. However, it is unknown whether the features of an already encoded object can be readily unbound during the maintenance stage of VWM.
Our study had two goals. First, we wanted to test a strong prediction of the integrated-object hypothesis, namely that all features of an encoded object are obligatorily bound together in VWM. Specifically, we wanted to determine whether it is possible to reprioritize a specific feature of an object after all features of that object have been encoded in VWM. We relied on retrospective cuing (see Souza & Oberauer, 2016, for a review) of a task-relevant feature dimension, such that all features of the object had to be initially encoded with equal priority. Retrospective prioritization of a feature should be possible if VWM representations of objects can be decomposed into their component features, but not if those features are obligatorily maintained as an integrated unit.
Should retrospective cuing reveal a feature-selective benefit, our second goal was to determine the source of this benefit. If all of the available information about the object consists of what is currently maintained in VWM, then focusing greater resources on a particular feature of a maintained object could not possibly lead to an improvement in that feature representation, beyond its current state. However, if information in VWM tends to suffer from deterioration or probabilistic forgetting over time, a shift of attentional resources to a particular feature could serve to attenuate the rate of information loss, which would lead to a cuing benefit following a delay. Recent studies suggest that information in VWM can be lost within a few seconds, especially when multiple objects have to be maintained (Zhang & Luck, 2009), and that information loss can be attenuated for a retrospectively cued object (Pertzov, Bays, Joseph, & Husain, 2013; Williams, Hong, Kang, Carlisle, & Woodman, 2013). In the present study, we evaluated the temporal stability of VWM for objects defined by color and orientation, retrospectively cuing either feature dimension after these objects were encoded into VWM. A particular feature of an object was tested afterward using a continuous report paradigm (Wilken & Ma, 2004) to separately estimate the number of successfully maintained features and the precision of these representations (Zhang & Luck, 2008). We show that retrospective cues lead to superior memory precision and decreased likelihood of forgetting for validly cued features (Experiments 1 and 2), because such reprioritization can effectively attenuate the rate of information loss in VWM (Experiment 3).
Experiment 1
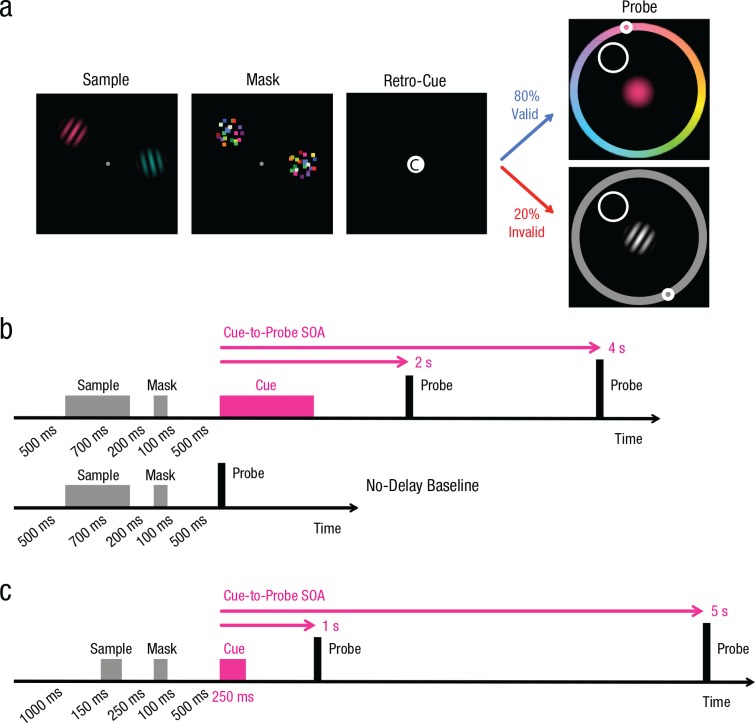
Valid, neutral, and invalid retrospective cues (retro-cues) were tested in Experiment 1 to assess the benefits and costs of prioritizing a particular feature of an encoded object. On each trial, two objects defined by color and orientation were briefly presented, followed by a patterned mask and then a retro-cue indicating which feature dimension would likely be tested (see Fig. 1). To examine how the retro-cue might influence the rate of information loss over time, we also manipulated the delay duration between the retro-cue and the subsequent probe.
Fig. 1.
Example displays and trial sequences from Experiments 1 through 3. In all experiments, participants saw a sample array containing two gratings (a) and were asked to attend to both the color and orientation of the gratings. After the presentation of a patterned mask, participants saw either an informative feature cue (“C” for color, “O” for orientation) indicating which feature dimension was most likely to be probed or a neutral cue (“E”) indicating that either color or orientation would be tested with equal likelihood. The feature cues were 80% valid in Experiment 1 and 100% valid in Experiments 2 and 3. The diagram in (b) shows the sequence of events for cue trials (top) and for no-delay trials (bottom) in Experiment 1. On cue trials, one of the three cues (“C,” “O,” or “E”) appeared after the mask array. To evaluate whether the retro-cue influenced the rate of information loss over time, we manipulated the stimulus-onset asynchrony (SOA) between retro-cue and probe. On no-delay baseline trials (7.0% of all trials), the color or orientation probe appeared 500 ms after the mask array. The diagram in (c) shows the sequence of trial events in Experiment 3, in which we evaluated the effects of valid and neutral cues using a wider range of delay durations.
Method
Participants
Twenty volunteers (5 male, 15 female; age: 18–33 years) with normal color vision and visual acuity completed the experiment for course credit or monetary compensation. The sample size was determined on the basis of the data from a pilot study (N = 16), which tested VWM at a delay of 2 s following the retro-cue onset. We examined effect sizes of cuing on memory precision and retention rates. Using paired-samples t tests with a two-tailed alpha of .05, we estimated that detection of cuing benefits on memory precision and retention rates (Cohen’s ds = 1.00 and 0.83) would require sample sizes of 11 and 14, respectively, to achieve 80% power, while detection of a cuing cost on retention rates (Cohen’s d = 0.45) would require a sample size of 40. We decided that an intermediate sample size of 20 would be sufficient to detect both cuing benefits and costs in Experiment 1, on the basis of the hypothesis that a longer delay of 4 s should lead to a greater loss for deprioritized features, thereby producing stronger cuing costs. One participant performed extremely poorly on the catch trials (see the Procedure for more details), which indicated an inability to perform the task or a lack of compliance, and was excluded from further analysis. The final data set consisted of 19 participants. The study was conducted according to procedures approved by the Vanderbilt University Institutional Review Board.
Apparatus
The experiment was conducted using MATLAB 7.5 (The MathWorks, Natick, MA) and the Psychophysics Toolbox extensions (Brainard, 1997). Stimuli were presented on a 20-in. CRT monitor (1,152 × 870 resolution, 75 Hz refresh rate) at a viewing distance of 57 cm. Participants’ heads were stabilized by a chin rest. The monitor was carefully calibrated for precise color and luminance presentation. The calibration data included the spectral distribution of all red, green, and blue phosphors at maximum intensity (measured with a USB4000 spectrometer; Ocean Optics, Winter Park, FL), as well as calibration of the gamma function of each channel (measured with a Minolta LS-110 luminance meter). We used a commercially available control knob (PowerMate USB multimedia controller, Griffin Technology, Nashville, TN) to allow participants to continuously adjust the feature values.
Stimuli
Sample arrays consisted of two sine-wave gratings (2.4° diameter, spatial frequency = 1.67 cycles per degree) that varied randomly in color and orientation. Colored gratings appeared within a circular two-dimensional Gaussian envelope (σ = 1.2°) at randomly determined locations 3.6° from a central fixation point, with a minimum of 0.6° separation. Stimulus colors were defined in terms of Commission Internationale de l’Éclairage (CIE) L*a*b* coordinates, which were converted to device-dependent RGB values through a color-luminance calibration procedure. Gratings were generated using 360 colors that were evenly spaced on a circle in CIE L*a*b* color space (centered at L* = 67, a* = 0, b* = 0, with a radius of 50) and 180 evenly spaced orientations (0–180°).
Colored gratings were generated as follows. First, a sine-wave grating pattern was defined in terms of L* (lightness), which fluctuated between 13.2 and 67 units. Each of the 360 colors was then applied to this template pattern. On each colored grating, saturation was linearly adjusted according to L*, such that the brightest parts of the grating (L* = 67) contained the most vivid color (radius = 50), while the darkest parts (L* = 13.2) contained achromatic dark gray (radius = 0). Finally, these gratings were rotated to varying degrees to produce stimuli that varied in both color and orientation. Gratings were presented on a dark gray background (L* = 13.2, a* = 0, b* = 0), which matched the darkest, achromatic portions of the gratings.
Each patterned mask consisted of 40 small colored squares (0.24° × 0.24°) scattered across a circular field that matched the size of one of the gratings in the sample array. The colors and positions of the squares were randomly generated to make new masks on every trial.
Procedure
There were three different classes of trials: cue trials, no-delay trials, and catch trials. Cue trials contained three cue types—valid, neutral, or invalid—with cue-to-probe stimulus-onset asynchronies (SOAs) of either 2 or 4 s. The sequence of events for cue and no-delay trials is shown in Figure 1b. Each trial began with the appearance of a small central fixation point (0.24° × 0.24°) for 500 ms; participants were asked to maintain fixation until the response probe appeared. A sample array consisting of two colored gratings was presented for 700 ms. Color and orientation values were pseudorandomly selected on each trial, independently for each grating. To ensure that feature values were evenly distributed across the respective feature space, we divided each feature space into 10 evenly spaced bins and randomly sampled within each bin to ensure a balanced number of features from each bin across conditions. After a 200-ms delay, a patterned mask was presented for 100 ms to minimize the possibility of relying on high-capacity sensory storage (Phillips, 1974).
On cue trials, a retro-cue appeared in the center of the screen 500 ms after mask offset. This cue consisted of a black letter inside a white circle indicating with 80% validity that color (“C”) or orientation (“O”) would be tested or, in the case of a neutral cue (“E”), that either feature would be tested with equal likelihood. Participants were informed of these probabilities in advance and were encouraged to use the predictive cues to perform the task as well as possible. The cue remained on the screen for 1 s, followed by an additional blank interval (retention period) of 1 or 3 s, which resulted in a cue-to-probe SOA of 2 or 4 s.
The probe display consisted of an outline of a circle indicating the location of the to-be-reported object (500 ms), followed by either a color wheel or an achromatic gray wheel (radius = 7.2°, width = 0.48°) indicating which feature of that object should be reported. The feature values associated with the orientation/color wheel were randomly rotated on every trial, and the starting marker position was also randomized to avoid possible bias. Participants rotated a response knob to move the marker to the appropriate position on the response wheel, which instantaneously updated the color or orientation of a probe stimulus shown at fixation. Participants were asked to replicate the remembered feature value as accurately as possible and subsequently received visual and auditory feedback on every trial during a 1-s intertrial interval.
Visual feedback consisted of a test stimulus (a color patch or monochromatic grating) showing the true feature value, along with a normalized accuracy score (0–100). The accuracy score was calculated as 100% minus the percentage of the absolute error magnitude, relative to the maximum possible error for a given feature space (180° for color, 90° for orientation). Auditory feedback depended on the accuracy score: a pleasant rising tone (≥ 90%), a cash register sound (50–89.99%), or a low-pitched beep (< 50%). For accuracy scores above 90%, participants received 100 bonus points. At the end of each experimental block, the average accuracy and earned bonus points for the block were displayed. Participants generally reported that they found the feedback to be motivating and engaging.
No-delay trials were identical to cue trials, except that the mask array was followed directly by the probe rather than a retro-cue (Fig. 1b). The purpose of this condition was to provide a baseline measure of the amount of information accessible at the time of cue onset, before any modulation by the retro-cue could occur. Similar to the neutral-cue condition, the no-delay condition measured VWM performance after working memory resources had been spread across both feature dimensions, but at a shorter delay. The interstimulus interval between mask and probe was 0.5 s for no-delay trials and either 2.5 or 4.5 s for cue trials.
Given that the informative feature cue (“C” or “O”) was invalid on 20% of the trials, we were concerned that participants might simply ignore the cues. To incentivize participants to actively attend to the cue meaning, we included a small number of intermixed catch trials (24 of 284 trials per session) that required reporting which cue was presented (“C,” “O,” or “E”) instead of responding to a probe display. After removing the outlier participant (accuracy = 63.2%; > 2.5 SD below the group mean), we found that the mean catch-trial accuracy (n = 19) was 88.6% (SD = 6.9%), which indicates reliable processing of the retro-cue.
Each session consisted of 284 trials divided into 10 blocks of 28 or 29 trials each. A short break was provided between blocks. Each participant completed six 1-hr sessions for a total of 1,704 trials. This resulted in 240 valid-, 60 invalid-, and 60 neutral-cue trials for each feature dimension (color and orientation) and each cue-to-probe SOA condition (2 and 4 s), yielding a total of 1,440 cue trials (84.5% of all trials). We also obtained 120 no-delay trials (7.0%), as well as 144 catch trials (72 trials per SOA condition; 8.5%). All trial types were randomly intermixed within a session.
Data analysis
We analyzed the orientation and color-report data using a mixture-model analysis (Zhang & Luck, 2008). The model is based on the assumption that the distribution of response errors should reflect a mixture of two components: a von Mises distribution (the circular analogue of the Gaussian distribution) centered on the true feature value for trials in which the probed feature was successfully held in memory and a uniform distribution for trials in which the probed feature was unavailable for report and a random guess was made. The model has two parameters: standard deviation (SD) and pfailure. The spread of the von Mises distribution is determined by the SD parameter, which is inversely proportional to the precision of the stored representation. The proportional area of the uniform component is determined by pfailure, which represents the probability that the probed feature was lost from memory.
The mixture model was fitted separately to each feature, cue type, and SOA condition for each participant, using maximum-likelihood estimation. A representative participant’s response-error histograms and best-fitting mixture distributions are presented in Figure S1 in the Supplemental Material available online. Figure S2 in the Supplemental Material shows the response-error histograms pooled across all participants. For mixture-model fitting, the color and orientation data were converted from their original feature space (0–360° and 0–180°, respectively) to a circular space that ranged from 0 to 2π radians. This entailed doubling the orientation values (0–180°) to span the full circular space (0–2π radians). This facilitated direct comparison of memory precision across features, regardless of those features’ original spaces. To rule out the possibility that any systematic effect of cue type might be due to the unequal number of trials across the conditions (i.e., 240 valid-cue trials, 60 invalid-cue trials, and 60 neutral-cue trials), we randomly resampled 60 valid-cue trials (with replacement) 2,000 times, fitting the mixture model to each resampled data set. The fitted SD and pfailure parameters for the 2,000 samples were then averaged, and subsequent analyses were conducted using the averaged bootstrapped estimates. Moreover, there was no qualitative difference in the pattern of results when the mixture model was fitted to the original 240 trials in valid cue conditions without bootstrapping.
To evaluate the general effects of cuing benefits and costs, we pooled SD and pfailure estimates across color and orientation. Any differences between color and orientation in terms of the overall memory precision and failure rate, or the effects of cuing and delay duration, will be noted where appropriate.
Results
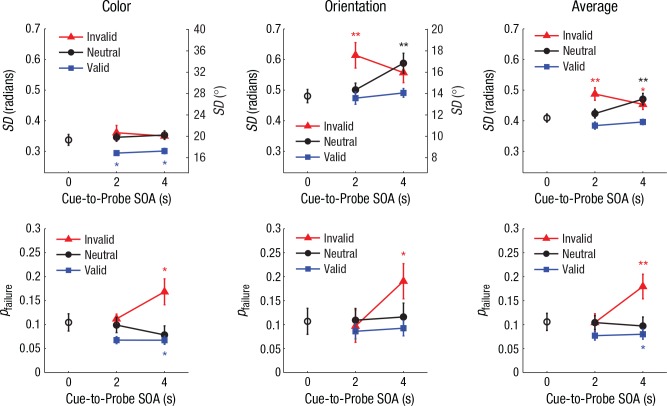
The precision of working memory was generally better for validly cued features than for features reported following a neutral or invalid cue (Fig. 2, top row), as indicated by estimates of SD for delays of 2 and 4 s. We performed a repeated measures analysis of variance (ANOVA) with cue type (valid, invalid, vs. neutral), reported feature (color vs. orientation), and SOA (2 s vs. 4 s) as within-subjects factors. We observed a general precision advantage for color over orientation when considered in radian units in the full circular space (0 to 2π), F(1, 18) = 105.66, p < .001, ηp2 = .85. More importantly, we observed a significant main effect of cue type on memory precision, F(2, 36) = 15.75, p < .001, ηp2 = .47, with no evidence of an interaction between cue type and feature, F(2, 36) = 1.21, p > .250, ηp2 = .06. Thus, the retro-cue had a similar influence on the precision of working memory for both color and orientation, and the average plots illustrate these general effects of cuing.
Fig. 2.
Mixture-model estimates of standard deviation (SD; top row) and probability of memory failure (pfailure; bottom row) for Experiment 1 (n = 19), separately for color, orientation, and average performance across both features. Results for each model are shown as a function of cue-to-probe stimulus onset asynchrony (SOA) and cue type. For both SD and pfailure, higher values on the left y-axes represent poorer working memory performance. The SD values for color and orientation were plotted on the same scale after conversion to a common circular space (0–2π radians); the corresponding degree values for each feature are shown on the right y-axes. The open circles plotted at 0-s SOA show the results from no-delay trials, when there was no retrospective cue (retro-cue). The color-coded asterisks denote significant differences between the no-delay baseline condition and individual retro-cue conditions (*p < .05, **p < .01, based on two-tailed paired-samples t tests). Error bars represent ±1 SEM.
A separate analysis of the averaged SD data indicated a significant precision advantage for validly cued features relative to neutrally cued features, F(1, 18) = 27.78, p < .001, ηp2 = .61, as well as a significant effect of SOA, F(1, 18) = 9.38, p = .007, ηp2 = .34. Whereas memory precision for the validly cued features did not significantly change between 2 and 4 s, t(18) = 1.80, p = .088, Cohen’s d = 0.41, a significant deterioration occurred during this interval for the neutrally cued features, t(18) = 2.73, p = .014, Cohen’s d = 0.63. However, the interaction between cue type (valid vs. neutral) and SOA on SD did not reach significance, F(1, 18) = 4.01, p = .061, ηp2 = .18; we will revisit this issue in Experiment 3.
We also observed a significant cost in memory precision following invalid as compared with neutral retro-cues at 2 s, t(18) = 3.34, p = .004, Cohen’s d = 0.77, though not at 4 s, t(18) = 0.75, p > .250. A significant interaction between invalid and neutral cue type and SOA on SD, F(1, 18) = 9.79, p = .006, ηp2 = .35, indicated that invalidly cued features underwent greater deterioration than neutrally cued features within 2 s after the cue, without a further loss of precision between 2 and 4 s, t(18) = 1.68, p = .111.
The probability of memory failure was also strongly influenced by the retro-cue (Fig. 2, bottom row), with lower rates of failure on valid trials than neutral trials and a prominent trend of greater failure on invalid trials when participants were tested after a prolonged retention period of 4 s. This trend was supported by the ANOVA on memory-failure rates, which indicated a significant effect of cue type, F(2, 36) = 11.79, p < .001, ηp2 = .40, and a significant interaction between SOA and cue type, F(2, 36) = 9.89, p < .001, ηp2 = .35. Analyses of the average pfailure data (Fig. 2, bottom right) indicated a statistically significant benefit of cuing (valid vs. neutral), F(1, 18) = 5.05, p = .037, ηp2 = .22, as well as a significant effect of cost (invalid vs. neutral), F(1, 18) = 7.57, p = .013, ηp2 = .30, in memory-failure rate. Importantly, the magnitude of the cuing cost in pfailure interacted with the delay interval, F(1, 18) = 11.19, p = .004, ηp2 = .38, which was driven by the increased rate of memory failure between 2 and 4 s following the invalid cue, t(18) = 4.07, p < .001, Cohen’s d = 0.93. This suggests that when participants receive a cue indicating that a specific feature of an object is more relevant to the task, the less relevant feature is more likely to be lost from working memory, though loss does not take place immediately. In contrast, memory-failure rates for validly and neutrally cued features did not significantly change between 2 and 4 s, ts(18) < 0.45, ps > .250, which indicates quite stable maintenance of prioritized features.
We examined how working memory performance was affect by the retro-cue, relative to when a probe unexpectedly appeared at the usual time of the cue (i.e., on no-delay trials). Somewhat to our surprise, performance appeared worse in the no-delay baseline condition than on valid trials following a delay of 2 or 4 s, particularly for color working memory. Compared with no-delay trials, memory precision on cue trials was significantly better for validly cued colors at both 2 s, t(18) = 2.71, p = .014, Cohen’s d = 0.62, and 4 s, t(18) = 2.33, p = .031, Cohen’s d = 0.54, and memory failure was also reduced for validly cued colors at 2 s, t(18) = 2.06, p = 0.054, Cohen’s d = 0.47, and at 4 s, t(18) = 2.40, p = 0.027, Cohen’s d = 0.55. Improved performance following a retro-cue has sometimes been attributed to the existence of a fragile visual short-term memory (Sligte, Scholte, & Lamme, 2008) or to the protection of the cued items from potentially distracting effects that might occur with presentation of the test display (Makovski, Sussman, & Jiang, 2008; Souza, Rerko, & Oberauer, 2016). We hypothesized that the unexpected appearance of the probe display on infrequent no-delay trials likely had a disruptive effect on memory performance. To better evaluate the impact of retro-cues on the time course of memory representations, we controlled for this factor in Experiment 2.
In summary, we found that prioritizing a particular feature of an already encoded object led to enhanced working memory performance of that feature, both in terms of representational precision and probability of successful retention, which indicates that objects in working memory can be deconstructed into their component features. However, this prioritization benefit was associated with increased rates of memory failure for the deprioritized feature, which suggests some form of resource sharing among the multiple features of an object.
Experiment 2
How might retrospective cuing of a feature lead to superior memory performance, in some cases exceeding the performance observed in the no-delay control condition? One possibility is that retro-cues can somehow allow for the recovery of additional feature information over the delay period (cf. Souza et al., 2016). Alternatively, the retro-cue might simply protect the cued feature from deteriorating over time. According to this latter account, VWM performance was disproportionately impaired on no-delay trials in Experiment 1 because of their unexpected nature. To avoid such costs, we now presented no-delay trials in a separate block. We also excluded the invalid-cue condition to focus on the mechanisms underlying the benefits of reprioritization.
Method
Participants
Seventeen volunteers (3 male, 14 female; age: 19–28 years) with normal color vision and visual acuity completed the experiment for course credit or monetary compensation. One participant was excluded for having unusually large error magnitudes in feature reports (> 2.5 SD from the group mean), which resulted in a final data set of 16 participants. The sample size of 16 was deemed sufficient to detect the effects of cuing and delay duration, on the basis of the results of Experiment 1. The study was conducted according to procedures approved by the Vanderbilt University Institutional Review Board.
Apparatus and stimuli
The apparatus and stimuli were identical to those in Experiment 1, with the following minor modifications. The CIE L*a*b* coordinates of the stimuli were changed by centering the color ring at L* = 72, a* = 0, b* = 0, with a radius of 40, and by varying L* between 30.8 and 72 units. As a result, the color saturation was reduced from 50 to 40 units, and luminance contrast was reduced from 67% to 40%. These changes were intended to promote the encoding of metrically precise color information. Also, the radius of the color and gray wheels of the probe display was changed from 7.2° to 6°.
Procedure
The design was identical to that used in Experiment 1, except for the following changes. No-delay trials and retro-cue trials were presented in separate blocks, and only valid- and neutral-cue conditions were tested. Catch trials were no longer included because the feature cues were now 100% predictive of the to-be-probed feature. In Experiment 2, we also introduced an articulatory-suppression procedure to discourage verbal strategies that might be used to help remember the colors of the gratings.
At the beginning of each trial, three randomly chosen digits (colored white and subtending 2.2° × 0.9°) were presented at fixation for 1 s, and participants were asked to repeat them aloud until the end of the trial. After a 1-s fixation interval, the sample array for the VWM task appeared for 700 ms. The VWM component of the trial was the same as in Experiment 1, except that the retro-cue remained on the screen until the probe appeared with a 2- or 4-s SOA. After the feature report was complete, there was a 16.7% chance that participants would be prompted to report the three digits by typing them on the screen.
Each session consisted of 240 trials divided into 10 blocks of 24 trials each. Two blocks consisted of the no-delay condition, and the remaining eight blocks involved the retro-cue condition, in which valid- and neutral-cue trials were randomly intermixed. Each no-delay block was interleaved with four retro-cue blocks, with the position of the first no-delay block counterbalanced across sessions and participants. Each participant completed a total of 960 trials distributed across four 1-hr sessions. These included 96 trials for each combination of feature dimension (color and orientation), cue type (valid and neutral), and cue-to-probe SOA (2 and 4 s). The no-delay condition also had 96 trials for each feature dimension. We also obtained digit reports from each participant on 160 trials.
Results
Mean accuracy on the digit task was 95.1% (SD = 4.7%). The nearly perfect performance in this task indicates that participants rehearsed the digits reliably over the period of the retention interval. Response-error histograms and best-fitting mixture distributions for Experiment 2 are presented in Figures S3 and S4 in the Supplemental Material.
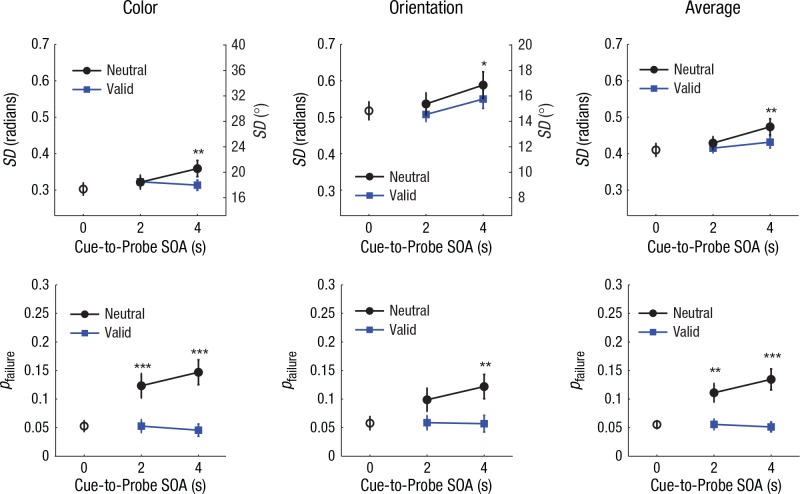
The results of Experiment 2 revealed significantly better memory precision and retention rates on valid trials than on neutral trials. Estimates of SD were significantly lower for features that could be reprioritized on the basis of a valid cue (Fig. 3, top row), F(1, 15) = 11.95, p = .004, ηp2 = .44. Validly cued features were also less likely to be lost from memory (Fig. 3, bottom row), as shown by a significant main effect of cue type on pfailure, F(1, 15) = 43.91, p < .001, ηp2 = .75. While the cuing benefit in pfailure tended to be greater in magnitude for color than for orientation, as indicated by a significant interaction effect between cue type and feature on pfailure, F(1, 15) = 4.68, p = .047, ηp2 = .24, this cuing effect was pronounced for both features, with memory-failure rates for neutrally cued features more than twice as high as those for validly cued features.
Fig. 3.
Mixture-model estimates of standard deviation (SD; top row) and probability of memory failure (pfailure; bottom row) in Experiment 2 (n = 16), separately for color, orientation, and average performance across both features. Results for each model are shown as a function of cue-to-probe stimulus onset asynchrony (SOA) and cue type. For both SD and pfailure, higher values on the left y-axes represent poorer working memory performance. The SD values for color and orientation were plotted on the same scale after conversion to a common circular space (0–2π radians); the corresponding degree values for each feature are shown on the right y-axes. The open circles plotted at 0-s SOA show the results from no-delay trials, when there was no retrospective cue (retro-cue). The color-coded asterisks denote significant differences between the no-delay baseline condition and individual retro-cue conditions (*p < .05, **p < .01, ***p < .001, based on two-tailed paired-samples t tests). Error bars represent ±1 SEM.
We observed a significant overall decline in memory precision between 2 and 4 s following the cue, F(1, 15) = 5.92, p = .028, ηp2 = .28, but this effect of SOA on SD did not significantly interact with cue type, F(1, 15) = 1.66, p = .217, ηp2 = .10. However, planned comparisons across SOAs applied separately to each cue type revealed a statistically significant loss of memory precision for neutrally cued features, t(15) = 2.14, p = .049, Cohen’s d = 0.54, and a nonsignificant effect for validly cued features, t(15) = 1.51, p = .151, Cohen’s d = 0.38, which suggests that the rate of precision loss during this interval may be relatively attenuated for validly cued features. With respect to pfailure, we found no significant change between 2 and 4 s following either type of cue, as indicated by the lack of a main effect of SOA, F(1, 15) = 1.29, p > .250, ηp2 = .08, and the lack of an interaction effect between SOA and cue type, F(1, 15) = 2.25, p = .154, ηp2 = .13.
As can be seen in Figure 3, memory performance for validly cued features appeared very comparable with performance on no-delay trials, while performance became considerably worse when tested 2 or 4 s following a neutral cue. Planned comparisons with the no-delay condition revealed that memory precision was significantly worse for both color and orientation following a neutral cue after a 4-s delay—color: t(15) = 3.01, p = .009, Cohen’s d = 0.75; orientation: t(15) = 2.37, p = .032, Cohen’s d = 0.59. In contrast, we did not find any significant changes in memory precision for validly cued features with respect to the no-delay baseline, ts(15) < 1.59, ps > .133. These results are generally consistent with the hypothesis that prioritization of a feature in VWM may confer some protection from precision loss over time.
Memory-failure rates were also significantly elevated relative to the no-delay condition following the neutral cue, as early as 2 s for color, t(15) = 4.14, p < .001, Cohen’s d = 1.03, and 4 s for orientation, t(15) = 3.00, p = .009, Cohen’s d = 0.75. By contrast, pfailure for validly cued features did not significantly differ from pfailure rates in the no-delay condition at either delay interval, ts(15) < 0.72, ps > .488.
Thus, when participants had to maintain both the color and orientation of an object with equal priority, we observed a gradual deterioration of precision for the maintained features over delays of 2 and 4 s, as well as an overall increase in the likelihood of memory failure relative to the no-delay condition. In comparison, prioritization of a single feature led to better overall memory performance at these delay periods, which resulted in memory precision and retention rates indistinguishable from those in the no-delay condition. Importantly, we did not find any evidence of recovery of feature information following the retro-cue when appropriate measures were taken to avoid the potentially disruptive effects of presenting an unexpected test display.
Although these results are broadly consistent with the notion that valid retro-cues can attenuate the rate of information loss over time, a limitation of our findings was that the interaction effect between delay duration and cue type did not reach statistical significance. We hypothesized that Experiments 1 and 2 may have lacked sufficient power to detect the interaction effect, because of a combination of the small magnitude of the effect itself and variance resulting from the parameter-estimation process (see the Supplemental Material). In Experiment 3, we sought to provide conclusive evidence regarding the interaction between delay and cue type by addressing this issue of statistical power.
Experiment 3
In Experiment 3, we used cue-to-probe SOAs of 1 and 5 s (see Fig. 1c) because we reasoned that increasing the difference between delay durations should magnify any temporal interactions with retrospective cuing. To improve the reliability of parameter estimation, we increased the number of trials per condition from 96 to 150. In addition, we sought to rule out the possibility that participants might rely on an unnatural strategy of encoding the color and orientation of each stimulus as two separate unbound features. To limit such strategies, we presented the sample array for only 150 ms, comparable with the duration used in many VWM studies.
Method
Participants
Twenty-four volunteers (9 male, 15 female; age: 19–33 years) with normal color vision and visual acuity completed this five-session experiment for course credit or monetary compensation. Two participants were replaced after completing only two or three sessions because they did not meet the criterion that average accuracy should be at least 75% for both features (see the Procedure from Experiment 1).
Sample size was determined on the basis of a power analysis, using the data from Experiment 2 and simulations to examine the effect of number of trials on the stability of parameter estimates (see the Supplemental Material). The test for the interaction effect in a 2 × 2 repeated measures design was conceptualized as a one-sample t test against zero for the mean interaction score (X11 – X12 – X21 + X22). Effect sizes (Cohen’s ds) for the original SD and pfailure data were 0.32 and 0.38, respectively. By extrapolating the data points linearly over time and accounting for reduced estimation noise by increasing the number of trials per condition, we predicted the effect size for the new experimental design to be 0.63 for SD and 0.74 for pfailure. With a two-tailed alpha of .05, the required sample sizes for 80%, 85%, and 90% power were 22, 25, and 29 for SD and 17, 19, and 22 for pfailure. We decided that a sample size of 24 would provide adequate power to detect the interaction effects in both parameters.
Apparatus, stimuli, and procedure
The apparatus, stimuli, and procedure were identical to those in Experiment 2, with the following exceptions. For the articulatory-suppression task, three random digits were presented just above the fixation point for 1 s, followed by a 1-s fixation period. The timing of the subsequent events is depicted in Figure 1c. The sample array was presented for 150 ms, followed by the patterned mask and the retro-cue (“C,” “O,” or “E”). The probe display appeared with a cue-to-probe SOA of 1 or 5 s. After completing the feature report, participants were asked to report the digits on randomly selected trials (16.7%). The no-delay baseline condition was omitted from Experiment 3.
Each participant completed five 1-hr sessions, each consisting of 240 trials divided into 10 blocks. Each participant completed a total of 1,200 cue trials, which resulted in 150 trials for each combination of probed feature (color and orientation), cue type (valid and neutral), and cue-to-probe SOA (1 and 5 s), as well as 200 trials of digit reports.
Results
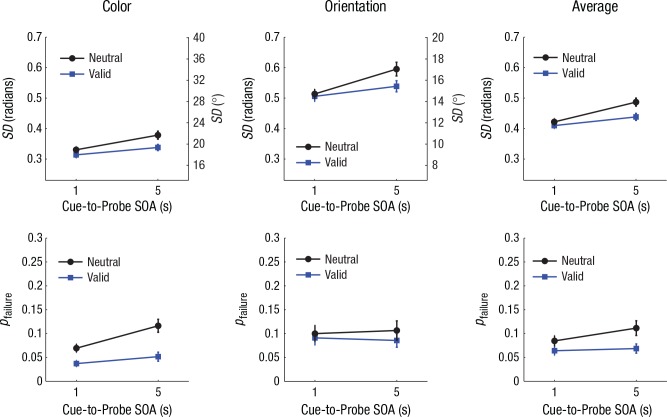
Mean accuracy on the verbal task was 98.2% (SD = 1.6%), which indicates reliable verbal rehearsal and reporting of the digits. Response-error histograms and best-fitting mixture distributions for Experiment 3 are presented in Figures S5 and S6 in the Supplemental Material. As shown in Figure 4, the mixture-modeling results revealed a robust benefit of valid retro-cues on memory precision, F(1, 23) = 36.53, p < .001, ηp2 = .61, and retention rate, F(1, 23) = 31.07, p < .001, ηp2 = .57. Also, we observed significant declines in memory precision and retention rate between trials with 1-s and 5-s delays—SD: F(1, 23) = 31.35, p < .001, ηp2 = .58; pfailure: F(1, 23) = 5.27, p = .031, ηp2 = .19. Critically, information loss during this interval was significantly reduced for valid trials compared with neutral trials, as demonstrated by significant interactions between SOA and cue type for estimates of memory—SD: F(1, 23) = 7.79, p = .010, ηp2 = .25; pfailure: F(1, 23) = 5.35, p = .030, ηp2 = .19. These interaction effects did not significantly differ between color and orientation, Fs(1, 23) < 0.84, ps > .250. Separate analyses of delay effects for each cue type indicated that memories for neutrally cued features underwent both the precision loss, t(23) = 5.59, p < .001, Cohen’s d = 1.14, and increased likelihood of complete termination, t(23) = 2.59, p = .016, Cohen’s d = 0.53, between 1 and 5 s following the cue. While memories for validly cued features became significantly less precise during this interval, t(23) = 3.01, p = .006, Cohen’s d = 0.61, there was no detectable increase in complete forgetting for these features, t(23) = 0.79, p > .250.
Fig. 4.
Mixture-model estimates of standard deviation (SD; top row) and probability of memory failure (pfailure; bottom row) in Experiment 3 (n = 24), separately for color, orientation, and average performance across both features. Results for each model are shown as a function of cue-to-probe stimulus onset asynchrony (SOA) and cue type. For both SD and pfailure, higher values on the left y-axes represent poorer working memory performance. The SD values for color and orientation were plotted on the same scale after conversion to a common circular space (0–2π radians); the corresponding degree values for each feature are shown on the right y-axes. Error bars represent ±1 SEM.
In summary, by using a wider range of delay durations, we found robust statistical evidence that retrospective cuing of a single feature dimension attenuates the loss of information from working memory over time. The cuing effects from the previous experiments were replicated, even with the brief presentation of the sample displays. These results strengthen the notion that features of an object may appear integrated during perception, but they are not obligatorily maintained as a bound unit in working memory.
Discussion
We found that multifeature objects in VWM underwent precision deterioration as well as complete termination within a few seconds after initial encoding. When participants had the opportunity to prioritize a specific feature of a stored object during the delay period, information loss was effectively minimized for that feature, which led to benefits in terms of both memory precision and retention rate. These benefits, however, were accompanied by an accelerated loss of information regarding the deprioritized feature. Thus, the rate of information loss from VWM was flexibly modulated by which feature of an object was prioritized during maintenance.
We propose that an active maintenance process, in the form of attention-based refreshing of memory traces (Awh & Jonides, 2001; Barrouillet & Camos, 2012), supports information persistence in VWM and that this process must be shared among multiple task-relevant features of an object. By focusing this maintenance process on a particular feature of a stored object, information about that feature can be more effectively protected against deterioration and forgetting over time. Information could be lost from VWM through various means, including random drifts of memory state resulting from intrinsic neural noise (Burak & Fiete, 2012; Compte, Brunel, Goldman-Rakic, & Wang, 2000), temporal decay (Barrouillet & Camos, 2012; Ricker, Spiegel, & Cowan, 2014), and interference among memory traces (Lewandowsky, Oberauer, & Brown, 2009; Souza & Oberauer, 2015). These potential sources of loss are not necessarily mutually exclusive. Whatever the precise sources of information loss might be, our results show that information held in VWM becomes more resistant to such influences when it is selectively prioritized by the top-down goals of the participant.
The processes underlying active maintenance of information over time can be conceptually distinguished from those that mediate the initial encoding of information into VWM. VWM encoding is limited by its storage capacity, which is typically construed as a fixed number of discrete memory slots or a continuous pool of resources (Luck & Vogel, 2013; Ma, Husain, & Bays, 2014; Pratte, Park, Rademaker, & Tong, 2017). While storage capacity is thought to determine the maximum amount of information that can be simultaneously held in VWM, active maintenance processes can influence the temporal stability of that information. At the encoding stage, the allocation of greater resources to a particular feature of an object can increase the amount of information obtained about that feature (Cowan et al., 2013; Fougnie et al., 2010; Oberauer & Eichenberger, 2013). However, reallocating resources to specific features of an already encoded object, or preferentially refreshing the memory trace of one feature over the other, can only modulate the rate at which the previously encoded information is lost over time.
Our findings demonstrate that multiple features of an object are not obligatorily maintained as a unitary representation in VWM. Instead, stored object representations can be unbound so that the active maintenance process can be focused on a particular task-relevant feature. While it is well-established that attention can enhance perceptual processing and subsequent encoding into VWM by prioritizing a particular feature of an object being viewed (e.g., Jehee, Brady, & Tong, 2011; Serences, Ester, Vogel, & Awh, 2009; Woodman & Vogel, 2008), our findings imply that feature-based attention can also operate on an object stored in VWM. When participants focused attention on a particular feature of the stored object, the attended feature remained more stable in VWM while the unattended feature was more likely to be forgotten over time. This is in line with previous work (Ko & Seiffert, 2009) showing that participants can selectively update one feature of an object in VWM without having to refresh its other features. Feature-selective memory failure has been reported previously under circumstances in which a large number of multifeature objects had to be encoded into VWM (Fougnie & Alvarez, 2011; see also Bays, Wu, & Husain, 2011). Here, we provide novel evidence that feature information can be lost over time even after each object in the sample array is fully attended and consolidated into VWM.
Our results challenge the assumption that visual objects are obligatorily represented as single integrated units in VWM and that the maintenance of multiple object features accrues no added cost. Instead, individual features of an object remain separable even after that object is fully encoded into VWM. The limited-processing resource for active maintenance must be shared among multiple task-relevant features of an object, leading to an accelerated loss of information about each individual feature over time.
Our findings have broad implications for the fields of working memory and attention research. Contrary to the commonly held view that information held in working memory remains stable over time, our results show that such information gradually becomes less precise and may be completely forgotten within a few seconds. Moreover, information is lost at a faster rate when one tries to remember more pieces of information, even when those bits represent the parts of a multifeature object. While working memory maintenance is imperfect, one can flexibly refocus attention in response to changing task demands, such that the most relevant information can be maintained in a more stable manner over time.
Supplementary Material
Footnotes
Action Editor: Edward S. Awh served as action editor for this article.
Declaration of Conflicting Interests: The authors declared that they had no conflicts of interest with respect to their authorship or the publication of this article.
Funding: This work was supported by National Science Foundation Grant BCS-1228526 to F. Tong and by National Institutes of Health (NIH) Institutional Research Training Grant 5T32EY007135-18 to J. L. Sy via the Vanderbilt Vision Research Center (VVRC). This research was facilitated by NIH Grant P30-EY-008126 to the VVRC.
Supplemental Material: Additional supporting information can be found at http://journals.sagepub.com/doi/suppl/10.1177/0956797617719949
Open Practices:

All data have been made publicly available via the Open Science Framework and can be accessed at https://osf.io/nfh28/. The complete Open Practices Disclosure for this article can be found at http://journals.sagepub.com/doi/suppl/10.1177/0956797617719949. This article has received the badge for Open Data. More information about the Open Practices badges can be found at http://www.psychologicalscience.org/publications/badges.
References
- Awh E., Jonides J. (2001). Overlapping mechanisms of attention and spatial working memory. Trends in Cognitive Sciences, 5, 119–126. doi: 10.1016/S1364-6613(00)01593-X [DOI] [PubMed] [Google Scholar]
- Barrouillet P., Camos V. (2012). As time goes by: Temporal constraints in working memory. Current Directions in Psychological Science, 21, 413–419. doi: 10.1177/0963721412459513 [DOI] [Google Scholar]
- Bays P. M., Wu E. Y., Husain M. (2011). Storage and binding of object features in visual working memory. Neuropsychologia, 49, 1622–1631. doi: 10.1016/j.neuropsychologia.2010.12.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blaser E., Pylyshyn Z. W., Holcombe A. O. (2000). Tracking an object through feature space. Nature, 408, 196–199. [DOI] [PubMed] [Google Scholar]
- Brainard D. H. (1997). The Psychophysics Toolbox. Spatial Vision, 10, 433–436. [PubMed] [Google Scholar]
- Burak Y., Fiete I. R. (2012). Fundamental limits on persistent activity in networks of noisy neurons. Proceedings of the National Academy of Sciences, USA, 109, 17645–17650. doi: 10.1073/pnas.1117386109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Compte A., Brunel N., Goldman-Rakic P. S., Wang X.-J. (2000). Synaptic mechanisms and network dynamics underlying spatial working memory in a cortical network model. Cerebral Cortex, 10, 910–923. doi: 10.1093/cercor/10.9.910 [DOI] [PubMed] [Google Scholar]
- Cowan N., Blume C. L., Saults J. S. (2013). Attention to attributes and objects in working memory. Journal of Experimental Psychology: Learning, Memory, and Cognition, 39, 731–747. doi: 10.1037/a0029687 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delvenne J.-F., Bruyer R. (2004). Does visual short-term memory store bound features? Visual Cognition, 11, 1–27. doi: 10.1080/13506280344000167 [DOI] [Google Scholar]
- Duncan J. (1984). Selective attention and the organization of visual information. Journal of Experimental Psychology: General, 113, 501–517. [DOI] [PubMed] [Google Scholar]
- Fougnie D., Alvarez G. A. (2011). Object features fail independently in visual working memory: Evidence for a probabilistic feature-store model. Journal of Vision, 11(12), Article 3. doi: 10.1167/11.12.3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fougnie D., Asplund C. L., Marois R. (2010). What are the units of storage in visual working memory? Journal of Vision, 10(12), Article 27. doi: 10.1167/10.12.27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irwin D. E., Andrews R. V. (1996). Integration and accumulation of information across saccadic eye movements. In Toshio I., McClelland J. L. (Eds.), Attention and Performance XVI: Information integration in perception and communication (pp. 125–155). Cambridge, MA: MIT Press. [Google Scholar]
- Jehee J. F. M., Brady D. K., Tong F. (2011). Attention improves encoding of task-relevant features in the human visual cortex. The Journal of Neuroscience, 31, 8210–8219. doi: 10.1523/JNEUROSCI.6153-09.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ko P. C., Seiffert A. E. (2009). Updating objects in visual short-term memory is feature selective. Memory & Cognition, 37, 909–923. doi: 10.3758/MC.37.6.909 [DOI] [PubMed] [Google Scholar]
- Lewandowsky S., Oberauer K., Brown G. D. A. (2009). No temporal decay in verbal short-term memory. Trends in Cognitive Sciences, 13, 120–126. doi: 10.1016/j.tics.2008.12.003 [DOI] [PubMed] [Google Scholar]
- Luck S. J., Vogel E. K. (1997). The capacity of visual working memory for features and conjunctions. Nature, 390, 279–281. doi: 10.1038/36846 [DOI] [PubMed] [Google Scholar]
- Luck S. J., Vogel E. K. (2013). Visual working memory capacity: From psychophysics and neurobiology to individual differences. Trends in Cognitive Sciences, 17, 391–400. doi: 10.1016/j.tics.2013.06.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma W. J., Husain M., Bays P. M. (2014). Changing concepts of working memory. Nature Neuroscience, 17, 347–356. doi: 10.1038/nn.3655 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makovski T., Sussman R., Jiang Y. V. (2008). Orienting attention in visual working memory reduces interference from memory probes. Journal of Experimental Psychology: Learning, Memory, and Cognition, 34, 369–380. doi: 10.1037/0278-7393.34.2.369 [DOI] [PubMed] [Google Scholar]
- Oberauer K., Eichenberger S. (2013). Visual working memory declines when more features must be remembered for each object. Memory & Cognition, 41, 1212–1227. doi: 10.3758/s13421-013-0333-6 [DOI] [PubMed] [Google Scholar]
- O’Craven K. M., Downing P. E., Kanwisher N. (1999). fMRI evidence for objects as the units of attentional selection. Nature, 401, 584–587. doi: 10.1038/44134 [DOI] [PubMed] [Google Scholar]
- Olson I. R., Jiang Y. (2002). Is visual short-term memory object based? Rejection of the “strong-object” hypothesis. Perception & Psychophysics, 64, 1055–1067. doi: 10.3758/BF03194756 [DOI] [PubMed] [Google Scholar]
- Pertzov Y., Bays P. M., Joseph S., Husain M. (2013). Rapid forgetting prevented by retrospective attention cues. Journal of Experimental Psychology: Human Perception and Performance, 39, 1224–1231. doi: 10.1037/a0030947 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips W. A. (1974). On the distinction between sensory storage and short-term visual memory. Perception & Psychophysics, 16, 283–290. doi: 10.3758/BF03203943 [DOI] [Google Scholar]
- Pratte M. S., Park Y. E., Rademaker R. L., Tong F. (2017). Accounting for stimulus-specific variation in precision reveals a discrete capacity limit in visual working memory. Journal of Experimental Psychology: Human Perception and Performance, 43, 6–17. doi: 10.1037/xhp0000302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ricker T. J., Spiegel L. R., Cowan N. (2014). Time-based loss in visual short-term memory is from trace decay, not temporal distinctiveness. Journal of Experimental Psychology: Learning, Memory, and Cognition, 40, 1510–1523. doi: 10.1037/xlm0000018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serences J. T., Ester E. F., Vogel E. K., Awh E. (2009). Stimulus-specific delay activity in human primary visual cortex. Psychological Science, 20, 207–214. doi: 10.1111/j.1467-9280.2009.02276.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sligte I. G., Scholte H. S., Lamme V. A. F. (2008). Are there multiple visual short-term memory stores? PLoS ONE, 3(2), Article e1699. doi: 10.1371/journal.pone.0001699 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Souza A. S., Oberauer K. (2015). Time-based forgetting in visual working memory reflects temporal distinctiveness, not decay. Psychonomic Bulletin & Review, 22, 156–162. doi: 10.3758/s13423-014-0652-z [DOI] [PubMed] [Google Scholar]
- Souza A. S., Oberauer K. (2016). In search of the focus of attention in working memory: 13 years of the retro-cue effect. Attention, Perception, & Psychophysics, 78, 1839–1860. doi: 10.3758/s13414-016-1108-5 [DOI] [PubMed] [Google Scholar]
- Souza A. S., Rerko L., Oberauer K. (2016). Getting more from visual working memory: Retro-cues enhance retrieval and protect from visual interference. Journal of Experimental Psychology: Human Perception and Performance, 42, 890–910. doi: 10.1037/xhp0000192 [DOI] [PubMed] [Google Scholar]
- Treisman A. (1996). The binding problem. Current Opinion in Neurobiology, 6, 171–178. doi: 10.1016/S0959-4388(96)80070-5 [DOI] [PubMed] [Google Scholar]
- Wheeler M. E., Treisman A. M. (2002). Binding in short-term visual memory. Journal of Experimental Psychology: General, 131, 48–64. doi: 10.1037/0096-3445.131.1.48 [DOI] [PubMed] [Google Scholar]
- Wilken P., Ma W. J. (2004). A detection theory account of change detection. Journal of Vision, 4(12), Article 11. doi: 10.1167/4.12.11 [DOI] [PubMed] [Google Scholar]
- Williams M., Hong S. W., Kang M.-S., Carlisle N. B., Woodman G. F. (2013). The benefit of forgetting. Psychonomic Bulletin & Review, 20, 348–355. doi: 10.3758/s13423-012-0354-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodman G. F., Vogel E. K. (2008). Selective storage and maintenance of an object’s features in visual working memory. Psychonomic Bulletin & Review, 15, 223–229. [DOI] [PubMed] [Google Scholar]
- Xu Y. (2002). Encoding color and shape from different parts of an object in visual short-term memory. Perception & Psychophysics, 64, 1260–1280. doi: 10.3758/BF03194770 [DOI] [PubMed] [Google Scholar]
- Zhang W., Luck S. J. (2008). Discrete fixed-resolution representations in visual working memory. Nature, 453, 233–235. doi: 10.1038/nature06860 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W., Luck S. J. (2009). Sudden death and gradual decay in visual working memory. Psychological Science, 20, 423–428. doi: 10.1111/j.1467-9280.2009.02322.x [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.