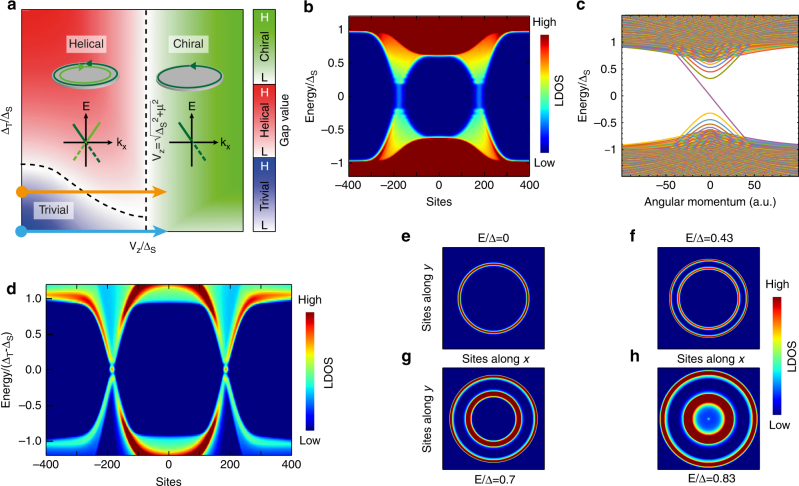
Fig. 3.

Theoretical calculations. a Phase diagram of 2D topological superconductivity as a function of the Zeeman field V _z and the triplet order parameter amplitude Δ_T. The black dashed lines show the transitions between the trivial and helical phases, as well as the transition between the helical and chiral phases. The insets show the typical behavior of the edge states for the helical case (with two counter-propagating edge states) and the chiral case (only one edge state whose chirality is determined by the orientation of the magnetic field). The color code corresponds to the values of the gap in each phase with one color for each phase. b Real space tight binding calculation of ρ(r, E) showing a Majorana edge state dispersing throughout the gap (parameters used for the calculation: t = 100, μ = 50, α = 200 and Δ_S = 140). No triplet pairing was used: Δ_T = 0. The diameter of the system is D = 500 sites. The Zeeman potential is given by V _z(r) = 120(1 − tanh(r − R _c)/w), with R _c = D/2 and w = 0.14D. c Energy dispersion as function of the angular momentum E(k _θ) with the same parameters used for the tight binding calculation in b showing a Majorana branch closing the gap. d Real space tight binding calculation of ρ(r, E) in the presence of a triplet pairing (Parameters used for the calculation: t = 100, μ = 50, Δ_S = 150, Δ_T = 60 and α = 0). The Zeeman potential is the same as in b. Note that in all our numerical calculations, the X-shape features originate from a real space partial gap closing. This can be traced back to the smoothness of the Zeeman field decaying over a scale $w\gg k_F^{-1}$. In the more realistic limit, $w\ll R_c<\xi$, we expect that only the edges states will cross the gap and give rise to these X-shape features. e–h Calculated LDOS with the same parameters than in d for 4 different energies: E/Δ = 0, 0.43, 0.7, and 0.83