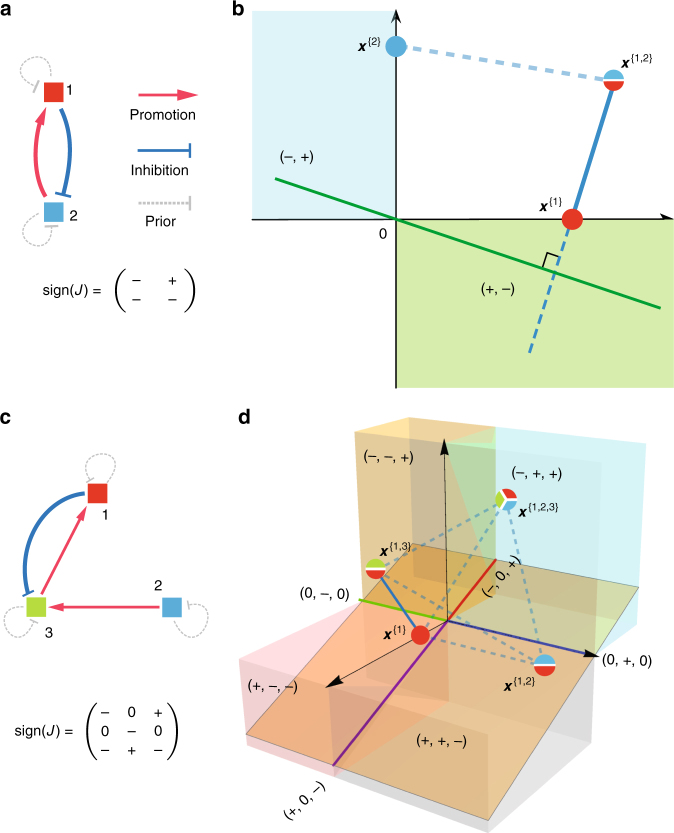
Fig. 1.

Inferring ecological interaction types for a small microbial community. The interaction types are coded as the sign-pattern of the Jacobian matrix. a For a microbial community of two taxa, its ecological network and the sign-pattern of the corresponding Jacobian matrix are shown here. b There are three possible steady-state samples (shown as colored pie charts), and two of them ${\mathit{x}}^{\left\{1,2\right\}},{\mathit{x}}^{\left\{1\right\}}$ share taxon 1. We calculate the green line that passes through the origin and is perpendicular to the vector $\left({\mathit{x}}^{\left\{1,2\right\}}-{\mathit{x}}^{\left\{1\right\}}\right)$ (shown as a blue line segment). This green line crosses the origin, and two other orthants (shown in light cyan and green), offering a set of possible sign-patterns: $\left(0,0\right),\left(-,-\right)$ and $\left(+,-\right)$, for which ${\mathit{s}}_1=\left(\mathrm{sign}\left(J_{11}\right),\mathrm{sign}\left(J_{12}\right)\right)$ may belong to. Provided that $J_{11}<0$, we conclude that ${\mathit{s}}_1=\left(-,+\right)$. c For a microbial community of three taxa, its ecological network and the sign-pattern of the corresponding Jacobian matrix are shown here. d There are seven possible steady-state samples, and we plot four of them that share taxon 1. Consider a line segment $\left({\mathit{x}}^{\left\{1,3\right\}}-{\mathit{x}}^{\left\{1\right\}}\right)$ (solid blue). We calculate the orange plane that passes through the origin and is perpendicular to this solid blue line. This orange plane crosses nine regions: the origin and the other eight regions (denoted in different color cubes, color lines), offering nine possible sign-patterns for s ₁. We can consider another line segment that connects two steady-state samples sharing taxon 1, say, ${\mathit{x}}^{\left\{1,3\right\}}$ and ${\mathit{x}}^{\left\{1,2,3\right\}}$, and repeat the above procedure. We do this for all the sample pairs (dashed blue lines), record the regions crossed by the corresponding orthogonal planes. Finally, the intersection of the regions crossed by all those orthogonal hyperplanes yields a minimum set of sign-patterns ${\widehat{\mathcal{S}}}_1=\left\{\left(-,0,+\right),\left(0,0,0\right),\left(+,0,-\right)\right\}$ that s ₁ may belong to. If we know that $J_{11}<0$, then we can uniquely determine ${\mathit{s}}_1=\left(-,0,+\right)$