FtsZ Constriction Force – Curved Protofilaments Bending Membranes

Abstract

FtsZ assembles in vitro into protofilaments (pfs) that are one subunit thick and ~50 subunits long. In vivo these pfs assemble further into the Z ring, which, along with accessory division proteins, constricts to divide the cell. We have reconstituted Z rings in liposomes in vitro, using pure FtsZ that was modified with a membrane targeting sequence to directly bind the membrane. This FtsZ-mts assembled Z rings and constricted the liposomes without any accessory proteins. We proposed that the force for constriction was generated by a conformational change from straight to curved pfs. Evidence supporting this mechanism came from switching the membrane tether to the opposite side of the pf. These switched-tether pfs assembled “inside-out” Z rings, and squeezed the liposomes from the outside, as expected for the bending model. We propose three steps for the full process of cytokinesis: (a) pf bending generates a constriction force on the inner membrane, but the rigid peptidoglycan wall initially prevents any invagination; (b) downstream proteins associate to the Z ring and remodel the peptidoglycan, permitting it to follow the constricting FtsZ to a diameter of ~250 nm; the final steps of closure of the septum and membrane fusion are achieved by excess membrane synthesis and membrane fluctuations.

Introduction

In 2010 we published an extensive review of FtsZ, covering in vitro assembly studies as well as mechanisms in vivo (Erickson et al. 2010). In the present article we focus on studies that have provided new insights, along with some repetition of issues that are still debated. The major question is, what generates the constriction force for bacterial cytokinesis? We will review the evidence that the force is generated primarily by FtsZ, specifically by the conformational change of FtsZ protofilaments (pfs) from straight to curved, generating a bending force on the membrane.

Straight pfs and Minirings

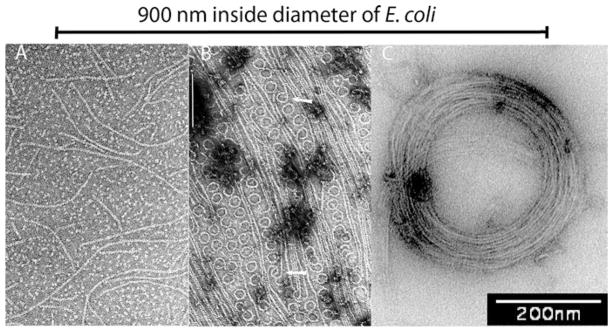
When Escherichia coli FtsZ (EcFtsZ) is assembled to steady state with GTP, negative stain EM shows pfs that are one subunit wide and 100–200 nm (25–50 subunits) long (Fig. 5.1a). Erickson et al. (1996) found that when FtsZ was assembled onto cationic lipid monolayers, many pfs were straight, and others were highly curved to form minirings, with an outside diameter of 24 nm (Fig. 5.1b). In some cases one could see an abrupt transition from the straight pf to the highly curved conformation (arrow, Fig. 5.1b). Tubulin shows a similar transition from straight pfs in the microtubule wall, to spirals and rings that are released upon disassembly of tubulin-GDP (McIntosh et al. 2010).

Fig. 5.1.

Three conformations of FtsZ pfs. (a) pfs assembled in GTP are mostly straight, although some have intermediate curvature. (b) pfs assembled in GDP and adsorbed to a cationic lipid monolayer show the highly curved miniring conformation, mixed with straight pfs (Reprinted from Erickson et al. 1996 with permission of the author). (c) Toroids assembled in 1.6% methyl cellulose, where pfs are in the intermediate curved conformation (micrograph provided by Max Housman; these are somewhat larger than the 200 nm diameter reported previously (Popp et al. 2009)). The diameter of an undivided bacterium is indicated on top

pf curvature similar to EcFtsZ minirings has been documented in only a few species. Caulobacter crescentus FtsZ assembles rings or spirals of 34–43 nm diameter in GDP and GTP-Mg, respectively, when stabilized by the accessory protein FzlA (Goley et al. 2010). Methanococcus jannaschii FtsZ assembled spiral ribbons about 30 nm in diameter in ficoll plus GDP (Huecas and Andreu 2004) or in mant-GTP (Huecas et al. 2015). A crystal form of Mycobacterium tuberculosis FtsZ showed antiparallel pfs in a tight spiral (Li et al. 2013). However, as discussed below, the curvature of these spirals is the opposite to that of EcFtsZ minirings.

The Intermediate Curved pf Conformation

In addition to the straight and highly curved minirings, there is an “intermediate curved conformation,” with a diameter of ~100–300 nm. For EcFtsZ this is often seen as pf segments of uniform curvature, mixed with straight pfs (e.g., Fig. 1B, C in (Romberg et al. 2001); Fig. 3A, B in (Huecas et al. 2008); Fig. 4A–C in (Dajkovic et al. 2008). Under some conditions the pfs form closed circles, 160–250 nm in diameter that have been imaged by negative stain EM (Gonzalez et al. 2005; Chen et al. 2005). This curved conformation is highly favored when pfs are adsorbed to mica and imaged by AFM (Hamon et al. 2009; Mateos-Gil et al. 2012; Mingorance et al. 2005). The most reproducible production of intermediate curved pfs is assembly in polyvinyl alcohol or methyl cellulose, which are crowding reagents mimicking in the vivo condition (Popp et al. 2009). Here FtsZ assembles into a variety of toroids and helical pf bundles with diameters varying from 150 to 500 nm, depending on solution conditions. These are readily imaged by negative stain EM (Fig. 5.1c).

The intermediate curved conformation appears to be much more widespread than the miniring, and has been documented for FtsZ pfs from several species. Bacillus subtilis FtsZ (BsFtsZ) forms toroids that are 150–300 nm in diameter, mixed with straight pfs and bundles (Buske and Levin 2012; Michie et al. 2006). The curved pfs and toroids of BsFtsZ and Staphylococcus aureus FtsZ are enhanced by the drugs PC190723 and 8j, (Adams et al. 2011; Andreu et al. 2010). M. tuberculosis FtsZ assembled 200–250 nm toroids in methyl cellulose (Popp et al. 2010). C. crescentus FtsZ (CcFtsZ) assembled circles of ~75 nm diameter when stabilized by the protein FzlA in GMPCPP or in GTP plus EDTA (which blocks GTP hydrolysis) (Goley et al. 2010). Assembly of CcFtsZ alone in GTP gave uniformly curved pfs of this same curvature mixed with straight pfs (Goley et al. 2010; Milam and Erickson 2013). These probably correspond to the intermediate curved conformation. (As mentioned above, CcFtsZ also assembles circles of 34–43 nm diameter, which are probably the miniring conformation.) Co-assembly of EcFtsZ and FtsA* in vitro produced striking curved polymer bundles, often curling off the ends of straight bundles (Beuria et al. 2009). This is reminiscent of the toroids spooling off the ends of straight pf bundles in yeast (Srinivasan et al. 2008), mentioned below.

Some studies have imaged toroids by light microscopy. Srinivasan et al. (2008) expressed EcFtsZ-GFP in yeast and found a mixture of toroids and straight pf bundles. Many of the toroids were large enough (0.5 μm diameter) to resolve by conventional light microscopy, but there were also many smaller round patches that were probably toroids, but too small for light microscopy to resolve the hollow center. Similar mixtures of straight pf bundles and toroids were assembled by FtsZ from M. tuberculosis and Xanthomonas, attesting to the generality of the process. In one time series a yeast cell was initially filled with straight pf bundles, which later transitioned to toroids. Importantly, the toroids were often located on the end of a straight pf bundle, suggesting a transition where the straight pf bundle was spooled into the toroid (Srinivasan et al. 2008).

Toroids ~200 nm in diameter were imaged by light microscopy in Arabidopsis, under conditions where FtsZ2-GFP was overexpressed, or when Z-ring modulating factors ARC6 or MinE were deleted (Johnson et al. 2015). These toroids required super-resolution light microscopy for optimal resolution. Previous studies of chloroplast FtsZ had imaged small round patches under related conditions (Fujiwara et al. 2009; Zhang et al. 2013); these are likely toroids, but the conventional fluorescence microscopy used in these studies did not resolve the hollow center. In all of these studies the toroids were frequently attached to the end a linear filament, similar to the spooling of EcFtsZ seen in yeast (Srinivasan et al. 2008).

The preferred curvature of FtsZ was elegantly explored in an in vitro study where inside-out Z rings were assembled on lipid-coated capillaries of varying diameter (Arumugam et al. 2012). For capillary diameters of 500 nm or above, the Z rings were perpendicular to the axis, as expected if their preferred curvature was <500 nm. For capillary diameters 100–500 nm the Z rings were tilted. The tilt could be produced if the diameter of the capillary were smaller than the preferred curvature, or if the pfs had a helical pitch. Arumugam et al. obtained a good fit for a model with a native helix diameter of 55 nm and a pitch of 150 nm. A comparable fit could probably be obtained with a native diameter of 200 nm and a smaller pitch. Overall these measurements seem consistent with the intermediate curved pf, 100–300 nm in diameter, being the preferred conformation in the inside-out Z rings.

What Induces the Transition from Straight to Curved pfs?

The miniring conformation was discovered first (Erickson et al. 1996) and has received much emphasis. The simplest story of the mechanism was that GTP favored the straight conformation and GDP the miniring. This was supported by the observation of two forms of EcFtsZ polymers stabilized by DEAE dextran. In GMPCPP, or in GTP plus EDTA (which permits assembly but blocks GTP hydrolysis), the assembly formed sheets of straight pfs, while in GDP it formed helical tubes of the same diameter as minirings (Lu et al. 2000). However, this is an oversimplification. The mix of minirings and straight pfs shown in Fig. 5.1b was obtained in GDP. Polymers at steady state contain 20–50% GDP (Chen and Erickson 2009; Romberg and Mitchison 2004), but negative stain EM shows mostly straight pfs. The crystal structure of SaFtsZ shows it assembled into straight pfs, but the bound nucleotide is GDP (Matsui et al. 2012).

The intermediate curved conformation is observed more generally across species, and we think it is presently the best candidate for constriction-force generation. The intermediate curvature does not appear to be generated by GTP hydrolysis, since we have observed curved pfs of EcFtsZ in GMPCPP, and in pfs assembled by the mutant D212A, which is defective in hydrolysis (unpublished observations). The 75 nm circles of CcFtsZ were assembled in GMPCPP or in GTP plus EDTA, which blocks hydrolysis (Goley et al. 2011). Most important, Popp et al. (2010) reproducibly obtained toroids and spiral pf bundles in non-hydrolyzable GMPPNP and in GTP plus EDTA.

One thing that seems to favor the transition from straight to curved is contact with a surface. This is suggested by the strong preference for curved pfs when they are adsorbed to mica (Hamon et al. 2009; Mingorance et al. 2005). Tethering pfs to a phospholipid membrane, or contacts with neighboring filaments in pf bundles may similarly induce the transition. In contrast, single circles of intermediate curved pfs imaged by negative stain EM were presumably formed in solution by single pfs (Adams et al. 2011; Chen et al. 2005; Gonzalez et al. 2005). Overall, there is no consistent model explaining the transition from straight to curved pfs. The kinetics and thermodynamics of this important mechanism still need to be worked out.

Curved pfs Can Bend Membranes and Generate a Constriction Force

It was suggested in 1997 that FtsZ might generate the constriction force for cytokinesis by itself, without any motor protein, by using the conformational change from the straight to curved pf (Erickson 1997) (Fig. 5.2). For the next 10 years there was no way to test this hypothesis. In 2008 the reconstitution of Z rings in vitro provided the needed breakthrough (Osawa et al. 2008). This reconstitution was achieved by fusing an amphipathic helix (membrane targeting sequence, or mts) to the C terminus of FtsZ, so it could tether itself to the membrane. When this FtsZ-mts was incorporated inside tubular liposomes, it spontaneously assembled Z rings, and these Z rings constricted the liposome. Both Z-ring assembly and constriction were achieved with purified FtsZ-mts; no other protein was required. The constriction force generated by FtsZ was strong enough to invaginate multilamellar lipid vesicles that were up to 1 μm thick.

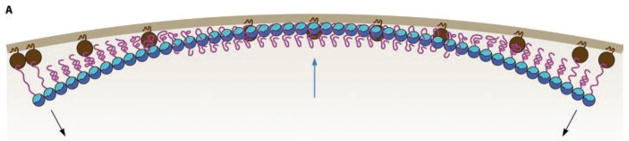
Fig. 5.2.

Model for constriction force generated by pf curvature bending the membrane. The brown arc represents the inner membrane of the undivided E. coli. The brown spheres are FtsA, which has an amphipathic helix that inserts into the membrane. The blue and cyan spheres are the globular domains of FtsZ. The magenta line is the C terminus of FtsZ, which comprises a flexible linker and a short peptide that binds to FtsA. FtsZ is shown here as a pf that is straining to adopt a curved conformation. It pulls the membrane inward from its ends, and pushes outward at its middle, generating a bending force (Reprinted from Erickson et al. 2010 with permission of the author)

The constriction observed in this reconstituted system was consistent with the curvature hypothesis but did not prove it. Evidence in favor of pf curvature as the mechanism of constriction force was obtained by applying FtsZ-mts to the outside of large, unilamellar liposomes. There it formed patches that bent the membrane into concave depressions (Osawa et al. 2009). This direction of the bending was the same as inside liposomes, where it binds to the concave inner surface and constricts it to be more concave. These concave depressions on the outside of large liposomes were also observed by Arumugam et al. (2012).

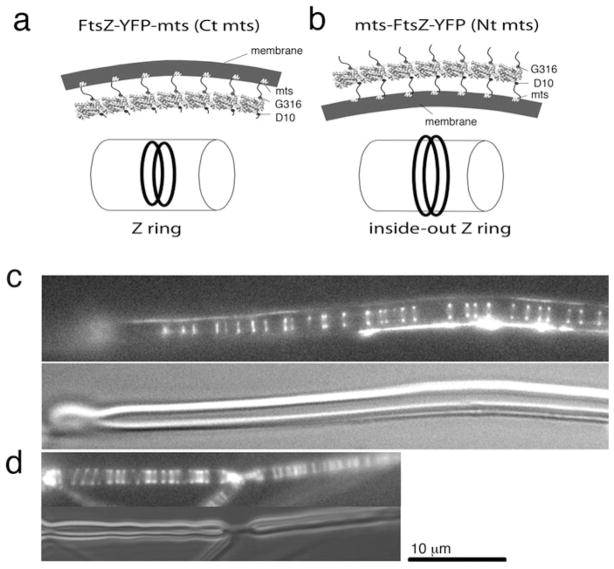
The most definitive evidence that pf curvature generates the constriction force was obtained by switching the membrane tether to the opposite side of the pf. This was possible for FtsZ, because the N and C termini are flexible peptides emerging from the globular domain about 180° apart. The normal C-terminal attachment in FtsZ-mts was predicted to be on the outside of the curved pf. Switching the attachment to the N terminus gave mts-FtsZ, which would place the mts on the inside of the curved pf (Fig. 5.3). As predicted by the bending hypothesis, mts-FtsZ assembled Z rings on the outside of tubular liposomes (Osawa and Erickson 2011). Remarkably, these “inside-out Z rings” also generated a constriction force, squeezing the liposomes from the outside. These experiments provided strong support for the pf curvature hypothesis.

Fig. 5.3.

(a) The normal tether on the C terminus is on the outside of the curved pf, and attaches to the concave membrane on the inside of a liposome or cell. (b) Switching the tether to the N terminus places it on the inside of the curved pf, for attachment to the convex surface on the outside of a liposome. (c) Z rings inside a tubular liposome reconstituted from FtsZ-mts. (d) Inside-out Z rings assembled on the outside of a liposome by mts-FtsZ. In (c) and (d) the upper panel shows FtsZ imaged by fluorescence, and the lower panels show the liposome imaged by DIC (Reprinted from Osawa et al. 2008; Osawa and Erickson 2011 with permission of the authors)

Tubulin pfs also have a curved conformation, which forms a bulge at the end of a disassembling MT as the pfs peel away. Curved tubulin pfs have been shown to generate force, since the bulge they create can drag an attached chromosome (McIntosh et al. 2010). There is, however, an apparent contradiction between the curvature of FtsZ and tubulin. It is well established for tubulin rings that the C terminus, corresponding to the outside of a MT, is on the inside of the ring (Moores and Milligan 2008; Nawrotek et al. 2011; Tan et al. 2008; Wang and Nogales 2005). In contrast, our model places the C terminus of FtsZ on the outside (Fig. 5.2). We have recently resolved this apparent contradiction by fusing a protein tag onto the C terminus of FtsZ and observing its location on tubes assembled in DEAE dextran and GDP. These tubes are analogs of FtsZ minirings (Lu et al. 2000). Thin section EM showed that the C-terminal appendage is on the outside of the tubes (Housman et al. 2016). Apparently, in the evolution of MTs the tubulin pfs switched to curve in the opposite direction to FtsZ.

Modeling studies have predicted that both FtsZ and tubulin pfs can bend in both directions (Grafmuller and Voth 2011; Hsin et al. 2012; Ramirez-Aportela et al. 2014; Theisen et al. 2012). A recent crystal structure of MtbFtsZ showed antiparallel pf pairs in a tight spiral, with the C terminus facing inward (Li et al. 2013). This curvature is the opposite of the EcFtsZ miniring/tube, and it is not yet clear if it is physiologically important. It has also not yet been determined what is the direction of the intermediate curved conformation. Since this form is likely the one generating the constriction force, we suggest that it has the C terminus on the outside facing the membrane, like the miniring.

FtsZ pfs Are Mechanically Rigid

If the curved pfs are to generate a meaningful bending force on the membrane, they must be mechanically rigid. It is still not universally recognized how rigid the FtsZ pfs really are. For example, a recent review commented “recent work has suggested that FtsZ filaments may be too flexible to bend membranes…” (Eun et al. 2015). Ramirez-Aportela et al. (2014) commented on “…the large disparity in measurements [of persistence length] found in the literature for GTP/GDP filaments of FtsZ from other species. For example, in a cryo-electron microscopy study of E. coli FtsZ (EcFtsZ), Turner et al. (2012) visualized relatively straight filaments with a persistence length of 1.4 μm. In contrast, we previously estimated protofilament persistence length values in the 100 nm range, also using cryo-electron microscopy of EcFtsZ but neglecting intrinsic filament curvature (Huecas et al. 2008).” Dajkovic et al. (2008) also reported measuring a very low persistence length: Lp ~180 nm.

“…neglecting intrinsic filament curvature” is the key issue here. As we have noted previously (Erickson et al. 2010), in the two studies reporting very low persistence length (Dajkovic et al. 2008; Huecas et al. 2008) the authors assumed that the relaxed pf was straight, and that any curvature was due to random thermal bending. However, one can see in their micrographs (Fig. 3 in (Huecas et al. 2008)) that a significant fraction of the pfs have a fairly uniform curvature corresponding to the ~200 nm diameter intermediate curved conformation. The intermediate curved conformation was not well recognized at that time, so it is understandable that these curved pfs might have been attributed to thermal bending. In a separate study Hörger et al. (2008) used AFM to image pfs adsorbed to mica. These mica-adsorbed pfs seem to transition completely to the intermediate curved conformation, and this was recognized by the authors as the natural conformation of these pfs. They concluded that the pfs had a preferred curvature of 200 nm diameter, and a variation corresponding to a persistence length of ~4 μm. This is somewhat larger than the 1.4 μm of Turner et al, possibly because their pfs were adsorbed to mica, leaving them only the plane of the mica for thermal fluctuations.

The study by Turner et al. (2012) used cryoEM of samples where the pfs were suspended in aqueous medium over holes in the carbon film. The pfs had no contact with a carbon film, and they were widely dispersed to avoid any pf-pf contact. Their pfs were all straight (it is not clear why none were in the intermediate curved conformation). The small curvatures they measured were attributed to thermal bending, giving a persistence length of 1.4 μm. This is very close to the 2.9 μm estimated by Mickey and Howard (1995) for a single pf extracted from a MT. This study by Turner et al. should now be considered the definitive measurement of the mechanical rigidity of the FtsZ pfs.

This mechanical rigidity is not specific for FtsZ, but is a general property of globular proteins and their polymers. Twenty years ago Howard and colleagues measured the flexural rigidity of MTs and actin filaments suspended in aqueous solution (Gittes et al. 1993). They concluded that “If tubulin were homogeneous and isotropic, then the microtubule’s Young’s modulus would be ~1.2 GPa, similar to Plexiglas and rigid plastics”. The generalization is that globular proteins and their polymers share this rigidity. Plexiglas is very rigid, and so are proteins.

In Vitro Systems Reconstituted with FtsZ and FtsA

In bacteria, FtsZ is tethered to the membrane by FtsA. FtsA has an amphipathic helix that binds the membrane, and FtsZ has a conserved C-terminal peptide that binds to the globular domain of FtsA (Pichoff and Lutkenhaus 2005) (Fig. 5.2). FtsA is an actin homolog, and it can assemble filaments when bound to a lipid bilayer (Szwedziak et al. 2012). Our original reconstitution in liposomes used FtsZ-mts, where the mts could tether FtsZ directly to the membrane, bypassing FtsA. More recently, three studies have achieved reconstitutions using the natural two-protein system, FtsZ plus FtsA, where the FtsZ pfs are tethered to the membrane by FtsA. Each study had to solve the problem that EcFtsA has been difficult to express and work with in vitro.

Osawa and Erickson (2013) reported a reconstitution using the E. coli mutant FtsA*, which is fully functional in vivo and gives much better results in vitro than wild type EcFtsA (Beuria et al. 2009; Geissler et al. 2007). When a 1:1 mixture of FtsZ-YFP:FtsA was incorporated inside large unilamellar vesicles, a small fraction of the liposomes developed fluorescent Z rings that constricted the liposome to the point of membrane contact (Fig. 5.4). Then the membranes abruptly formed a flat septum, apparently having fused at the point of tightest constriction. FtsA was essential to obtain constriction and septation of these large liposomes. Without FtsA, FtsZ-mts bound to and bent the membrane to form protrusions, and typically assumed the shape of small Z rings ~1 μm in diameter. Rarely a larger Z ring formed, but instead of constricting the liposome, the Z ring appeared to slide down the side as it constricted. Thus FtsA seems necessary to promote a stable Z ring around the center of the vesicle, but the mechanism is not yet known.

Fig. 5.4.

Z rings reconstituted from EcFtsZ-YFP plus FtsA in a large unilamellar vesicle. Numbers on the lower left give time in s. At 66 s the vesicle is largely constricted, by a prominent Z ring seen by fluorescence at 96 s. At 603 s the constriction has advanced to where the invaginating membrane shows two dots about 1 μm apart. At 777 s the membranes appear to have fused into a broad, flat septum between the two vesicles, and the FtsZ-YFP is a diffuse smear at one end (800 s) (Adapted from Osawa and Erickson 2013 with permission of the authors)

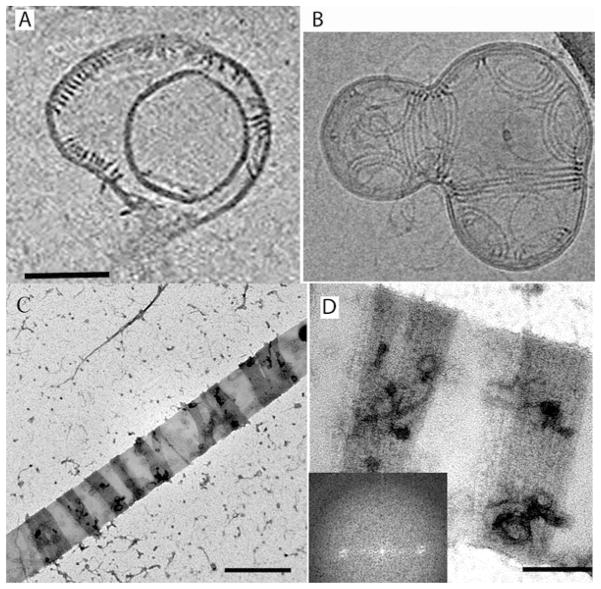
Szwedziak et al. (2014) recently presented beautiful cryoEM images of a similar reconstituted system of FtsZ plus FtsA inside membrane vesicles. Their proteins were from Thermotoga maritima, whose FtsA is well behaved in vitro. FtsZ was assembled into long pfs that associated in pairs and triplets (Fig. 5.5b). Favorable projections showed a dot between FtsZ and the membrane, which was interpreted as an FtsA filament in cross section. The FtsZ filaments formed arcs, with a diameter of ~100 nm, at various locations on the membranes. At sites of constriction the FtsZ pf pairs and triplets encircled the liposome, with a zone of overlap after completing the circuit. The maximum constriction observed was about 90 nm in diameter, consistent with the intermediate curved conformation.

Fig. 5.5.

Panel A shows a section through a cryoEM tomogram of Z rings reconstituted from FtsZ plus FtsA. The left side of the vesicle shows two Z rings in oblique section. They each comprise ribbons of pfs spaced ~7.5 nm apart. Panel B shows a projection of a an entire vesicle, with ribbons of 3 and 4 protofilaments forming arcs encircling sites of constriction (Reprinted from Szwedziak et al. 2014, with permission of the authors. a was extracted from their video 4, b is their Fig. 5.3c)Panels C and D show negative stain images of inside-out Z rings of mts-FtsZ, reconstituted on rigid lipid tubules. The dark stained Z rings comprise ribbons of parallel, close-packed pfs. The Fourier analysis (inset d) indicates a uniform 5 nm spacing of pfs (Reprinted from Milam et al. 2012 with permission of the authors). Scale bars are 100 nm (a, b) 500 nm (c) and 200 nm (d)

Loose and Mitchison (2014) reconstituted FtsZ plus FtsA, not in liposomes but on planar lipid bilayers, using fluorescently tagged proteins that could be observed over time. Their proteins were from E. coli, and they obtained stable wild type FtsA by a SUMO fusion and expression at 18 °C. A 3:1 mixture of FtsZ:FtsA was placed over a planar lipid bilayer on a glass coverslip, and after ~5 min the adsorbed protein organized into rings, with a diameter of ~1.2 μm. The rings were ~0.5 μm thick, so they were clearly bundles or toroids of many pfs. Remarkably, the toroids showed rotational movement with a velocity of 110 nm/s = 25 subunits/s. (That is very fast, five times faster than the elongation rate of single pfs in solution at a steady state subunit concentration of 1 μM (Chen and Erickson 2005).) When single fluorescent molecules were sparsely doped they remained stationary for an average 7 s lifetime, which suggests that the mechanism driving the motion is subunit exchange, perhaps treadmilling, rather than sliding of pfs relative to each other. Because the bundle moves in one direction, rather than sliding apart, the pfs in the bundles or toroids must be arranged in a parallel fashion, all facing the same direction.

Arumugam et al. (2014) did a similar reconstitution on planar lipid bilayers, but they used FtsZ-mts without FtsA. The FtsZ-mts assembled small filament bundles, mostly straight, that grew longer and eventually anastomosed into a network. Although this network appeared stable, FRAP showed that it was rapidly exchanging subunits with a half time of 10 s, similar to the rate of exchange in the Z ring in vivo (Anderson et al. 2004) and single pfs in solution (Chen and Erickson 2005). Importantly, the exchange did not result in new pf bundles but took place within the existing bundles. This suggests that there are multiple pf ends within the bundles where exchange takes place. MinC was shown to disassemble the bundle network, apparently by first binding to these ends. The authors then reconstituted the MinCDE system and showed that the waves of peak Min resulted in disassembly of FtsZ, which reassembled at the Min trough.

The FtsZ polymers assembled on planar lipid bilayers are wider than the 250 nm resolution of the light microscope, whether tethered by FtsA or directly by the –mts. They have been termed “bundles,” which implies a 3D structure, but they may actually be ribbons, one subunit thick, in which every pf is tethered to the membrane. It should be possible to resolve this question by negative stain or cryoEM. This may also address the discrepancy, discussed below, of the 7–9 nm pf spacing seen in reconstitution of FtsZ plus FtsA (Szwedziak et al. 2012), vs. the 5 nm spacing in ribbons of mts-FtsZ (Milam and Erickson 2013).

Sliding pfs – Do They Generate Constriction or Just Accommodate It?

The sliding-filament model of constriction force (Hörger et al. 2008; Lan et al. 2009) proposed that the Z ring is a long filamentous structure that can span the circumference of the cell, with the two ends meeting in an overlap zone where they can associate laterally. If the filaments could slide to increase the overlap, the increased lateral interaction should be thermodynamically favored, and this could generate constriction. This seems valid thermodynamically, but, as pointed out previously (Erickson 2009), this mechanism seems doomed by a kinetic trap. In order to slide, the filaments need first to break all lateral bonds, and as the number of lateral bonds increases, the time needed for complete rupture increases exponentially.

Although sliding itself is unlikely to generate a constriction force, sliding is probably essential to accommodate continued constriction. If the Z ring were only a partial circle, with a gap between the ends, constriction could continue until the gap closed. If a long pf pair made a complete circuit and the ends passed each other in an overlap zone (Szwedziak et al. 2014), continued constriction would require that the overlapping ends could slide. In this case it would be important that the overlap not have lateral bonds that would impose a brake on the sliding.

Consider next a model where a Z ring comprised four pfs, each of them making a complete circuit and then annealing to form a continuous circle. The complete circle would arrest constriction until a gap was created. We have suggested this model previously to explain the observation that Z rings reconstituted in GMPCPP generated an initial constriction, but then arrested (Osawa and Erickson 2011). This is in contrast to Z rings assembled in GTP, which continued constricting. Importantly, Z rings in GTP are constantly exchanging subunits between the Z ring and solution. Subunit exchange would necessarily create gaps, which would permit continued constriction until the gap is closed. Z rings assembled in GMPCPP do not exchange and would not create gaps, so constriction arrests.

Constriction Force by Partial Z Rings

Although FtsZ assembles complete circular Z rings in cells and in tubular liposomes, there are several examples of constriction force being generated without closure of the ring. The concave depressions generated on large liposomes probably contain only arcs of pfs, not a complete circle (Arumugam et al. 2012; Osawa et al. 2009). The E. coli mutant ftsZ26 forms spiral Z rings, and scanning EM showed spiral constrictions, demonstrating force generation without closure into a ring (Addinall and Lutkenhaus 1996). An impressive example of partial Z rings generating arcs of constriction has been documented for a plastid (Sato et al. 2009). Force generation by these partial Z rings is difficult to explain by active filament sliding.

The pf Substructure of Z Rings – Ribbons or Scattered?

In E. coli there are ~6700 molecules of FtsZ in the cell (Li et al. 2014)¹, and fluorescence assays have found that 30–40% of the total FtsZ is in the Z ring (Geissler et al. 2007; Stricker et al. 2002). The 2000–2700 FtsZ molecules in the Z ring could make a pf 8600–11,600 nm long, enough to encircle the 900 nm inside diameter three to four times. For shorter and longer cells this could be 2–5 circuits, which we take to be the average number of pfs across the width of the Z ring. There are two competing models for how pfs are arranged in the Z ring. In the ribbon model the 2–5 pfs are thought to be parallel and in lateral contact, making a ribbon 10–25 nm wide. In the scattered model the pfs more widely spaced and not in contact, creating a band ~100 nm or more wide. In both models all pfs are tethered to the membrane.

The scattered model was first suggested by a cryoEM study of C. crescentus, which showed short pfs scattered around the Z ring and only rarely in contact with each other (Li et al. 2007). Several studies by super-resolution light microscopy have indirectly supported this model by reporting widths of the Z ring ~110 nm (Biteen et al. 2012; Fu et al. 2010; Holden et al. 2014); a ribbon of 2–5 pfs should be only 10–25 nm wide. A recent PALM study of the Z ring in Streptococcus pneumoniae measured the axial width of the Z ring to be 95 nm early in the cell cycle, increasing to 127 nm as the Z ring constricted (Jacq et al. 2015). It should be noted, however, that the most recent and comprehensive PALM studies (Coltharp et al. 2016; Holden et al. 2014; Jacq et al. 2015) also measured the thickness of the Z ring in the radial direction. The radial thickness was very close in magnitude to the axial width (71 nm axial width vs. 64 nm radial thickness (Holden et al. 2014); Fig. 7 in (Jacq et al. 2015); 99 nm axial vs. 59 nm radial (Coltharp et al. 2016)). This large radial width contradicts our expectation that all pfs are tethered to the membrane by FtsA and ZipA, necesitating a Z ring that is radially one subunit thick. It is important to recall that in E. coli the Z ring averages only 2–5 pfs thick (both axial and radial), so there is not enough material to build in the radial direction. This suggests that the actual radial thickness should be ~5 nm. The large radial thickness measured in the PALM images may therefore reflect the achieved resolution (which is worse than the resolution predicted theoretically in the studies). Since the measured axial width was only 7–40 nm more than the radial, the actual axial width of the Z ring might well be as small as 10–25 nm. Overall, the super-resolution light microscopy does not provide convincing support for the larger width of the scattered model.

A recent cryoEM study by Szwedziak et al. (2014) provides strong support for the ribbon model in both C. crescentus and E. coli. Their tomograms showed parallel arrays of pfs encircling the cells at the constriction site; these were clearly ribbons, one pf thick radially, and with variable axial widths. Szwedziak et al. (2014) also presented clear images of FtsZ rings reconstituted in liposomes with FtsA (Fig. 5.5). A typical Z ring comprised a ribbon of 2, 3 or 4 pfs that formed a continuous helical loop around the constriction, with a zone of overlap. In all cases the ribbons were one pf thick, with all pfs apparently linked to the membrane by FtsA. This supports the more important observation of Z rings in bacteria, which are ribbons, one pf thick.

The Spacing of pfs in the Ribbons

Curiously, in the cryo-EM study of Szwedziak et al. (2014) the pfs were spaced about 7–9 nm apart in both the in vitro reconstitution, and in cells of C. crescentus and E. coli. The earlier cryoEM study of Li et al. (2007) reported widely scattered pfs in wild type C. crescentus, but upon overexpression of FtsZ they also found ribbons of parallel pfs. Importantly, the pfs in their reconstructions were spaced 7–9 nm apart (7 nm by our measurements from their figures, 9.2 nm reported in their Fourier analysis).

In a separate study, Milam et al. (2012) succeeded in imaging reconstituted Z rings of mts-FtsZ by negative stain EM. These inside-out Z rings appeared as bands of uniform density and width, encircling lipid tubules 300 nm in diameter (Fig. 5.5). The width of a given Z ring varied from ~15 nm to >100 nm, but was constant for a given Z ring, consistent with ribbons of three to tens of pfs. Fourier analysis indicated a pf spacing of 5 nm (Fig. 5.5D), similar to 2-D sheets assembled in DEAE dextran (Erickson et al. 1996). These images also support the ribbon model.

The cryoEM and the negative stain both support a ribbon model, but they differ in the pf spacing. The negative stain showed pfs in lateral contact, with a 5 nm spacing, while the cryoEM showed a spacing of 7–9 nm. The negative stain images should not be dismissed as artifactual (Szwedziak et al. 2014). Uranyl acetate is an extremely rapid protein fixative (Zhao and Craig 2003), and is generally considered as good as cryo for preserving protein structures at a 1–2 nm level (Ohi et al. 2004). A problem with the 7–9 nm spacing is that the FtsZ pf is maximally 5 nm wide, so the pfs in these cryoEM images are apparently not in contact with each other. No mechanism has been suggested for forces that would operate through 2–4 nm of solvent to bring the pfs together as parallel tracks, but keep them 2–4 nm apart. Nevertheless, the agreement of the two independent studies by cryoEM (Li et al. 2007; Szwedziak et al. 2014) makes a strong case that the pfs in vivo are indeed held at a separation of 7–9 nm. A potentially important clue is that the pfs in the cryoEM studies were tethered to the membrane by FtsA, whereas the pfs imaged by negative stain were directly attached to the membrane by the amphipathic helix on mts-FtsZ. This suggests that FtsA may enforce the larger separation of pfs. However, a mechanism for FtsA to bridge adjacent pfs is not obvious.

The pf Substructure of Z Rings – Continuous or Patchy?

A different point of controversy is whether the Z ring has a continuous or patchy structure. Both the cryoEM and the negative stain of reconstructed Z rings show continuous Z rings of mostly uniform width. CryoEM also showed a uniform width of Z rings in bacteria (Szwedziak et al. 2014). In contrast, most super-resolution light microscope studies have shown a patchy structure, where bright patches of FtsZ are separated by dim or dark zones apparently depleted of FtsZ. This was first reported for images obtained by structured illumination microscopy (SIM) (Strauss et al. 2012) and was confirmed in a more recent SIM study (Rowlett and Margolin 2014). A similar patchy structure was reported in two super-resolution studies using PALM, which is a completely different super-resolution technique (Holden et al. 2014; Jacq et al. 2015). It is not yet clear how to resolve the contradictory structures seen by EM and light microscopy.

Z-Ring Assembly and Initial Constriction

New Z-rings assemble in daughter cells as the mother cell is finishing septation. A recent PALM study followed the intensity of the Z ring through the cell cycle (Coltharp et al. 2016). With slow growth in M9 minimal medium, the Z-ring initially contained about 25% of the cell’s total FtsZ, and this increased to 30% by 90 min. There was no obvious remodeling, but an earlier FRAP analysis showed that the Z ring is rapidly exchanging subunits with the cytoplasmic pool, with a half time of 12 s (Buss et al. 2015), very similar to the 8 s exchange observed under faster cell growth (Anderson et al. 2004). The Z ring then persisted without obvious change until ~145 min, when constriction began. The constriction comprised two phases: in the first 35 min, FtsZ remained present at a constant intensity (~35% of the total) as the Z ring constricted from 1000 nm to 250 nm; during the next 11 min FtsZ disassembled as the septum progressed to closure.

We suggest that FtsZ is generating a constriction force on the inner membrane as soon as the Z ring is assembled and throughout the first 145 min, but that attachment of the membrane to the rigid peptidoglycan wall prevents any actual constriction. During this time the Z ring serves as a scaffold for assembly of downstream division proteins, which will remodel the peptidoglycan wall. Constriction finally begins when this remodeling permits the peptidoglycan to follow the force that the FtsZ is exerting on the membrane. Invagination continues until the FtsZ reaches the 250 nm diameter of the intermediate curved conformation, which is probably the limit of pf bending. We suggest FtsZ as the driving force for constriction, primarily because it has been demonstrated to generate constriction in liposomes, with sufficient force to invaginate thick-walled, multilamellar liposomes.

This scenario, and the primacy of FtsZ in generating the constriction force, has been questioned by Coltharp et al. (2016). They examined how mutations in either FtsZ or peptidoglycan synthesis affected the timing of constriction onset and the rate of septum closure. They found that both constriction onset and rate of septum invagination were not affected by the FtsZ84 mutant, which has reduced GTPase and exchange dynamics. In contrast, alterations in peptidoglycan synthesis affected both constriction onset and the rate of closure. They concluded that “septum closure is likely driven by septum synthesis rather than Z-ring contraction.”

The idea that peptidoglycan remodeling might provide the primary driving force for septation has a long history. In the extreme scenario, the ring of FtsZ is proposed to serve primarily as a docking site for the remodeling enzymes, and the constriction force is generated entirely by the inward remodeling of the peptidoglycan. This was largely discounted when FtsZ was discovered in mycoplasma and archaea, which have no peptidoglycan cell wall (Margolin et al. 1996; Wang and Lutkenhaus 1996a, b). Since FtsZ, but none of the other Fts proteins, are found in archaea, FtsZ was boosted as the prime candidate for generating the constriction. In bacteria with a peptidoglycan wall, peptidoglycan remodeling is still a candidate for contributing to the constriction force (Coltharp et al. 2016; Meier and Goley 2014), perhaps especially in the later stage. This remains an intriguing speculation; however, compelling evidence is lacking that peptidoglycan remodeling contributes to the constriction force.

The observations of Coltharp et al. (2016) are actually consistent with our model, where FtsZ is the primary source of constriction force. We suggest specifically that FtsZ84, although having reduced GTPase and dynamics, can still generate a constriction force that is more than sufficient to drive septum invagination. The onset of constriction is triggered by the onset of peptidoglycan remodeling, which is a chemical process that is probably independent of the force on the membrane. Likewise, the rate of septum invagination is probably limited, not by the force generated by FtsZ, but by the rate at which remodeling permits the peptidoglycan wall to follow the inner membrane. In the scenario we propose, septum invagination is driven by the constriction force of FtsZ, but its rate is limited by the peptidoglycan remodeling, which allows the wall to follow passively.

The Final Step of Septum Closure

The final step of septation must involve the advancing furrow constricting to the point where the curved membranes contact and fuse into separate membranes of the daughter cells. FtsZ apparently does not participate in this final step. The intermediate curved pfs could constrict the furrow to a diameter of ~250 nm, but something else is needed to finish septation. In a recent study Söderstrom et al. (2014) used a clever FRAP assay to distinguish daughter cells still connected by a narrow gap, versus cells separated by the completed septum. They found that FtsZ disappeared from the Z ring before the septum was closed. In contrast, FtsA and downstream proteins that remodel the peptidoglycan remained longer, and were typically still present when the septum was closed. This was confirmed in the recent PALM study of Coltrap et al. (2016), which found that the FtsZ intensity in the Z ring remained constant as it constricted to ~250 nm diameter, and then the FtsZ disassembled.

An attractive general mechanism for the final stage of septum closure is excess membrane synthesis. As a septum ingresses, new membrane is needed to provide the increased surface area. If the cell synthesizes membrane in excess of the minimum, the excess will be accommodated most easily at the highly curved invaginating septum. Thus, if the FtsZ ring generated constriction to a diameter of ~250 nm, and the remodeled peptidoglycan maintained this constriction after the FtsZ dissociated, a small excess of membrane synthesis could drive the constriction to septum closure and force membrane fusion. An important consideration is that the membrane at the septum has two points of high curvature: where the septum meets the cell membrane, and at the tip of the constriction. These points of curvature are more favorable for membrane expansion than starting a new bud. Membrane expansion would be essential to accommodate the invaginating septum, but once the curvature is established it should also be sufficient to drive the membranes together for the final closure and fusion.

The potential for excess membrane synthesis to drive cell division was demonstrated in a recent study of Mercier et al. (2013). In a previous study from the Errington lab, Leaver et al. (2009) had created B. subtilis L forms, which had no peptidoglycan wall. These cells propagated, but surprisingly they did not even need FtsZ. They divided by extruding pseudopods, which spontaneously resolved by breaking up into small spherical cells. The following study by Mercier et al. (2013) showed that for the L forms to propagate, it was essential to provide a mutation or manipulation that generated excess membrane synthesis. The authors concluded that the original life form may have relied on this simple mechanism for cell division – excess membrane synthesis and membrane fluctuations leading to vesicles pinching off. We suggest that this may still be the mechanism for the final step of septation in modern bacteria.

In summary, we suggest that FtsZ provides the primary constriction force for cytokinesis by exerting a bending force on the inner membrane. Actual constriction only begins when peptidoglycan remodeling permits the cell wall to follow the membrane. Bending pfs then constrict the inner membrane to the ~250 nm diameter of the intermediate curved pfs. The peptidoglycan wall follows by remodeling, and this remodeling limits the speed of septum invagination. The final steps of membrane closure extension and fusion of the two peptidoglycan cell walls completes the septation are driven by excess membrane synthesis, fluctuations and fusion.

Table 5.1.

Copy number of cell division and cytoskeleton proteins, determined by Li et al. (2014)

Gene	MOPS complete	MOPS minimal	MOPS complete
			Without methionine
ftsA	984	575	1013
ftsB	487	140	173
ftsE	967	320	649
ftsI	349	144	226
ftsK	508	213	376
ftsL	416	201	423
ftsN	871	269	405
ftsP	905	196	410
ftsQ	336	147	172
ftsW	293	117	169
ftsX	838	244	436
ftsZ	6750	3335	5290
zipA	2128	501	874
minC	857	364	575
minD	5358	2444	3324
minE	3597	1970	2680
matP	601	360	347
slmA	2323	568	952
zapA	2275	738	2008
zapB	34,197	7797	18,090
ZapC/YcbW	155	155	155
ZapD/YacF	1983	373	538
ZapE/YhcM	255	214	262
mreB	11,304	2393	5570
mreC	738	176	333
mreD	367	71	148
rodZ	1309	576	669

This study used ribosome profiling to determine the rate of translation of 95% of the proteins in E. coli. The rates were converted to number of protein molecules synthesized in one cell cycle. Assuming no unusual degradation, the numbers can be taken as the average number of molecules per cell. The E. coli strain MG1655 was grown at 37 °C in three different media with different doubling times: 21.5 and 56.3 min in MOPS complete and incomplete media, and 26.5 min in MOPS complete without methionine. The latter condition required the cell to substantially upregulate the met-E enzyme, altering overall metabolism. We have extracted cell division and cytoskeleton proteins from their table S1. It seems quite valuable to have these numbers determined for all proteins in the identical cell and growth conditions. The 6750 molecules of FtsZ in a cell volume of 2 × 10⁻¹⁵ L is 5.6 μM