Model-Fusion-Based Online Glucose Concentration Predictions in People with Type 1 Diabetes

Abstract

Accurate predictions of glucose concentrations are necessary to develop an artificial pancreas (AP) system for people with type 1 diabetes (T1D). In this work, a novel glucose forecasting paradigm based on a model fusion strategy is developed to accurately characterize the variability and transient dynamics of glycemic measurements. To this end, four different adaptive filters and a fusion mechanism are proposed for use in the online prediction of future glucose trajectories. The filter fusion mechanism is developed based on various prediction performance indexes to guide the overall output of the forecasting paradigm. The efficiency of the proposed model fusion based forecasting method is evaluated using simulated and clinical datasets, and the results demonstrate the capability and prediction accuracy of the data-based fusion filters, especially in the case of limited data availability. The model fusion framework may be used in the development of an AP system for glucose regulation in patients with T1D.

1. Introduction

Type 1 diabetes (T1D) is a chronic disease that is characterized by the inability of the pancreas to produce insulin required for the regulation of blood glucose concentration (BGC). People with T1D must administer exogenous insulin to maintain their BGC within the desired range (70–180 mg/dL). If BGC is not tightly regulated, the glycemic excursions may cause hypoglycemia (low BGC) or hyperglycemia (high BGC), which may lead to a variety of hazardous, long-term complications (Centers for Disease Control and Prevention 2011).

To mitigate hypo- and hyperglycemic excursions, closed-loop AP systems that incorporate continuous glucose sensors, insulin pumps, and appropriate control algorithms have been developed to automatically calculate and administer the required insulin dosage. A hybrid AP has been announced with availability in 2017 (Garg et al. 2017). However, the conventional AP systems typically involve proportional-integral-derivative control techniques that ordinarily rely on the current glucose measurements and a rudimentary model of the glucose-insulin dynamics (Percival et al. 2008). The recent development of accurate continuous glucose monitoring (CGM) systems have increased interest in the predictive modeling of glucose concentrations, which is useful in hypo- and hyperglycemic early warning alarms (Chico et al. 2003) and model-based predictive control in advanced AP systems (Hovorka et al. 2004, Cobelli et al. 2009, Ellingsen et al. 2009, Kovatchev et al. 2009, Dassau et al. 2010, Pappada et al. 2011, Bequette 2012, Cobelli et al. 2012, Eren-Oruklu et al. 2012, Haidar et al. 2013, Jacobs et al. 2014, Kirchsteiger et al. 2015, Kovatchev et al. 2016, Haidar et al. 2017, Turksoy et al. 2017, Wang et al. 2017). Nevertheless, accurately predicting the future glucose trajectories is a challenging problem as BGC is influenced by several factors including meals, administered insulin, exercise (Diabetes Research in Children Network Study Group 2005, Breton et al. 2014, Peyser et al. 2014, DeBoer et al. 2016, Jacobs et al. 2016, Turksoy et al. 2016a, Turksoy et al. 2016b, Pasieka et al. 2017, Turksoy et al. 2017) and emotional state (related to the concentration of certain hormones) (Nomura et al. 2000). Moreover, different physiological phenomena and the diverse lifestyles of individuals result in significant variability in glucose dynamics over time and among patients (Brazeau et al. 2008). These causes of glucose variability pose substantial challenges for the accurate prediction of future glucose trajectories.

To address this problem, previous research studies (Parker et al. 1999, Reifman et al., Gani et al. 2010, Pérez-Gandía et al. 2010, Nixon and Pickup 2011, Pappada et al. 2011, Zhao et al. 2011, Eren-Oruklu et al. 2012, Turksoy et al. 2014, Zhao et al. 2014, Kirchsteiger et al. 2015, Zhao and Yu 2015) have utilized various types of models for BGC prediction (or even development of AP systems) that can generally be divided into two main categories: physiological models and data-driven empirical models. Physiological models describe the glucose dynamics based on the fundamental understanding of the biological and chemical phenomena. Despite the abundant use of physiological models (Bergman 1989, Lehmann and Deutsch 1992, Parker et al. 1999, Parker et al. 2000, Hovorka et al. 2004), it may be difficult to develop a model that is personalized to individual patients because the model parameters may not be readily estimated from the limited measurements available (Dalla Man et al. 2016, Messori et al. 2016, Piccinini et al. 2016, Visentin et al. 2016, Toffanin et al. 2017). Daily adaptation of physiological model was proposed recently (Dalla Man et al. 2016, Messori et al. 2016, Piccinini et al. 2016, Visentin et al. 2016, Toffanin et al. 2017). Alternatively, data-driven models offer a simpler structure that is sufficient for online prediction yet computationally tractable for online and adaptive estimation, thus able to capture the time-varying relationships among the system variables (Cherkassky and Mulier 2007, Araghinejad 2013, Wang et al. 2013, Turksoy et al. 2014, Cinar et al. 2016, Turksoy et al. 2016a, Turksoy et al. 2016b, Turksoy et al. 2017). Once such relationships are identified, they can be used to train models that complement or replace physiological models.

In general, empirical models predict the future glucose values based on a combination of either the predicted or measured current and historical glucose signals. Such types of models can be divided into linear and nonlinear models. For linear models, AR (autoregressive) or ARX (autoregressive with exogenous inputs) modeling methods were developed by using the current and previous BG values or adding exogenous inputs. Since these models usually consider the output predictions to be a linear combination of the model inputs, the model parameters can be readily updated online. The advantages of using linear methods are simplicity, computational tractability, and rapid convergence of the model parameters without the onerous demands of requiring abundant training data. The disadvantage is that, for more reliable prediction results, the ARX models need information that cannot be captured or computed autonomously in real time applications (such as carbohydrate content of meals, concentration of some hormones, etc.). For nonlinear modeling approaches, a large training dataset is typically required to characterize the nonlinear temporal dynamics of blood glucose metabolism, while the learning algorithms may be more time-consuming and computationally expensive. However, a personalized nonlinear dynamic model may result in more accurate predictions, provided the training data are sufficient to identify the nonlinear relationships.

A recent trend is to construct a hybrid data-driven model (Azmi et al. 2010) through the combination of various model types (linear/nonlinear or AR/ARX) obtained from different modeling algorithms (See and Abrahart 2001). Nevertheless, an inherent challenge of designing the BGC predictor through hybrid models is to ensure that different data-driven models are appropriately combined and coordinated with a suitable decision-making mechanism. Along this direction, recent work (Stahl et al. 2012) used a probabilistic framework approach to combine three parallel predictors using a soft switcher derived from the Bayesian model averaging technique to find the best individual predictor.

Motivated by the above considerations, an online data-driven prediction strategy is proposed in this work that employs filtering fusion and a decision-making mechanism for accurate glucose concentration predictions in people with T1D. Considering the complexities of glucose dynamics, it is not practical to develop a universal/global prediction model for all subjects. A more suitable approach is to train a personalized model using present and historical data from CGM sensors. Since the characteristics of various kinds of adaptive filters may be better suited to different dynamic processes, training sizes, time-variant and noise environments, the filter fusion methodology is utilized and the parameters of each filter are appropriately designed so that the overall combinational filter can be used in various situations for online glucose prediction. The linear adaptive filters (recursive least squares [RLS] and extended recursive least squares [EX-RLS]) generally require less data for updating the model parameters than the nonlinear kernel-based filters (kernel recursive least squares [KRLS] and extended kernel recursive least squares [EX-KRLS]) (Liu et al. 2011). However, kernel-based filters usually have better prediction results than the linear filters if the data are inherently nonlinear. Furthermore, a decision-making mechanism for filter fusion is proposed based on different prediction performance indices to guide the overall output of the filter to have better prediction accuracy than the individual filters. The accuracy of the proposed predictor is demonstrated by predicting the glucose measurements of in silico and clinical subjects. The performance of fusion filtering method is also compared with each of the adaptive filtering models for short-term (5–30 min) online glucose prediction. The rest of this paper is organized as follows. Section 2 outlines the four adaptive filtering algorithms and analyzes their characteristics. Then, a detailed description of the model selection and filtering fusion mechanism for online glucose prediction is developed. Section 3 contains the description of the computational experiments and the accompanying results. Section 4 presents the highlights of the experiments as well as a discussion of the findings. Section 5 concludes the paper.

2. Methodology

2.1 Hybrid models with different adaptive filtering algorithms

To improve the accuracy of online prediction, adaptive filters (Goodwin and Sin 2014), various candidate models with unique and distinguished characteristics are applied to obtain candidate data-driven models. Based on the complex features of the glucose dynamics, recursive least squares (RLS) (Haykin 2008), extended recursive least squares (EX-RLS) (Sayed 2003), kernel recursive least squares (KRLS) (Engel et al. 2004) and extended kernel recursive least squares (EX-KRLS) (Liu et al. 2009) are selected for training the candidate models.

RLS is a well-known linear regression algorithm which follows the Wiener solution at each iteration (Sayed 2003). EX-RLS provides a state-space model and variant hidden states, which can improve the tracking performance of RLS and model uncertainty (Liu et al. 2009). To solve nonlinear adaptive filtering problems, kernel methods have been proposed recently (Aronszajn 1950, Liu et al. 2011) that formulate nonlinear functions in terms of inner products in high-dimensional reproducing kernel Hilbert spaces (RKHS). Therefore, linear adaptive filter algorithms can be constructed in the kernel feature space obtained by mapping the original CGM measurements to a high-dimensional feature space via appropriate kernel functions. KRLS is such a kernel variant algorithm of RLS that can approximate online the underlying nonlinear function based on the training dataset. EX-KRLS is another kernel version of EX-RLS that has the theoretic framework to deal with nonlinear state-space model estimation (Liu et al. 2009). Furthermore, EX-KRLS improves upon the capability of KRLS model, thus EX-KRLS is able to handle the small variations or slow drift issues in the nonlinear data. These four adaptive filter algorithms are proposed in this section as the basis of developing candidate models. Then, their characteristics are compared to develop a reasonable fusion mechanism.

In an autoregressive model, an output signal d(i) at the ith iteration can be expressed as a linear combination of historically observed signals

$$d(i)=\mathbf{u}{(i)}^T\mathbf{w}(i)+\upsilon (i)(i)$$ (1)

where u(i) is the input vector at the ith iteration, w(i) represents the weights to be estimated, and ν(i) denotes the random white noise in the process.

RLS finds the weight vector w that best represents the correlations in the desired output d(i). With regards to state-space model formulations, RLS can be written in a the mathematically equivalent form (Haykin 2008)

$$\begin{array}{c}\mathbf{x}(i+1)=\mathbf{x}(i)\\ d(i)=\mathbf{u}{(i)}^T\mathbf{x}(i)+\upsilon (i)\end{array}$$ (2)

where the state vector x(i) is constant and the optimal weights w(i), which need to be learned from the training data {d(i),u(i)} at the ith iteration, are unable to track time-varying trajectories.

To solve this problem, the EX-RLS approach has a more general linear state-space model and variant hidden states (Haykin 2008)

$$\begin{array}{c}\mathbf{x}(i+1)=\mathbf{\text{Ax}}(i)+{\upsilon }_1(i)\\ d(i)=\mathbf{u}{(i)}^T\mathbf{x}(i)+{\upsilon }_2(i)\end{array}$$ (3)

where A denotes the state transition matrix, ν₁(i) represents the state noise and ν₂(i) is the observation noise. By using the EX-RLS algorithm, the tracking performance of a process with time-varying parameters can be improved effectively.

For a nonlinear process, Mercer theorem is used (Aronszajn 1950) to compute RLS and EX-RLS models in the feature space to transform the input vector u(i) into the RKHS as φ(u(i)), described as φ(i), and formulate regression algorithms on the sequence {d(i),φ(i)}. Then for a newly available input-output pair {d(i),u(i)}, the optimal weights w(i) at the ith iteration are computed such that the weights minimize a specific cost function. Table 1 summarizes different model structures and cost functions of the four algorithms (Liu et al. 2009).

Table 1.

summary of different state space models and cost functions of the four algorithms.

Algorithms	Models	Cost functions
RLS	x(i + 1) = x(i) d(i) = u(i)Tx(i) + υ(i)	$\underset{\mathbf{w}}{min}\sum _{i=1}^i{\beta }^{i-j}{|d(j)-\mathbf{u}{(j)}^T\mathbf{w}|}^2+{\beta }^i\lambda {\Vert \mathbf{w}\Vert }^2$
EX-RLS	x(i + 1) = Ax(i) + υ1(i) d(i) = u(i)Tx(i) + υ2(i)	$\begin{array}{c}\underset{\{\mathbf{x}(1),{\upsilon }_1(1),\dots ,{\upsilon }_i(i)\}}{min}[\sum _{j=1}^i{\beta }^{i-j}{|d(j)-\mathbf{u}{(j)}^T\mathbf{x}(j)|}^2+\lambda {\beta }^i{\Vert \mathbf{x}(1)\Vert }^2+q^{-1}\sum _{j=1}^i{\beta }^{i-j}{\Vert {\upsilon }_1(j)\Vert }^2],\\ \text{subject to}\mathbf{x}(j+1)=\mathbf{\text{Ax}}(j)+{\upsilon }_1(j),\end{array}$
KRLS	x(i + 1) = x(i) d(i) = φ(i)Tx(i) + υ(i)	$\underset{\mathbf{\omega }}{min}\sum _{j=1}^i{\beta }^{i-j}{|d(j)-{\mathbf{\omega }}^T\mathbf{\phi }(j)|}^2+{\beta }^i\lambda {\Vert \mathbf{\omega }\Vert }^2$
EX-KRLS	x(i + 1) = αx(i) + υ(i) d(i) = φ(i)Tx(i) + υ2(i)	$\begin{array}{c}\underset{\{\mathbf{x}(1),{\upsilon }_1(1),\dots ,{\upsilon }_i(i)\}}{min}[\sum _{j=1}^i{\beta }^{i-j}{|d(j)-\mathbf{\phi }{(j)}^T\mathbf{\omega }(j)|}^2+\lambda {\beta }^i{\Vert \mathbf{\omega }(1)\Vert }^2+q^{-1}\sum _{j=1}^i{\beta }^{i-j}{\Vert {\upsilon }_1(j)\Vert }^2],\\ \text{subject to}\mathbf{x}(j+1)=\alpha \mathbf{x}(j)+{\upsilon }_1(j),\end{array}$

For the state-space model of EX-RLS, A is the state transition matrix. In the identification process, the state variables are considered as time-invariant (identified by RLS or KRLS) or very slow time-variant (identified by EX-based filters). Therefore, the matrix A is considered as the unit matrix in the RLS/KRLS algorithms. For EX-KRLS, α is a scaling factor that indicates a unidirectional change in the state (A = αI). If the model shows a slow process with time-varying parameters, the factor α can be set close to 1. Moreover, ω = [ω₁, ω₂,…, ω_n]^T is the coefficient vector, and λ is the regularization parameter to control the initial state vector norm in the cost functions, β is the forgetting factor to incorporate an exponential weighting on the past data and q is proportional to the state noise variance that provides trade-off between the measurement disturbance and modeling variation. Therefore, state noise can be excluded by setting q = 0, and with α = 1 the EX-based algorithms will be degraded to the conventional RLS/KRLS algorithms. Further, φ(i) is a transformation of the input vector u(i) into the RKHS as given by Mercer's theorem, and can be readily calculated by a kernel function.

The cost functions of EX-RLS and EX-KRLS are more complex quadratic optimization problems with linear constraints compared to the constraint-free cost functions of RLS and KRLS (Table 1). The optimization problems in Table 1 do not need to be solved directly at each sampling instance. Rather, the weights can be calculated recursively from their previous estimate without explicitly solving any optimization. Table 2 presents the recursive procedure for updating weights in the four adaptive filtering techniques.

Table 2. Summary of correlated adaptive filtering algorithms.

Algorithm 1: RLS	Algorithm 2: EX-RLS
Initialization w(0) = 0, P(0) = λ−1I	Initialization w(0) = 0, P(0) = λ−1I
Iterate for i ≥ 1 $\begin{array}{c}r(i)=1+{\beta }^{-1}\mathbf{u}{(i)}^T\mathbf{P}(i-1)\mathbf{u}(i)\\ \mathbf{k}(i)={\beta }^{-1}\mathbf{P}(i-1)\mathbf{u}(i)/r(i)\\ e(i)=d(i)-\mathbf{u}{(i)}^T\mathbf{w}(i-1)\\ \mathbf{w}(i)=\mathbf{w}(i-1)+\mathbf{k}(i)e(i)\\ \mathbf{P}(i)={\beta }^{-1}\mathbf{P}(i-1)-\mathbf{k}(i)\mathbf{k}{(i)}^{T}r(i)\end{array}$	Iterate for i ≥ 1 $\begin{array}{c}{r}_e(i)={\beta }^i+\mathbf{u}{(i)}^T\mathbf{P}(i-1)\mathbf{u}(i)\\ {\mathbf{k}}_p(i)=\mathbf{A}\mathbf{P}(i-1)\mathbf{u}(i)/r_e(i)\\ e(i)=d(i)-\mathbf{u}{(i)}^T\mathbf{w}(i-1)\\ \mathbf{w}(i)=\mathbf{A}\mathbf{w}(i-1)+{\mathbf{k}}_p(i)e(i)\\ \mathbf{P}(i)=\mathbf{A}[\mathbf{P}(i-1)-\mathbf{P}(i-1)\mathbf{u}(i)\mathbf{u}{(i)}^T\mathbf{P}(i-1)/r_e(i)\mathbf{]}{\mathbf{A}}^T+{\beta }^{i}q\mathbf{I}\end{array}$
Algorithm 3: KRLS	Algorithm 4: EX-KRLS
Initialization $\begin{array}{c}\mathbf{Q}(1)={(\lambda +\kappa (\mathbf{u}(1),\mathbf{u}(1)))}^{-1}\\ \mathbf{a}(1)=\mathbf{Q}(1)\mathbf{d}(1)\end{array}$	Initialization $\begin{array}{ccc}a(1)=\frac{\alpha d(1)}{\lambda \beta +\kappa (\mathbf{u}(1),\mathbf{u}(1)};& {\rho }_r(1)=\frac{\lambda \beta }{{\left|\alpha \right|}^2\beta +\lambda q};& \mathbf{Q}(1)=\\ {\left|\alpha \right|}^2/(\lambda \beta +\kappa (\mathbf{u}(1),\mathbf{u}(1)))({\left|\alpha \right|}^2+\beta \lambda q)\end{array}$
Iterate for i ≥ 1 $\begin{array}{c}\mathbf{h}(i)={[\kappa (\mathbf{u}(i),\mathbf{u}(i)),\dots ,\kappa (\mathbf{u}(i),\mathbf{u}(i-1))]}^T\\ \mathbf{z}(i)=\mathbf{Q}(i-1)\mathbf{h}(i)\\ r(i)=\lambda +\kappa (\mathbf{u}(i),\mathbf{u}(i))-\mathbf{z}{(i)}^T\mathbf{h}(i)\\ \mathbf{Q}(i)=r{(i)}^{-1}\left[\begin{array}{cc}\mathbf{Q}(i-1)r(i)+\mathbf{z}(i)\mathbf{z}{(i)}^T& -\mathbf{z}(i)\\ -\mathbf{z}{(i)}^T& 1\end{array}\right]\\ e(i)=d(i)-\mathbf{h}{(i)}^T\mathbf{a}(i-1)\\ \mathbf{a}(i)=\left[\begin{array}{c}a(i-1)-\mathbf{z}(i)r{(i)}^{-1}e(i)\\ r{(i)}^{-1}e(i)\end{array}\right]\end{array}$	Iterate for i ≥ 1 $\begin{array}{c}\mathbf{h}(i)={[\kappa (\mathbf{u}(i),\mathbf{u}(i)),\dots ,\kappa (\mathbf{u}(i),\mathbf{u}(i-1))]}^T\\ \mathbf{z}(i)=\mathbf{Q}(i-1)\mathbf{h}(i)\\ r(i)=\lambda +\kappa (\mathbf{u}(i),\mathbf{u}(i))-\mathbf{z}{(i)}^T\mathbf{h}(i)\\ e(i)=d(i)-\mathbf{h}{(i)}^T\mathbf{a}(i-1)\\ \mathbf{a}(i)=\alpha \left[\begin{array}{c}\mathbf{a}(i-1)-\mathbf{z}(i)r{(i)}^{-1}e(i)\\ r{(i)}^{-1}e(i)\end{array}\right]\\ {\rho }_r(i)={\rho }_r(i-1)/[{\left|\alpha \right|}^2+{\beta }^{i}q{\rho }_r(i-1)]\\ \mathbf{Q}(i)=\frac{{\left|\alpha \right|}^2{\rho }_r(i)}{r(i){\rho }_r(i-1)}\left[\begin{array}{cc}\mathbf{Q}(i-1)r(i)+\mathbf{z}(i)\mathbf{z}{(i)}^T& -\mathbf{z}(i)\\ -\mathbf{z}{(i)}^T& 1\end{array}\right]\end{array}$

In Table 2, the weight vector w(i) for the ith iteration is updated from the last estimate of the weights based on a correction factor that is directly proportional to both the prediction error for the observation d(i), denoted e(i), and the gain vector, denoted k(i). Furthermore, the matrix P(i) of dimension L×L is the inverse of the data autocorrelation matrix, and β is called the forgetting factor (usually specified close to 1), λ is the regularization parameter to control the initial state vector norm in the cost functions, and q indicates the trade-off between the measurement error and state noise. The parameter α is a scaling factor, which indicates a uni-directional change in state. Thus, if the system dynamics evolve gradually over time, α is close to 1. Furthermore, a represents the parametrization of the weights ω = [ω₁, ω₂,…, ω_n]^T, while Q and ρ_r are used to parameterize the matrix P for the development of the computational tractable recursive algorithms. One advantage of the recursive least squares algorithms is that they compute updated weights at each iteration, which is appealing for the artificial pancreas application where CGM measurements are available at each sampling instance. A framework for combining the various candidate models is presented next.

2.2 Model selection and filtering fusion mechanism

Developing hybrid or multiple models is an effective approach to leverage the strengths of each model while mitigating their respective drawbacks. This subsection focuses on the fusion mechanism of the multi-model approach, which combines the four data-driven models presented.

For improving the capability of the combined models and designing a proper fusion mechanism, it is necessary to provide an overview and summarize the different features (strengths and weaknesses) of each candidate model. Each model was analyzed to evaluate its strengths and weaknesses, such as the ability to model nonlinear systems and multivariate systems, and the uncertainty of processes for instance. Furthermore, the simplicity and ease of calibration of the models and their complexity of formulation are other important characteristics that are considered when evaluating the strengths or limitations of the models. Table 3 provides a comparative analysis of the four candidate models using various evaluation criteria (Sayed 2003, Liu et al. 2008, Liu et al. 2009, Liu et al. 2011, Araghinejad 2013).

Table 3. Comparison of candidate models.

Models	Strengths	Weaknesses
RLS	Simplicity of calibration; Generalization; Rapid convergence; Better performance for limited training data;	Poorer tracking performance for process with time-varying parameters; Disability for nonlinear process; (with respect to the other three methods)
EX-RLS	Good tracking performance for linear process with time-varying parameters; Applicable to model uncertainty;	Lack of flexibility; Disability for nonlinear process; Sensitive to parameters;
KRLS	Ability to represent nonlinear problems;	Computation complexity increases with the training data size; Need more training data to approximate a nonlinear process;
EX-KRLS	Better tracking performance for dynamic nonlinear process; Ability of estimating nonlinear state space model; Ability of modeling nonlinear systems with slow time-variant states;	Computation complexity increases with the training data size; More training data is needed to approximate the nonlinear process; Sensitive to parameters; Too complex in case of the model order is higher;

In Table 3, “simplicity of calibration” gains further importance and preference over other models in situations where the prediction accuracy of the models is relatively similar. “Generalization” refers to the ability of the models to perform well in both extrapolation and interpolation circumstances, and to be readily employed in calibration and validation studies (Araghinejad 2013).

When considering the task of predicting BGC values online, it is not trivial to settle on a specific model structure that suits the diverse and often competing expectations such as accurate predictions and computational efficiency. Further complicating the model selection is the fact that the prediction error is highly sensitive to time-varying dynamics of the process. In addition, at the initialization of the training phase, the data available for identifying the model parameters is often limited. Therefore, linear filtering algorithms such as RLS and EX-RLS may provide better results initially. However, as more data are collected online and a sufficient quantity of data becomes available for model training, the kernel versions of the algorithms may offer better performance. To increase prediction accuracy, the fusion mechanism is proposed that can effectively combine the various models based on certain indexes.

To develop the hybrid model, each candidate data-driven model is described by the following equation:

$$y(i)=f(\mathbf{x}(i))+\varepsilon (i)$$ (4)

To address the problem of online prediction, equation (4) can be represented by considering similar inputs as the following matrix form (Araghinejad 2013):

$$\widehat{y}(i)=\left[\begin{array}{c}{y}_1(i)\\ y_2(i)\\ ⋮\\ y_m(i)\end{array}\right]=\left[\begin{array}{c}{f}_1(\mathbf{x}(i))\\ f_2(\mathbf{x}(i))\\ ⋮\\ f_m(\mathbf{x}(i))\end{array}\right]+\left[\begin{array}{c}{\varepsilon }_1(i)\\ {\varepsilon }_2(i)\\ ⋮\\ {\varepsilon }_m(i)\end{array}\right]$$ (5)

where ŷ(i) is the matrix of y(i) combined by different candidate models and m is the number of models that can be used to predict y(i). According to the data fusion scheme, ŷ(i) can be calculated through the linear weighted method of each estimation of y(i):

$$\widehat{y}(i)={\mathbf{w}}^T\widehat{y}(i)=\sum _{j=1}^m{w}_j{y}_j(i)$$ (6)

To update the combination weights w, the stack method (Shu and Burn 2004) is used to find the optimal weight vector

$$\begin{array}{c}min\sum _{j=1}^m{[\widehat{y}(i)-w_j{y}_j(i)]}^2\\ \mathit{\text{subject}}:\sum _{j=1}^m{w}_j=1\end{array}$$ (7)

For robustness and efficiency considerations in online BGC prediction, all four prediction models developed by different adaptive algorithms are not employed simultaneously in the hybrid model. Rather, two of them are chosen through two specific criteria. “Criterion 1” is designed to find the prediction model with the lowest mean value of the prediction error. In this way, the filtering algorithm with the best transient performance will be selected. “Criterion 2” is designed to find the prediction model with the lowest learning error with the certain sliding window of past training samples. Therefore, the model with the best fit (while avoiding overfitting) in current dynamic process will be selected for the following convex combination. Meanwhile, the stack method is used to update the combination weights for these two candidate models. Therefore, the fusion result could be calculated via a linear weighted method, and the overall online prediction of BGC value will be obtained through a smoothing filter to avoiding abrupt fluctuations. The flowchart in Figure 1 describes the details of the combination mechanism for incorporating the output from the candidate models to provide a final prediction output.

Figure 1.

Flowchart of multi-model data fusion procedure for online prediction.

The flowchart of hybrid prediction procedure based on fusion mechanism is shown in Figure 1. First, the observed value x(i) from the i-th iteration CGM signal is obtained, providing a new input vector x(i) as well as a desired value for the short-term previous prediction ỹ(i). For four candidate models developed by RLS, EX-RLS, KRLS, EX-KRLS, four prediction results and their error evaluations are provided for further selection. Then, according to the design criteria evaluating aspects of prediction error and learning error, two optimal prediction outputs are fused through the linear weighted method. The parameters of convex combination are updated by the slack method. Finally, for avoiding noise variations in the time-variant model identification, an additional filter is applied to smooth the prediction outputs to mitigate the noise and abrupt variability.

2.3 In Silico/Clinical Subjects and Evaluation Criteria

2.3.1 In Silico Subjects

For in silico evaluation, the FDA-approved UVa/Padova metabolic simulator (Kovatchev et al. 2009) is used for prediction validation. The academic version of the FDA-approved Type 1 diabetic simulator has 30 in silico subjects (10 children, 10 adolescents and 10 adults). Each subject completed 10 scenarios, each lasting 3 days, based on closed-loop control with a general predictive controller (Turksoy et al. 2014). Then, the CGM dataset of the subjects is used to assess the accuracy of the designed hybrid predictor. For both the training and testing datasets, CGM signals without any preprocessing are used for prediction of glucose concentration values. The sampling interval is 5 minutes and the initial parameters for each candidate filters are specified (Table 4).

Table 4. Parameters for the four algorithms.

Model	Regularization Factor λ	Forgetting Factor β	α for A = αI	q for q = q1/q2
RLS	0.001	0.99	-	-
EX-RLS	0.001	0.99	1	0.01
KRLS	0.001	0.99	-	-
EX-KRLS	0.001	0.99	1	0.01

2.3.2 Clinical Subjects

Clinical experiment data from both open- and closed-loop protocols involving subjects with T1D are used to assess the performance of the proposed approach. For the closed-loop clinical experiments, the subjects, aged 18–35 years, were recruited from the University of Chicago Medical Center, Kovler Diabetes Center and were scheduled for a visit at the University of Chicago General Clinical Research Center. The experiments were approximately 60-hours long and the subjects' own insulin type and pump were used during the experiments (Turksoy et al. 2014). The Guardian REAL-time CGM was utilized to collect the subjects' BGC information every 5 minutes. The open-loop experiments were performed at the University of Illinois-Chicago, College of Nursing (UIC-CON). The subjects used continuous subcutaneous insulin infusion pump therapy for their glucose regulation based on their own meal bolus and correction insulin calculation methods prescribed by their own diabetes care provider. The subjects met with the investigators at the UIC-CON for a total of 3 days; however, some subjects opted split day(s) into 4-hour blocks of time totaling 24 hours. Based on some subjects' schedule, some of the experiments took 2 weeks to 8 weeks (total hours stay at UIC-CON is still the same). The closed-loop experiments involved the artificial pancreas system to automatically compute the required amount of insulin bolus for maintaining the CGM measurements close to the desired target. The open-loop experiments involved subjects regulating their own blood glucose concentration through monitoring their CGM sensor readings and making insulin dosing decisions as they normally would make. Research ethics approvals were obtained and the experimental protocols were certified by the respective institutional review boards (IRB) of the organizations involved. Overall, there are 9 clinical experiments used to evaluate the hybrid predictor, and Table 5 shows the characteristics of the participants of the clinical studies. Based on these clinical experiments, three cases are considered to evaluate the accuracy of the designed hybrid predictor.

Table 5. Demographic information of the nine clinical subjects (six open-loop and three closed-loop).

Demographic criteria	Mean ± standard deviation
Age (years)	24.43 ± 6.24
Body weight (kg)	72.21 ± 16.77
Height (cm)	166.96 ± 9.62
Body mass index (kgm-2)	25.97 ± 5.87
Duration of time with diabetes (years)	14.71 ± 8.91
Waist (cm)	84.75 ± 12.77

The closed-loop clinical subjects are used to evaluate the hybrid predictor in two different ways. The first approach, called Case 1, uses three-day closed-loop CGM data (approximately 56 hours or 670 samples) from each subject to identify the hybrid and regular models and compare their respective predictive performances. The first 70 samples are used to train the models, and subsequently provide predictions for the 30-minutes-ahead glucose outputs online using CGM data up to 200 samples. The prediction results are compared against measurements from CGM and illustrated in Figure 4(a). The second approach, called Case 2, uses a model trained using data from one subject while evaluating the model for on-line predictions in another randomly selected subject. The subject used for collecting training data to develop the model and the subject used to test the model are both selected at random. Such a cross-trained scenario demonstrates the need for personalized models that perform better than the models trained on another subject's data. In this scenario, 200-samples of closed-loop CGM data from a subject denoted A are chosen as training dataset, while the proposed hybrid model is tested using the online measurements of subject B to assess model prediction accuracy. In this way, the ability of prediction could be analyzed at the start point of modeling and the generalization performance of the hybrid model could be presented as well. All the closed-loop experiments considered are randomly divided into either Case 1 or 2, while the open-loop experiments constitute Case 3.

Figure 4.

Comparison of measurements and 30-min predicted glucose profiles for subjects (A1, B1 and C1) in clinical experiments based on hybrid predictor. Subplot (c) plots the first 600 samples and subplot (d) the complete 2000 samples from subject C1 for easy comparison of trends. Associated PRED-EGA analysis shown in Figure 5 and summary statistics provided in Table 8.

With regards to the open-loop data, Case 3 employs 10-day open-loop CGM data (about 3000 samples with 5-min sampling interval) from subjects to evaluate the long-term performance of the proposed predictor. As the open-loop data showed, the glucose concentration values are not well regulated, with the CGM of the subjects in this case, denoted by the identifier tag C, often exceeding the target range (70-180 mg/dl) and potentially leading to hypo- and hyperglycemia complications. Further, subjects in this group were allowed to recalibrate the CGM at their own preference, which caused rapid changes to the regular glucose dynamics. This presents a serious obstacle to the accurate online prediction of glucose values.

2.4 Evaluation Criteria

To characterize the accuracy of glucose concentration prediction compared with actual CGM values, the following metrics are used:

1. Mean absolute relative deviation [MARD (%)] (Noujaim et al. 2007)

   $$\text{MARD}=\frac{1}{N}\sum _{i\in N}\left|\frac{y(i)-\widehat{y}(i)}{y(i)}\right|\times 100\%$$ (8)

   where ŷ(i) is the predicted value, y(i) is the measurement, and N is the number of samples. This metric indicates how closely the prediction results and measurement results match.

2. Root-mean-square error [RMSE (mg/dL)] (Gani et al. 2010)

   $$\text{RMSE}=\sqrt{\frac{1}{N}\sum _{i\in N}{(y(i)-\widehat{y}(i))}^2}$$ (9)

   RMSE has similar units as the predicted variable, making analysis of prediction performance easier.

3. Prediction-error grid analysis (PRED-EGA) (Kovatchev et al. 2004, Sivananthan et al. 2011) PRED-EGA is a new version of the continuous glucose-error grid analysis (CG-EGA) (Clarke et al. 1987). This metric is a reliable and robust approach to evaluate the prediction accuracy of CGM systems because it measures accuracy on both BGC and direction of BGC fluctuations. For evaluating the predictor's accuracy, the point-error grid analysis (P-EGA) is used to describe the correct predictions of BGC. For assessing the predictor's tracking performance, the rate-error grid analysis (R-EGA) is utilized to present the ability to accurately capture the direction of BGC fluctuations.

3. Results

All the prediction methods mentioned above were programmed in MATLAB R2012a for online training and short-term (30-minutes-ahead or equivalently 6 sampling instances ahead) glucose concentration prediction. The dataset containing the hybrid model inputs and desired glucose response are used for updating the model and online prediction. The desired response of a certain prediction horizon (PH) is unknown in real-time, but the current measurement can be used as a desired target for the sample obtained at the t–PH sampling instance to update the parameters of the prediction models.

A. In Silico Subjects

The recursive filters and the proposed hybrid filtering algorithm are applied for on-line glucose prediction using the 30 in silico subjects (10 for each of adults, adolescents, and children). The average errors observed across all the in silico subjects for each category (adults, adolescents, and children) are reported in Table 6. It is readily observed that the performance of the proposed hybrid filtering algorithm is superior to the other filtering algorithms considered in this work.

Table 6. Glucose prediction accuracy for 30 in silico subjects (average results of RMSE, Median, and COD for 10 adults, 10 adolescents and 10 children).

Subject Category	Model	MEAN ±STANDARD DEVIATION	MEDIAN±MAD	COD
Adult	RLS	10.4798+/-8.6218	8.7184+/-6.8603	0.7409
	EX-RLS	11.6128+/-9.6402	9.4767+/-8.34	0.6653
	KRLS	11.2607+/-9.0504	9.5461+/-7.9239	0.7097
	EX-KRLS	10.9972+/-8.9339	8.8897+/-7.4717	0.7056
	Hybrid Model	9.8618+/-8.1756	7.9837+/-6.352	0.7811
Adolescent	RLS	10.6663+/-8.8758	8.2589+/-7.4142	0.7484
	EX-RLS	11.9492+/-9.8108	9.4063+/-8.4958	0.6498
	KRLS	10.7712+/-8.8494	8.3097+/-7.4097	0.7257
	EX-KRLS	11.4954+/-9.2759	9.0602+/-7.4663	0.7005
	Hybrid Model	10.2443+/-8.3716	7.6631+/-6.4068	0.7804
Child	RLS	11.1526+/-9.4226	8.9929+/-7.8486	0.722
	EX-RLS	12.5995+/-10.6147	9.6729+/-8.2804	0.6923
	KRLS	11.1498+/-9.5053	8.6996+/-7.7384	0.749
	EX-KRLS	12.3321+/-10.137	9.6123+/-7.9072	0.6948
	Hybrid Model	10.6077+/-9.104	7.9573+/-6.8943	0.7941

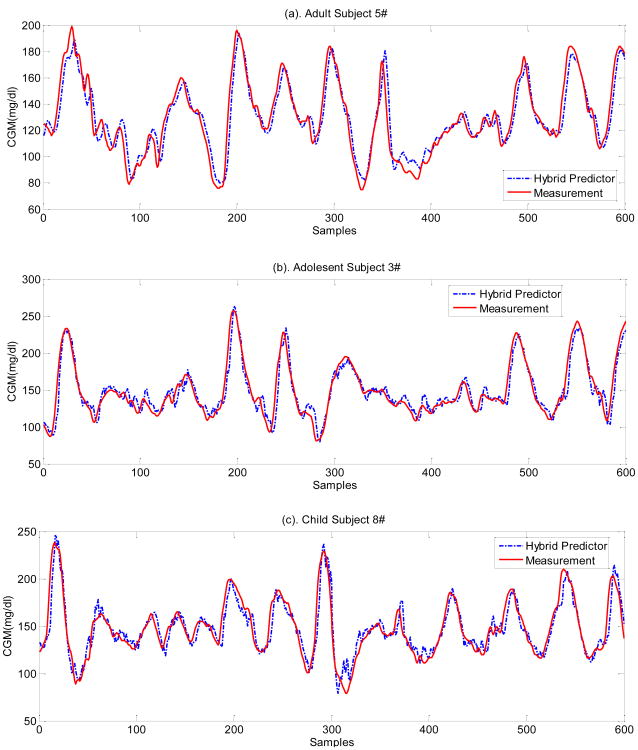
The 30-min-ahead glucose predictions from three randomly selected in silico subjects (adult #5, adolescent #3 and child #8) are shown in Figure 2, with the corresponding PRED-EGA analysis in Figure 3 and the summary statistics tabulated in Table 7. The prediction results of the hybrid model for selected in silico subjects (Figure 2) indicate that the fitted prediction model is accurate and the glucose trends are well captured. For further evaluating the predictor's accuracy in a clinically acceptable metric, the PRED-EGA metric is utilized in terms of both accurate BGC values (P-EGA) and accurate rate and direction of BGC fluctuations (R-EGA) (Kovatchev et al. 2004). Glucose prediction accuracy for in silico subjects is shown in Table 7.

Figure 2.

Comparison of representative measured and 30-min predicted glucose concentration profiles for Subjects #5 (top), #3 (middle) and #8 (bottom) based on hybrid predictor. Associated PRED-EGA analysis shown in Figure 3 and summary statistics provided in Table 7.

Figure 3.

PRED-EGA for adult subjects #5 (a), adolescent subject #3 (b) and child subject #8 (c) based on hybrid predictor. P-EGA compares the predicted CGM to the actual measured CGM. R-EGA compares the rate of change of the predicted CGM (Estimated Rate) to the actual rate of change of the measured CGM (Reference Rate). Associated glucose prediction profiles shown in Figure 2 and summary statistics provided in Table 7.

Table 7. Glucose prediction accuracy for in silico subjects (Adult 5#, Adolescent 3# and Child 8#).

Subject No.	Model	MARD (%)	MEAN ±STANDARD DEVIATION	BG ≤ 70mg/dl			BG 70–180mg/dl			BG ≥ 180mg/dl
				Accurate (%)	Benign (%)	Error (%)	Accurate (%)	Benign (%)	Error (%)	Accurate (%)	Benign (%)	Error (%)
Adult 5#	RLS	6.051	7.935+/-6.875	-	-	-	96.81	2.30	0.88	97.22	2.78	0
	EX-RLS	8.977	10.389+/-8.166	-	-	-	95.74	3.19	1.06	96.67	8.33	0
	KRLS	8.344	11.132+/-9.021	-	-	-	95.74	3.72	0.53	100	0	0
	EX-KRLS	6.323	7.644+/-6.469	-	-	-	96.28	3.55	0.18	100	0	0
	Hybrid Model	5.994	7.538+/-6.514	-	-	-	96.99	2.30	0.71	100	0	0
Adolescent 3#	RLS	7.096	10.748+/-9.585	-	-	-	93.37	5.59	1.04	94.87	3.42	1.71
	EX-RLS	5.830	8.369+/-7.561	-	-	-	94.20	4.35	1.45	97.44	2.56	0
	KRLS	6.145	8.902+/-8.244	-	-	-	93.58	5.38	1.04	95.73	4.27	0
	EX-KRLS	6.653	9.146+/-9.066	-	-	-	93.58	5.38	1.04	95.73	0.85	1.71
	Hybrid Model	5.876	8.221+/-7.593	-	-	-	94.20	4.55	1.24	97.44	2.56	0
Child 8#	RLS	7.591	8.134+/-7.982	-	-	-	93.02	5.62	1.36	94.05	3.57	2.38
	EX-RLS	6.551	7.594+/-7.500	-	-	-	93.02	6.20	0.78	90.48	4.76	4.76
	KRLS	8.979	11.360+/-11.147	-	-	-	93.22	5.62	1.16	95.24	3.57	1.19
	EX-KRLS	7.712	10.967+/-11.185	-	-	-	93.99	4.84	1.16	95.24	3.57	1.19
	Hybrid Model	6.598	7.596+/-7.447	-	-	-	93.41	5.43	1.16	96.43	2.38	1.19

Table 7 summarizes the 30-minutes-ahead prediction accuracy for the hybrid method compared with the four individual candidate filters for three in silico subjects in different groups. The metrics (MARD, RMSE and PRED-EGA) are used to assess their prediction performance. Prediction errors given by MARD and RMSE are presented in the third and fourth columns respectively, and prediction assessments measured by PRED-EGA are given in the last nine columns of Table 7.

In Table 7, predictions are classified as accurate if the predictions fall within the A or B zones of both the P-EGA and the R-EGA. The benign errors refer to predictions with acceptable point accuracy (A or B zones in P-EGA) yet with more significant errors in the rate accuracy (C, D, or E zones in R-EGA). The benign errors are unlikely to lead to negative clinical consequences as the blood glucose predictions are relatively close to the measured values with only the derivative or rate of change of the blood glucose values not predicted accurately. The erroneous predictions (C, D, or E zones of the P-EGA regardless of the corresponding R-EGA zone), labeled under the error heading in Table 7, refers to the samples that have significant prediction errors in the nominal blood glucose values, which could potentially lead to negative clinical actions and outcomes (Kovatchev et al. 2004).

As the glucose of in silico subjects is well controlled (Turksoy et al. 2014), the hypoglycemia is avoided completely. Based on these results, one can observe differences between various prediction models. In general, the proposed hybrid model has higher prediction accuracy than its candidate models in most situations, since it is developed by the model fusion mechanism. This is readily observed in Table 7, where the proposed method has most of the predictions as highly accurate, with only a few samples with benign errors that would not have significant consequences in clinical results. Furthermore, the proposed approach results in lower erroneous predictions that would have negative clinical outcomes, thus improving the overall results compared to the other individual models. It should be noted that it is unrealistic to expect a prediction model that always performs better than others in all three metrics. Table 7 also shows that none of the candidate models could provide as good of a prediction ability at all times and across all subjects as the hybrid model because glucose concentration dynamics often combine different characteristics that require different adaptive models to cover various conditions. Although in a few occasions a candidate model did perform slightly better than the hybrid predictor, this occurred rarely and the hybrid model still performed comparably to the best model in terms of predictive performance. The consistently improved prediction ability of the hybrid model can be attributed to the better characterization of the glucose trajectories. For example, model parameters may be able to fit the data when glucose is increasing, but unable to capture the response fluctuations when glucose declines. Moreover, a specific model may give responses with varying degrees of accuracy to the different subjects. In contrast, the hybrid method provides better prediction and tracking ability, which may result from the fact that the hybrid predictor is developed by online updating based on the fusion mechanism that may overcome the problem of excessive reliance on each candidate model.

B. Clinical Subjects

The glucose predictions from selected clinical subjects are shown in Figure 4, with the corresponding PRED-EGA analysis in Figure 5 and the summary statistics tabulated in Table 8. The hybrid predictor is evaluated using three subjects in each case (subjects A1-3 for case 1, subjects B1-3 for case 2, and subjects C1-3 for case 3). For the sake of brevity, only one set of prediction results is shown in the figures for each of the three cases to demonstrate the efficiency of the modeling approach. The 30-min prediction results for clinical subject A1 (Figure 4) indicate good prediction ability with an acceptable delay, a small RMSE (8.9325 mg/dL) and good accuracy in the PRED-EGA. For the cross-trained model for subject B1, the prediction accuracy is decreased because of subject-depended training data. It presents considerable phase shifts, a larger RMSE of 11.189 mg/dL and a lower accuracy of PRED-EGA. The results for case 2 demonstrate that if training data from another subject is used, the models will always be of lower accuracy as the model dynamics are not in agreement with the test subject. In certain cases, the models identified and used on different subjects may perform reasonably well, though this is only expected in rare cases where the training data involved are similar to the subject's glucose dynamics. For subject C1, the first 600-point comparison of measurement and prediction results is shown in Figure 4(c), and the full 2000-point comparison was shown in Figure 4(d). Figure 4(c) illustrates that the fitted prediction model is accurate even for open-loop glucose prediction and the glucose trends containing more uncertain dynamics are well captured. The detailed analysis with the three metrics shows that the prediction performance of hybrid model is still acceptable and reliable even in such a complex case.

Figure 5.

PRED-EGA for a select number of subjects (A1, B1 and C1) in clinical experiments based on hybrid predictor. P-EGA compares the predicted CGM to the actual measured CGM. R-EGA compares the rate of change of the predicted CGM (Estimated Rate) to the actual rate of change of the measured CGM (Reference Rate). Associated glucose prediction profiles shown in Figure 4 and summary statistics provided in Table 8.

Table 8. Glucose prediction accuracy for clinical subjects (A1, B1 and C1).

Subject No.	Model	MARD (%)	MEAN ±STANDARD DEVIATION	BG ≤ 70mg/dl			BG 70–180mg/dl			BG ≥ 180mg/dl
				Accurate (%)	Benign (%)	Error (%)	Accurate (%)	Benign (%)	Error (%)	Accurate (%)	Benign (%)	Error (%)
Subject A1	RLS	8.141	9.112+/-7.635	97.40	1.30	1.30	96.83	2.54	0.63	94.12	5.88	0
	EX-RLS	7.995	9.188+/-7.543	97.40	1.30	1.30	95.98	3.38	0.63	94.12	5.88	0
	KRLS	9.644	11.164+/-9.397	90.91	0	9.09	97.25	1.90	0.84	94.12	5.88	0
	EX-KRLS	9.741	11.235+/-9.799	93.51	0	6.49	98.31	1.06	0.63	95.59	4.41	0
	Hybrid Model	7.846	8.933+/-7.814	97.40	1.30	1.30	96.83	2.54	0.63	95.59	4.41	0
Subject B1	RLS	10.602	12.967+/-11.606	66.67	0	33.33	85.16	12.26	2.58	93.71	3.14	3.14
	EX-RLS	8.945	10.582+/-11.063	77.78	0	22.22	85.16	12.26	2.58	92.46	4.40	3.14
	KRLS	11.687	13.28+/-11.694	55.56	0	44.44	75.48	21.29	3.23	91.82	3.77	4.40
	EX-KRLS	10.17	12.516+/-11.815	55.56	0	44.44	77.42	20	2.58	93.71	2.52	3.77
	Hybrid Model	9.559	11.189+/-10.987	77.78	0	22.22	82.58	14.84	2.58	93.08	2.52	4.40
Subject C1	RLS	12.284	17.676+/-16.252	93.48	0.43	6.09	92.40	4.75	2.85	77.78	14.81	7.41
	EX-RLS	13.692	23.762+/-29.683	89.57	1.30	9.13	90.74	6.41	2.85	68.52	24.07	7.41
	KRLS	12.695	15.684+/-26.452	94.78	0.87	4.35	93.82	4.04	2.14	77.78	11.11	11.11
	EX-KRLS	13.518	17.149+/-28.393	90.87	1.74	7.39	92.39	4.51	3.09	75.93	11.11	12.96
	Hybrid Model	11.862	15.004+/-18.730	94.35	0.87	4.78	94.06	3.80	2.14	79.63	12.96	7.41

Figure 5 shows the PRED-EGA with the 30-min prediction results for these three clinical experiments (subjects A1, B1, and C1). The performance evaluation (Table 8) shows the model prediction accuracy of a hybrid method compared with four candidate methods for three groups of clinical subjects with predictor outputs. According to the results, the proposed hybrid model has better prediction accuracy in real test environment based on the online adjustment. For subject A1, at the beginning of the online prediction, the accuracy of the hybrid predictor is not adequate because the training data for updating the model is insufficient. As training data accumulates and more data become available for updating the model, the prediction performance improves and the glucose trends are well captured. According to PRED-EGA, 95.59% to 97.40% of the results fall in the clinically-accurate level on full range of BG values. For subject B1, as prediction models are trained by data from another subject, the beginning portion of the online prediction has large errors and delay, which reduces the accuracy rate of the samples in the hypoglycemia range as shown in PRED-EGA. However, the predictions are relatively accurate for hyperglycemia with 93.08% of the samples in the hyperglycemia range accurately predicted to be in that range, for 30-min ahead predictions. For subject C1, as open-loop CGM data are used and the glucose measurements are often out of the target range, compounded with the adverse effects of frequent calibration, the MARD and RMSE are higher than other cases. However, according the PRED-EGA results, the hybrid model still has the 94.35% and 94.06% clinically-accurate glucose predictions in hypoglycemia and euglycemia ranges, respectively. While the number of samples accurately predicted to be within the hyperglycemia range decreases for the 30-minutes-ahead prediction, the predictive accuracy for various prediction horizons is still in a reasonable range.

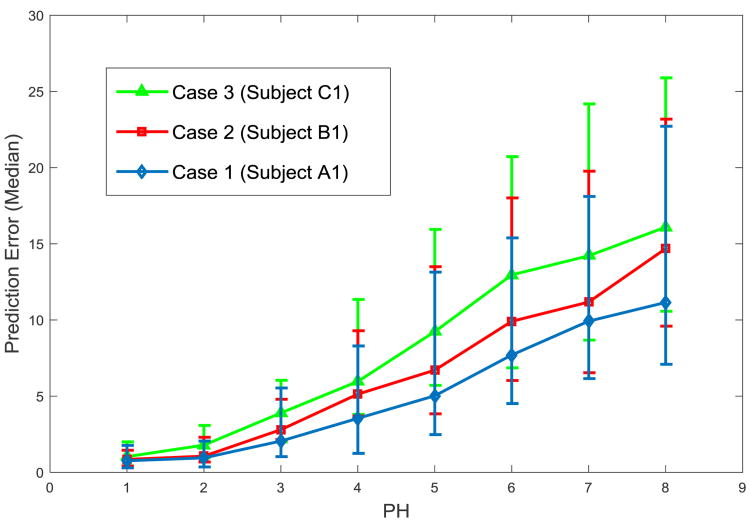
The impact of the prediction horizon (PH) on prediction accuracy is evaluated by comparing the hybrid method in different cases. The median value and the first and third quartiles of the RMSE metric are presented as an error bar. As shown in Figure 6, PH for online prediction is set from 1 to 8 (the prediction period is 5-min to 40-min) and other parameters of the prediction model are the same as the previous simulation. With increasing the PH, the prediction accuracy decreases for all cases analyzed above. In general, case 1 with data from subject A1 shows better prediction accuracy than other cases, as it has well-regulated glucose than case 3 (subject C1) and more adequate empirical training data than case 2 (subject B1).

Figure 6.

Prediction accuracy assessed with different prediction horizons (PH) by the median and first/third quartile of the RMSE.

4. Discussion

Hybrid prediction algorithms have the benefit of assigning greater weighting to the more accurate candidate models compared to other models with higher predictions errors to improve the overall performance. The proposed approach also recursively updates the model parameters at each sampling instance, which generally translates to an even distribution of computation load to each sampling instance. This recursive nature of the model estimation is advantageous for the artificial pancreas application where CGM measurements are sampled uniformly over time. Despite the computational tractability of recursive least squares algorithms, there may in instances where candidate models are identified that do not have sufficient prediction accuracy to merit the computation involved in recursively updating their parameters. This drawback can be mitigated by removing any candidate models from the pool that consistently underperform. Nevertheless, the computational efficiency element of recursive least squares is a topic of future research studies.

In contrast to the RLS model employed in the artificial pancreas application, the proposed hybrid predictor determines weights to effectively combine multiple predictors in order to provide the best prediction performance. As such, in numerous scenarios of the in silico and clinical experiments the prediction results of the hybrid predictor outperformed that of the candidate models. Therefore, the proposed hybrid predictor can outperform the previous model implemented in the AP system, which has predictive performance similar to the RLS approach. In recent multi-model work, a probabilistic framework approach is proposed to combine three parallel predictors using a soft switcher derived from the Bayesian model averaging technique. Although this work shares notions of combining multiple predictors to form a global predictor, the Bayesian model averaging based work showed the merged prediction has predictive performance that is comparable to the best individual predictor. On the other hand, the proposed hybrid predictor in this work determines weights to combine the two models that best characterize the current glucose trends and that provide the best fitting results for the training data. Consequently, the hybrid predictor has some capacity to avoid overfitting of the past training samples and is thus capable of outperforming even the best candidate model on several instances.

As with other data-driven modeling approaches, the veracity and quantity of training samples is of concern in the proposed hybrid predictor approach. This is readily seen in the open-loop results where the subjects rely on their own physician prescribed insulin dosing strategy, which results in more time spent outside the target glycemic zone. This relatively poorer glycemic control in comparison to the closed-loop study, along with the sensor recalibrations, results in CGM data that span a wider range of data. This necessitates models valid over a wider glycemic range, which deteriorates the predictive performance of the models. Nevertheless, the hybrid predictor performed satisfactorily as it usually performs favorably in comparison to the candidate models. Based on the analysis of data from both the in silico and clinical subjects, challenges such as the impact of noise and shifts in CGM sensor readings need to be addressed in future research.

5. Conclusion

In this paper, a hybrid model is developed for online glucose concentration prediction using the model fusion strategy. Combining four candidate filtering algorithms, a fusion mechanism and appropriate weighting scheme are proposed to make accurate predictions. A new hybrid model is designed and applied for short-term online glucose prediction in people with T1D. The work illustrates that the predictive capability of the proposed hybrid model is better compared to each individual prediction model. Moreover, the hybrid method presents a better online prediction accuracy, which can be indicated as a practical and effective approach especially in cases with limited data.