Gene expression variability and the analysis of large-scale RNA-seq studies with the MDSeq

Abstract

Rapidly decreasing cost of next-generation sequencing has led to the recent availability of large-scale RNA-seq data, that empowers the analysis of gene expression variability, in addition to gene expression means. In this paper, we present the MDSeq, based on the coefficient of dispersion, to provide robust and computationally efficient analysis of both gene expression means and variability on RNA-seq counts. The MDSeq utilizes a novel reparametrization of the negative binomial to provide flexible generalized linear models (GLMs) on both the mean and dispersion. We address challenges of analyzing large-scale RNA-seq data via several new developments to provide a comprehensive toolset that models technical excess zeros, identifies outliers efficiently, and evaluates differential expressions at biologically interesting levels. We evaluated performances of the MDSeq using simulated data when the ground truths are known. Results suggest that the MDSeq often outperforms current methods for the analysis of gene expression mean and variability. Moreover, the MDSeq is applied in two real RNA-seq studies, in which we identified functionally relevant genes and gene pathways. Specifically, the analysis of gene expression variability with the MDSeq on the GTEx human brain tissue data has identified pathways associated with common neurodegenerative disorders when gene expression means were conserved.

INTRODUCTION

The analysis of gene expressions via hybridization-based microarray technologies has enjoyed much success in the last two decades. Genes regulating a myriad of human diseases have been identified in microarray studies, including those for brain tumors (1), breast cancer (2–4), skin tumors (5), and a number of neurological disorders (6–8). Nonetheless, microarray experiments can be limited by the presence of cross-hybridization artifacts (9), intensity variability at low expression levels (10), signal saturation of highly expressed genes (11), and partial assessment of genes restricted to annotated transcripts (12). Utilizing next-generation sequencing (NGS) technologies, RNA sequencing (RNA-seq) has largely improved upon the limitations of microarray technologies and rapidly emerged as the preferred tool for transcriptome analysis (12). Ever decreasing costs of high-throughput sequencing have led to the recent availability of large-scale RNA-seq studies by providing datasets with moderate to large sample sizes. These include the Encyclopedia of DNA Elements (ENCODE) (13), the Genotype-Tissue Expression (GTEx) Project (14), the Genetic European Variation in Health and Disease (GEUVADIS) dataset (15), etc. The analysis of large-scale RNA-seq count data presents both new challenges and opportunities.

Gene expression variability can provide important insights on how genes function in biological processes beyond those acquired from standard analysis of gene expression means. For instance, variability analysis of gene expression levels has identified transcriptional regulators in the development of early human embryos (16). Gene expression variability at aberrant levels can suggest disruptions or dysregulations of biological processes (17,18). Recent studies have associated increased levels of expression variability with Schizophrenia (19) and aggressive chronic lymphocytic leukemia (20). A number of methods for the analysis of gene expression variability has been proposed for applications in microarray studies (21–27). However, as early RNA-seq studies often have only a limited number of samples that cannot be reliably applied to assess statistical variability, the analysis of gene expression variability has, so far, been largely ignored in RNA-seq studies that focused on the analysis of gene expression means (28–35). The availability of large-scale RNA-seq studies presents an unprecedented opportunity to evaluate gene expression variability without the encumbrance of the many limitations of microarray technologies.

The analysis of large-scale RNA-seq count data brings about several new challenges that are vital towards the analysis and interpretation of both gene expression mean and variability. Excess zeros, beyond those realized from biological variations, are often present in a significant proportion of genes in large-scale RNA-seq studies. This is often attributed to technical variations from read failures in low-count samples (36) and has been suggested to contribute to elevated levels of overdispersion in RNA-seq data (37). Furthermore, by evaluating a relatively large number of observations, outlying samples are more likely to be encountered in large-scale studies. As gene expression analysis often seeks to interrogate biologically consistent effects across treatments, it is important to identify and remove outlying observations to achieve robust biological interpretation and reproducibility of results (32,38). Most particularly, procedures for differential gene expression analysis often focus on evaluating the null hypothesis that log fold-changes (FCs) between cases and controls are exactly zero, such that there is no differentiation between cases and controls. However, given moderate to large sample sizes, the null hypothesis is often easily rejected, and this can educe a deluge of statistically significant genes, most of which are differentiated at only very modest levels that are biologically uninteresting (39,40). Effective methods are much needed to overcome these challenges in order to provide robust and biologically meaningful analysis of both gene expression mean and variability in large-scale RNA-seq studies.

In microarray studies, log-transformed intensity levels are often assumed to follow a normal or Gaussian distribution (41), and the analysis of gene expression variability usually involves evaluating the normal variances directly (24–26) or conducting heterogeneity tests under assumptions of continuous and symmetric distributions (21–23,27). Yet, RNA-seq counts are both discrete and asymmetrically distributed, such that the analysis of RNA-seq count data requires a much different approach and interpretation from those of microarray data analysis (42).

The Poisson distribution has been proposed for RNA-seq counts that approximates the binomial probability of independently sampled reads (43,44). Given an expected value of E(Y) = μ, a Poisson random variable Y manifests an intrinsic variance of Var(Y) = μ. The Poisson has been largely accepted as a suitable model for the analysis of technical replicates (45,46). However, in large-scale RNA-seq studies, investigators are typically interested in examining biological replicates at different treatment levels in order to interrogate consistent effects of treatments on gene expressions.

Individual subjects in biological replicates engender additional variability over technical ones. The coefficient of dispersion or variance-to-mean ratio ϕ = Var(Y)/μ is a standard measure of additional variability due to biological variations (26,47,48). It has been found to be advantageous in interpreting variability, free from potential finite-number effects due to varying abundances (49,50). Let Y_ig be the read count at subject i and gene g. We employ the mean-dispersion model in this paper based on the coefficient of dispersion, where E(Y_ig) = μ_ig and Var(Y_ig) = ϕ_igμ_ig. The variance of Y_ig consists of a technical μ_ig and biological ϕ_ig component, where μ_ig represents the intrinsic variability due to independent sampling of reads and is biologically uninteresting whereas ϕ_ig characterizes the additional variability arising from biological variations. Thus, interpreting the dispersion ϕ_ig will be the focus of gene expression variability analysis in large-scale RNA-seq studies. Current procedures for RNA-seq counts often assume the negative binomial with the mean-variance relationship Var(Y_ig) = μ_ig(1 + α_gμ_ig), where α_g is invariant across subjects at each gene (28–30,51). Compared to the negative binomial, the mean-dispersion framework can allow for more direct interpretation of variability due to biological variations, such that a log FC in ϕ_ig can be explicitly attributed towards a log FC in total variance where log [Var(Y_ig)] = log (ϕ_ig) + log (μ_ig). An additional advantage is that biological variabilities ϕ_ig are allowed to vary over both individual genes and subjects, with which the power of large-scale RNA-seq studies can be exploited to incorporate dynamic and complex biological relationships. We will provide a generalized linear model (GLM) framework that can incorporate the effects of both treatments and additional covariates on the mean μ_ig and dispersion ϕ_ig. This allows the proposed model to account for a wide array of studies, for example, when cases and controls exhibit different variabilities and when variabilities of gene counts may be influenced by additional covariates, such as age, gender, or different stages in a biological process. In the analysis of RNA-seq data, the average expression strength at a gene has been observed to influence expression variability, where genes with decreased average counts tend to have increased overall variability (51). The mean-dispersion GLM accounts for potential changes in the baseline variability due to differences in average expression counts at each gene by incorporating a gene-wise intercept term in the GLM on dispersion. The incorporation of a dynamic variance model also allows for robust analysis of gene expression means, in addition to enabling the analysis of gene expression variability. In this paper, we present the MDSeq, an efficient toolset based on the mean-dispersion GLM for the analysis of large-scale RNA-seq studies.

The MDSeq utilizes a novel reparametrization of the negative binomial to allow for robust statistical inference and efficient computations of the mean-dispersion model. It includes several important features to address the needs of large-scale RNA-seq studies. (1) As excess zeros can distort model estimation, it is important to account for technical zero counts in order to achieve robust and biologically interpretable results. The MDSeq includes a zero-inflated GLM model, that demarcates an excess zero state for technical zeros due to sequencing failures (36) and a random state that originates all of the nonzero counts and some biological zeros due to probabilistic realizations of the random mean-dispersion model. We will demonstrate that the incorporation of excess zeros in modeling RNA-seq counts can significantly improve power in differential analysis of both gene expression mean and variability. (2) Investigators are often interested in evaluating a given set of parameters of interest. For example, it is often of interest to perform hypothesis tests on treatment effects but not necessarily on those of additional covariates, even though they may be incorporated in the GLM. Cook's distance has been proposed for outlier detection in RNA-seq data analysis (51,52). However, it measures the influences of all parameters simultaneously, such that an observation may be identified indistinguishably as an outlier regardless of whether it is influential on treatment effects or merely the additional covariates. A novel procedure is provided with the MDSeq that allows computationally efficient detection of outliers that are influential for statistical inference on user-specified sets of parameters of interest, that can comprise any or all of the treatment effects and coefficients on additional covariates. (3) It is often of interest to determine genes with differential FCs beyond a given threshold in order to facilitate post-experimental verification and provide reproducible results at measurable expression levels. A common procedure is to select differentially expressed genes that satisfy both a log FC threshold and a p-value significance level (39,40). However, the procedure is relatively ad hoc and cannot be used to determine whether differentially expressed genes satisfy the log FC threshold with statistical significance. In the MDSeq, we develop statistically rigorous procedures for hypothesis tests of both differential mean and variability of expressions at beyond given threshold levels. The development is quite different from those previously proposed for differential analysis of mean expressions (51,71). We will show that the proposed procedure is powerful while controlling type I errors.

The MDSeq is compared with a myriad of existing tools using extensive simulations for both differential expression mean and variability analyses. Results suggest that our procedures are robust and powerful in a wide spectrum of data scenarios. The MDSeq is further demonstrated on two large-scale datasets from the GTEx project, where we uncovered functionally relevant genes and gene pathways in the human skin and cerebral cortex. Excess zeros, outliers, and the need for hypothesis tests at beyond given threshold levels are illustrated on these two real datasets with the MDSeq in Table 1, Supplementary Table S2, and Table 2, respectively. We implemented the MDSeq in a user-friendly R package, freely available at https://github.com/zjdaye/MDSeq. The software allows parallel processing with multiple threads for efficient computations.

Table 1. Genes exhibiting excess zeros in the GTEx tissue data.

	With excess zeros	Without excess zeros
Brain tissue	5555 (21.4%)	20396 (78.6%)
Skin tissue	3739 (14.3%)	22347 (85.7%)

Numbers and percentages, in parentheses, of genes are shown. Expressions of genes are considered to have excess zeros if significance test for presence of excess zeros has p-value <0.05.

Table 2. Genes significant for differential mean and dispersion under various hypothesis tests.

	Mean only	Variability only	Both mean and dispersion	Total
Cortex versus cerebellum brain tissues
|log2FC| ≠ 0	7711 (29.96%)	377 (1.46%)	11,968 (46.51%)	20,056 (77.94%)
|log2FC| > 1	3945 (15.33%)	385 (1.50%)	3214 (12.49%)	7544 (29.32%)
|log2FC| > 2	1489 (5.79%)	117 (0.45%)	774 (3.01%)	2380 (9.25%)
Sun-exposed versus sun-protected skin tissues
|log2FC| ≠ 0	4740 (18.29%)	1896 (7.32%)	2757 (10.64%)	9393 (36.25%)
|log2FC| > 1	12 (0.05%)	53 (0.20%)	49 (0.19%)	114(0.44%)
|log2FC| > 2	4 (0.02%)	7 (0.03%)	8 (0.03%)	19 (0.07%)

The numbers of genes that are significant decrease with more stringent thresholds. Genes are considered significant at FDR q-value <0.05 and insignificant at FDR q-value ≥0.2. Percentages of significant genes are computed out of 25,909 and 25,734 total genes for analysis of the skin and brain tissue data, respectively.

MATERIALS AND METHODS

Mean-dispersion model

Let Y_ig be the read count for sample i and gene g. The MDSeq utilizes a novel reparameterization of the real-valued negative binomial Y_ig ∼ NB(μ_ig, ϕ_ig) in order to allow gene expression variability to be modeled explicitly based on the coefficient of dispersion. For notational simplicity, we assume a given gene g throughout the ‘Materials and Methods’ section and do not specify its index g in the read count Y_ig.

Consider the real-valued negative binomial or Pólya distribution,

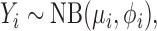(1)

where E(Y_i) = μ_i and Var(Y_i) = ϕ_iμ_i for ϕ_i > 1. The mean-dispersion formulation has the probability model,

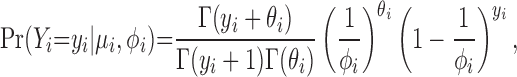(2)

where θ_i = θ(μ_i, ϕ_i) = μ_i/(ϕ_i − 1).

GLM has been applied to extend the classical linear model for RNA-seq counts at the mean expression level (30,34,51,53–55). In this paper, we define the mean-dispersion GLM based on log-linear relationships on both the mean and dispersion, such that

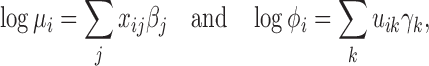(3)

where x_ij and u_ik are design matrix elements and β_j and γ_k are coefficients for the mean and dispersion, respectively. Intercept terms are included on both the mean and dispersion, such that the dispersion intercept allows the MDSeq to account for potential differences in baseline variability due to variations in average expression strengths at each gene (51). The design matrices {x_ij} and {u_ik} include contrasts to indicate treatments on subjects. The MDSeq allows for a number of contrast coding schemes described in Supplementary Methods. For example, in a simple case-control study, one can set x_i1 = u_i1 = 1 for all subjects, x_i2 = u_i2 = 0 for cases, and x_i2 = u_i2 = 1 for controls. Additional covariates describing clinical, demographic, and other experimental factors may also be included in the design matrices {x_ij} and {u_ik}. In many instances, the design matrices {x_ij} and {u_ik} can be the same. However, different contrasts and covariates can be applied in the MDSeq on the mean and dispersion, respectively, to allow applications in a wide array of studies. For example, data sources can be directly incorporated as additional factors in the dispersion GLM, if it is believed that different labs may contribute data at different quality levels and variations.

We used natural logarithms in Equation (3) according to conventions in the GLM literature (56). The natural logarithm and log₂ are related through the identity log₂(·) = log (·)/log (2), and, for convenience, options to output results in the log₂ scale are provided in the MDSeq software. The mean-dispersion GLM can be efficiently estimated via constrained optimization techniques (57,58). Further details are provided in Supplementary Methods.

Modeling excess zero counts

Technical excess zeros are often present in a significant proportion of genes in large-scale RNA-seq data. It is often necessary to incorporate them in order to obtain interpretable results for both gene expression mean and variability analyses. We employ the zero-inflated model (59–62),

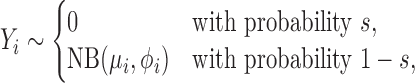(4)

where 0 ≤ s < 1 is the probability of technical excess zeros. Equation (4) describes two states from which RNA-seq counts may arise. An excess zero state is observed with probability s that generates only zero counts, and a negative binomial state is observed with probability 1 − s that generates all of the nonzero counts and a few of the zero counts. That is, the model aims to partition zero counts probabilistically into those arising from technical variations at the excess zero state and those from biological variations at the negative binomial state.

Maximum likelihood (ML) estimates for the zero-inflated mean-dispersion GLM are computed by developing an expectation-maximization (EM) algorithm under constrained optimization (63). Detailed descriptions of algorithm are provided in Supplementary Methods.

Test to determine presence of excess zeros

We evaluate the presence of excess zeros by testing the hypothesis 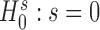against 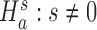in the zero-inflated model of Equation (4). Under the null hypothesis when s = 0, all of the zero counts are assumed to arise from biological variations at the negative binomial state. We apply a likelihood ratio test with the statistic 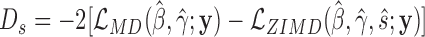, where 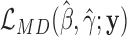and 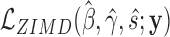are the log-likelihoods at ML estimates of β = (β₀, β₁, …, β_p)^T and γ = (γ₀, γ₁, …, γ_q)^T under hypotheses and 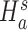, respectively. The log-likelihoods 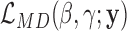and 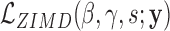are presented in Equations (S2) and (S4), respectively, of Supplementary Methods. Test statistic D_s follows a 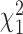distribution under 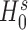, from which we obtain the p-value at the tail distribution. The likelihood ratio test is applied to provide more robust inference, whereas the Wald test has been found to be sometimes unstable for inference on s in zero-inflated models (59,60). When 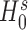is rejected, the zero-inflated model of Equation (4) is applied instead of the usual mean-dispersion GLM (Equation (1–3)) in further analyses.

Wald tests for GLM coefficients

Consider the GLM of Equation (3). We apply Wald tests to evaluate significances of the coefficients β_j and γ_k on log mean and dispersion, respectively, with the statistics 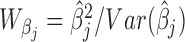and 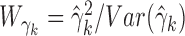, where 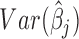and 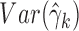are obtained as inverses of observed Fisher informations (64). 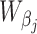and 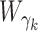follow the 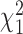distribution under the null hypotheses β_j = 0 and γ_k = 0, respectively, from which we obtain the p-values at the tail distributions. Wald tests for GLM coefficients can be used, for example, in evaluating significances of additional covariates on RNA-seq counts.

The observed Fisher informations for the mean-dispersion and zero-inflated mean-dispersion models are provided in Supplementary Methods, using closed-form Hessian matrices that allow for efficient computations of test statistics.

Standard tests of differential expression mean and dispersion

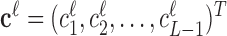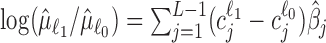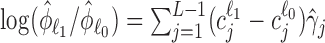Denote as the contrast vector at factor level ℓ. Then, based on Equation (S1) of Supplementary Methods, log FCs of expressions from factor level ℓ₀ to ℓ₁ can be estimated as and for differential mean and dispersion, respectively.

Standard procedures consider hypothesis tests of the alternatives 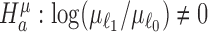for differential expression mean and 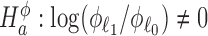for differential dispersion. Wald statistics W_μ for testing 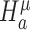and W_ϕ for testing 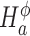are provided in Equation (S9) of Supplementary Methods, with which the p-values are obtained at 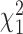tail distributions.

To correct for multiple hypothesis testing across genes, we apply the Benjamini–Yekutieli false discovery rate (FDR) that allows for arbitrary dependence in this paper (65).

Hypothesis tests at beyond a given log fold-change threshold

In large-scale RNA-seq studies with moderate to large numbers of samples, standard tests that evaluate the compliant hypothesis that any change in differential expressions may occur, such as by testing the alternative 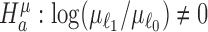, would often result in the selection of a large proportion of genes that are only mildly differentially expressed. To allow for experimental replication and interpretation of results, it is often of interest to identify genes with differential changes beyond a given threshold level. In this paper, we develop rigorous procedures based on one-sided hypothesis tests within restricted parameter spaces (66–68) and union-intersection principle (69,70). The development is quite different from those previously proposed for differential analysis of mean expressions (51,71).

We are interested in evaluating whether the differential mean or dispersion of expressions are significant beyond a given log FC threshold; in other words, we wish to test the alternative hypothesis 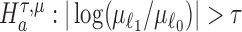or 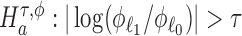, respectively, for some threshold τ > 0. This is accomplished through a two-step procedure. Consider the analysis of differential expression mean. (1) Test of the alternative 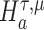is first evaluated asunder as one-sided hypothesis tests of the alternatives 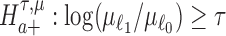and 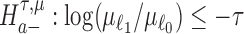. Wald statistics are derived under restricted parameter spaces (66–68), whereas p-values are computed for each test using mixture distributions (72–74). (2) The p-value for testing the composite alternative hypothesis 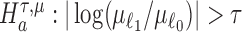is obtained as the minimum of p-values for testing the alternatives 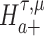and 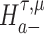by the union-intersection principle (69,70). That is, 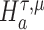is accepted if either of the alternative 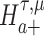or 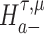is accepted.

Details of thresholded hypothesis tests for differential mean and dispersion are provided in Supplementary Methods. We note that an asymptotically equivalent approach can also be developed based on the likelihood ratio statistics with log likelihoods maximized under restricted parameter spaces (68,74,75). However, this approach requires recomputing GLM estimates under restricted parameter spaces and is computationally more intensive.

Detection of outliers influential for inference on a given set of parameters of interest

RNA-seq data analyses often focus on a set of parameters of interest. For example, in differential expression analysis, one is mainly interested in hypothesis tests involving treatment effects of cases and controls. On the other hand, it is not necessarily of interest to interpret hypothesis tests of additional covariates, although they are often incorporated in the GLM to mitigate conditional effects. In this case, it can be advantageous to focus on the set of parameters of interest, instead of all the parameters as in the Cook's distance (51,52), for efficient detection of outliers.

Suppose that we are interested in evaluating hypotheses based on subsets 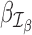and 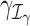of the GLM parameters β = (β₀, β₁, …, β_p)^T and γ = (γ₀, γ₁, …, γ_q)^T, respectively. For instance, in evaluating treatment factors of L levels, the parameters 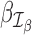and 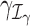are defined as coefficients (β₁, β₂, …, β_{L − 1})^T and (γ₁, γ₂, …, γ_{L − 1})^T, respectively, on the contrast matrix. 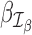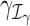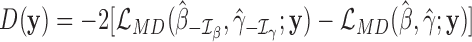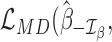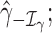A standard likelihood ratio test can be applied for and with the statistic , where 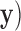is the maximum log-likelihood with the coefficients of 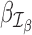and 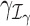set equal to 0. For outlier detection, we do not consider zero-valued counts, as excess zeros are already accounted for by the zero-inflated GLM (Equation (4)).

Traditional procedures for outlier detection are often based on the leave-one-out approach (52,76). Consider the change in the likelihood ratio statistic when sample i is removed, defined as 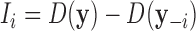where 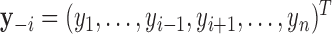is constructed by removing y_i from 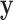and 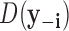is the likelihood ratio statistic computed without sample i. The difference of likelihood ratio statistics I_i provides a natural measure of the influence of the ith sample on inferences based on 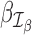and 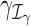, such that an extreme value of I_i may suggest that sample i is an outlier. To identify all the outliers, the influence measure I_i needs to be estimated at each sample i. 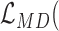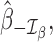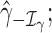However, this involves computing the log-likelihoods 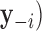and 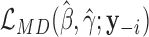repetitively with each sample i removed, which can be computationally prohibitive in large-scale RNA-seq studies.

In this paper, we propose to apply a one-step estimator for I_i based on parameter estimates computed only once on all samples (52,56,77,78). The one-step estimator 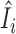is obtained as a weighted sum of standardized deviance and Pearson residuals. Details are provided in Supplementary Methods. We compare 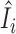to a variance-gamma distribution (79,80) and remove sample i from ensuing analyses if 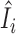is below the (α_out/2)th-quantile or above the (1 − α_out/2)th-quantile of the variance-gamma, where we use α_out = 0.05 in this paper. We note that the estimator 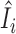is not guaranteed to follow a variance-gamma distribution due to potential estimation error from outliers and dependence. However, we found that the procedure works well in practice, as extreme outliers can be easily identified with the computationally efficient one-step estimator (see Results). The proposed procedure can be applied on any set of parameters of interest, including all parameters.

Data normalization and preprocessing

Normalization is necessary to account for technical biases of read counts at different samples, such as those due to varying sequencing depths. In this paper, we applied the trimmed mean of M values (TMM) procedure, that has been found to be robust against technical biases (30,81). We adjusted the raw counts by using TMM normalization factors provided by the TMM procedure together with the library sizes. Adjusted counts were subtracted by 0.5 and then raised to the smallest integers for the downstream expression analysis. The MDSeq also allows the user to apply other normalization factors, including the relative log expression (RLE) (29), upper-quartile (46), and conditional quantile normalization (cqn) (82) factors. In addition to normalized counts, the MDSeq also provides an option to offset sample-specific normalization factors in the GLM with raw counts. Further details are provided in Supplementary Methods.

RESULTS

MDSeq performs the best for gene expression variability analysis in large-scale studies

We compared the MDSeq with six other methods that have been proposed for variance heterogeneity analysis in microarray gene expression studies. Bartlett's test is a classical procedure for evaluating unequal variances between groups (22,23,83). The Levene's test is a robust alternative to Bartlett's under non-normal data (22,23,27,84–87). It is further improved upon for data with outlying samples by using the trimmed-mean, in which we removed the top 10% outlying samples (88). The heteroscedastic regression, that extends the simple linear regression with nonconstant error variances, has been proposed for detecting genetic loci controlling gene expression variability in microarray studies (24–26,87). We apply the heteroscedastic regression to include additional covariates in this paper; specifically, a normal probability model 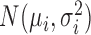is applied where μ_i and 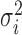are linear and log-linear in treatment factors and additional covariates, respectively. The mean-absolute-deviation (MAD) test has been proposed as a robust procedure for differential variability analysis of microarray gene expressions (21,89). Moreover, the Fligner–Killeen test utilizes a nonparametric approach for variance comparisons (90). Using the R programming language, we applied the Bartlett's test with the bartlett.test function, Levene's tests with leveneTest from the car package, heteroscedastic regression with dglm using the Gaussian family and log-link options, our implementation of the MAD according to Ho et al. 2008 (21), and the Fligner–Killeen test with fligner.test.

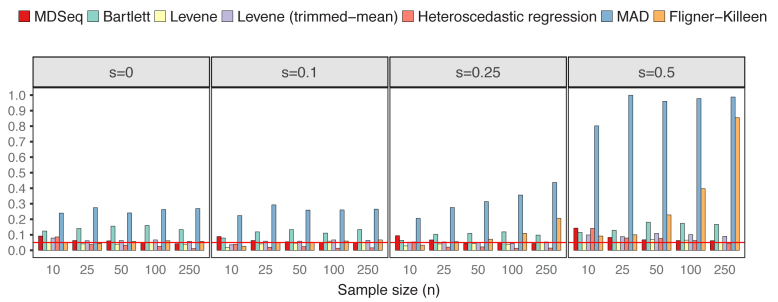
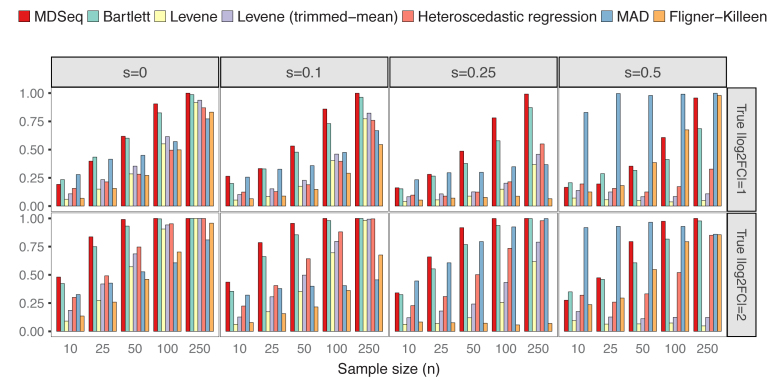
Differential variability analysis is often applied in order to obtain additional insights beyond those already acquired from standard differential analysis of gene expression means. Thus, in this study, we focused on evaluating scenarios when gene expression means are consistent across cases and controls. To compare with Bartlett's, Levene's, MAD, and Fligner–Killeen tests that do not allow the incorporation of additional covariates, we simulated count data from NB(μ₀, ϕ₀) for controls and NB(μ₀, 2^log2FCϕ₀) for cases without additional covariates, where we set μ₀ = exp (5) and ϕ₀ = exp (4) as the constant mean and baseline dispersion, respectively. Excess zeros were incorporated according to the zero-inflated model (see ‘Materials and Methods’ section). Both empirical powers and type I errors for each procedure were estimated as proportions of p-values < 0.05 from 1,000 repetitions, where type I errors were computed under constant variances over cases and controls with log₂FC = 0. Figure 1 presents type I errors at varying probability of excess zeros and sample sizes. The MDSeq, Levene's tests, and heteroscedastic regression have well controlled type I errors at around the theoretical level of 0.05, except when sample sizes are extremely small. On the other hand, both Bartlett's and MAD tests have inflated type I errors in all scenarios with the worst performance at s = 0.5 when the probability of excess zeros is relatively large. This suggests that the Bartlett's test, that tends to be sensitive to departure from normality (84), and the MAD test may be inappropriate for RNA-seq count data, especially when excess zeros are present. The Fligner-Killeen test has well controlled type I errors at s small but can have inflated type I errors at s large, suggesting that excess zeros can effect the nonparametric approach. Figure 2 shows that the MDSeq dominates Levene's tests and heteroscedastic regression in terms of power, when |log₂FC| = 1 and |log₂FC| = 2, in all scenarios, whereas the MDSeq dominates the Fligner-Killeen test except at s large when the Fligner-Killeen test can have inflated type I errors. Further, performances of Levene's tests and heteroscedastic regression, that do not incorporate excess zeros, quickly deteriorate with increasing probability of excess zeros s, whereas the MDSeq remains robust at s large. These results suggest that the MDSeq, based on a zero-inflated GLM count model, can be advantageous for variability analysis of large-scale RNA-seq count data. Scenarios with additional covariates are presented in Supplementary Figures S1 and S2 for type I errors and powers, respectively.

Figure 1.

Type I errors in the absence of differential expression variability. There are n samples of cases and controls each and varying proportions of excess zeros s. The MDSeq, Levene's tests, and heteroscedastic regression have well controlled type I errors for moderate to large sample sizes, whereas Bartlett's and MAD tests have highly inflated type I errors. Results are based on 1,000 simulations without additional covariates. Reference lines (in red) are drawn at the 0.05 error rate.

Figure 2.

Powers of detecting differential expression variability. There are n samples of cases and controls each and varying proportions of excess zeros s and log₂ fold-changes log₂FC. The MDSeq often performs the best when sample sizes are moderate or large. Levene's tests and heteroscedastic regression tend to deteriorate in performance with increasing proportions of excess zeros s. Results are based on 1,000 simulations without additional covariates.

MDSeq is advantageous for mean expression analysis of counts with excess zeros

The MDSeq was compared with six other methods for differential mean analysis. The DESeq2 (29,51) and edgeR (30,34,53–55) are popular procedures for RNA-seq analysis at the mean level. Similar to the MDSeq, these methods were developed based on negative-binomial regressions. We compared with the edgeR using both conditional maximum likelihood (ML) (55) and quasi-likelihood (QL) (31,91) estimates with the robust option (34). The voom from the limma package (33,35) circumvents modeling of count data directly by applying the linear model on log-transformed RNA-seq counts. The tweeDEseq (92,93) applies a general family of Poisson-Tweedie probability models to better account for heavy tails and scenarios when the amount of excess zeros is modest, whereas these properties of RNA-seq counts were modeled directly using a zero-inflated dispersion model in the MDSeq. The ShrinkBayes (37,94) incorporates zero-inflated negative binomial models via a Bayesian framework.

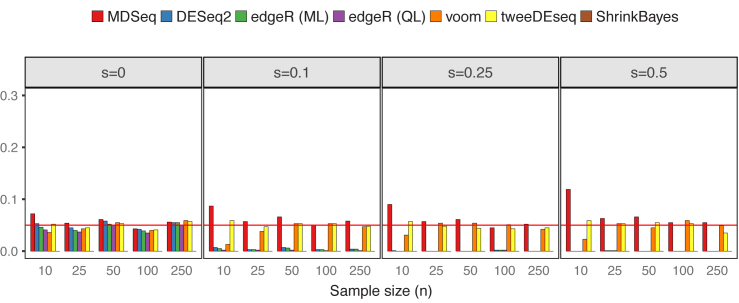
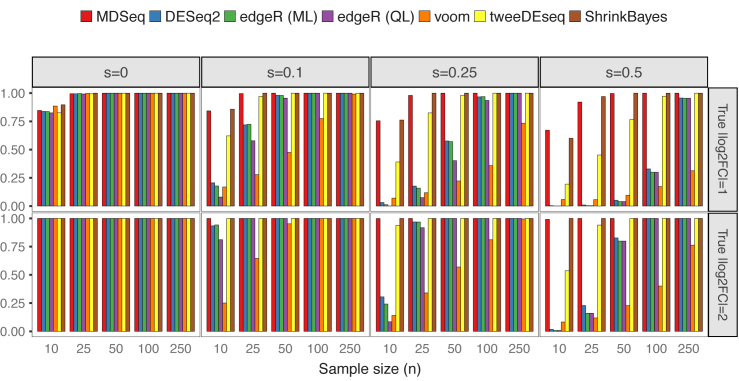
We simulated count data without additional covariates from NB(μ₀, ϕ₀) for controls and NB(2^log2FCμ₀, ϕ₀) for cases, where μ₀ = exp (5) and ϕ₀ = exp (4). Excess zeros were incorporated according to the zero-inflated model (see ‘Materials and Methods’ section). Powers and type I errors were estimated as proportions of p-values < 0.05 from 1,000 repetitions, except that Bayesian false discovery rates (computed with the BFDR function in ShrinkBayes by setting the multcomp option to FALSE) were used for results with the ShrinkBayes (37,94). Figure 3 presents type I errors based on scenarios when gene expression means are consistent across cases and controls. The MDSeq, voom and tweeDEseq generally control type I errors well at around 0.05, while, at extremely small sample sizes, the MDSeq has moderately inflated type I errors. The DESeq2 and edgeR methods control type I errors well at around 0.05 when no excess zeros are present (s = 0), whereas type I errors are nearly 0 when s > 0, suggesting that they may be conservative under the presence of excess zeros. Powers are presented in Figure 4. All methods are comparable in terms of power at s = 0 when no excess zeros are present. However, the performances of DESeq2, edgeR methods, and voom quickly deteriorate under the presence of excess zeros s > 0. This suggests that unaccounted technical zeros may thwart the detection of differential expression means with these methods. The tweeDEseq, that applies a general probability model, performs relatively well under the presence of excess zeros. Nonetheless, the MDSeq and ShrinkBayes, that directly model technical zeros, dominate the tweeDEseq in terms of power when the proportion of excess zeros s is large. This suggests the need to account for technical excess zeros directly using zero-inflated GLMs.

Figure 3.

Type I errors in the absence of differential expression means. There are n samples of cases and controls each and varying proportions of excess zeros s. The MDSeq controls type I errors well at moderate to large sample sizes. DESeq2 and edgeR methods may be conservative under the presence of excess zeros s > 0. Results are based on 1,000 simulations without additional covariates. Reference lines (in red) are drawn at the 0.05 error rate.

Figure 4.

Powers of detecting differential expression means. There are n samples of cases and controls each and varying proportions of excess zeros s and log₂ fold-change log₂FC. The MDSeq and ShrinkBayes often perform the best among methods compared under the presence of excess zeros s > 0. Results are based on 1,000 simulations without additional covariates.

Supplementary Table S1 provides computational times for all methods. The MDSeq can compute for 1,000 simulations in about half a minute or less in all cases. It is faster than tweeDEseq and ShrinkBayes. Although employing a more involved EM algorithm, the MDSeq is faster than DESeq2 at large sample sizes, whereas it is slower than edgeR and voom.

Supplementary Figures S3 and S4 present type I errors and powers, respectively, under scenarios when additional covariates are present. Moreover, Supplementary Figures S5 and S6 present type I errors and powers, respectively, when both expression means and variability are nonconstant across cases and controls. In this scenario, voom has highly inflated type I errors at s = 0 when no excess zeros are present. Further, type I errors increase with increasing sample sizes. This suggests that the voom, although it performs well under equal variances between cases and controls, may be inadequate for RNA-seq count data arising from heterogeneous count distributions. This may be due to the voom relying on a symmetric, normal distributional model (33,35,95) on log-transformed counts, which can be asymmetrically distributed (42). We note that a weighted regression approach may be helpful for mean expression analysis under heteroscedasticity with voomWithQualityWeights (96).

MDSeq provides valid hypothesis tests to evaluate absolute log fold changes above a given threshold

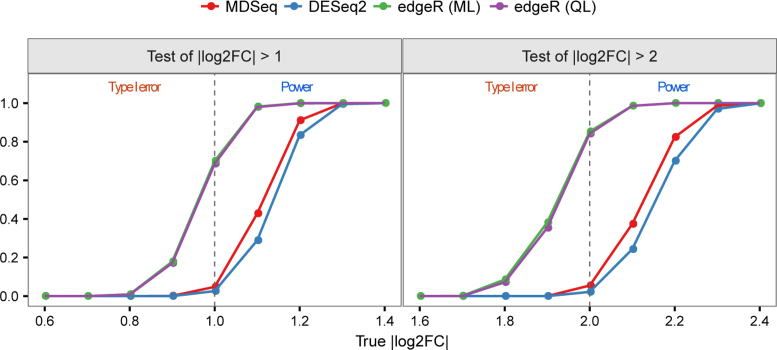
We compared hypothesis tests to evaluate absolute log FCs above given thresholds of expression means for the MDSeq, DESeq2 with the lfcThreshold option, and edgeR using the glmTreat function. The DESeq2 and edgeR do not incorporate technical zeros and were not developed for gene variability analysis. Thus, we did not generate excess zeros and focused on differential expression means in this comparison. In Figure 5, the left panel evaluates the hypothesis H_a: |log₂FC| > 1, whereas the right panel considers H_a: |log₂FC| > 2. We see that the MDSeq controls type I errors well at around or below the 0.05 theoretical level for H_a: |log₂FC| > 1 (H_a: |log₂FC| > 2) when the underlying log FC |log₂FC| ≤ 1 (|log₂FC| ≤ 2). On the other hand, edgeR has inflated type I errors when the underlying absolute log FC is at or moderately less than the given threshold. Moreover, the MDSeq dominates DESeq2 in terms of power when the underlying log FC is above the given threshold. For example, at test of |log₂FC| > 2 when the true |log₂FC| = 2.2, the MDSeq has a power of 0.824 while the DESeq2 has a power of 0.701, that represents an improvement of over 17.5% for the MDSeq. Nonetheless, DESeq2 can be validly applied in most scenarios, as it does not incur inflated type I errors. We note that the MDSeq can further incorporate excess zeros and evaluate hypotheses involving expression variability.

Figure 5.

Hypothesis tests to evaluate absolute log fold-changes of expression means above given thresholds. Type I errors are shown at |log₂FC| less than or equal to a given threshold, and powers are presented when |log₂FC| is greater than the given threshold. The MDSeq and DESeq2 have well controlled type I errors, whereas edgeR methods have highly inflated type I errors when |log₂FC| is at or moderately less than the given thresholds. The MDSeq has greater power than DESeq2 when |log₂FC| is moderately above the given thresholds. There are 500 samples of cases and controls each. Results are based on 1,000 simulations generated from NB(2^log2FCμ₀, ϕ₀) with μ₀ = exp (5) and ϕ₀ = exp (4) for varying log₂FC. No excess zeros were generated with s = 0. Reference lines (in gray) are drawn at the corresponding threshold levels.

Supplementary Figure S7 presents inequality hypothesis tests for differential variability analysis with the MDSeq. Hypothesis tests to evaluate absolute log FCs of expression variability have well controlled type I errors, while powers increase more gradually above the given threshold levels compared with those of hypothesis tests of expression means.

Computationally efficient detection of outliers influential on a set of parameters of interest

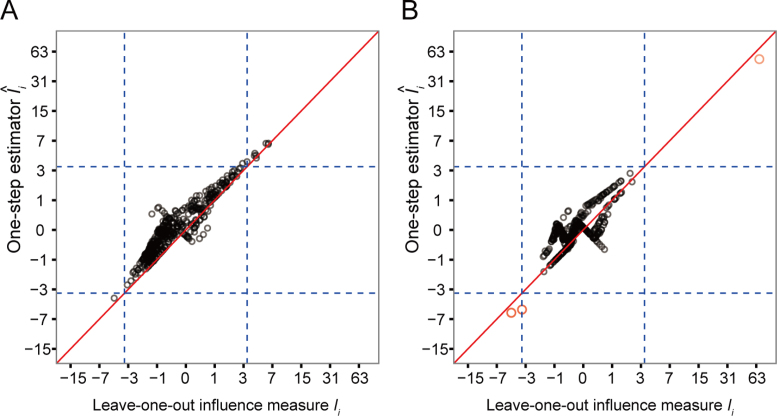
Figure 6 examines the accuracy of the one-step estimator 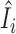versus the leave-one-out influence measure I_i, obtained by repeatedly computing likelihood estimates with each sample i removed. The one-step estimator 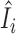closely reflects the true influence measure I_i when no outliers are present (Figure 6A), whereas it is slightly less accurate under the presence of outliers (Figure 6B). We see that inaccuracy due to using a one-step estimation usually does not effect the identification of outliers, which requires influence measures to have fairly large magnitudes at the extreme tails of the variance-gamma distribution. This allows the one-step estimation procedure to provide robust yet computationally efficient outlier detection in large-scale RNA-seq studies. Supplementary Figure S8 illustrates a scenario when there are no outliers influential on treatment effects of cases and controls while observations are indiscriminately identified as outliers when influence on all parameters is considered.

Figure 6.

Accuracy of the computationally efficient one-step estimator 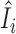. The computationally efficient one-step estimator 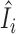is compared with the leave-one-out influence measure I_i under scenarios when (A) there are no outliers and when (B) outliers are present. There are n = 250 samples each for cases and controls. Counts were generated from NB(μ_i, ϕ_i) for controls and NB(2^log2FCμ_i, ϕ_i) for cases with log₂FC = 2, where μ_i = exp (5 + (x_i1 + x_i2)/2) and ϕ_i = exp (4 + (x_i1 + x_i2)/2). Additional covariates x_i1 and x_i2 were simulated from binomial distributions Binom(2, prob = (0.5, 0.5)). In (B), five samples were randomly replaced by outliers simulated from Pois(exp (5)exp (4)). Non-outlying samples (in black) and outliers (in magenta) are plotted. Reference lines (in dashed blue) are drawn at the (α_out/2)th- and (1 − α_out/2)th-quantile of the variance-gamma distribution with α_out = 0.05. A diagonal reference line (in solid red) is drawn at equality of 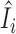and I_i. In (B), all five outliers were identified by the one-step estimator .

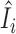Analysis of the GTEx brain and skin tissue data

The Genotype-Tissue Expression (GTEx) project provides an expansive repository of large-scale RNA-seq data across tissue types (97). Recent studies have examined tissue-specific gene expression changes at the mean level using the GTEx data (98,99). However, studies have not been conducted, as far as we know, that effectively examined and accounted for differential changes in gene expression variability across tissue types. In this section, we illustrate applications of the MDSeq on two large-scale RNA-seq studies that compared the expression profiles of brain tissues from the cerebral cortex (obtained from 96 subjects) against those from the cerebellum (103 subjects) and profiles of skin tissues from sun-exposed (302 subjects) against those from sun-protected (196 subjects) epidermises. RNA-seq read counts were obtained from the GTEx Portal (http://www.gtexportal.org, dbGaP Accession: phs000424.v6.p1). Read counts of 26,800 and 26,144 genes with >0.05 average count per million reads across all samples were retained for gene expression analysis in the brain and skin tissue data, respectively. We note that this is a very lenient filtering criterion applied in our data analyses. In practice, a more robust criterion would require a certain number of samples to be above a given count per million reads for both the case and control groups. Further details on data preprocessing strategies are provided in Supplementary Methods. Raw counts were normalized using the trimmed mean of M values (TMM) method (81). Ensuing analyses were performed using the normalized read counts (see ‘Materials and Methods’ section.)

Statistical tests were performed on the brain and skin tissue data to determine if counts of individual genes contain excess zeros (see ‘Materials and Methods’ section). About 21% of individual genes from brain tissues and 14% of genes from skin tissues were found to exhibit significant excess zeros (Table 1). Moreover, estimated proportions of technical zeros can be relatively large for these genes (Supplementary Figure S9). Thus, we see that incorporating excess zeros can be crucial toward the analysis and interpretation of RNA-seq data. Next, outliers were identified at each gene based on the influence statistics 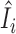with respect to coefficients of contrasts (see ‘Materials and Methods’ section). About 67% of genes from brain tissues and 19% of genes from skin tissues were found to contain at least one outlier at the α_out = 0.05 level (Supplementary Table S2). Samples identified as outliers were removed before further analyses were performed.

Traditional significance tests for H_a: |log₂FC| ≠ 0 and composite hypothesis tests with respect to a given log FC for H_a: |log₂FC| > 1 and H_a: |log₂FC| > 2 were performed. Multiple hypotheses were adjusted using the conservative Benjamini–Yekutieli false discovery rate (FDR) that accounts for arbitrary dependence (65). Due to relatively large sample sizes in these studies, classical tests for no change in expression levels are easily rejected. Hypothesis tests for H_a: |log₂FC| ≠ 0 on the mean and dispersion of RNA-seq counts are significant for about 78% and 36% of genes from the brain and skin tissues, respectively, whereas composite hypothesis tests with respect to a log FC H_a: |log₂FC| > 1 are significant for about 29% and 0.44% of genes from the brain and skin tissues, respectively (Table 2). Volcano plots depicting p-values based on these hypothesis tests are shown in Supplementary Figures S10 and S11 for differential mean and variability, respectively, of the skin tissue data and Supplementary Figures S12 and S13 for differential mean and variability, respectively, of the brain tissue data. Moreover, a number of genes were found to be significant for age and gender covariates (Supplementary Table S3). The MDSeq, based on the GLM, allows for more interpretable results by accounting for potential biological relationships due to additional covariates. Further analyses and interpretation of results are presented as follows.

Differential variability analysis of sun-exposed and sun-protected skin tissues uncovers relevant genes overlooked by mean expression analysis

Table 3 presents genes differentially expressed in the mean or variance. Composite hypothesis tests were performed with respect to at least a two FC in either the mean or dispersion, and the Benjamini–Yekutieli false-discovery rate (FDR) was applied for multiple testing control under arbitrary dependence (65). A myriad of genes in Table 3 that are significant for differential variability but not differential expressions at the mean level are related to sun exposure of skin tissues. For example, studies have shown that ultraviolet radiations can lead to functional irregularities among genes from the histone family (HIST1H1C, HIST1H1E, HIST1H2AE, HIST1H2BG, HIST1H3D, HIST1H3H) (100,101). Keratin is an important structural material in the formation of the epidermis, and disruptions to genes of the keratin family (KRT17P1, KRT39, KRT41P, KRT6B) have been found to cause several skin disorders, including the development of carcinomas (102,103). Moreover, genes of the heat-shock protein family A (HSPA5,HSPA6) have been shown to effect cell responses to ultraviolet irradiation in human skin tissues (104–106). Absolute log FCs tend to be relatively small for these genes at mean expression levels, which may be caused by the fact that sun-exposures on subjects are not severe enough to trigger a significant change in expressions at the mean or that expression means are conserved for these functionally important genes. Results suggest that the analysis of gene expression variability can be a useful addition to traditional differential gene expression analysis at the mean level and can provide an important component towards the interrogation of gene functionality and genetic effects of human disorders. Supplementary Figures S14 and S15 provide p-values from methods at subsets of decreasing sample sizes of the genes found in Table 3, according to an approach from van Wieringen and van de Wiel (107). Full results of significance tests on all genes for both the skin and brain tissues data are provided in Supplementary Data.

Table 3. Genes significant for differential mean and dispersion of sun-exposed versus sun-protected skin tissues with respect to the threshold |log₂FC| > 1.

Gene	Ensembl Gene ID	Differential mean			Differential variability
		log2FC	Statistics	FDR q-value	log2FC	Statistics	FDR q-value
Genes significant for differential mean but not differential dispersion
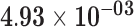
C10orf99	ENSG00000188373.4	1.41	22.61		1.49	7.15	1.00
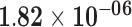
FAM83A	ENSG00000147689.12	−1.66	38.80		−1.56	8.67	1.00
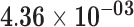
LHFPL3-AS1	ENSG00000226869.2	−1.57	22.88		−1.65	9.18	1.00
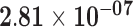
NELL2	ENSG00000184613.6	1.67	42.67		1.30	2.62	1.00
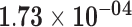
RP11-252C15.1	ENSG00000254813.1	1.52	29.58		1.66	12.82	3.27 × 10−01
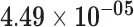
RP11-371I1.2	ENSG00000215808.2	1.69	32.25		1.20	0.79	1.00
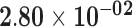
RP11-529A4.7	ENSG00000255305.1	1.56	19.03		1.54	4.13	1.00
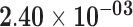
SIX1	ENSG00000126778.7	1.57	24.14		1.33	2.25	1.00
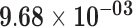
SNORA75	ENSG00000206885.1	−1.43	21.21		−1.06	0.09	1.00
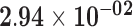
STMN2	ENSG00000104435.9	1.41	18.91		1.65	11.87	5.22 × 10−01
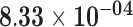
VGLL2	ENSG00000170162.9	1.70	26.33		1.35	2.58	1.00
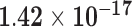
ZNF385B	ENSG00000144331.14	−1.73	90.40		−1.42	5.43	1.00
Genes significant for differential variability but not differential mean
AC003958.2	ENSG00000234859.1	−1.04	0.06	1.00	−2.04	18.98
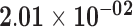
AC018442.1	ENSG00000235683.1	1.26	6.16	1.00	1.96	21.55
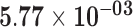
ACKR2	ENSG00000144648.10	1.14	3.46	1.00	1.86	22.98
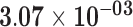
ACTC1	ENSG00000159251.6	1.36	7.82	1.00	1.94	18.50
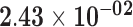
ALOX15B	ENSG00000179593.11	−0.54	0.00	1.00	−1.99	26.32
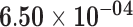
APOC1	ENSG00000130208.5	−1.01	0.00	1.00	−1.78	17.61
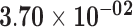
AWAT1	ENSG00000204195.3	−1.78	13.93	3.14 × 10−01	−2.37	23.61
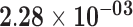
CBLN2	ENSG00000141668.5	−1.76	13.09	4.75 × 10−01	−2.30	22.55
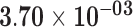
CPHL1P	ENSG00000240216.3	−1.41	5.69	1.00	−2.54	33.46
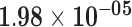
CTB-36O1.7	ENSG00000244921.2	1.24	2.22	1.00	2.87	35.56
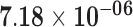
EEF1A1P11	ENSG00000228502.1	0.11	0.00	1.00	1.79	20.11
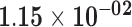
FADS1	ENSG00000149485.12	−0.91	0.00	1.00	−2.06	26.78
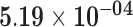
FAR2	ENSG00000064763.6	−0.66	0.00	1.00	−1.86	17.94
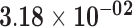
GPRC5D	ENSG00000111291.4	−1.78	10.20	1.00	−2.25	18.97
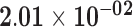
HGD	ENSG00000113924.7	−1.15	1.52	1.00	−2.00	24.81
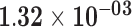
HIST1H1C	ENSG00000187837.2	−0.90	0.00	1.00	−1.92	23.89
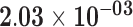
HIST1H1E	ENSG00000168298.4	−1.14	1.36	1.00	−1.85	18.59
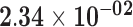
HIST1H2AE	ENSG00000168274.3	−1.15	1.84	1.00	−2.50	58.83
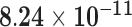
HIST1H2BG	ENSG00000187990.4	−0.99	0.00	1.00	−2.01	26.00
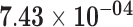
HIST1H3D	ENSG00000197409.6	−1.27	5.81	1.00	−1.96	21.90
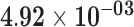
HIST1H3H	ENSG00000203813.4	−1.10	0.71	1.00	−2.09	24.74
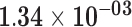
HRK	ENSG00000135116.5	1.43	12.06	7.45 × 10−01	2.27	39.48
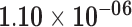
hsa-mir-6723	ENSG00000237973.1	0.57	0.00	1.00	2.09	32.26
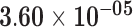
HSD17B2	ENSG00000086696.6	−0.99	0.00	1.00	−1.99	26.22
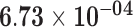
HSPA5	ENSG00000044574.7	−0.74	0.00	1.00	−1.76	18.28
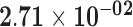
HSPA6	ENSG00000173110.6	−0.91	0.00	1.00	−2.26	42.12
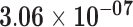
ID1	ENSG00000125968.7	−1.10	0.90	1.00	−1.88	20.41
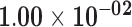
KRT17P1	ENSG00000131885.12	−1.42	6.33	1.00	−2.14	18.97
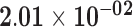
KRT39	ENSG00000196859.3	−1.71	11.89	7.93 × 10−01	−2.12	18.85
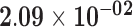
KRT41P	ENSG00000225438.1	−1.75	8.84	1.00	−2.74	22.08
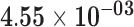
KRT6B	ENSG00000185479.5	−1.19	2.20	1.00	−1.89	20.09
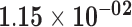
MC5R	ENSG00000176136.4	−1.51	7.97	1.00	−2.29	17.52
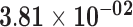
MIR22HG	ENSG00000186594.8	−0.59	0.00	1.00	−1.81	18.87
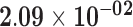
MOGAT2	ENSG00000166391.10	−1.49	12.14	7.22 × 10−01	−2.11	27.50
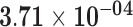
MTND2P28	ENSG00000225630.1	0.42	0.00	1.00	2.09	34.06
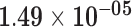
MYH3	ENSG00000109063.10	0.45	0.00	1.00	2.20	46.74
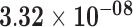
PDE6A	ENSG00000132915.6	−1.67	12.54	6.09 × 10−01	−2.25	22.33
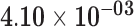
PDZK1	ENSG00000174827.9	−0.93	0.00	1.00	−2.00	26.96
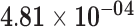
PLIN5	ENSG00000214456.4	−0.95	0.00	1.00	−1.79	17.28
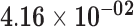
RP11-206M11.7	ENSG00000244468.1	−1.04	0.03	1.00	−2.52	17.45
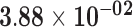
RP11-325K4.3	ENSG00000261270.1	−1.16	2.45	1.00	−1.79	17.33
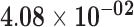
RP11-325P15.2	ENSG00000230832.3	−1.55	5.79	1.00	−2.99	23.82
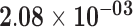
RP11-38H17.1	ENSG00000254366.2	1.37	2.58	1.00	1.92	17.07
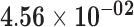
RP11-829H16.3	ENSG00000258525.1	−1.46	12.18	7.22 × 10−01	−2.28	40.13
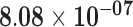
RP11-845M18.6	ENSG00000257829.1	−1.48	3.82	1.00	−2.25	17.59
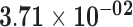
RP11-849I19.1	ENSG00000263146.2	1.04	0.08	1.00	1.74	21.42
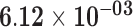
RP4-555D20.2	ENSG00000261786.1	1.21	4.52	1.00	1.85	21.00
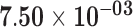
RP5-857K21.7	ENSG00000229344.1	0.71	0.00	1.00	2.66	57.96
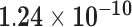
RPL29P14	ENSG00000241112.1	−1.43	12.32	6.77 × 10−01	−2.13	28.36
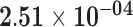
SLC6A1	ENSG00000157103.6	−1.29	12.99	4.96 × 10−01	−1.78	18.75
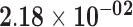
SNORD3A	ENSG00000263934.2	−1.12	0.96	1.00	−1.95	22.95
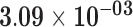
SNORD3D	ENSG00000262202.3	−1.43	7.82	1.00	−2.25	27.69
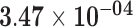
TRIM55	ENSG00000147573.12	−1.63	11.89	7.93 × 10−01	−2.40	25.54

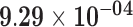
Genes are considered significant at FDR q-value <0.05 and insignificant at FDR q-value ≥0.2. Significant FDR q-values are boldfaced. The log₂ fold-change log₂FC, test statistics, and FDR q-value with respect to the threshold |log₂FC| > 1 are shown. Positive log₂FC indicates over-expression in the sun-exposed skin tissue, and negative log₂FC indicates over-expression in the sun-protected skin tissue.

Gene expression variability reveals functionally important pathways in the cerebral cortex

We examine significances of gene-set pathways in terms of differential mean and variability via gene-set enrichment analysis (GSEA) (108). GSEA is performed with the software GSEA v2.2.0, obtained from http://software.broadinstitute.org/gsea, using default parameters. Genes are ranked using Wald's statistics derived from the null hypothesis H₀: log₂(FC) = 0 for differential mean and dispersion. This allows us to account for lowly expressed or low variance genes with potentially significant FCs in the mean or dispersion, respectively (109). GSEA using all potentially differential genes can provide an important ancillary analysis, that complements gene-by-gene significance analysis with respect to a given threshold level.

Table 4 presents enriched pathways in terms of differential mean or variability for the brain tissue data. Normalized enrichment score (NES) accounts for both differences in gene-set sizes and correlations between gene sets, whereas the FDR q-value is estimated based on the NES and is adjusted for gene-set sizes and dependency (108). Out of 1,003 pathways, two exhibited enrichment in terms of expression means only, six exhibited enrichment in terms of variability only and 90 exhibited enrichment in both mean and dispersion.

Table 4. Significantly enriched pathways for differential mean and dispersion of cortex versus cerebellum brain tissues.

GO term	Ontology	No. genes	Differential mean		Differential variability
			NES	FDR q-value	NES	FDR q-value
Pathways significant for differential mean but not differential dispersion
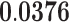
Organelle Localization	BP	23	1.67		1.28	0.207
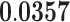
Positive Regulation Of Phosphate Metabolic Process	BP	21	1.68		1.25	0.243
Pathways significant for differential variability but not differential mean
Cell Cell Adhesion	BP	74	1.23	0.275	1.66
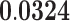
Galactosyltransferase Activity	MF	15	1.15	0.377	1.64
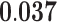
Hemopoietic Or Lymphoid Organ Development	BP	67	1.14	0.405	1.59
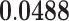
Hemostasis	BP	39	1.30	0.216	1.59
Kinase Regulator Activity	MF	42	1.29	0.222	1.62
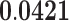
Protein Kinase Regulator Activity	MF	36	1.30	0.216	1.65

Pathways are considered significant at FDR q-value <0.05 and insignificant at FDR q-value ≥0.2. Significant FDR q-values are boldfaced. The normalized enrichment score (NES) and FDR q-value for NES are shown. Positive NES indicates enrichment in the cortex, and negative NES indicates enrichment in the cerebellum.

Pathways enriched for gene expression differential variability often indicates functional differences between the cerebral cortex and the cerebellum. Cell-cell adhesion is foundational in the reorganization and assembly of neural circuits (110). Enrichment of cell-cell adhesion pathway may suggest increased variation and plasticity of the cerebral cortex relative to the cerebellum (111). Galactosyltransferase activity functions to catalyze the transfer of galactose to acceptor molecules. Chronic injection and build-up of D-galactose in mice have been used to model neurodegeneration and brain aging in pharmacological research (112–114). A study has noted that galactosyltransferase activity decreases progressively after birth in the cortex but not the cerebellum in mice, suggesting that galactosyltransferase activity is relatively stable in the cerebellum but variant in the cortex (115).

Moreover, pathways enriched for gene expression variability in the cortex have been found to be associated with common neurodegenerative disorders effecting the cerebral cortex, such as Alzheimer's disease and dementia. Hemopoietic or lymphoid organ development involves the progression of hematopoiesis or hemopoiesis by differentiation. It is an important process in the regeneration of brain tissues. Enrichment of hemopoietic development may indicate increased variation of tissue regenerations in the cerebral cortex relative to the cerebellum. The hematopoietic system has been associated with and proposed as target for treatment of Alzheimer's disease (116,117). Hemostasis involves the avoidance or arrest of bleeding by mediating the circulation of blood. The brain has been known to possess a sophisticated hemostasis regulatory system that protects itself from hemorrhagic injury (118). Enrichment of hemostasis variability may reflect a functional reaction to microbleeding in the cerebral cortex. Studies have found strong correlation between cerebral microbleeding and leukoaraiosis or diseases effecting cerebral white matters (116,119) and Alzheimer's disease (120). Kinase regulator activity and protein kinase regulator activity have been known to play important roles in memory and learning (121). Aberrations in the regulation of kinases have been shown to contribute towards the development of Alzheimer's disease (122–124). Therapeutic strategies targeting protein kinases of the central nervous system have been proposed (125).

On the other hand, pathways significantly enriched in terms of mean expression instead of expression variability are involved in essential biological processes that, due to evolutionary pressure, are rarely observed to contribute to common neurological disorders. Organelle localization involves essential processes of transportation and maintenance of organelles in regions of the cell that are important to normal functions of neurons. Moreover, regulation of phosphate metabolic processes is a primary means of energy regulation. For example, phosphorylation of glucose, the most significant source of energy in the brain, is needed to initiate essential pathways in the usage and storage of glucose.

Pathways significant only for differential mean or differential dispersion for the skin data are provided in Supplementary Table S4. Full GSEA results for both the skin and brain tissues data are available in Supplementary Data.

DISCUSSION

In this paper, we have presented the MDSeq that offers an efficient and comprehensive solution set for the analysis of gene expression means and variability in large-scale RNA-seq studies. The MDSeq utilizes a novel likelihood-based approach to incorporate the mean-dispersion model in a GLM framework. It introduces a zero-inflated GLM to account for technical excess zeros frequently encountered in RNA-seq data. A new approach is developed for detecting outliers influential on a user-specified set of parameters of interest, that is computationally efficient. Further, statistically rigorous hypothesis tests for gene expression differences beyond given threshold levels are provided for both differential analyses of gene expression means and variability, that allow differentially expressed genes to be identified with statistical significance at biologically interesting levels. The MDSeq has been shown with extensive simulation studies to be advantageous for the analysis of gene expression variability on large-scale RNA-seq data and for the analysis of gene expression means of RNA-seq counts with technical excess zeros. The MDSeq has been shown to perform well in the simulation scenarios considered for n ≥ 25. Applications of the MDSeq on the analyses of the GTEx skin and brain tissues data have identified functionally relevant genes and gene pathways. In particular, gene variability analysis of the human brain tissue data has revealed pathways associated with common neurodegenerative disorders, such as Alzheimer's disease and dementia.

The mean-dispersion model applied in the MDSeq is related to the quasi-Poisson, that considers the mean-variance relationship E(Y) = μ and Var(Y) = ϕμ for any positive ϕ > 0 (56,91,126,127). The quasi-Poisson is developed based on the quasi-likelihood in order to avoid the difficulty of building a probability likelihood model for count data when ϕ can assume an arbitrary positive value (91). In this paper, we focused on modeling the mean-variance relationship Var(Y_ig) = ϕ_igμ_ig for over-dispersed data when ϕ > 1. A probability likelihood model is developed using a novel approach based on a reparametrization of the negative binomial (see ‘Materials and Methods’ section). This allows the MDSeq to take advantage of an array of theoretical results and techniques from maximum likelihood theory. For example, the one-step estimator proposed for outlier detection is based on theoretical approximations of probability likelihoods. Moreover, we note that under-dispersion is rarely encountered in RNA-seq studies and can often be attributed to extreme proportions of excess zeros (128). The mean-dispersion model naturally accounts for and qualifies our model for over-dispersion ϕ_ig > 1 using the negative binomial, whereas technical excess zeros are evaluated and demarcated using the zero-inflated GLM. These features allow the proposed model to be robust for the analysis of RNA-seq count data.

The MDSeq variance model Var(Y_ig) = ϕ_igμ_ig is motivated from the coefficient of dispersion ϕ_ig = Var(Y_ig)/μ_ig, that has been found to be advantageous in evaluating additional variability under varying abundances (49,50). Another measure often used in evaluating additional variability is the coefficient of variation 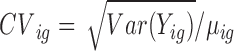or coefficient of variation squared 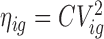(129–131). The MDSeq could potentially be developed based on the mean-variance relationship 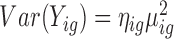motivated from the coefficient of variation. We note that the reparametrization of the negative binomial in the MDSeq can be analogously developed to attain a probability likelihood model for the alternative variance relationship when η_ig > 1. However, investigators are usually interested in the analysis of gene expression variability in order to interrogate additional information beyond those already acquired in the standard analysis of gene expression means. Thus, differential variability analysis is often most informative when mean expression levels are consistent across treatments. In this scenario, as μ_ig is undifferentiated, the analysis of gene expression variability would be unaffected by the choice of the mean-variance relationship.

The MDSeq utilizes a zero-inflated GLM to account for excess zeros in Equation (4). We note that the probabilistic framework is agnostic to the sources of excess zeros. It only requires estimations of the overall probability of excess zeros at a given gene in order to provide robust inference on biological variations at the random negative binomial state. For example, the MDSeq is expected to remain relatively stable when proportions of excess zeros are different across cases and controls but the overall proportions of excess zeros are the same, especially at moderate to large sample sizes (Supplementary Tables S5 and S6).

In this paper, we focused on differential analyses of gene expression means and variability due to the prevalence of case-control data in large-scale RNA-seq studies and their importance towards the identification of functional impacts of genes. The analysis of variance quantitative trait loci (QTLs) that associates genetic variants with quantitative traits has drawn much attention in recent literature (22–26,87,132–135). Variance QTLs can be a source of gene expression variability and play an important role in the genetic regulation of complex traits. The identification of variance QTLs can also help to uncover interactions among genetic variants due to the increased variability of traits influenced by genetic interactions. The MDSeq can be directly applied for the analysis of variance QTLs with RNA-seq data by associating genetic variances with discrete quantitative traits.

Moreover, the MDSeq can be applied for other types of high-throughput count data, such as Chromatin Immunoprecipitation (ChIP) sequencing (136,137), CRISPR/Cas assay (138), etc. Standard RNA-Seq expressions are often profiled by averaging over a large number of individual cells. Recent developments have led to the availability of single-cell RNA sequencing (scRNA-seq) data, that characterize gene expressions at each individual cell (139–142). Gene expression variability analysis of scRNA-seq (143–145) will allow the evaluation and interpretation, at unprecedented resolution, of biological variations among individual cells, that can lead to new insights on cell populations effected by tumor mutations (146,147), infectious diseases (148), etc. In future works, we plan to extend the MDSeq for the analysis of gene expression variability in these studies.

CONCLUSION

The MDSeq is available in an efficient and user-friendly R package at https://github.com/zjdaye/MDSeq. Outlier detection and differential analyses for around 20,000 genes and 200 samples took ∼20 min using four parallel processes on a Windows machine with 3.6-GHz i7-4790 CPUs and 8-GB RAM. With rapidly decreasing cost of NGS, large-scale RNA-seq studies will soon become routinely available. In this paper, we presented the MDSeq to fulfill the need for a comprehensive toolset to interrogate both gene expression means and variability in large-scale RNA-seq studies.

A large number of simulation scenarios has been considered in this article and its accompanying Supplementary Materials. We hope that our results by encompassing a wide spectrum of data scenarios will help to guide practitioners in designing their own experiments. The MDSeq software also contains a sim.ZIMD function that can provide simulated data for type I error and power analysis in additional scenarios.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.