Fig. 2.

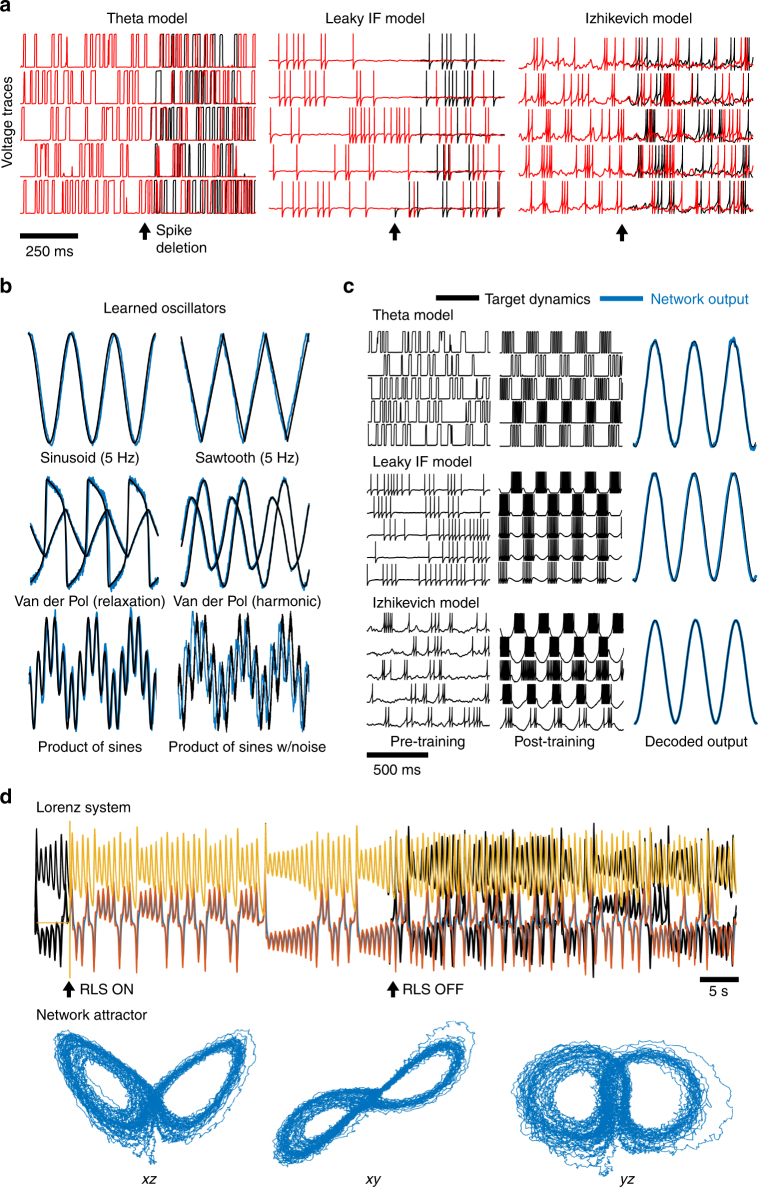
Using spiking neural networks to mimic dynamics with FORCE training. a The voltage trace for 5 randomly selected neurons in networks of 2000 integrate-and-fire spiking neurons. The models under consideration are the theta neuron (left), the leaky integrate-and-fire neuron (middle), and the Izhikevich model with spike frequency adaptation (right). For all networks under consideration, a spike was deleted (black arrow) from one of the neurons. This caused the spike train to diverge post-deletion, a clear indication of chaotic behavior. b A network of 2000 theta neurons (blue) was initialized in the chaotic regime and trained to mimic different oscillators (black) with FORCE training. The oscillators included the sinusoid, Van der Pol in harmonic and relaxation regimes, a non-smooth sawtooth oscillator, the oscillator formed from taking the product of a pair of sinusoids with 4 Hz and 6 Hz frequencies, and the same product of sinusoids with a Gaussian additive white noise distortion with a standard deviation of 0.05. c Three networks of different integrate-and-fire neurons were initialized in the chaotic regime (left), and trained using the FORCE method (center) to mimic a 5 Hz sinusoidal oscillator (right). d A network of 5000 theta neurons was trained with the FORCE method to mimic the Lorenz system. RLS was used to learn the decoders using a 45 s long trajectory of the Lorenz system as a supervisor. RLS was turned off after 50 s with the resulting trajectory and chaotic attractor bearing a strong resemblance to the Lorenz system. The network attractor is shown in three different viewing planes for 50 s post training