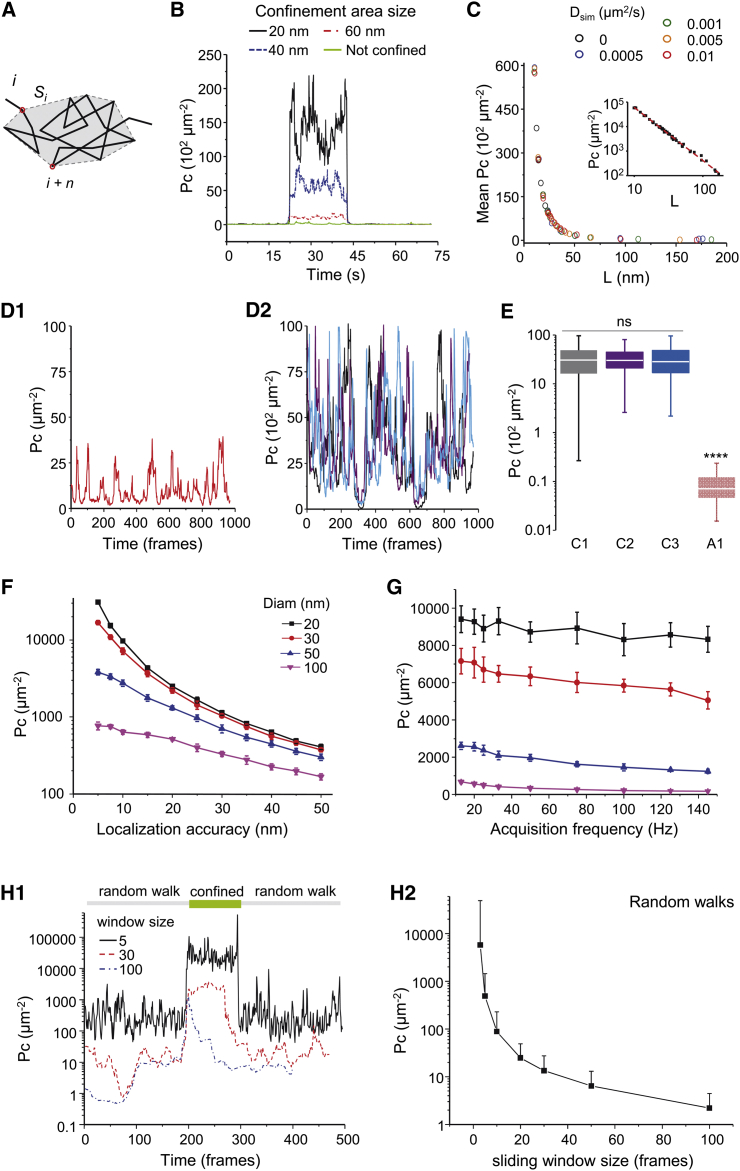
Figure 2.

Detection of transient confinement using the packing coefficient (Pc). (A) A scheme representing the calculation of Pc at time point i. S_i is the convex hull of the trajectory segment i−i+n. The sum of the square displacements between successive time points of the trajectory stretch spanning from i to i+n is divided by S_i². (B) Pc values of examples of 75 s-long simulated trajectories are given that were fully Brownian (green) or that have a period of confinement in areas of the indicated sizes. (C) The mean Pc versus the diameter of the confinement area L on simulated trajectories constructed with the indicated D_sim. (Inset) The same plot in log-log axis (D) Pc values of the simulated trajectories A1 (D1, always Brownian) and C1–C3 (D2, with immobilization periods; C1 in black, C2 in purple, C3 in blue) of Fig. 1. (E) Pc values for the trajectories in (D) (median, 25–75% interquartile range (IQR)), Kruskal–Wallis test with Dunn multiple comparisons; ns, not significant, ^∗∗∗∗p < 0.0001). (F) The mean values of Pc during confinement periods of the indicated sizes, obtained on trajectories simulated with different localization accuracies (mean ± SE, n = 1000; note the semilog scale). (G) Values of Pc are given during confinement periods of the indicated sizes, obtained on trajectories simulated with a localization accuracy of 10 nm and an interval of time between trajectory points that matched the desired acquisition frequencies (see Materials and Methods). (H) The effect of the size of the sliding window. (H1) Pc values of simulated trajectory with a confinement period of 100 time points. Pc was calculated using different sliding window sizes. The largest windows (100 time points) could not detect properly the confinement period. The shortest window (five time points) accurately detected this period, but the fluctuations were significantly higher than for longer sliding windows (note the semilog scale). (H2) Pc values (mean ± SE, n = 1000) were obtained on Brownian simulated trajectories using different sliding window sizes. The statistical uncertainty increases in shorter windows. To see this figure in color, go online.