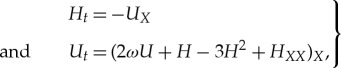Shallow water equations for equatorial tsunami waves

Abstract

We present derivations of shallow water model equations of Korteweg–de Vries and Boussinesq type for equatorial tsunami waves in the f-plane approximation and discuss their applicability.

This article is part of the theme issue ‘Nonlinear water waves’.

1. Introduction

We consider two-dimensional one-layer oceanic flows in the equatorial region. Using methods from asymptotic analysis, we derive two shallow water model equations for waves of small amplitude from the f-plane approximation of the Euler equations for divergence-free incompressible fluids with the usual boundary conditions for free surface waves over a flat bed. In contrast with well-known shallow water models, such as the Korteweg–de Vries equation (KdV), our equations account for the effects of the Earth's rotation on the fluid, the so-called Coriolis effect, which becomes relevant for large-scale ocean waves.

Introducing suitable far-field variables, we derive the following geophysical KdV-type equation (gKdV)

1.1

where η denotes the free surface elevation and ω₀ is a constant related to the Coriolis effect (see §2). We provide explicit travelling wave solutions of gKdV and compare them to the explicit solutions of the standard KdV to analyse the effect of the Coriolis term 2ω₀η_ξ, cf. §3. We proceed with a discussion on the applicability of gKdV for tsunami waves in equatorial regions. Our considerations extend the papers [1–3] to include the Coriolis effect.

Similarly, as for the standard KdV equation, we find that also for gKdV the balance between nonlinear effects and dispersion in the far-field is reached only after extremely large distances. Hence, the applicability of this model is questionable, cf. §4. This suggests the derivation of an alternative model equation in the near-field, where the balance between nonlinearity and dispersion occurs at much shorter, realistic distances. Using near-field variables and the additional assumption of an irrotational velocity field, we derive the following geophysical Boussinesq-type equation (gBouss)

1.2

where H is related to the free surface elevation and ω is a constant related to the Coriolis force (cf. §5). This equation possesses explicit travelling wave solutions for wave speeds greater than the linear propagation speed, cf. remark 5.1. The effect of the presence of the Coriolis term on the shape of the travelling waves is apparent from the explicit expression for the solutions, similarly as for gKdV. In §6, we discuss the applicability of both gKdV and gBouss as models for tsunami wave propagation.

The modelling of ocean dynamics which include the Coriolis effect in different geophysical contexts is of increasing interest. For general qualitative investigations near the Equator including the effects of density stratification and the interaction of waves with depth-dependent currents, we refer the reader to the discussions in [4–13] and the references therein. For an investigation of the effects of underlying currents on the propagation of tsunamis, we refer to [14]. Exact solutions are presented in [15–19]. For a numerical study on the influence of the Coriolis force on the propagation of tsunami waves in the tropical ocean, we refer to [20]. The geophysical models derived in the present paper do not capture such complex interactions. In a first stage of investigation, however, the restriction to two-dimensional flows in the f-plane approximation is reasonable because the Equator acts as a wave guide (see [21]) and the depth-dependent currents are confined to a shallow near-surface layer with considerable attenuation at the free surface (i.e. variations due to internal waves and underlying currents will not affect the surface, see the discussion in [6]). It is worth noting that a two-component rotational Camassa–Holm system modelling equatorial waves was derived in [22]. Furthermore, a geophysical Camassa–Holm equation was derived in [23] for irrotational one-layer equatorial flows by means of variational techniques. Moreover, we point to [24] for a discussion of qualitative aspects of the flow beneath periodic travelling equatorial waves in the f-plane approximation.

2. The governing equations in the f-plane

For the modelling of oceanic wave motion in a neighbourhood of the Equator, it is reasonable to consider the f-plane approximation of the inviscid Euler equations for two-dimensional flows, cf. [25] and the discussion in [6]. Together with the usual boundary conditions for one-layer flows, this system of equations, written in physical variables, is given by

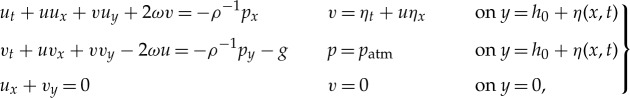2.1

where t denotes the time and x, y denote the directions of increasing azimuth and vertical elevation, respectively. Analogously, u=u(x,y,t) and v=v(x,y,t) denote the horizontal and vertical fluid velocity component in the direction of increasing azimuth and elevation. Moreover, p=p(x,y,t) denotes the pressure and η(x,t) measures the free surface elevation above an average water depth h₀. The constant ω≈7.29×10⁻⁵ rad s⁻¹ denotes the rotational speed of the Earth around the polar axis, thus the two ω-terms in (2.1) capture the effects of the so-called Coriolis force. We denote by p_atm the atmospheric pressure, g≈9.81 m s⁻² is the gravitational acceleration and ρ denotes the constant fluid density.

To non-dimensionalize the set of equations (2.1), we use standard reference length scales: a typical amplitude of the surface wave a, the average undisturbed water depth h₀ as the vertical scale and a typical wavelength λ as the horizontal scale, cf. [2,26,27] for more details. We introduce (without changing the notation) the following set of non-dimensional variables:

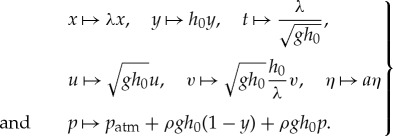2.2

The constant ω related to the Coriolis force is brought to dimensionless form by the scaling

2.3

In view of the non-dimensionalization (2.2) and (2.3), the governing equations read

2.4

where we have introduced the two fundamental dimensionless parameters

2.5

referred to as the amplitude and the shallowness parameter, respectively.

This paper deals with shallow water equations which model tsunami waves in the vicinity of the Equator. In such regions, large parts of the ocean bed are almost flat, as assumed in our model, and located at depths between 2000 m and 4000 m, cf. [28]. Average amplitudes of observed surface waves take values up to several metres, while a typical tsunami wave has an amplitude of approximately 1 m. This implies, in view of the scaling (2.3), that the amplitude parameter ε and the Coriolis parameter ω are of the same order of magnitude: the size of both ε and ω is approximately 10⁻³ m, see table 1.

Table 1.

The non-dimensional parameters ω and ε are of the same order of magnitude for typical values of water depth and wave amplitude for offshore ocean waves near the Equator.

		ε=a/h0
h0		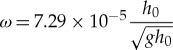a=1 m	a=3 m	a=5 m	a=7 m	a=9 m
1500 m	0.0009	0.0007	0.0020	0.0033	0.0047	0.0060
2000 m	0.0010	0.0010	0.0015	0.0025	0.0035	0.0045
2500 m	0.0012	0.0004	0.0012	0.0020	0.0028	0.0036
3000 m	0.0013	0.0003	0.0010	0.0017	0.0023	0.0030
3500 m	0.0014	0.0003	0.0009	0.0014	0.0020	0.0026
4000 m	0.0015	0.0003	0.0008	0.0013	0.0018	0.0023

It is, therefore, reasonable to assume that

2.6

for some appropriate constant ω₀, see remark 2.1. Additionally, we perform the usual scaling u↦εu, v↦εv, p↦εp, see [2] for more details, to obtain the governing equations for equatorial waves in scaled, dimensionless form:

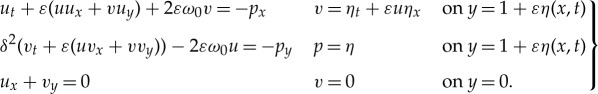2.7

Remark 2.1 —

In view of (2.3), (2.5) and the scaling (2.6), we find that the non-dimensional constant and therefore

2.8

As ω₀ should not alter the order of magnitude in (2.6), we require that 1/2<ω₀<5. Figure 1 shows the range of water depths and wave amplitudes required for assumption (2.6) to be applicable.

Figure 1.

The shaded region indicates for which values of amplitude and water depth the scaling relation (2.6) is applicable; the curves depict the corresponding values of ω₀ in (2.6); amplitudes a are taken between 0.1 and 9 m and plotted against water depths h₀ between 1000 and 4000 m. (Online version in colour.)

3. Geophysical Korteweg–de Vries equation equation

The system (2.7) of governing equations for equatorial waves serves as a starting point for our derivations. To proceed, we assume the fundamental water wave parameters δ and ε to be small. Our approximate model equations are derived by applying formal asymptotic procedures, where the solutions are assumed to admit power series expansions in the small parameters. We follow the techniques presented in [26,27]. A remarkable feature of system (2.7) is that the parameter δ can be scaled out in favour of ε by the transformation

3.1

where the scaling of v is required to ensure a divergence free flow field in the resulting system. We note that this transformation remains non-singular for ε and δ tending to zero only if these parameters satisfy a certain asymptotic relation, i.e. the transformation (3.1) implicitly implies that we are working in the regime for shallow water waves of small amplitude:

3.2

The result of the transformation (3.1) is system (2.7) but with δ² replaced by ε. By retaining just the leading order terms (i.e. by setting ε=0), one obtains the linear system

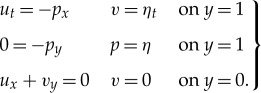3.3

We deduce from (3.3) that the free surface η is described by the linear wave equation η_tt−η_xx=0 whose general solution is of the form 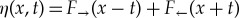, for arbitrary functions 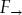and 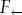. To study the evolution of the right-propagating solution, a certain period of time after it has been generated, we introduce the far-field variables

3.4

Finally, taking into account the transformation (3.1) and rewriting (2.7) in terms of (3.4), the system of governing equations for equatorial waves in the far-field reads

3.5

Note that in order to transfer the free surface to a fixed boundary, we have rewritten the boundary conditions at the free surface by means of Taylor expansions of the involved variables u, v and p about y=1. To obtain an asymptotic solution of system (3.5), we formally expand the respective variables η, u, v and p in the form . At leading order, we obtain the linear system

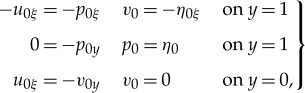3.6

which implies that u₀=p₀=η₀ and v₀=−yη_0x for all y∈[0,1], where η₀=η₀(ξ) is an arbitrary function up to this point. In particular, u₀, p₀ and η₀ do not dependent on the depth y. The first-order system thus reads

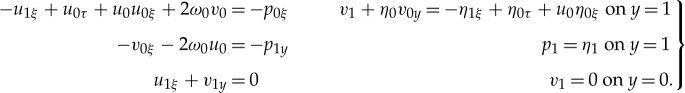3.7

In order to solve this system, we recall that u₀=p₀=η₀ and integrate the second equation in (3.7) with respect to y to obtain . Hence, mass conservation and the first equation yield 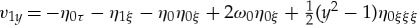. The boundary condition at the flat bed, therefore, yields

3.8

Evaluating (3.8) at y=1 gives

3.9

By combining (3.9) and the first boundary condition in system (3.7), we infer that

Thus, the leading-order approximation for the free surface η, where , satisfies the geophysical KdV equation (gKdV)

with a remainder term of order 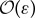presented in the introduction as equation (1.1). We note that at leading-order, the horizontal component of the velocity field u is also described by the same equation (at any fixed depth).

The explicit travelling wave solutions of (1.1) of the form η(x,t)=φ(ξ−cτ) for wave speeds c>0 can be expressed by Jacobi elliptic functions similarly as for the standard KdV equation, cf. for instance [26]. Assuming decay at infinity, the function 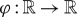given by

3.10

is a travelling wave solution with speed c>0. Note that the Coriolis parameter ω₀ alters the shape of the solution just as the speed c does: when its value increases, the solitary wave becomes taller and narrower, cf. figure 2 and the discussion in [26]. However, the presence of the Coriolis term has a notable impact on the shape of the solution only for sufficiently small wave speeds c: because the constant ω₀ introduced in (2.6) is 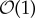, it is clear that for larger wave speeds the profile of the solitary solution (3.10) of gKdV with non-zero ω₀ is almost unchanged compared to the standard KdV solitary wave without Coriolis parameter. For periodic travelling wave solutions, whose explicit expression can be obtained in a similar way, we observe the same behaviour.

Figure 2.

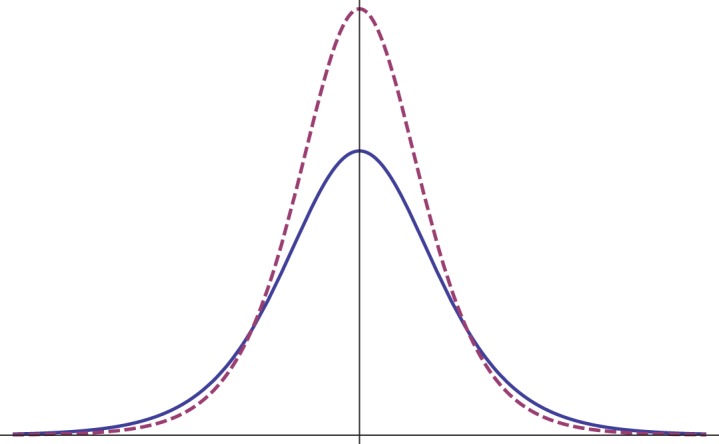
A solitary travelling wave solution of the geophysical KdV equation (1.1) with Coriolis parameter ω₀=0 (plain) and ω₀≈1 (dashed). (Online version in colour.)

4. The near-field versus the far-field

The KdV equation is the paradigmatic example of an integrable equation which embodies soliton theory [29]. It describes a balance between nonlinear and dispersive effects stemming from (3.2). In the previous section, we have seen that this balance occurs for gKdV (as well as for KdV) in the region where the non-dimensional scaled far-field variables satisfy and 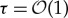. In view of the definition of the far-field variables (3.4) and the scaling (3.1), this region of space can be estimated in original physical variables by 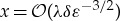. Taking into account the definition of the amplitude and shallowness parameters (2.5) yields that 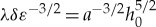. In view of (2.8), we may, therefore, conclude that an estimate for the distance where the balance occurs is approximately 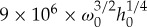. This relation implies immediately that for typical ocean depths of a few thousand metres, the waves would have to travel several thousands of kilometres before a balance could occur. For instance, for an average ocean depth of h≈3500 m and amplitude of about a≈4 m, the balance would be achieved only after roughly 9×10⁴ km—a distance much too large given the size of the Earth.

Looking at the near-field, however, the qualitative picture changes. The region where the non-dimensional scaled near-field variables satisfy 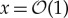and 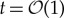can be estimated in original physical variables by 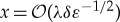in view of the scaling (3.1). Again taking into account the relations (2.5) and (2.8), we find that 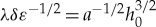. Hence, the balance occurs after a distance of approximately 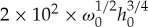. This relation implies for the same choice as taken above, i.e. for h≈3500 m and a≈4 m, that the balance would already occur after approximately 100 km, which is a far more realistic scenario.

In the next section, we proceed by deriving a geophysical model equation for equatorial tsunami waves in the near-field.

5. Geophysical Boussinesq equation

We pursue a derivation of a geophysical shallow water model for small amplitude waves in near-field variables (x,t). In this setting, we require an additional assumption to eliminate the dependence of u on the vertical coordinate y at leading order. To this end, we assume that the flow is irrotational and thus the corresponding dimensionless velocity field satisfies the condition

5.1

Although equatorial flows generally may present non-uniform underlying currents, their effects on the free surface are relatively small, in particular in the shallow water (long wave) regime that we consider here, cf.[2,6,30]. This justifies the irrotationality assumption (5.1).

The starting point for our derivation is the set of governing equations (2.7). We scale out the parameter δ by virtue of the transformation (3.1), which is justified as we are restricting ourselves to the shallow water small amplitude regime characterized by (3.2). Rewriting the boundary conditions at the free surface by using Taylor expansions of the involved functions about y=1 yields

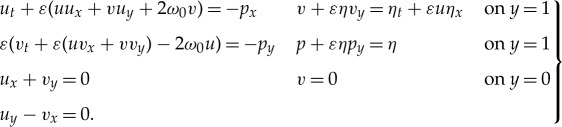5.2

To obtain an asymptotic solution of system (5.2), we formally expand the respective variables and obtain at leading order the linear system

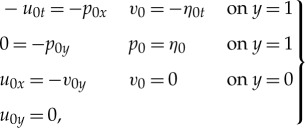5.3

which implies that p₀=η₀ and v₀=−yη_0x for all y∈[0,1] and η_0tt−η_0xx=0. The first-order system, therefore, reads

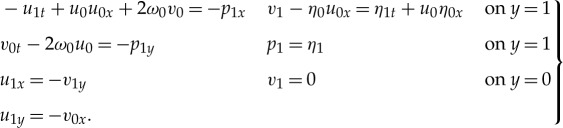5.4

To solve this system, we integrate the second equation in (5.4) and find, using u_0y=0, that 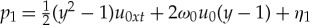. Substituting this in the first equation and differentiating with respect to x, we find that

in view of v_1yt=−u_1xt. Taking the time derivative of the first boundary condition and subtracting the resulting equation from the last expression evaluated in y=1 yields

Expressing 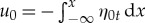and recalling that η_0tt−η_0xx=0, we obtain a Boussinesq type equation in non-local form for the free surface η which holds at order ε, i.e. :

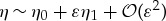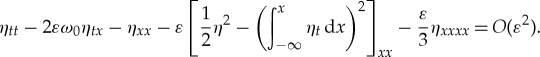5.5

Equation (5.5) can be rewritten in local form using the transformation

5.6

where the corresponding equation for H=H(X,t) is given by

5.7

By means of the scaling

5.8

we obtain from (5.7) the geophysical Boussinesq equation (gBouss),

with an remainder term, which we presented in the introduction as equation (1.2). This equation has explicit travelling wave solutions, which can be represented in terms of Jacobi elliptic functions. To see this, we first assume that the traveling wave φ=φ(x,t)=φ(x−ct), where is a fixed wave speed, and its derivatives decay sufficiently fast to zero at infinity, e.g. . Therefore, φ solves (1.2) if and only if

5.9

where the prime denotes differentiation with respect to the moving frame variable x−ct. It can be directly checked that the function 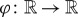given by

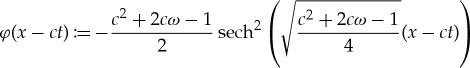5.10

is a solution of (5.9) provided that the wave speed c satisfies

5.11

The explicit expression (5.10) reveals the influence of the Coriolis term on the shape of the traveling wave solutions of gBouss. Similarly to the case of the traveling wave solutions of gKdV, discussed in §3, the presence of ω makes the solitary waves slightly taller and narrower. Finally, we note that an explicit traveling wave solution for the non-local equation (5.5) can be recovered by taking the solution (5.10) and reversing the transformation (5.6).

Remark 5.1 —

The relation

5.12

is the so-called dispersion relation for small-amplitude geophysical shallow water waves, see [23]. It can be found by replacing εω₀ with the dimensionless ω in (5.2) in our derivation of gBouss. The corresponding linearization then yields that η satisfies

5.13

which gives rise to (5.12). In view of (5.10) and (5.11), we conclude that non-trivial explicit solitary travelling wave solutions of gBouss exist only if the wave speed exceeds the geophysical shallow water speed, i.e. c>c₊ for right-moving waves and c<c₋ for left-moving waves.

Remark 5.2 —

We remark that many structural properties known for the standard Boussinesq equation continue to hold for gBouss. For instance, observing that gBouss can be written as the pair of equations

5.14

we immediately obtain the conservation laws

5.15

where the first one corresponds to conservation of mass and the second to conservation of momentum, cf. [26]. In fact, gBouss (as well as gKdV) can be reduced to its classical versions by employing suitable scalings, so that properties like integrability and the existence of infinitely many conservation laws carry over. The effect of the Earth's rotation captured by means of the Coriolis parameter does not alter the overall qualitative features of solutions, but modifies slightly some specific quantitative aspects, as can be seen from the explicit solutions of gKdV and gBouss.

6. Applicability for tsunami modelling

Finally, we comment on the applicability of gKdV and gBouss as models for tsunami wave propagation. Shallow water models have been frequently used to model the propagation of tsunami waves in the open ocean, see for instance the discussions in [31,32]. The shallow water assumption is reasonable as the wavelength of tsunamis is much longer than the average ocean depth. Moreover, the amplitude of a tsunami is very small offshore, typically less than 1 m, so that the smallness assumption on the amplitude is also justified. It has been pointed out in a series of papers that the applicability of KdV as a model for tsunami wave propagation should be questioned; see the discussions in [1,2,33,34]. The main argument is that the balance between nonlinearity and dispersion as embodied by KdV would occur at time and length scales which cannot be realized on Earth. Our analysis in §4 for gKdV shows that the inclusion of Coriolis effects in the model does not alter this fact.

The discussion in §4 shows, however, that gBouss, which was derived in near-field variables as opposed to the far-field variables used for gKdV, may be an appropriate model to study tsunami wave propagation, because the relevant distances required for the near-field balance are more realistic. Our derivation is based on the f-plane approximation, which is applicable in the context of tsunami waves near the Equator. As an example, we mention the 2004 tsunami, which was generated by an earthquake with epicentre off the west coast of Sumatra, Indonesia, and consequently spread across the Indian Ocean in a neighbourhood of the Equator: one wavefront propagated eastward from the fault line, and another front moved in the opposite direction, roughly parallel to the Equator, cf. [30,35,36]. With regard to applications of these equations to tsunami modelling, the equatorial regions in the Indian ocean are of great interest. Also, a broadly taken view is that the largest shallow earthquakes occur in the subduction zones which ring the Pacific Ocean, where also volcanoes abound, and the tsunami hazard throughout the tropical Pacific is, therefore, potentially high. However, the Polynesian islands have typically steep-sided reefs that act as a natural protection against tsunamis. Let us finally remark that, in contrast with the 2004 tsunami, which caused a devastating flood on the coasts of Sri Lanka, the 1883 tsunami generated by the volcanoes at Krakatoa was hardly notable in Sri Lanka, although both tsunamis were triggered in a similar region by comparably strong seismic events. The huge difference in the effects on the coast of Sri Lanka could be explained by the fact that the earlier event happened in the month of August as opposed to the 2004 tsunami which occurred in the month of December when under the northeast monsoon the Equatorial Indian Ocean current propagates along the equator towards Sri Lanka, thus enhancing the effect; see the discussion in [34,35,37–39]. It is, therefore, of interest to investigate the effects of tropical currents on the propagation of tsunami waves in the spirit of [14] taking into account also the influence of the Coriolis effect, see [7,8] for recent discussions of equatorial current fields.

Data accessibility

This article has no additional data.

Authors' contributions

Both authors contributed equally to all parts of the paper.

Competing interests

We declare we have no competing interests.

Funding

R.Q. acknowledges the support of the Austrian Science Fund (FWF), grant no. W1245, and the European Research Council, Consolidator grant no. 682537.