Robust Tests for Single-marker Analysis in Case-Control Genetic Association Studies

Abstract

Choosing an appropriate single-marker association test is critical to the success of case-control genetic association studies. An ideal single-marker analysis should have robust performance across a wide range of potential disease risk models. MAX was designed specifically to achieve such robustness. In this work, we derived the power calculation formula for MAX and conducted a comprehensive power comparison between MAX and two other commonly used single-marker tests, the one-degree-of-freedom (1-df) Cochran-Armitage trend test and the 2-df Pearson Chi-squared test. We used a single-marker disease risk model and a two-marker haplotype risk model to explore the performances of the above three tests. We found that each test has its own “sweet” spots. Among the three tests considered, MAX appears to have the most robust performance.

1. Introduction

In case-control genetic association studies (CCGAS), single-marker analysis, which tests the association between the outcome and an individual SNP, is often used. The following two tests are usually applied in single-marker analysis when there are no other covariates to be adjusted for: the 1-degree-of-freedom (1-df) Cochran-Armitage trend test (CATT) (Klein et al. 2005; WTCCC, 2007) thatcorresponds to the score test derived from an additive disease model (CATTA) (on the logit scale), and the 2-df Pearson Chi-squared test (Chi-2df) that compares the 3-category genotype frequencies between the case and control groups (Yeager et al. 2007). In addition to these two tests, MAX, which takes the maximum of three CATTs derived under dominant, recessive, and additive models as the test statistic, has also been proposed for the association test (Sladek et al. 2007). A detailed definition of each test will be given below. When there are other covariates to be adjusted for, the test corresponding to each of those above can be derived from the standard logistic regression model that models the effect of the genotype coded according to the assumed disease model, with adjustment for the covariates. An important common feature of CATTA, Chi-2df, and MAX is that their 2-sided testing results are independent of the choice of the risk allele.

The significance level (p-value) of CATTA and Chi-2df can be obtained easily according to their theoretical asymptotic distributions. The calculation of the p-value for MAX is a little bit more involved and requires a multiple-integration or permutation procedure (Conneely & Boehnke, 2007; Li et al. 2008a). Although all three tests have been used in recent genome-wide association studies (GWAS) (e.g., Klein et al. 2005; Hunter et al. 2007; Sladek et al. 2007; WTCCC, 2007; Yeager et al. 2007), there is no consensus as to which one is generally preferrable, and also there are few discussions in the literature of the analytic power of MAX or of comparisons of MAX with the other tests. In this work, we derive an analytic formula for calculating the power of MAX. The existence of a power calculation formula for MAX, together with the power formulas that already exist for CATTA and Chi-2df, enables us to conduct a comprehensive power comparison among the three tests.

Comparisons of various single-marker analyses have been reported by several groups (Freidlin et al., 2002, Guedj et al. 2006; Kuo & Feingold, 2008). The uniqueness of this work is to add the promising MAX test to the comparison. In particular we compare the asymptotic powers of these tests under a broad range of single-locus and multi-locus disease models. The comparison results should shed more light on the relative merits of the three considered tests under various disease risk models and provide guidance for the analysis of future CCGAS.

2. Test statistics definition

We focus first on situations where there are no covariates to be adjusted for. Assume that there are r cases and s controls in a CCGAS, and that there are two alleles, G and g, at a given SNP locus with the possible genotypes gg, Gg, and GG. The notations for genotype counts in the case and control groups are given in Table 1. Based upon Table 1, the general form of the CATT can be written as

$$Z_x=\frac{\sqrt{n}{\displaystyle {\sum }_{i=0}^2{x}_i(r_i/r-s_i/s)}}{\sqrt{\frac{n}{r}\left[{\displaystyle {\sum }_{i=0}^2{x}_i^2{\theta }_i-{\left({\displaystyle {\sum }_{i=0}^2{x}_i{\theta }_i}\right)}^2}\right]+\frac{n}{s}\left[{\displaystyle {\sum }_{i=0}^2{x}_i^2{\vartheta }_i-{\left({\displaystyle {\sum }_{i=0}^2{x}_i{\vartheta }_i}\right)}^2}\right]}},$$ (1)

where x=(x₀,x₁,x₂)'is a genotype score vector for the coding of genotypes gg, Gg, and GG, and θ_i=ϑ_i=(r_i+s_i)/(r+s), i=0,1,2 . The genotype score vector x is chosen by the investigator. It should be pointed out that the CATT given by (1) is equivalent to the score statistic testing for the null hypothesis H₀: β=0 derived from the following standard logistic regression that models the effect of genotypes represented by x,

$$\text{log}\frac{\text{Pr}(\text{case}|x)}{1-\text{Pr}(\text{case}|x)}=\alpha +\beta x.$$ (2)

Based upon (2), the three commonly assumed genetic models--recessive, additive, and dominant--correspond to the following assignments of the genotype score vector x:R=(R₀,R₁,R₂)'=(0,0,1)',A=(A₀,A₁,A₂)'=(0,0.5,1)',and D=(D₀,D₁,D₂)'=(0,1,1)', respectively. Among the three CATT tests, Z_x=A , called CATTA, which is derived according to an additive model, is usually preferred over Z_x=D and Z_x=R, as it does not rely on the assumption of a high-risk allele (assuming a two-sided test is performed), and thus this is the version of CATT that is generally used in CCGAS. The p-value for Z_x can be obtained according to the standard normal distribution.

Table 1.

Notation for genotype frequencies

	gg	Gg	GG	Total
Case	r0	r1	r2	r
Control	s0	s1	s2	s
Total	n0	n1	n2	n

If the true underlying disease model is known, the CATT test Z_x is the most efficient. But in reality, the true disease model is unknown. For a more robust test that enjoys a good performance over a wide range of disease models, the following test statistic, called MAX, has been proposed (Freidlin et al. 2002; Sladek et al. 2007; Li et al. 2008a, 2008b):

$$Z_{\text{MAX}}=\text{max}(|Z_{x=R}|,|Z_{x=A}|,|Z_{x=D}|).$$

There are several ways to evaluate the significance level of MAX. For example, the multiple-integration procedure, which is available in R, can be used (Conneely & Boehnke, 2007), and it is computationally feasible in the context of GWAS. A more computationally challenging approach is through a permutation procedure (Sladek et al. 2007). Li et al. (2008a) derived an analytic upper bound that is reasonably accurate for small p-values.

Another robust test is the 2-df Chi-squared test . Using the notations listed in Table 1, we can define the Chi-2df test as

$${\chi }_2^2={\displaystyle {\sum }_{i=0}^2\left[{(r_i-{\mathit{\text{rn}}}_i/n)}^2/({\mathit{\text{rn}}}_i/n)+{(s_i-{\mathit{\text{sn}}}_i/n)}^2/({\mathit{\text{sn}}}_i/n)\right]}.$$ (3)

The significance level of the Chi-2df test can be evaluated through the 2-df Chi-squared $({\chi }_2^2)$ distribution.

3. The formula for power calculation

Under a given disease model, we denote the expected genotype frequencies of (gg,Gg,GG) for cases and controls as (p₀,p₁,p₂) and (q₀ ,q₁,q₂) , respectively. The analytic power calculation for CATTA Z_A can be found in Freidlin et al. (2002) and Pfeiffer & Gail (2003).

The power calculation for the Chi-2df test is also straightforward. Under the significance level α , the reject region is [η,∞) , where η is the 1−α quantile of the 2-df Chi-squared distribution. The Chi-2df test statistic (defined by (3)) in general follows a non-central 2-df Chi-squared distribution (Edwards et al. 2005) under a given disease model, with the non-centrality parameter $\delta =\mathit{\text{rs}}{\displaystyle \sum _{i=0}^2{(p_i-q_i)}^2/({\mathit{\text{rp}}}_i+{\mathit{\text{sq}}}_i)}$, so the power for the Chi-2df test is

$${\beta }_{\text{Chi}-2\text{df}}={\displaystyle {\int }_{\eta }^{\infty }{\displaystyle {\sum }_{k=0}^{\infty }\frac{{(\delta /2)}^k{u}^k{e}^{-\frac{\delta +u}{2}}}{2^{k+1}{(k!)}^2}\mathit{\text{du}}}}$$

Finally, we derive the power calculation formula for MAX. We denote the reject region of MAX under the significance level α by[γ ,∞), where γ (≥0) satisfies Pr_null (Z_MAX ≥γ)=α. Since (Z_R,Z_A,Z_D)' follows a multivariate normal distribution under the null hypothesis with the mean vector of (0,0,0)'and the covariance matrix Δ given by Freidlin et al (2002), we can obtain the threshold γ by solving the following equation:

$${\displaystyle {\int }_{-\gamma }^{\gamma }{\displaystyle {\int }_{-\gamma }^{\gamma }{\displaystyle {\int }_{-\gamma }^{\gamma }\frac{1}{{(2\pi )}^{3/2}\sqrt{\text{det}(\mathrm{\Delta })}}\text{exp}\left\{-\frac{1}{2}(v_R,v_A,v_D){\mathrm{\Delta }}^{-1}{(v_R,v_A,v_D)}^{\text{'}}\right\}{\mathit{\text{dv}}}_R}{\mathit{\text{dv}}}_A{\mathit{\text{dv}}}_D=1-\alpha .}}$$

This can be accomplished easily using an existing function in the R package.

Under the disease model with the expected genotype frequencies (p₀,p₁,p₂) and (q₀,q₁,q₂) in cases and controls, respectively, (Z_R,Z_A,Z_D)'asymptotically follows a multinormal distribution with mean vector μ=(μ_R,μ_A,μ_D)'and covariance matrix Λ. The mean vector is given by

$${\mu }_x=\frac{\sqrt{n}{\displaystyle {\sum }_{i=0}^2{x}_i(p_i-q_i)}}{\sqrt{\left(\frac{n}{r}+\frac{n}{s}\right)\left[{\displaystyle {\sum }_{i=0}^2{x}_i^2{k}_i+}{\left({\displaystyle {\sum }_{i=0}^2{x}_i{k}_i}\right)}^2\right]}},$$ (4)

with the score vector x chosen as (0, 0, 1), (0, 0.5, 1), and (0, 1, 1) for μ_R ,μ_A, and μ_D, respectively, and with $k_i=\frac{{\mathit{\text{rp}}}_i+{\mathit{\text{sq}}}_i}{r+s},i=0,1,2$. The definition for the covariance matrix Λ is more complicated and is presented in the Appendix, as well as its detailed derivations.

The power of the MAX test for the alternative hypothesis H₁ can be written as

$$\begin{array}{ll}{\beta }_{\mathit{\text{MAX}}}=\hfill & 1-{\text{Pr}}_{{\mathbf{H}}_1}(\left|Z_R\right|<\gamma ,\left|Z_A\right|<\gamma ,\left|Z_D\right|<\gamma )\hfill \\ \hfill & =1-{\displaystyle {\int }_{-\gamma }^{\gamma }{\displaystyle {\int }_{-\gamma }^{\gamma }{\displaystyle {\int }_{-\gamma }^{\gamma }\frac{1}{{(2\pi )}^{3/2}\sqrt{\text{det}(\mathrm{\Lambda })}}\text{exp}\left\{-\frac{1}{2}(v-\mu {)}^{\text{'}}{\mathrm{\Lambda }}^{-1}(v-\mu )\right\}{\mathit{\text{dv}}}_R{\mathit{\text{dv}}}_A{\mathit{\text{dv}}}_D,}}}\hfill \end{array}$$ (5)

where v=(v_R,v_A,v_D)'and Λis the covariance matrix.

4. Power comparison

We assume that the case and control sample sizes are r=s=1,000 . We first conduct the comparison under a single-marker disease risk model. We let the minor allele frequency (MAF) f for a particular SNP in the study population be in the range of 5–50%. For the MAF=f, we let the genotype frequencies of (gg, Gg, GG) in the control population, (q₀ ,q₁,q₂) , have the values (q₀ ,q₁,q₂)=((1−f)²,2f(1−_f), f²). This is reasonable for the study of a rare disease in a source population where Hardy-Weinberg equilibrium holds. Let the odds ratios (ORs) for having 1 copy and 2 copies of the high-risk alleles be R₁ and R₂ , respectively. We have $R_2=R_1^2>1$ for an additive model (in the logit scale), R₂ =R₁>1 for a dominant model, and R₂ >R₁=1 for a recessive model. Given (R₁,R₂), we know that the genotype frequencies of (gg,Gg,GG) in the case population (p₀ ,p₁,p₂) are (q₀ ,q₁R₁,q₂R₂)/(q₀+q₁R₁+q₂R₂).

In addition to the single-marker disease risk model, we compare the power of the three single-marker tests under the following 2-marker haplotype risk model. Suppose the disease risk is conferred by haplotypes consisting of two linked markers, with marker #1 having allele types B and b, and with marker #2 having allele types C and c. We designate the haplotype BC as the high-risk variant (corresponding to the high-risk allele in the single-marker risk model). As with the single-marker risk model, we can define the haplotype risk model as dominant, recessive, and additive. For example, if R₁ and R₂ denote the ORs for having one copy and two copies of the high-risk haplotype, respectively, we have $R_2=R_1^2$ for the additive haplotype risk model. To simplify the power comparison setup, we let p₁ be the BC haplotype frequency in the study population and assume the other three 2-marker haplotypes have the same haplotype frequency. We further assume the independence of the two haplotypes within a subject in the study population. In the Appendix, we provide the formula for calculation of (p₀,p₁,p₂) and (q₀,q₁,q₁) , the genotype frequencies of (bb, Bb, BB) in the case and the control populations, respectively.

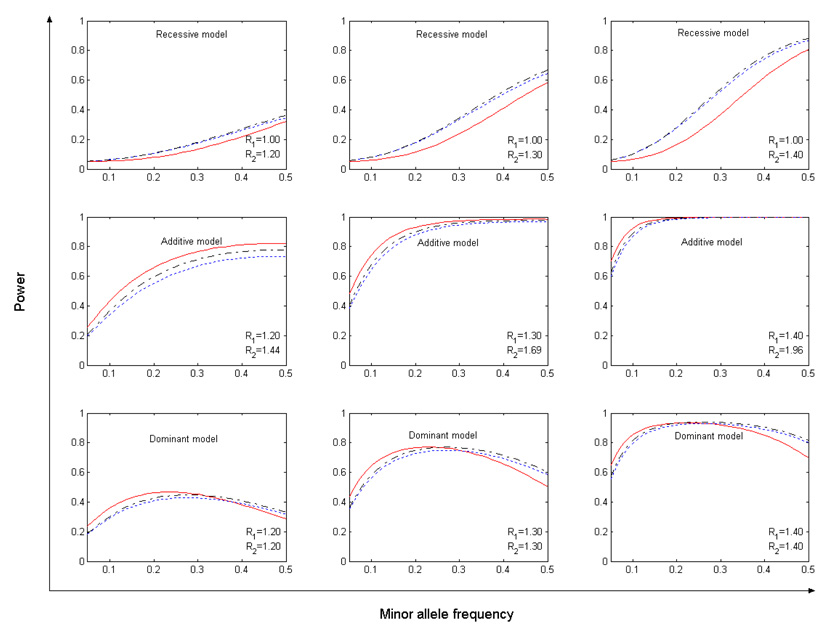
Fig. 1 shows the power curves of the above-considered association tests under each of three commonly assumed single-marker risk models (additive, dominant, and recessive) at a significance level of 0.05. From Fig. 1, we can see that MAX is always more powerful than Chi-2df, and in some cases it is associated with up to a 5% power increase. Comparing CATTA with MAX, we see that CATTA is slightly more powerful than MAX under the additive model, but in most cases the advantage is negligible. Under the recessive model, MAX (as well as the Chi-2df) is noticeably superior to CATTA. Under the dominant model, it is interesting to see that neither CATTA nor MAX dominates the other. CATTA is more favorable when the risk allele is relatively rare, while MAX becomes more attractive as the risk allele frequency gets larger.

Fig. 1.

Power of CATTA (red solid line), Chi-2df (blue dotted line), and MAX (black dash-dot line) under the significance level of 0.05. The number of cases and controls is equal to 1,000. R₁ and R₂ are the odds ratios of 1 copy and 2 copies of the high-risk alleles, respectively.

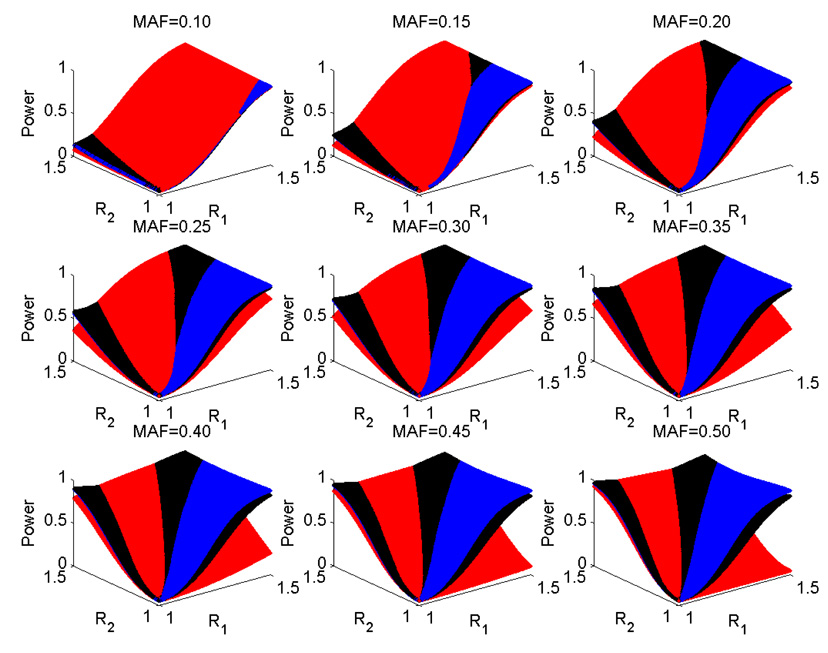
Besides the three commonly used disease models, we also compared the power under a single-marker risk model with all possible combinations of two odds ratios R₁ and R₂ , with each ranging from 1 to 1.5. Fig. 2 summarizes the power comparison results. Clearly, there is no test that can outperform the others in all of the single-marker risk models considered. When the risk allele is relatively rare (say, MAF less than 0.2), all three tests have comparable power under various single-marker models, although CATTA outperforms the others in most of the R₁,R₂ region. As the risk allele gets more common, CATTA becomes less powerful than both MAX and Chi-2df under the single-marker risk model when R₁>R₂, although whether this kind of disease risk model is reasonable is debatable. MAX and Chi-2df have similar performances under all the considered choices of risk models and MAFs, with MAX performing more favorably under the risk model when R₁<R₂, and less favorably when R₁>R₂.

Fig. 2.

Power of CATTA (red), Chi-2df (blue), and MAX (black) under the significance level of 0.05. The number of cases and controls is equal to 1,000. R₁ and R₂ are the odds ratios of 1 copy and 2 copies of the high-risk alleles, respectively. MAF is the minor allele frequency.

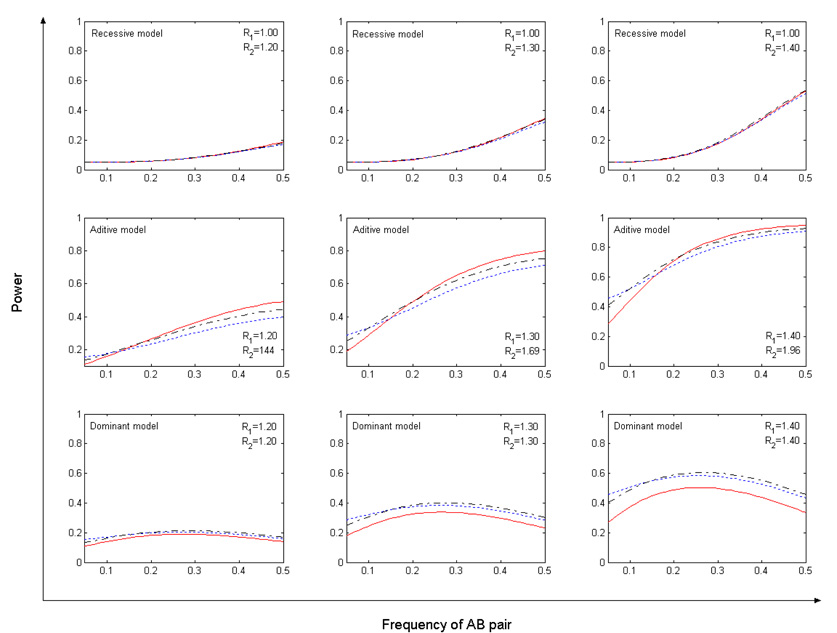
Power comparison results under the 2-marker haplotype risk models are given in Fig. 3. Similar to what we observed in Fig. 1, MAX appears to have the most robust performance. Although MAX is slightly less powerful than CATTA under the additive haplotype risk model, it has a noticeable power advantage over CATTA (more than 10% higher) under the dominant haplotype risk model. Also, from Fig. 3, we notice that MAX is consistently better than the Chi-2df, although the percentage increase in power is limited.

Fig. 3.

Power of CATTA (red solid line), Chi-2df (blue dotted line), and MAX (black dash-dot line) under the significance level of 0.05. The number of cases and controls is equal to 1,000. R₁ and R₂ are odds ratios for one copy and two copies of the high-risk haplotype.

5. Discussion

Choosing the right single-marker analysis is a critical step for the success of CCGAS. Because of the uncertainty about the true underlying disease risk model, robust tests that have good performances under a wide range of disease models are preferred over those that are too sensitive to the model assumptions. MAX was designed specifically to achieve such robustness. Compared with the commonly used CATTA and Chi-2df, the power of MAX is less understood even though its type I error rate has been thoroughly investigated by Li et al. (2008). In this work, we derived the power calculation formula for MAX. Based on this power calculation formula, as well as the ones already existing for CATTA and Chi-2df, we conducted a comprehensive power comparison among the three tests. Not surprisingly, we found that each test has its own “sweet” spots. But MAX appears to have the most robust performances when the underlying genetic models are recessive, additive, or dominant. Under various overdominant models, the Chi-2df and MAX have very similar performance, with the power of the Chi-2df slightly higher than that of the MAX.

In order to assess the statistical significance of MAX, Sladek et al. (2007) used a permutation procedure to estimate p-values of MAX for each SNP. In order to ensure a reliable estimation for any p-value falling below the level of 10⁻⁶, we would need to carry out more than 10⁷ permutation steps. It would be time-consuming and computationally challenging for a large-scale CCGAS. Alternatively, multiple integration (Conneely & Boehnke, 2007) and an efficient approximation method (Li et al., 2008) have been proposed to evaluate the statistical significance of MAX. For the integration procedure (Conneely & Boehnke, 2007), it would be possible to use the R package “mvtnorm”, which could be freely downloaded from the website http://cran.r-project.org/. The efficient approximation approach (Li et al., 2008), which is based on a one-dimensional integral, is user-friendly and can be implemented in many software packages, such as C, C++, R, Matlab, and SAS.

Since the MAX test did not perform as well as the chi-squared test under the overdominant model (R₁>R₂) , we also considered its extension, called MAX4, which is the maximum of four trend tests under four genetic models-- recessive, additive, dominant, and overdominant--with scores (0,0,1), (0,0.5,1), (0,1,1), and (0,1,0), respectively. We conducted some simulation studies to compare the asymptotic power of the MAX4 with that of CATTA, Chi-2df, and MAX. Table 3 showed the results. It can be seen from Table 3 that the MAX4 has the best performance among the four considered tests under the overdominant models, but it is slightly less powerful than the MAX test under the other three models considered. The choice between MAX and MAX4 depends on the likelihood of the overdominant model in real applications.

Table 3.

Power comparison under four genetic models with 1,000 cases and 1,000 controls at the significance level of 0.05

		Minor allele frequency
	(R1,R2)	0.1	0.2	0.3	0.4	0.5
Recessive model	(1,1.3)
	CATTA	0.059	0.114	0.237	0.411	0.584
	Chi-2df	0.080	0.177	0.334	0.506	0.645
	MAX	0.080	0.18	0.345	0.526	0.667
	MAX4	0.078	0.17	0.325	0.501	0.648
Additive model	(1.2,1.44)
	CATTA	0.433	0.658	0.766	0.812	0.820
	Chi-2df	0.341	0.552	0.669	0.722	0.732
	MAX	0.368	0.595	0.714	0.766	0.776
	MAX4	0.362	0.574	0.684	0.733	0.742
Dominant model	(1.3,1.3)
	CATTA	0.643	0.767	0.750	0.656	0.503
	Chi-2df	0.562	0.727	0.746	0.693	0.585
	MAX	0.582	0.749	0.767	0.714	0.604
	MAX4	0.591	0.752	0.763	0.702	0.584
Overdominant model	(1.3,1.1)
	CATTA	0.584	0.627	0.491	0.277	0.106
	Chi-2df	0.544	0.695	0.710	0.668	0.600
	MAX	0.542	0.669	0.650	0.560	0.443
	MAX4	0.566	0.713	0.721	0.670	0.588

When there are covariates to be adjusted for, the corresponding MAX test can be derived from the logistic regression model. Li et al. (2008a) suggested a procedure for evaluating the p-value of the covariate-adjusted MAX test. Although the power comparison was conducted without any adjustment for covariates, we expect similar conclusions will still hold when covariate effects need to be adjusted for.

APPENDIX

APPENDIX A: The Covariance between Z_x and Z_y

Theorem

Let x=(x₀,x₁,x₂) ' and y=(y₀,y₁,y₂) ' be any two score vectors. The asymptotic covariance between Z_x and Z_y can be written as

$${\text{cov}}_{{\mathbf{H}}_1}(Z_x,Z_y)=\frac{n}{{\omega }_x{\omega }_y}{x}^{\text{'}}\left[{\mathrm{\Delta }}_r/r^2+{\mathrm{\Delta }}_s/s^2\right]y$$

where ${\omega }_x=\sqrt{\left(\frac{n}{r}+\frac{n}{s}\right)\left[{\displaystyle {\sum }_{i=0}^2{x}_i^2{k}_i-}{\left({\displaystyle {\sum }_{i=0}^2{x}_i{k}_i}\right)}^2\right]},\text{with}{k}_i=\frac{{\mathit{\text{rp}}}_i+{\mathit{\text{sq}}}_i}{r+s}\text{for}i=0,1,2$ ,

$${\mathrm{\Delta }}_r=\left(\begin{array}{ccc}{\mathit{\text{rp}}}_0(1-p_0)& -{\mathit{\text{rp}}}_0{p}_1& -{\mathit{\text{rp}}}_0{p}_2\\ -{\mathit{\text{rp}}}_0{p}_1& {\mathit{\text{rp}}}_1(1-p_1)& -{\mathit{\text{rp}}}_1{p}_2\\ -{\mathit{\text{rp}}}_0{p}_2& -{\mathit{\text{rp}}}_1{p}_1& {\mathit{\text{rp}}}_2(1-p_2)\end{array}\right),\text{and}{\mathrm{\Delta }}_s=\left(\begin{array}{ccc}{\mathit{\text{sq}}}_0(1-q_0)& -{\mathit{\text{sq}}}_0{q}_1& -{\mathit{\text{sq}}}_0{q}_2\\ -{\mathit{\text{sq}}}_0{q}_1& {\mathit{\text{sq}}}_1(1-q_1)& -{\mathit{\text{sq}}}_1{q}_2\\ -{\mathit{\text{sq}}}_0{q}_2& -{\mathit{\text{sq}}}_1{q}_2& {\mathit{\text{sq}}}_2(1-q_2)\end{array}\right).$$

Proof

Let r⃗=(r₀,r₁,r₂) ' and s⃗=(s₀,s₁,s₂)'. Then we have

$$\begin{array}{l}\begin{array}{ll}\text{cov}(Z_x,Z_y)=\hfill & \frac{n}{{\omega }_x{\omega }_y}\text{cov}\left[{\displaystyle {\sum }_{i=0}^2{x}_i(r_i/r-s_i/s),}{\displaystyle {\sum }_{i=0}^2{y}_i(r_i/r-s_i/s)}\right]\hfill \\ \hfill & =\frac{n}{{\omega }_x{\omega }_y}\text{cov}(x^{\text{'}}\overrightarrow{r}/r-x^{\text{'}}\overrightarrow{s}/s,y^{\text{'}}\overrightarrow{r}/r-y^{\text{'}}\overrightarrow{s}/s)\hfill \\ \hfill & =\frac{n}{{\omega }_x{\omega }_y}{x}^{\text{'}}\left[\text{cov}(\overrightarrow{r},\overrightarrow{r})/r^2+\text{cov}(\overrightarrow{s},\overrightarrow{s})/s^2\right]y\hfill \\ \hfill & =\frac{n}{{\omega }_x{\omega }_y}{x}^{\text{'}}\left[{\mathrm{\Delta }}_r/r^2+{\mathrm{\Delta }}_s/s^2\right]y.\hfill \end{array}\hfill \end{array}$$

APPENDIX B: Two-marker Joint Genotype Frequencies under the Haplotype Risk Model

Suppose the disease risk is conferred by haplotypes consisting of two linked markers, with marker #1 having allele types B and b and marker #2 having allele types C and c. We designate the haplotype BC as the high-risk variant. Denote the haplotype frequencies for BC, Bc, bC, and bc as p₁ , p₂ ,p₃ , and p₄ , respectively. Let R₁ and R₂ denote the ORs for having one copy and two copies of the high-risk haplotype, respectively. We assume that HWE holds in the control group. Table 2 gives the joint genotype frequencies. From the table, we can see that the frequencies of BB, Bb, and bb in the control group at marker #1 are (p₁+p₂)²,2(p₂+p₂)(p₃+p₄) , and (p₃+p₄)², respectively; the frequencies of BB, Bb, and bb in the case group at marker #2 are $(R_2{p}_1^2+2R_1{p}_1{p}_2+p_2^2)/\xi ,2(R_1{p}_1{p}_3+R_1{p}_1{p}_4+R_1{p}_2{p}_3+p_2{p}_4)/\xi$, and (p₃+p₄)²/ξ respectively, where $\xi =R_2{p}_1^2+2R_1{p}_1{p}_2+p_2^2+2{(R_1{p}_1{p}_3+R_1{p}_1{p}_4+R_1{p}_2{p}_3+p_2{p}_4)+(p{}_3+p_4)}^2$.

Table 2.

Two-marker joint genotype frequencies

Genotype pair	Frequency
BBCC	$p_1^2$
BBCc	2p1p2
BBcc	$p_2^2$
BbCC	2p1p3
BbCc	2(p1p4+p2p3)
Bbcc	2p2p4
bbCC	$p_3^2$
bbCc	2p3p4
bbcc	$p_4^2$