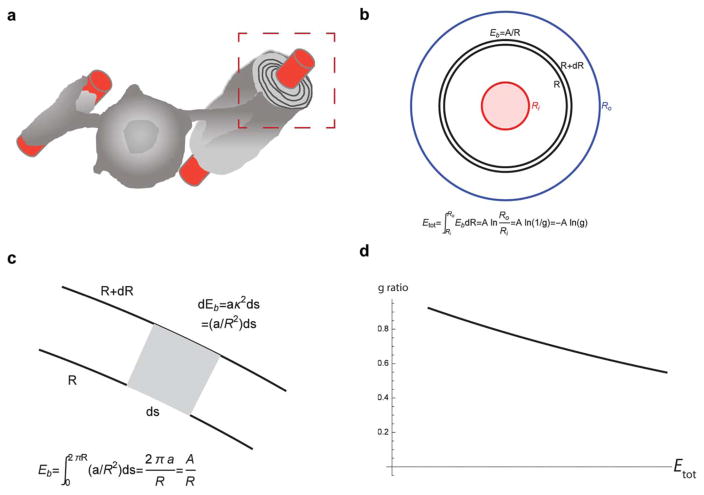
FIGURE 3.

A mechanical model of an elastic myelinated layer around an axon. (A) Mature OL myelinating neuronal axons by extending and wrapping the myelin sheath. (B) A cross section of the axon (pink, red boundary of the radius R_i) and the myelinated layer (white, blue outer boundary of the radius R_o) normal to the axon axis. A thin circular slice of the radius R and width dR (bounded by black curves) stores a bending elastic energy E_b = A/R, where A is constant parameter (explanation in C). The total bending energy E_tot stored in the layer is found by the integration of the slice energy E_b over radius in the range (R_i ≤ R ≤ R_o) and is proportional to the logarithm of g-factor. (C) A small curvilinear sector (gray) inside the thin slice (zoomed inset in B) has bending energy dE proportional to the segment length ds and the square of the local curvature k² =1/R². The energy E_b of the circular slice is found by the integration of dE along the slice, when s changes from 0 to 2πR. (D) The dependence of the g-factor on the maximal elastic energy stored in myelin sheath