Automated detection of photoreceptor disruption in mild diabetic retinopathy on volumetric optical coherence tomography

Abstract

Diabetic retinopathy is a pathology where microvascular circulation abnormalities ultimately result in photoreceptor disruption and, consequently, permanent loss of vision. Here, we developed a method that automatically detects photoreceptor disruption in mild diabetic retinopathy by mapping ellipsoid zone reflectance abnormalities from en face optical coherence tomography images. The algorithm uses a fuzzy c-means scheme with a redefined membership function to assign a defect severity level on each pixel and generate a probability map of defect category affiliation. A novel scheme of unsupervised clustering optimization allows accurate detection of the affected area. The achieved accuracy, sensitivity and specificity were about 90% on a population of thirteen diseased subjects. This method shows potential for accurate and fast detection of early biomarkers in diabetic retinopathy evolution.

1. Introduction

Diabetic retinopathy (DR) is a microvascular disease that affects the 35% of the diabetic population [1, 2] and can cause rapid vision loss. Abnormal retinal perfusion caused by microvascular damage after prolonged periods of high glucose levels can lead to photoreceptor cell death or neovascular complications. For this reason, it is interesting to study photoreceptor integrity in all stages of this disease.

Optical coherence tomography (OCT) [3] is a technology based on the phenomenon of optical interference that has been extensively used to noninvasively image the retinal layers. In cross-sectional OCT images, the main outer-retinal landmarks useful to study photoreceptor integrity are four hyper-reflective regions known as external limiting membrane (ELM), ellipsoid zone (EZ) [4], interdigitation zone (IZ) [5] and retinal pigment epithelium (RPE). The integrity of EZ in particular has been reported to be useful in predicting visual outcomes in various retinal conditions [6–8]. Besides being able to provide a structural description of the retinal layers thickness and integrity in three dimensions, functional additions to OCT such as angiography (OCTA) have been developed in recent years [9]. With the advent of OCTA, depth resolved microvascular imaging of the retina and choriocapillaris has been possible, becoming a powerful tool for clinical assessment of DR [10] as well as other retinal diseases [11–13]. Since structural OCT and OCTA can be acquired simultaneously, they are perfectly registered; therefore, OCT can be an important tool to investigate the anatomic relations between photoreceptor integrity and perfusion.

Clinically, EZ defects can be observed on cross-sectional structural OCT (B-scans) [14]. Detection of EZ disruption has been accomplished by thickness maps [15–17], machine learning methods [18] and en face OCT [16, 19, 20]. En face projections of the EZ slab can provide good contrast for segmentation of healthy and diseased areas as well as potential to detect partial or early-stage atrophy. However, segmentation of EZ defect areas on en face OCT images has only been achieved manually [21] or in a semi-automated manner [22].

EZ disruption is common in numerous retinal diseases, including DR [14]. Although its relationship with loss of visual acuity has been studied in diabetic macular edema [23–26], a detection algorithm sensitive enough to recognize the partial EZ loss and quantify its area in mild DR has represented a segmentation challenge. In this article, we present a fully automated algorithm to identify EZ defect on eyes with mild DR from en face OCT images with simplified layer segmentation requirements. The method assigns membership probabilities to healthy and defect categories on a pixel-level, and quantitatively assesses EZ defect area. The severity of EZ disruption is demonstrated by a color-map. This algorithm was developed on volumetric scans obtained for OCTA, which acquires structural and perfusion information simultaneously. This allows the evaluation of the local relationship between EZ defect region and retinal ischemia.

2. Materials and methods

2.1 Data acquisition

A total of 13 eyes from participants with mild DR and EZ defect (age: 64 ± 11 years old, range: 47-84) and a total of 23 healthy eyes were recruited at the Casey Eye Institute of the Oregon Health & Science University (OHSU). From the 23 healthy eyes, 10 were selected as the normative reference set used in the algorithm development (see section 2.4.2). The other 13 healthy eyes were used for assessing the algorithm’s performance. Written informed consent was obtained from all participants. The study was approved by an OHSU Institutional Review Board protocol and complied with the tenets of the Declaration of Helsinki.

Macular scans were acquired by a 70-kHz, 840-nm-wavelength spectral-domain OCT system (Avanti RTVue-XR, Optovue Inc.). The AngioVue version 2014.1.0.2 software was used to acquire OCTA scans. The OCT data covers a macular area of 3 × 3 mm² with 2 mm depth. The digital sampling interval is 10 × 10 × 3 μm³/voxel. In the fast transverse scanning direction, 304 A-scans were sampled to form a B-scan. Two repeated B-scans were captured at a fixed position before proceeding to the next location. A total of 304 locations in the slow transverse direction were sampled to form a 3D data cube. All 608 B-scans in each data cube were acquired in 2.9 seconds. Structural OCT data was obtained by averaging the two repeated B-scans at the same location. OCTA data was generated from decorrelation of two repeated OCT B-scans using the split-spectrum amplitude-decorrelation (SSADA) algorithm [27, 28]. Two sets of volumetric data were scanned, one x-fast scan and one y-fast scan, registered and merged through an orthogonal registration algorithm (MCT^TM) [29].

2.2 Algorithm overview

The flow chart of the developed algorithm is shown in Fig. 1. First, the structural en face images were constructed by mean reflectance projection of slabs located at the ELM and EZ layers respectively. En face images from two scans acquired in the same visit were registered to reduce inter-scan variation. A ratio image of the ELM and EZ en face images was found to remove shadowing artifacts from inner retinal vessels, vitreous floaters and pupil vignetting, which can confound the detection of the EZ disruption area. The detection of the EZ defect utilized a clustering routine based on a normative ratio image from a set of healthy eyes and a redefined fuzzy membership function. Finally, post-processing based on morphological operations was applied to accurately delineate the EZ defect. The following three sections will describe the process in detail. The algorithm was implemented with custom software written in Matlab 2013a release.

Fig. 1.

Flow chart of the ellipsoid zone (EZ) defect detection algorithm. The pre-processing step generates a ratio image of registered EZ and external limiting membrane (ELM) en face images. The EZ defect detection step first stitches the ratio image under examination to a normative ratio image obtained from the healthy control group, then calculates the optimal number of clusters by a fuzzy c-means algorithm, removes noise by a median filter and finally assigns to each pixel a defect severity degree by a redefined function of membership to the defect category. The post-processing step filters out residual noise and generates the final defect severity map.

2.3 Pre-processing

2.3.1 Identification of EZ boundary location and generation of en face projection images

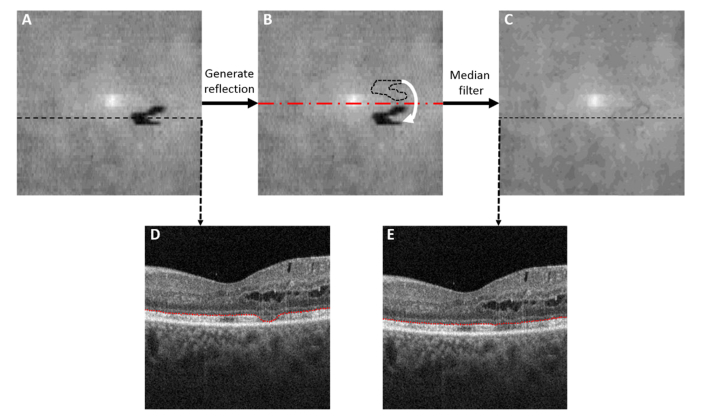
Using directional graph search algorithm [30], we identified the inner limiting membrane (ILM), outer plexiform layer (OPL), the inner boundary of EZ and the Bruch’s membrane in the volumetric scans. This algorithm has been successfully applied in the segmentation of several pathologies such as exudates, epiretinal membrane, cysts, retinal neovascularization and drusen, and its performance has been reported elsewhere [30]. Segmentation of inner retinal boundaries is necessary to create en face projections of inner retinal flow while segmentation of EZ and Bruch’s membrane is necessary for EZ defect detection. While the Bruch’s membrane is not disturbed by the disease and its segmentation by directional graph search is a relatively simple task [31], the segmentation of disrupted EZ poses challenges. Moreover, in order to detect EZ disruption reliably from an en face image, we need to create a thin slab that would contain the EZ, even in areas with local EZ loss without referencing to other structures such as RPE, as they introduce variability not necessarily related to EZ status. The areas with significant photoreceptor loss, however, have a reduced layer contrast of the EZ and the graph search algorithm can fail to identify their boundaries. These regions can be identified by thresholding the EZ/Bruch’s membrane thickness map of the whole scan [Fig. 2(A)] and looking for abnormally thin areas. A theoretical contour of where EZ boundary should be was created by substituting pixels below a thickness threshold by the reflection with respect to a horizontal line crossing the center of the en face image (red dashed line in Fig. 2(B)). If abnormally thin EZ/BM loci were also detected in the pixels located at the reflection positions with respect to both a horizontal and a vertical line crossing the center of the image, the mean thickness of the whole area outside the abnormally thin area was used to correct the EZ segmentation. Finally a median filter of of 5 × 5 pixels was applied to correct abrupt changes in the neighborhood of redefined segmentation boundaries and ensure a smooth EZ curve across the whole scan [Fig. 2(C)-2(E)]. Then, we created ELM and EZ en face images by mean projection of reflectance within 15-um slabs internal and external to the smoothed inner boundary of EZ layer [Fig. 3]. The slab thickness was fixed for all subjects as in Refs [18, 32] and was slightly thinner than the value previously reported for the EZ thickness of a population of healthy subjects [33], in order to minimize the effect of outliers.

Fig. 2.

Routine for detection of inner boundary of ellipsoid zone (EZ) location slab. Firstly, drastic EZ segmentation changes due to large photoreceptor loss are identified by pixels with abnormally low value in an EZ/Bruch’s membrane thickness map (A). Then, the reflection of the EZ segmentation area is generated with respect to a horizontal line crossing the center of the en face image (B) and the EZ location at the pixels below threshold is substituted by the pixels in its symmetric reflection. Finally, a median filter is applied to ensure a smooth EZ segmentation across the whole scan (C). Representative B-scans are shown before (D) and after EZ smoothing (E). As observed in (D), the directional graph search algorithm can properly segment the areas with partial EZ loss but not the areas with total EZ loss.

Fig. 3.

Generation of external limiting membrane (ELM) and ellipsoid zone (EZ) en face images based on the smoothed EZ inner boundary segmentation . (A) A representative B-scan. The red dashed line indicates the smoothed EZ inner boundary. The blue dashed line indicates the boundary position of the slab used to generate the EZ en face image in (B). The yellow dashed line indicates the boundary position of the slab used to generate the ELM en face image in (C).

2.3.2 Registration and merging of two scans

The ELM and EZ en face images were registered with those of a second scan from the same visit in order to reduce inter-scan variation due to differences in signal strength. To recognize the affine transformations that optimize the overlap between en face images of different scans, maximum projection angiograms of the inner retinal flow (between ILM and OPL) were computed and registered first. Then, the same transformation was applied to en face ELM and EZ images of the second scan. Finally, each pair of overlapping images was merged by averaging.

2.3.3 Ratio image

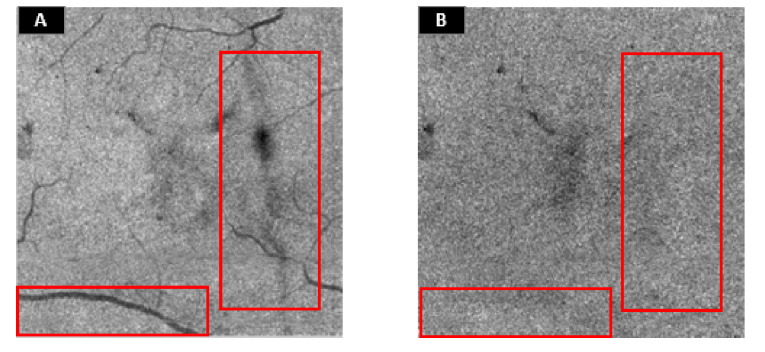
Vessels, vitreous floaters, retinal exudate/hemorrhage and pupil vignetting cause shadowing artifacts on both EZ and ELM en face images, observed as low reflectance objects, hindering the accurate detection of the EZ defect. Since the artifacts exist on both adjacent slabs, and assuming same signal attenuation, shadows may be eliminated by obtaining a ratio of en face images [Fig. 4]. A normalized ratio image was acquired by Eq. (1):

$$R_N=\frac{R}{{\mu }_R+2{\sigma }_R}$$ (1)

where R is ratio image before normalization, ${\mu }_R$is its mean value and${\sigma }_R$is the standard deviation.

Fig. 4.

Illustration of the reduced signal variation on the ratio image. (A) Ellipsoid zone (EZ) en face image. (B) Ratio image. The suppression of shadowing artifacts is shown in the red boxes.

2.4 Detection of EZ defect

After artifact correction, the intensity of the EZ defect in the normalized ratio image is generally lower than the healthy area. The more serious the defect, the lower the region intensity [Fig. 5(A)]. However, the low contrast between defect and healthy areas makes it difficult to define its boundaries [Fig. 5]. Based on these observations, rather than attempting to find hard boundaries, the pixels contained in the defect area can be classified by using fuzzy membership, in which the membership value represents the degree of certainty of each pixel’s belonging to the defect category. In this study, a clustering optimization and a redefined fuzzy membership methods were introduced and implemented.

Fig. 5.

Different damage degree of the ellipsoid zone (EZ) observed on a ratio en face image (A) and a representative B-scan (B). The yellow arrow represents the more severely damaged EZ area; the orange arrow represent the healthy EZ area; the blue arrow represents the slightly damaged EZ area.

In image processing by fuzzy logic, grayscale sets can be divided into a number of clusters, each with a centroid value used by membership functions to determine the belonging degree of pixels to certain categories. In the case of EZ disruption, histogram analysis of the en face ratio images defined above would not help in determining the number of clusters in which the signal could be distributed, a common feature of biomedical images. To overcome this problem, we have developed a fuzzy c-means method that iteratively corrects the membership of pixels into healthy and defective categories by optimizing the number of clusters, until the pixels in a normative ratio image corresponding to a control group with healthy EZ has defect membership equal to zero. Next, we will introduce the rationale for the iterative cluster number detection, redefinition of the membership function and cleanup routine by post-processing.

2.4.1 Fuzzy membership

In this step, a redefined fuzzy membership method was used to derive the degree of affiliation of ratio image pixels to the “defect” category. A fuzzy c-means algorithm was first applied to determine the threshold corresponding to each category, which is then used to evaluate the membership. Fuzzy c-means is a clustering algorithm that classifies a data set with n members$\left(R_j,j=1,\mathrm{2...}n\right)$ into C fuzzy categories by minimizing a fuzzy c-means objective function J with respect to membership $u$ [Eq. (2)]:

$$J={\displaystyle {\sum }_{i=1}^K{J}_i={\displaystyle {\sum }_{i=1}^K{\displaystyle {\sum }_{j=1}^n{u}_{ij}^m{d}_{ij}^2}}}$$ (2)

where $d_{ij}=\Vert c_i-R_j\Vert$ is the distance between the i^th cluster center $c_i$and the j^th data point $R_j$, and m is the fuzzy weighting index [34], in this study m = 2.

The necessary condition for the Eq. (2) to reach its minimum is:

$$c_i=\frac{{\displaystyle {\sum }_{j=1}^n{u}_{ij}^m{R}_j}}{{\displaystyle {\sum }_{j=1}^n{u}_{ij}^m}}$$ (3)

$$u_{ij}=\frac{1}{{\displaystyle {\sum }_{k=1}^K{\left(\frac{d_{ij}}{d_{kj}}\right)}^{\frac{2}{\left(m-1\right)}}}}$$ (4)

where K is the number of clusters. After this step, the thresholds $c_i$and memberships $u_{ij}$were obtained. However, the values stored in variable $u_{ij}$represent the degree of membership with respect of the center of the cluster, which is actually undesirable to describe the severity of EZ defect. In the cluster corresponding to the defect pixels category, the pixels with lowest intensity on ratio images should have the largest degree of membership, i.e. the largest degree of damage, however they don’t because they are not the closest values to the grayscale value of the cluster centroid. To represent the results in a clinically significant manner, we redefined the membership function to the defect category using only the centroids$c_1,c_2$ in Eq. (5):

$$M=\left\{\frac{-\left(R_j-c_1\right)}{c_2-c_1}+1\right\}\times \left[R_j>c_1\right]\times \left[R_j<c_2\right]+\left[R_j\le c_1\right]$$ (5)

where M is the new membership image, $\left(j=1,2\right)$, R represents the ratio image and the statements between brackets equal 1 if the statement is true, otherwise equal 0. By this function, all pixels in the remaining clusters $\left(i=3,\mathrm{4...}K\right)$ have $R_j>c_2$and zero membership to the defect category, while pixels with $R_j<c_1$ have maximum membership.

It should be noted that the number of clusters to distribute the set of pixel intensities of the ratio image is unknown. We formulated a solution by which an iterative process was used to identify the optimal number of clusters for each image (section 2.4.2) and then the thresholds c₁, c₂ corresponding to the clusters with the lowest-valued grayscale centroids were used in the calculation of M.

2.4.2 Identification of the number of clusters

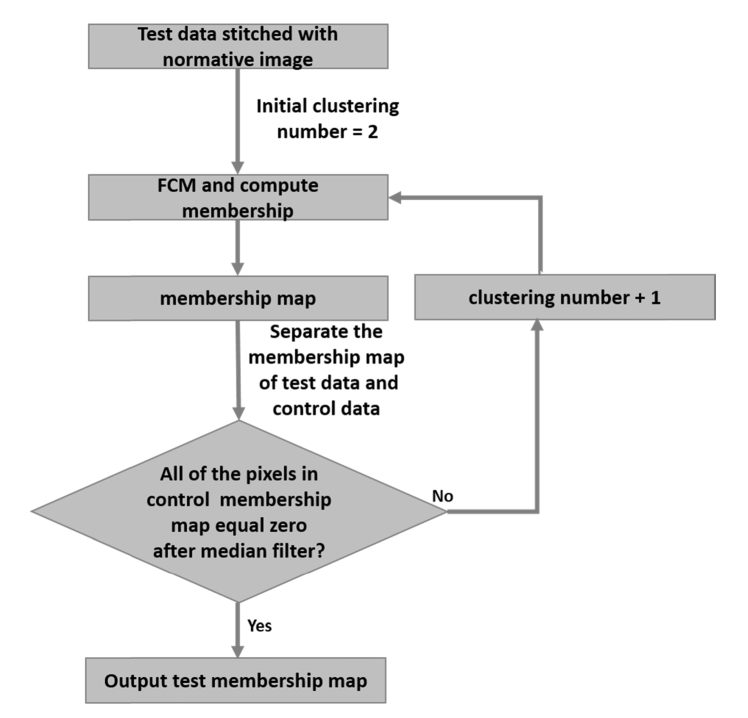
We devised an iterative routine to automatically determine the cluster number for each scan under analysis by minimizing the EZ defect detected on a normative ratio image obtained from a set of healthy eyes [Fig. 6]. First, ten scans were randomly chosen from the control group. The ratio images represented in Fig. 2 were generated for each scan and their average was used as normative ratio image. Then, upon processing a new scan, the normative ratio image was stitched at the bottom of the ratio image under inspection, forming a matrix of 608 × 304 pixels [Fig. 7(A)]. As observed, the upper half of the new image contains an unknown damaged area while the bottom part represents intact EZ area. The initial clustering number was set to 2 and an iterative routine calculated the membership of pixels in the whole image for increasing clustering numbers until the bottom half showed an EZ defect area equal to zero [Fig. 7(B)]. Peripheral noise was removed at each iteration by a 10 × 10 pixels median filter applied on the membership map. The maximum allowed number of iterations was set to 30, given that convergence is not guaranteed. This upper limit was significantly greater than the maximum number of iterations needed for convergence of the population of DR subjects (see Section 3).

Fig. 6.

Iterating routine that calculates the optimal number of clusters to divide the en face ratio data. FCM – Fuzzy c-means.

Fig. 7.

Generation of a defect severity map. (A) The ratio image from a mild diabetic retinpathy scan with an ellipsoid zone (EZ) defect (upper half) is stitched to the normative ratio image obtained from a control group of ten healthy subjects (bottom half). (B) Fuzzy c-means with corrected membership function is applied on image (A) for progressively larger cluster numbers until the bottom half shows a detected area equal to zero. (C) The upper half of image (B) showing the detected EZ defect region, corrupted by peripheral noise. (D) is the defect severity map after cleanup by a median filter.

2.5 Post-processing

Morphological processing was performed on the filtered membership map to remove the abnormally isolated regions with an area of less than 100 pixels.

2.6 Evaluation metrics

Two experienced, masked certified graders (ZW and FR) qualitatively examined B-scan images. Grading was performed two times to assess intra-observer and inter-observer variability. The number of clusters and the defect area detected were assessed for healthy and DR subjects [Fig. 8]. Because the boundaries of EZ defects are not well defined, it is difficult for a grader to accurately delineate them in a single B-scan. To make the grading easier, reliable and still retain good accuracy we regrouped each volumetric data set into 152 subgroups, each consisting of 51 × 8 neighboring A-scans [Fig. 9]. After examining the cross-sectional images of each subgroup, the grader determines whether an EZ defect exists. Manual grading variability was evaluated by the coefficient of variation of the number of subgroups identified on B-scans as EZ defect. Additionally, manual versus automated EZ defect segmentation based on the en face ratio images rather than B-scans was also evaluated. The ratio image on each eye was divided into polar sectors centered on the fovea [Fig. 10], dividing the image into 20 angular slices. The grader identified the slices suspicious of EZ defect.

Fig. 8.

Comparison of the number of clusters (A) and defect area (B) found for the mild diabetic retinopathy (DR) and healthy groups upon either convergence of the iterative cluster optimization routine or reaching the maximum allowed number of iterations. Defect area is given in mm².

Fig. 9.

Comparison of detection of ellipsoid zone (EZ) defect area between the automated algorithm and manual grading on B-scans in five representative diabetic retinpathy (DR) cases. The top row shows the ratio images, the middle row shows the EZ defect area extracted by the proposed algorithm. The bottom row shows the comparison of automatic detection with B-scan manual grading. The red area represents the subgroups where the EZ defect was identified correctly by both the algorithm and the grader. The light blue area represents the EZ defect subgroups detected by manual grading. The dark blue area was the healthy area detected by the manual grader. The yellow area represents the subgroups identified by the algorithm only.

Fig. 10.

Comparison of detection of ellipsoid zone (EZ) defect area between the automated algorithm and manual grading on ratio image. The top row shows the ratio images. The second row shows the manual grading results. Annular regions with EZ defect (red) were differentiated from regions with healthy EZ (green). The bottom row shows the EZ defect area extracted by the fuzzy logic algorithm. DR – Diabetic retinopathy.

Accuracy, sensitivity, specificity [35] and Dice similarity coefficient [36] were used to compare the automated result with manual grading.

The statistical significance of the defect area difference between the populations of healthy and DR subjects was assessed by a one-sample t-test.

The performance of an alternative EZ loss detection method based on thresholding the thickness map generated from the results of the automated layer segmentation on B-scans without corrections were also compared to manual grading results.

3. Results

The required number of iterations (which is equivalent to the number of clusters) varied for each eye, and it was larger for healthy subjects (mean ± standard deviation: 26 ± 4) than for DR subjects (mean ± standard deviation: 5 ± 2) [Fig. 8(A)]. The iterative cluster optimization routine converged for all of the DR subjects analyzed and was inversely correlated to the defect area. The DR subjects with the smallest defect area (subjects # 5, 6 and 8 in Fig. 8(B)) needed the highest number of clusters to converge [Fig. 8(A)], but were still distant from the group of healthy subjects and the upper limit of allowed iterations. While the routine had to be interrupted upon reaching 30 iterations for six healthy subjects, the defect area was negligible compared to DR subjects (A_DR = 1.81 ± 1.17 mm², A_Healthy = 0.01 ± 0.01 mm², p<0.001).

The EZ defect area detected automatically was compared to expert grading of B-scans [Fig. 9] and ratio images [Fig. 10]. Inter-observer variability was 10.4% and intra-observer variability was 9.4% for grader ZW and 8.5% for grader FR. The proposed algorithm agreed very well with manual grading of B-scans and en face images [Table 1]. The performance of an alternative EZ loss detection method based on thresholding of the thickness map generated from the layer segmentation results was also evaluated [Table 2]. Performance of the fuzzy logic method was comparable to a previous method based on machine learning to detect EZ loss in ocular trauma [18] and Dice similarity to manual grading was better than a semi-automated segmentation method for EZ loss detection in retinal telangiectasia based on en face OCT [22].

Table 1. Performance of the proposed algorithm evaluated by manual grading of B-scans and ratio images*.

	Accuracy	Sensitivity	Specificity	Dice similarity
B-scan	0.91 ± 0.06	0.92 ± 0.08	0.87 ± 0.13	0.88 ± 0.07
Ratio image	0.89 ± 0.09	0.91 ± 0.10	0.89 ± 0.17	0.90 ± 0.09

* Mean ± standard deviation

Table 2. Performance of the EZ loss detection algorithm based on thresholding of thickness maps generated from layer segmentation results, evaluated by manual grading of B-scans and ratio images*.

	Accuracy	Sensitivity	Specificity	Dice similarity
B-scan	0.83 ± 0.10	0.53 ± 0.27	0.97 ± 0.03	0.63 ± 0.25
Ratio image	0.84 ± 0.13	0.73 ± 0.30	0.89 ± 0.28	0.79 ± 0.24

* Mean ± standard deviation

We were also interested in investigating the relationship between EZ defect and deep capillary plexus (DCP) integrity. The DCP angiogram was generated by the maximum projection flow within the outer plexiform layer. A projection-resolved OCTA algorithm was applied to prevent shadow artifacts cast by superficial flow onto deeper layers [37, 38]. We observed that the region affected by EZ disruption co-localized very well with areas of reduced capillary perfusion [Fig. 11].

Fig. 11.

Relationship between ellipsoid zone (EZ) defect area and the area with microvascular abnormalities. The top row shows the ratio images. The middle row shows the deep capillary plexus. The yellow boxes indicate areas of reduced capillary perfusion. The bottom row shows the EZ defect area extracted by the proposed algorithm. DCP – Deep capillary plexus.

4. Discussion and conclusion

We have introduced a novel algorithm for automatic detection of EZ defect in DR and identified EZ defect area with a 0.91 detection accuracy and 0.92 sensitivity compared to manual grading. The method relies on the approximate localization of the EZ and ELM slabs and processes the ratio of their mean projections. Classification into defect and healthy tissue categories is performed by a fuzzy c-means scheme with a redefined membership function that assigns to every pixel a probability of affiliation to the defect category.

Previous studies quantifying EZ defect regions have strongly relied on accurate segmentation of EZ slab boundaries, either because they need to generate thickness maps [16, 17, 20] or features used to feed a machine learning classifier [18]. Numerous approaches to solve the problem of delineating layer boundaries in OCT of pathological retinas have been developed successfully, encompassing methods based on directional graph search [30], machine learning and auto-context [39], kernel regression [40] and deep learning [41]. Some pathologies that might appear in advanced stages of DR such as subretinal or intra-retinal fluid pose segmentation challenges in B-scans due to their irregular and unpredictable shapes, but not due to insufficient contrast with surrounding tissue. Contrarily, photoreceptors in mild DR could be either partially lost, preserving some hyper-reflectivity of the EZ layer [42], or displaced on the inner portion and intact on the distal portion [20], in which case EZ reflectivity is only moderately reduced. In any case, it is challenging to accurately mark partial EZ defect on B-scans in early stages of DR. The method proposed here based on en face OCT was sensitive to partial EZ loss, as observed by comparing the area detected in the case of Fig. 9 (DR4) with the representative B-scan shown in Fig. 5(B) and the case of Fig. 9(DR1) with the representative B-scan shown in Fig. 2(D). Moreover, this method is robust to small segmentation inaccuracies. At the same time, en face OCT requires image processing techniques that deal with the numerous confounding shadow artifacts unrelated to the atrophy [21, 22, 43–45], such as the large vessel shadow inaccurately segmented in [Fig. 9 (DR3)].

A distinguishing feature of this algorithm is the incorporation of an iterative routine to calculate the optimal number of clusters needed to distribute the set of pixel intensities. Generally, the task of unsupervised learning an unknown number of clusters is a recurrent challenge in fuzzy c-means image processing applications [46], especially in biomedical imaging due to the high prevalence of noise and artifacts. If clusters are too few, the algorithm would assign an artificially large area to the EZ defect, and vice versa, if clusters are too many, some pixels in the EZ defect area would be lost. Numerous methods have been proposed to solve this issue, such as evaluation of clustering quality by a validity index [47] based on either the degree of separation [48, 49] or the ratio between separation and compactness [50]; finding density peaks [51] and hybrid solutions [52]; but ultimately the optimal clustering method is highly dependent on the application. In our algorithm, we have implemented a novel clustering method that optimizes a compound image formed by the retina under scrutiny stitched to a reference from healthy retinas with characteristics known a priori, attaining a high sensitivity and specificity of EZ defect area.

In order to remove the vessel and image artifacts from the EZ en face image we used the ratio between the mean projection reflectance of adjacent slabs. To successfully remove artifacts without affecting the EZ disruption area, both images need to show the shadows but only one of them should be affected by the disease. The ELM was selected as background to compute the ratio image because it is located at the boundary of the retina and the photodetectors, and early stages of the disease have little effect there, as opposed to the EZ of the photoreceptors. Even in the cases where there is simultaneous loss of ELM and EZ layers, EZ loss could be identified from the ratio image, because in the area of healthy tissue ELM is never as bright as the EZ layer. Most of the vessels and image artifacts could be removed in the ratio operation, however, there were occasions in which large vessels casting a very dark shadow could not be removed entirely, but these cases were rare and easily distinguishable, so they would have little effect on the judgment of EZ disruption.

Besides detecting the EZ defect area, we also represented EZ loss severity by color-coded maps. Conventional fuzzy c-means assigns the highest membership to the values close to the centroid of clusters. However, in our application, where the intention is to represent the severity of the EZ disruption, it is desirable to assign highest membership to the values near the lowest boundary of the cluster representing EZ damage. For this reason, we have used fuzzy c-means to find the centroid of clusters but redefined the membership function to the one in Eq. (5) in order to ensure that membership maps have a reasonable clinical interpretation.

EZ disruption is a gradual process on which boundaries are vague and difficult to define. Also, the EZ slab has varying reflectivity [32] and additional factors such as low signal quality can make it harder for the grader to manually segment the boundaries of defect regions. For this reason, in order to evaluate the method’s accuracy we compared the EZ defect segmentation to a rough approximation of the manually segmented area rather than the exact area overlap. The cases shown in Fig. 9 and Fig. 10 seem to overlap reasonably with the area apparent to a human grader.

In summary, we developed an automated algorithm to detect partial and total photoreceptor loss by evaluating EZ defect areas in en face OCT images of early DR. The method incorporates two novel features: a redefined fuzzy c-means membership function that allowed truly representing disruption severity and an unsupervised automatic clustering routine that permitted accurate mapping of the defect area. The areas affected by EZ disruption appear to exhibit a relationship with capillary perfusion loss in the deep vascular plexus, suggesting a great potential for evaluation of disease evolution using both OCT and OCTA information.

Funding

This work was supported by grants R01EY027833, DP3 DK104397, R01 EY024544, P30 EY010572 from the National Institutes of Health (Bethesda, MD), an unrestricted departmental funding grant and William & Mary Greve Special Scholar Award from Research to Prevent Blindness (New York, NY) and National Natural Science Foundation of China (61471226), Natural Science Foundation for Distinguished Young Scholars of Shandong Province (JQ201516), China Scholarship Council, China (201608370080); and Taishan scholar project of Shandong Province.

Disclosures

Oregon Health & Science University (OHSU), Yali Jia, and David Huang have a significant financial interest in Optovue, Inc. Miao Zhang is an employee of Optovue, Inc. These potential conflicts of interest have been reviewed and managed by OHSU.