Abstract
Purpose
To introduce and evaluate a fully automated renal segmentation technique for glomerular filtration rate (GFR) assessment in children.
Methods
An image segmentation method based on iterative graph cuts (GrabCut) was modified to work on time-resolved 3D dynamic contrast enhanced MRI datasets. A random forest classifier was trained to further segment the renal tissue into cortex, medulla and the collecting system. The algorithm was tested on 26 subjects and the segmentation results were compared to the manually drawn segmentation maps using the F1-score metric. A two-compartment model was used to estimate the GFR of each subject using both automatically and manually generated segmentation maps.
Results
Segmentation maps generated automatically showed high similarity to the manually drawn maps for the whole-kidney (F1 = 0.93) and renal cortex (F1 = 0.86). GFR estimations using whole-kidney segmentation maps from the automatic method were highly correlated (Spearman ρ=0.99) to the GFR values obtained from manual maps. The mean GFR estimation error of the automatic method was 2.98±0.66% with an average segmentation time of 45 seconds per patient.
Conclusion
The automatic segmentation method performs as well as the manual segmentation for GFR estimation and reduces the segmentation time from several hours to 45 seconds.
Keywords: Renal Segmentation, Machine Learning, Glomerular Filtration Rate, Dynamic Contrast Enhanced MRI
Introduction
Chronic kidney disease (CKD), a disease causing gradual loss of kidney function, affects 26 million patients in the US alone (1). Although CKD has a lower prevalence rate among children (1.5 to 3 per 1,000,000), they are particularly vulnerable to the complications caused by this disease such as growth retardation, renal osteodystrophy, and anemia (2). Although initially asymptomatic, CKD can lead to kidney failure, if left undetected or untreated, which necessitates dialysis and eventually a kidney transplant. Progression of CKD to end-stage renal failure can be prevented by early detection and treatment. CKD in children is primarily caused by obstructive uropathy, vesicoureteral reflux, and congenital anomalies that can be diagnosed by renal ultrasound (3). However, reduced kidney function can still be observed in the absence of anatomical anomalies. Magnetic resonance imaging (MRI) provides a more comprehensive anatomical and functional assessment of kidneys, which is often needed to diagnose CKD. Unlike computed tomography (CT) and nuclear scintigraphy, MRI is particularly attractive for pediatric urography as no ionizing radiation is involved.
In the last decade, dynamic contrast enhanced MRI (DCE-MRI) techniques have been used to visualize the renal contrast uptake dynamics and to measure quantitative metrics of renal function such as renal transit time and split renal function (4–6). In DCE-MRI, a patient is administered a gadolinium-based contrast agent intravenously and the in-vivo distribution of the contrast agent is observed by taking a series of T1-weighted MR images over time. The qualitative analysis of these time-resolved MR images helps detection of obstructive and congenital abnormalities, whereas quantitative analysis helps in the assessment of renal function. Pharmacokinetic models have been developed (7–10) to extend the quantitative analysis of DCE-MRI by estimating the glomerular filtration rate (GFR), a primary indicator of renal function used for diagnosing chronic kidney disease. In addition to the high spatial resolution requirement for obtaining diagnostic quality images, tracer kinetics modeling requires DCE-MRI images to have a high temporal resolution (11). Several MRI sequences that can achieve high spatiotemporal resolution needed for quantitative MR urography have been developed (12–19). Some of these sequences have been used in clinical studies for GFR estimation such as TWIST (19), DISCO (20) and stack-of-stars (21). Recently, a free-breathing 3D DCE-MRI sequence based on radially ordered Cartesian k-space sampling, VDRad (Variable Density sampling and Radial view-ordering) (13), was demonstrated for renal dynamic imaging in children using a low-rank constrained reconstruction method (22).
The pharmacokinetic models used for GFR estimation require signal intensity-time curves of the kidneys, which can be obtained from the DCE-MRI data using renal segmentation maps. Manual segmentation of the kidneys can take several hours (23) and often requires trained personnel increasing the overall cost of quantitative analysis. Usually, image segmentation is performed on static images using image-processing techniques. In DCE-MRI, the volumetric images have a temporal dimension that can be leveraged in segmentation. Several techniques have been developed to automate the renal segmentation process using information from spatial only (23–26) and temporal only (27–31) domains. Several techniques have utilized both spatial and temporal domains (32–34) to perform renal segmentation. Some of these techniques (32,34) have been demonstrated on a small number of datasets successfully however their performance on a larger population is unknown. Only one study (23), with 22 clinical datasets, has reported the automatic segmentation performance in terms of GFR estimates. However, it is limited to the spatial information only and requires manual intervention to select seed regions for segmentation.
In this study, we present an automatic renal segmentation method based on computer vision and machine learning. The novel approach utilizes both spatial and temporal domains to achieve full kidney and renal cortex segmentation. We demonstrate the method in a clinical application by obtaining renal segmentation maps and estimating the single-kidney GFR using a 2-compartment model (10). The results are compared to the GFR estimates obtained from manually drawn segmentation maps.
METHODS
Overview of Automatic Segmentation
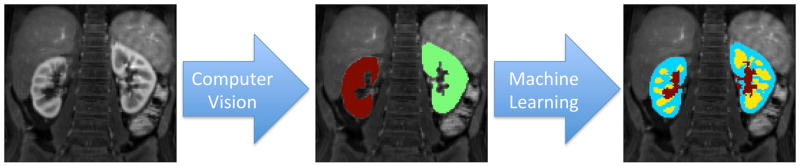
The goal of the proposed method is to create renal segmentation maps for pharmacokinetic analysis. The segmentation process is performed in two steps as visualized in Fig. 1. The first step uses image processing and computer vision methods to automatically locate the kidneys in the abdominal image and segment out the renal parenchyma as a whole. The second step uses machine learning to classify the kidney voxels as cortex, medulla or collecting system.
FIG. 1.
Automatic segmentation overview. First, kidneys are located in the abdominal images using computer vision techniques. Then, each kidney voxel is classified as cortex, medulla or collecting system using machine-learning methods.
Automatic Segmentation of Renal Parenchyma
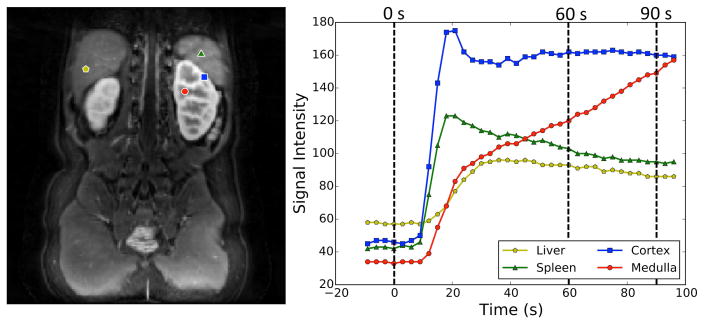
In DCE-MRI, different tissues often show different enhancement characteristics (Fig. 2). Tissues that enhance due to the perfusion of contrast-rich blood such as liver, spleen and renal cortex show an increase in the signal intensity within the first 30s of the bolus arrival followed by a steady decrease in the following temporal phases. Renal medulla, on the other hand, has a steady increase in signal intensity between 30s and 120s due to the accumulation of contrast agent in the renal tubules. In addition to this accumulation due to continuous filtration of the blood, the renal medulla contains the loop of Henle where the contrast agent concentration is increased due to reabsorption of water. These features give the renal medulla a unique intensity-time curve distinguishing it from other tissues (Fig. 2). A similar argument can be made for the collecting system as it enhances at a much later stage.
FIG. 2.
Signal-time curves of the renal tissues and the neighboring organs. Medulla signal keeps increasing in the 60–90s interval due to the accumulation of contrast agent in the renal tubules.
The following scoring metric (Eq. (4)) was used to locate the medulla in the abdominal images (Fig. 3a).
FIG. 3.
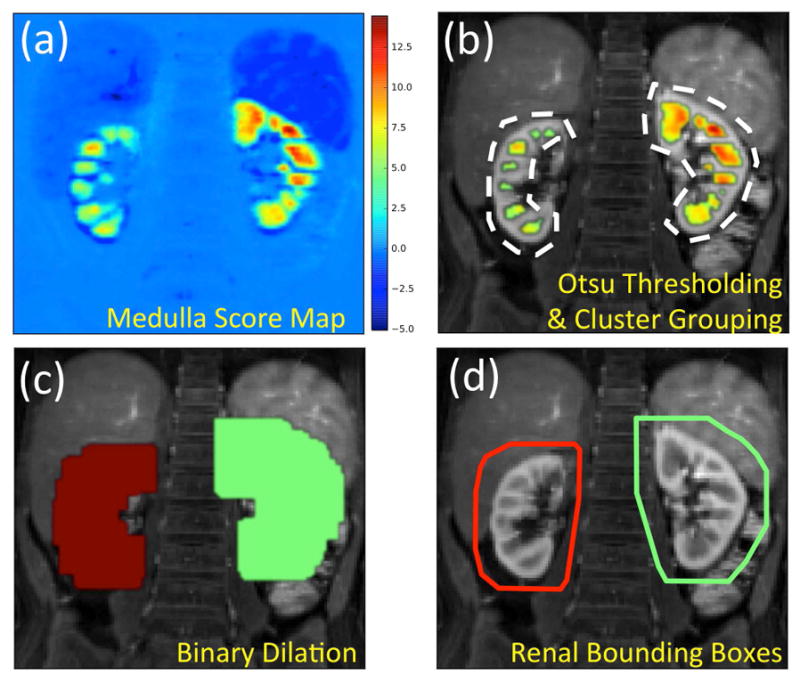
Detection of renal bounding boxes. (a) Distribution of medulla scores in the abdominal image. The scores are whitened by removing the mean and normalizing the standard deviation. The values are the number of standard deviations from the mean score. (b) Scores above the Otsu threshold overlaid on the anatomical image. Clusters within a maximum cortical thickness distance from each other grouped together under the same color. (c) Medulla groups are dilated by the maximum cortical thickness to cover the renal parenchyma. (d) 3D convex hulls of the dilated medulla groups are calculated to create renal bounding boxes.
| [1] |
| [2] |
| [3] |
| [4] |
where SI(t) is the signal intensity at time t and is the pre-contrast signal scaled to 0–1 range. The bolus arrival time (t = 0) is automatically detected from the DCE-MRI dataset as the time point when a total signal increase (across the whole image) of 5% is observed over the baseline. The first multiplication term in the enhancement score (Eq. (1)) rewards the tissues that enhance after the first minute and penalizes the tissues with a signal decrease in the same period. The second multiplication term eliminates the tissues that do not show enhancement in the first minute. The spatiotemporal score (Eq. (2)) is used for evaluating the surrounding tissues based on their enhancement rates. For each voxel the time-to-90% enhancement above the pre-contrast signal level is calculated and the dynamic range is scaled to 0–1 range to create the scaled time-to-90% enhancement maps (T̂90%). Then, spatial grayscale closing operation (●) is performed on the reversed map (1 − T̂90%) using a cube-shaped structuring element (SE) with side length of dctx. The cortical thickness parameter (dctx) is chosen as 11 mm, the maximum cortical thickness reported in the literature (35). The closing operation is performed in two steps: dilation and erosion. In the dilation step, each voxel in the map takes on the maximum value observed in their neighborhood defined by the structuring element. In the erosion step, which is performed on the output of the dilation, each voxel takes on the minimum value within the same neighborhood. The closing operation is used to close the spatial gaps of low score (e.g. medulla) within high score regions of the map (e.g. cortex). Hence, the spatiotemporal score of the medullary regions depends on the speed of cortical enhancement. A high spatiotemporal score indicates a voxel surrounded (within dctx radius) by neighboring voxels that peak in the early phases. These voxels are typically medullary voxels as they are nearly surrounded by renal cortex, which reaches its peak level at a much earlier time-point and receive a higher 1 − T̂90% weight. Pre-contrast score (Eq. (3)) is used for penalizing the voxels that have high signal intensity in the pre-contrast phase such as fat tissue.
A bounding box was calculated for each kidney using the following steps. First, the medulla score maps (Fig. 3a) were thresholded using Otsu’s method (36) to reveal the medulla clusters (Fig. 3b). Then, the clusters within one cortical thickness (dctx) distance in all directions were grouped together (Fig. 3c). Finally, a binary dilation operation was performed to expand the medulla clusters by one cortical thickness (dctx) in all directions (Fig. 3d) and the 3D convex hull was calculated (Fig. 3e) to obtain a bounding box around each kidney (Fig. 3f).
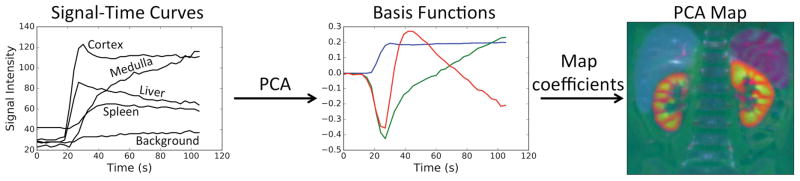
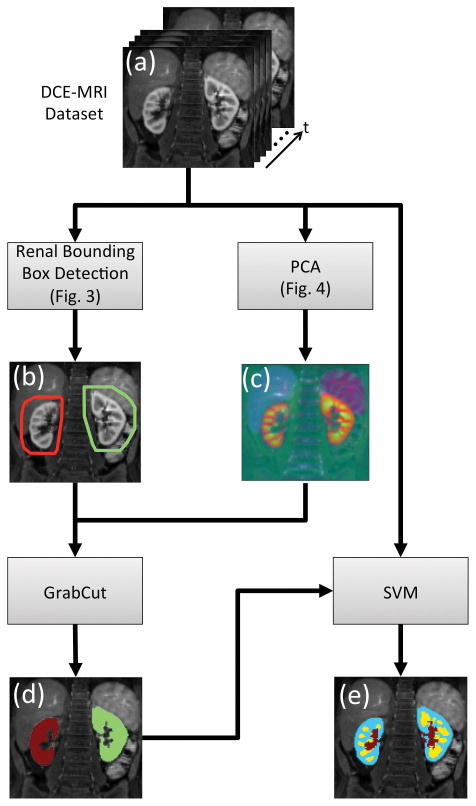
We developed a modification of GrabCut (37) to apply it to DCE-MRI data. The developed algorithm was used to extract the renal tissue from the bounding box defined in the previous step. The GrabCut algorithm uses iterative graph cuts to extract the foreground object from an RGB image given a loosely drawn bounding box around the foreground object. In a typical graph cut segmentation (38), some regions of background and foreground object have to be labeled by an expert. In the recent GrabCut algorithm (37), anything outside the bounding box is considered “background” and the region inside is considered “unknown.” The “unknown” region is labeled as “possible foreground” and “possible background” through iterative graph cuts where the pixel-to-pixel smoothness term is based on the Euclidian distance in the color space. In order to apply this method to the DCE-MRI data, we have modified the GrabCut implementation available in OpenCV to apply the smoothness term in a 3D neighborhood. This modification allowed the use of 3D images with three channels (RGB). The temporal dimension of DCE-MRI datasets often has more than three temporal phases. The temporal phases of the dataset were reduced to three channels using principal component analysis (PCA) and mapped to RGB channels (Fig. 4). The output of the PCA reduction was a 3D-RGB image (3 spatial and 1 color dimensions) where different colors represent different signal-time curve principal components. The modified GrabCut algorithm was applied to the PCA reduced datasets using the renal bounding boxes to obtain the segmentation map of the renal parenchyma (Fig. 5).
FIG. 4.
Basis functions (eigenvectors) corresponding to the highest three eigenvalues are calculated from the subjects signal-time curves. Each voxel’s signal-time curve can be represented as a linear combination of basis functions. The coefficients are assigned to RGB color channels to create the PCA map.
FIG. 5.
Flowchart of the automated segmentation process. (a) Input to the algorithm is the time resolved 3D DCE-MRI dataset. (b) Renal bounding box calculated using the steps described in Fig 3. (c) PCA is applied to the DCE-MRI dataset along the time axis to reduce it to 3 channels represented as RGB. The resulting image has no temporal phases however it still has temporal information (i.e. different colors map to different signal-time curves). (d) Output of the renal parenchyma segmentation using GrabCut. (e) Output of the voxel level SVM classifier for segmentation of renal cortex (blue), medulla (yellow) and the collecting system (red).
Automatic Segmentation of Renal Cortex
The renal voxels detected by the GrabCut algorithm in the previous step were classified as cortex, medulla and the collecting system using machine learning. A random forest classifier was trained using 10,000 randomly selected renal voxels from 11 datasets with manually labeled ground truth segmentation maps.
Each voxel was represented by 7 features:
Signal intensity (SI) at t = 0,30,60,90,120,150 seconds
Depth of voxel within renal tissue (determined from the whole-kidney mask obtained from GrabCut)
In order to reduce inter-subject variability, each signal intensity feature was whitened by removing the mean feature value of all voxels and dividing by the standard deviation of all voxels that belong to the same subject. After whitening, the distribution of the voxels for each feature was centered on zero with a standard deviation of one. This led to voxels being evaluated based on their relative signal intensity with respect to the other voxels in the same subject. The feature selection process and evaluation of feature effectiveness can be found in the supporting document (Supporting Table S1).
Hyper-parameters of the classifier were determined from the training set using a grid search with 5-fold cross-validation. The trained random forest classifier was tested on 915,000 kidney voxels that are not included in training dataset. The classification performance of the random forest model was compared to the SVM and AdaBoost (with decision tree) models using a small sample set of 10,000 randomly chosen voxels with a 50% train-test split.
Evaluation of Segmentation Maps
The segmentation maps obtained from the automatic segmentation algorithm were compared to the manually obtained segmentation maps by using F1-score, the harmonic mean of precision (positive predictive value) and recall (true positive rate or sensitivity) (Eq. (5)).
| [5] |
The F1-score metric is in the range [0, 1] where a complete overlap between the true segmentation map (manual segmentation) and the predicted segmentation map (automatic segmentation) corresponds to an F1 score of 1.0 and a complete mismatch corresponds to a score of 0.
Pharmacokinetic Analysis
Glomerular filtration rate (GFR) estimation using compartmental models requires an arterial input function (AIF) and the concentration–time curves of the contrast agent within a region of interest (ROI) encompassing kidneys. The ROI needed for subject-specific AIF calculation is obtained by manual selection of arterial voxels in the common iliac artery right below the aortic bifurcation. The renal ROIs are obtained by both manual and automatic segmentation of kidneys.
Contrast agent concentration within each voxel (Cvoxel) is calculated using Eq. (6). The T1 value of the voxel is estimated from the measured signal (SIvoxel) using the steady state spoiled gradient (SPGR) signal model described in Eq. (7).
| [6] |
| [7] |
where r1 is the relaxivity of gadolinium, T1(0) is the pre-contrast T1 value of the tissue, TR is the repetition time and θ is the flip angle. The scaling constant S0 is calculated for each voxel by solving Eq. (7) at time zero using the pre-contrast T1 values. The repetition time and flip angle are obtained from the data acquisition protocol. The rest of the parameters are assumed to be r1 = 4.5 (mMs)−1, T1(0) = 1.9 s for blood, and T1(0) = 1.2 s for kidney tissue as reported in literature (39, 40).
The concentration in kidney (Ckidney) and the arteries (Cartery ) are obtained by averaging the voxel concentrations (Cvoxel) within the corresponding renal and arterial ROIs. A hematocrit correction is applied to the arterial concentration to get the contrast agent concentration in the plasma using Eq. (8).
| [8] |
A large vessel hematocrit (Hctlarge) value of 0.41 is used for the hematocrit correction of arterial concentration (10).
The average concentration within the kidney ROI (Ckidney) is modeled using a 2-compartment model (10). The model assumes that the kidney tissue is made of two compartments, an arterial and a tubular compartment. The model uses the AIF and the measured kidney concentration to calculate the transfer coefficient (ktrans) between these two compartments, which is proportional to the filtration rate. Only the first 90s of the concentration-time curves is used in the fitting to guarantee that the contrast agent does not leave the ROI as assumed by the model (10). Single-kidney GFR is calculated from the ktrans estimates using Eq. (9).
| [9] |
where Vkidney is the total kidney volume.
Study Design
With Institutional Review Board approval and waived consent, we retrospectively identified three different groups of datasets with different protocols that were suitable for automatic renal segmentation. All clinical scans were performed on a 3T MR750 scanner (GE Healthcare, Waukesha, WI) using a 32-channel torso coil.
Group 1
This group consists of 11 consecutive pediatric subjects clinically referred for contrast-enhanced MRI. The acquisition protocol with fast contrast injection used in this group was the same as the protocol used in the vast majority of our abdominal DCE-MRI exams. A single dose 0.03 mL/kg gadobutrol contrast was diluted in saline to a volume of 10 mL and power injected intravenously at a rate of 1 mL/s followed by 20-mL saline flush at the same rate. Acquisitions were performed using respiratory navigated VDRad (13) with fat saturation: TR=3.3 ms, FA=15°, ±100kHz bandwidth, matrix=192×180, FOV=320×256 mm, thickness=2.4 mm, 80 slices, 36 temporal phases, 3s temporal resolution and 6.2× acceleration. Images were reconstructed using a low-rank method based on ESPIRiT compressed sensing and parallel imaging (22).
Group 2
This group consists of 11 consecutive pediatric subjects clinically referred for contrast enhanced MRI. This dataset was acquired with the same protocol as Group 1 but the contrast injection rate was slowed down for renal functional studies. A single dose 0.03 mL/kg gadobutrol contrast was diluted in saline to a volume of 10 mL and power injected intravenously at a rate of 0.3 mL/s followed by 20-mL saline flush at the same rate. Acquisitions were performed using respiratory navigated VDRad (13) with fat suppression: 50 temporal phases, and 7s temporal resolution. Images were reconstructed using the same low-rank method (22).
Group 3
This group consists of four consecutive pediatric subjects clinically referred for contrast enhanced MRI. The acquisition technique of this dataset uses a different sampling method and a different method of obtaining fat suppression than Groups 1 and 2. The contrast agent dose and injection rate were the same as Group 2. Acquisitions were performed using respiratory triggered DISCO (16) with parameters: TR=3.9 ms FA=12°, ±167kHz bandwidth, matrix=256×200, FOV=280×280 mm, thickness=2.6 mm, 34 slices, 35 temporal phases, 12s temporal resolution and 2.5× Autocalibrating Reconstruction for Cartesian (ARC) acceleration. In this dataset, the fat-water separation is obtained using 2-point Dixon technique.
In total, this study has 26 subjects with an average kidney volume of 113±11.6 mL. Four cases of hydronephrosis, two cases of unilateral renal hypoplasia, and one case of renal ectopia were observed in the dataset. From the DCE-MRI datasets, 45 kidneys (7 subjects had only a single kidney – 5 right and 2 left) were manually segmented by a trained post-processing technologist. The segmentation maps generated by the automatic method were compared to the manually segmented ROIs using precision and recall metrics as well as F1-score.
In this study, the pharmacokinetic analysis was performed on the renal parenchyma. The segmentation maps generated by manual and automatic segmentation were used to calculate the single-kidney glomerular filtration rates GFRmanual and GFRauto respectively. Single-kidney GFR estimates from the automatic segmentation maps are compared to the GFR estimates from the manual segmentation using the GFR estimation errors (Eq. (10)) and the right kidney split functions (Eq. (11)).
| [10] |
| [11] |
The robustness of the segmentation algorithm with respect to the cortical thickness parameter was evaluated on group 1 subjects. Automatic segmentations were performed for cortical thickness parameters (dctx) between 1 mm and 14 mm for each subject. The resulting renal segmentation maps were compared to the manual segmentation maps to obtain an average F1-score for each assumed cortical thickness.
Processing Time
Running time of the automated algorithm was obtained on an Apple MacBook Pro with 2.7 GHz dual-core processor and 16GB memory running OS X. All processing was done using Python and C++ libraries. The run time was calculated by running the algorithm on 11 datasets from group 1 and averaging the time it takes to compute the segmentation masks. The data loading time was excluded from the calculations. The datasets used for timing each had a 192 × 180 × 100 matrix with 36 temporal phases.
RESULTS
Image Acquisition
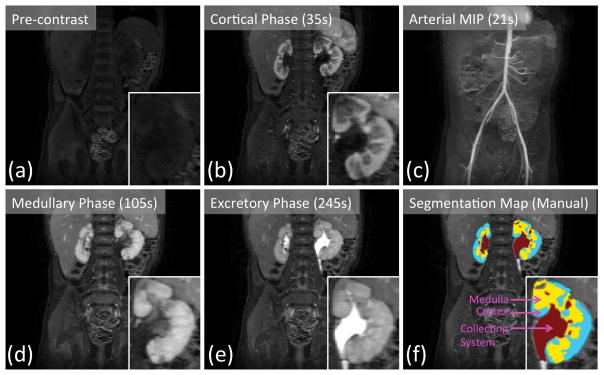
An example of the DCE-MRI dataset acquired using respiratory navigated VDRad at 7s temporal resolution is shown in Fig. 6. The butterfly navigation incorporated into VDRad resulted in diagnostic quality images with no apparent respiration-induced artifacts. The temporal resolution of the acquisition was high enough to capture the cortical enhancement phase of the contrast update (Fig. 6b) as well as the arterial enhancement phase (Fig. 6c). Manually drawn segmentation maps of the kidneys are shown in Fig. 6f.
FIG. 6.
Renal pre-contrast (a) and post-contrast (b, d, e) phases captured by 7s temporal resolution VDRAD acquisition. (c) The arterial phase can be observed in the maximum intensity projection (MIP) image. Manually drawn segmentation map (f) is used as the ground truth labeling of the renal voxels.
Automatic Renal Segmentation
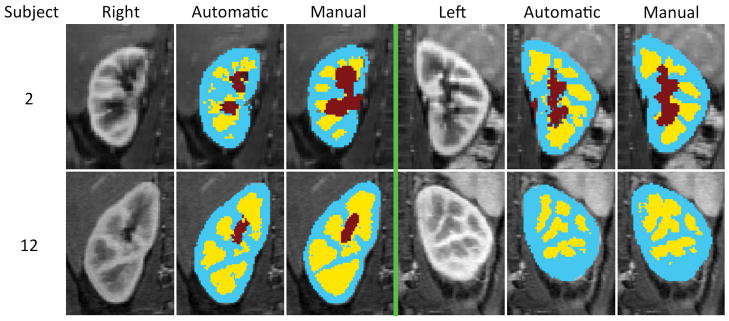
Some examples of the automated renal segmentation are shown in Fig. 7 and additional examples can be seen in Supporting Figure S1. The performance of the automatic segmentation for each subject can be seen in Table 1. All subjects considered, the automatic renal segmentation method had a mean precision of 0.95±0.006, a mean recall of 0.92±0.020, and a mean F1 score of 0.93±0.012 on the whole kidney. On the renal cortex maps, a mean precision of 0.85±0.011, a mean recall of 0.88±0.012 and a mean F1 score of 0.86±0.006 were observed. Over all 45 kidneys, mean (± standard error) kidney volume was 113±11.6 mL and mean cortical volume was 71±6.6 mL both obtained from manually drawn segmentation maps. Using the random forest classifier, mean volumetric estimation error and its standard error in renal cortex was 9.63±1.7 mL. The random forest classifier showed similar performance to the SVM classifier with radial basis functions and better performance compared to the AdaBoost classifier with decision trees. In the small dataset of 10,000 randomly chosen voxels, random forest classifier had an F1-score of 0.88 (precision=0.85, recall=0.91), the SVM classifier had an F1-score of 0.87 (precision=0.85, recall=0.90), and the AdaBoost had an F1-score of 0.85 (precision=0.82, recall=0.88).
FIG. 7.
The automatic segmentation results of two subjects. On each half, the leftmost column is a selected temporal phase of the DCE-MRI image, the middle column is the output of the automatic segmentation algorithm and the rightmost column is the manual segmentation map (i.e. ground truth). Extended version of this graph can be seen in Supporting Figure S1.
Table 1.
Segmentation and pharmacokinetic analysis results comparison between automatic and manual segmentation methods.
| Subject | Precision | Recall | F1 | GFRauto (ml/min) | GFRman (ml/min) | GFRerr (%) | Splitauto | Splitman | |
|---|---|---|---|---|---|---|---|---|---|
| Group 1 | 1 | 0.94 | 0.99 | 0.96 | 25.8 | 25.9 | 0.39 | 1.00 | 1.00 |
| 2 | 0.97 | 0.98 | 0.97 | 57.8 | 57.6 | 0.35 | 0.40 | 0.40 | |
| 3 | 0.92 | 0.99 | 0.95 | 16.6 | 17.4 | 4.60 | 0.50 | 0.50 | |
| 4 | 0.98 | 0.95 | 0.96 | 23.0 | 23.0 | 0.00 | 0.33 | 0.36 | |
| 5 | 0.97 | 0.95 | 0.96 | 38.6 | 39.1 | 1.28 | 1.00 | 1.00 | |
| 6 | 0.93 | 0.99 | 0.96 | 81.0 | 79.8 | 1.50 | 0.46 | 0.46 | |
| 7 | 0.92 | 0.98 | 0.95 | 29.2 | 28.7 | 1.74 | 0.28 | 0.28 | |
| 8 | 0.90 | 1.00 | 0.94 | 35.5 | 35.1 | 1.14 | 0.00 | 0.00 | |
| 9 | 0.92 | 0.96 | 0.94 | 91.8 | 90.0 | 2.00 | 0.52 | 0.53 | |
| 10 | 0.92 | 1.00 | 0.96 | 150.1 | 147.1 | 2.04 | 0.46 | 0.46 | |
| 11 | 0.92 | 0.99 | 0.96 | 36.6 | 36.1 | 1.39 | 1.00 | 1.00 | |
| Group 2 | 12 | 0.98 | 0.93 | 0.96 | 49.4 | 52.8 | 6.44 | 0.57 | 0.56 |
| 13 | 0.96 | 0.97 | 0.96 | 48.3 | 48.7 | 0.82 | 1.00 | 1.00 | |
| 14 | 0.88 | 0.51 | 0.64 | 30.6 | 37.0 | 17.30 | 1.00 | 0.80 | |
| 15 | 0.95 | 0.89 | 0.92 | 56.1 | 57.7 | 2.77 | 0.54 | 0.54 | |
| 16 | 0.94 | 0.94 | 0.94 | 38.7 | 38.2 | 1.31 | 0.37 | 0.37 | |
| 17 | 0.98 | 0.91 | 0.94 | 27.5 | 28.2 | 2.48 | 0.44 | 0.44 | |
| 18 | 0.98 | 0.94 | 0.90 | 18.6 | 19.7 | 5.58 | 0.00 | 0.02 | |
| 19 | 0.96 | 0.94 | 0.95 | 40.2 | 40.7 | 1.23 | 0.41 | 0.41 | |
| 20 | 0.90 | 0.81 | 0.85 | 38.1 | 39.0 | 2.31 | 0.40 | 0.38 | |
| 21 | 1.00 | 0.86 | 0.92 | 84.8 | 88.1 | 3.75 | 0.00 | 0.00 | |
| 22 | 0.98 | 0.86 | 0.91 | 80.1 | 84.2 | 4.87 | 0.47 | 0.50 | |
| Group 3 | 23 | 0.98 | 0.86 | 0.92 | 11.4 | 12.0 | 5.00 | 0.37 | 0.35 |
| 24 | 0.94 | 0.83 | 0.88 | 41.4 | 42.1 | 1.66 | 0.70 | 0.69 | |
| 25 | 0.97 | 0.90 | 0.93 | 53.9 | 55.7 | 3.23 | 0.70 | 0.70 | |
| 26 | 0.90 | 0.94 | 0.92 | 17.9 | 17.5 | 2.29 | 0.75 | 0.75 | |
| Average | Group 1 | 0.94 | 0.98 | 0.96 | 53.27 | 52.71 | 1.49 | 0.54 | 0.54 |
| Group 2 | 0.96 | 0.87 | 0.90 | 46.58 | 48.57 | 4.44 | 0.47 | 0.46 | |
| Group 3 | 0.95 | 0.88 | 0.91 | 31.15 | 31.83 | 3.05 | 0.63 | 0.62 | |
| All | 0.95 | 0.92 | 0.93 | 47.04 | 47.75 | 2.98 | 0.53 | 0.52 |
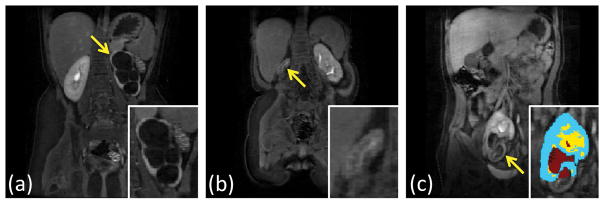
In subjects 14 and 18, the algorithm failed to detect one of the kidneys completely. One of the kidneys missed, the left kidney of subject 14, was relatively large (total kidney volume = 134 mL) due to hydronephrosis and did not show detectable medullary enhancement (Fig. 8a). In the other failed case, the right kidney of subject 18 was very small (total kidney volume = 3 mL) and did not show detectable medullary enhancement either (Fig. 8b). Another interesting case where the algorithm detected a kidney but failed to segment some parts was the right kidney of subject 20 (Fig. 8c). In this case, the section that was missed did not show significant medullary enhancement, and the kidney was in an unusual location in the pelvis.
FIG. 8.
Some examples of the failed segmentation cases. Arrows point to the kidneys the algorithm could not properly segment. (a) Subject 14 left kidney during excretory phase do not have visible medulla. (b) Subject 18 right kidney is too small to observe any structure. The coronal slice with the largest right kidney cross-section is shown in the figure. (c) Subject 20 right kidney during excretory phase does not have contrast accumulation in the lower half.
Pharmacokinetic Analysis
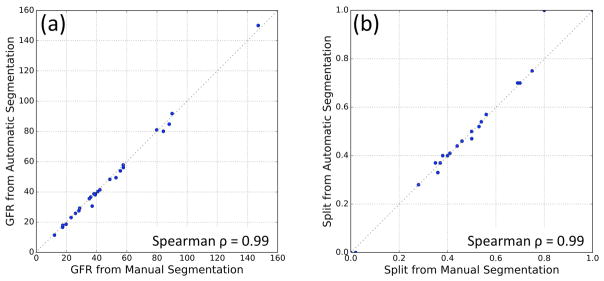
Single-kidney GFR estimations using the automatic method, GFRauto, and the manual method, GFRman, are compared in Fig. 9a. These two sets had a Spearman’s rank correlation coefficient ρ=0.99 (p<0.001). Mean absolute GFR estimation error of the automatic method was 2.98±0.66%. Right kidney split function calculated from GFRauto and GFRman were compared in Fig. 9b. Spearman’s ρ=0.99 (p<0.001) was observed in the split function measurements.
FIG. 9.
(a) Comparison of total GFR values obtained from manual segmentation maps vs automatic segmentation for all 26 subjects. (b) Right kidney split function comparison of the automatic and manual methods for all 26 subjects.
In the subjects where automatic segmentation failed to detect one of the kidneys, right kidney split functions calculated from automatic and manual segmentation maps were 1.00 (auto) and 0.80 (manual) for subject 14, and 0.00 (auto) and 0.02 (manual) for subject 18 (Table 1). These two subjects also had the highest skew in the manual split function compared to all other subjects with two kidneys.
Cortical Thickness Parameter
The results of the robustness test on the cortical thickness parameter (dctx) are shown in Supporting Figure S2. The segmentation performance was not sensitive to the choice of cortical thickness between 5 mm and 11 mm. However, the algorithm starts to break down when dctx drops below 5 mm due to low recall (i.e. missing some parts of the kidneys). Setting dctx above 11 mm caused low precision (i.e. more false positives) in the automatic segmentation maps.
Processing Time
Average processing time to obtain the renal parenchyma masks using the computer vision algorithm was 42 seconds per patient. The classification of the voxels using the support vector machine took an additional 3 seconds per patient on average. The expected run time of the full algorithm to obtain cortex, medulla and collecting system masks was 45 seconds/patient.
DISCUSSION
The results show that whole-kidney segmentation maps generated automatically are similar to the manually drawn counterparts in terms of both coverage (i.e. high sensitivity and precision) and GFR estimates. Segmentation of renal cortex on the other hand shows higher discrepancy between automatic and manual methods both in terms of volume and coverage. Visual inspection of the segmentation maps shows that higher discrepancy was caused by mislabeling in the cortex medulla interface. This is an expected result due to partial volume effects in the MR images. The cortical volume discrepancy between the SVM labeling and the ground truth labeling across all kidneys was 9.66±1.7 mL. This result was considered acceptable since the cortical volume discrepancy between the labeling of two human experts was reported as 16.3 mL in a previous study (33). Although the average renal cortex value was not reported in (33), if we assume a typical adult kidney volume of 178 mL (41) and a cortex-to-total volume ratio similar to our subjects (71 mL / 113 mL), we can estimate the average adult renal cortex volume of 112 mL. Under these assumptions, percent cortical volume discrepancy between two human experts in (33) can be estimated as 15% (16.3 mL / 112 mL). This value is very similar to the percent cortical volume discrepancy of 14% (9.66 mL / 71 mL) observed in our automatic segmentation method.
The automatic segmentation method proposed in this paper achieved comparable segmentation results to some of the published methods. Cuingned et al. (24) have demonstrated a fully automatic segmentation method for renal segmentation of CT images from 89 subjects. The authors report 80% success rate (Dice > 0.90) and 6% failure rate (Dice < 0.65) using dice coefficient (same as F1-score) as a metric. Using the same criteria, our algorithm achieves 88% success rate and 4% failure rate. The advantage of our method was the use of both spatial and temporal features as opposed to using the spatial features only. Tang et al. (32) proposed a fully automatic segmentation algorithm based on the analysis of MRI time-intensity curves using PCA and demonstrated the application in a pediatric subject. The cortical segmentation performance was reported using the arithmetic mean of recall and precision as 0.66 for one kidney and 0.71 for the other kidney. Our average cortical segmentation performance using the same arithmetic mean was 0.87 over all kidneys. Another MR renography segmentation method using a semi-automatic segmentation technique based on graph cuts was proposed by Rusinek et al. (23). The algorithm requires manual intervention to select seed regions in the renal cortex and medulla. The average GFR estimation discrepancy over 22 clinical datasets was reported as 13.5% and the segmentation time was 20 minutes per kidney. In our application, the GFR estimation error was 2.98% over 26 clinical datasets. However, the pharmacokinetic models used in these studies were different and the discrepancy cannot be attributed solely to the segmentation performance. In addition, our sample size of 26 subjects is limited and a bigger study with more subjects is needed to evaluate the actual clinical performance of our algorithm. We are currently working on acquiring more datasets by deploying the automatic segmentation algorithm to our hospital.
The single-kidney and total-GFR estimates in this study were obtained by performing 2-compartment analysis on the full-kidney segmentation maps. Some compartmental models used for GFR estimation need ROIs of both cortex and medulla whereas some models only require the ROIs of either cortex or the whole kidney (42). Although our algorithm performs on par with the experts for cortical segmentation, use of the cortical ROIs with the 2-compartment model is not desirable as the model depends on the ROI volume directly. In our study, the average cortical volume was 71.1 mL. A discrepancy of 9.66 mL in the cortex medulla interface, where the tissues are contributing to the filtration, could potentially cause a GFR estimation error of 14%. For this reason, we decided to use the whole-kidney ROI in our GFR analysis instead of the renal cortex ROIs. A similar approach was taken by Tofts et al. (10) by including renal parenchyma in the analysis. They showed that as the size of the cortical ROI grows to include the whole kidney, the GFR estimates also grow up until a point and then reach a plateau once the ROIs fully include the renal parenchyma. This means using an ROI that does not fully include the renal parenchyma may underestimate the GFR, however, selecting a larger ROI does not cause overestimation. In addition, using a large ROI enables us to include more time points (90s) in our analysis because the 2-compartment model assumes that the contrast never leaves the ROI (10).
Some of the parameters used in automatic segmentation, such as the radius of the neighborhood for grouping medulla clusters and expanding them to cover the cortex, were based on the maximum cortical thickness of 11mm reported in (35). In order for this algorithm to work, the actual cortical thickness should not exceed 11 mm and medulla clusters should be within 11 mm edge-to-edge distance from each other. Supporting Figure S2 shows the automatic segmentation performance under different assumed cortical thickness (dctx) values. When the cortical thickness parameter is below 5 mm, there is a significant drop in the automatic segmentation performance as our assumption of the actual cortical thickness being less than the cortical thickness parameter (dctx) is no longer true. In addition to these spatial constraints, the kidneys have to be functioning for the automatic segmentation as the initial detection of medulla regions rely on the accumulation of the contrast agent in the tissues. The GrabCut segmentation also depends on functional enhancement of the renal tissues as the unique signal-time curves of the renal voxels are mapped on to the color space through PCA.
In the case of anatomical anomalies, where the medulla clusters are more than one cortical thickness apart, the algorithm may fail to label the kidneys correctly. Hence, a visual inspection of the segmentation maps by a radiologist or a trained post-processing technologist is required to identify the failed segmentations. There are three possible reasons for the automatic segmentation to fail. The first one is failing to detect the bounding box around a kidney automatically. These failed cases may be segmented again by running the GrabCut algorithm using a manually drawn bounding box of the problematic kidney. This is still faster than full manual segmentation because the operator has to define only a loose bounding box. The second possible reason for a segmentation to fail is that some parts of the kidney look very similar to the background under PCA mapping (i.e. the signal-time curves are more like non-kidney tissues). These cases require the operator to manually identify the seed regions for a graph cut segmentation. The user-assisted GrabCut segmentation is described in (37) and the amount of manual work should be less than using a standard graph cut technique (23). The third reason is if there is very little or no filtration in the kidneys and the PCA fails to map renal tissues to unique colors. Segmentation of these cases is difficult and manual segmentation may be required. However, if the main goal is to measure the GFR, these non-functional kidneys do not contribute to the GFR as much as the functioning kidney and the estimation error due to missing the non-functional kidney would be very low. An example of this can be seen in Fig. 8. Table 1 shows the recall performance of the automated segmentation of subject 14 (Fig. 8a) as 0.51, meaning almost half of the true kidney labels are missed (because the left kidney was not detected.) However, the GFR estimation error on this subject is only 17.30% (Table 1). The automated algorithm missed this kidney because it did not show much enhancement in the medulla or collecting system.
The proposed segmentation method may be used on datasets acquired using different protocols however additional preprocessing steps, such as image registration may be required. We have demonstrated the technique on three different datasets. The datasets from group 1 were acquired using VDRad with a fast bolus injection (1 mL/s). The group 2 datasets were also acquired using VDRad but with a slow bolus injection (0.3 mL/s). The group 3 datasets were acquired using DISCO with a slow bolus injection (0.3 mL/s). Image registration was not performed in this study as the reconstructions from groups 1 and 2 were soft-gated for respiratory motion using butterfly navigation data and no apparent motion was observed between different temporal frames. Similarly, group 3 acquisitions were respiratory-triggered and no apparent motion of the kidneys was observed.
The automatic detection of renal bounding boxes is application specific. However, the GrabCut algorithm with PCA mapping can be used for segmentation of time-resolved medical images outside the renal application. Similarly, the machine learning approach to classify voxels can be adapted to other areas like detection of tumors based on the temporal features. The source code of the automatic segmentation algorithm is publicly available on GitHub (https://github.com/umityoruk/renal-segmentation.git).
During the development of the algorithm, we tried to perform full renal segmentation by classifying voxels using only temporal features. An SVM was trained to perform a binary classification, kidney vs. other, on each voxel of the DCE-MRI dataset. This approach failed to yield good segmentation maps due to high inter-subject variance in temporal features (i.e. signal-time curves may appear different between two subjects due to differences in contrast injection speed, heart rate, age, etc.). Alternatively, we tried to locate the kidneys in the abdominal space by first detecting the renal cortex. This task proved challenging for certain datasets where the cortical enhancement looked very similar to the neighboring tissues such as liver and spleen (Supporting Figure S3). Hence, we decided to target medullary voxels where the signal continues to increase between 30 and 90 seconds following the contrast arrival. The advantage of our current approach is that we mainly constrained our scoring to the amount of contrast accumulation in a voxel, which is expected in medulla and the collecting system, and defined a new threshold for each subject (Otsu’s threshold) instead of using a single global cut-off for all subjects. Any signal delays or intensity differences between subjects do not affect the classification. The PCA mapping before the GrabCut segmentation is also trained and applied on each subject individually instead of training using the whole dataset. Since PCA maximizes the variance in the projected space, the voxels with different time-intensity curves appear different in color no matter what other subjects’ time-intensity curves look like, making the GrabCut segmentation easier. Hence, the proposed algorithm is more robust to inter-subject differences than just using an SVM.
In conclusion, we have developed a new technique to automatically segment kidneys from the DCE-MRI data using computer vision and machine learning. Specifically, we have developed a heuristic approach to locating kidneys using the medulla as a target (i.e. medulla score map), modified the GrabCut algorithm to work in 3D, applied the GrabCut algorithm to the time resolved MRI data using PCA dimensionality reduction, and trained a random forest classifier for renal cortex segmentation. We have used this new technique with a 2-compartment model to estimate GFR in pediatric patients and showed that the results are nearly identical to the GFR estimates obtained using a manual segmentation technique while reducing the segmentation time from several hours to 45 seconds per patient.
Supplementary Material
Supporting Figure S1. The automatic segmentation results of five subjects. On each half the leftmost column is a selected temporal phase of the DCE-MRI image, the middle column is the output of the automatic segmentation algorithm and the rightmost column is the manual segmentation map (i.e. ground truth). Subjects 2 and 9 are from Group 1, 12 and 19 are from Group 2, and 25 is from Group 3.
Supporting Figure S2. Automatic segmentation performance with various cortical thickness (dctx) assumptions. The error bars show the standard error. The segmentation performance was not affected by the cortical thickness parameters between 5 mm and 11 mm.
Supporting Figure S3. Locating renal cortex from intensity images can be difficult. The left image is taken from Subject 4 at 45s after the initial enhancement of the renal cortex. Notice the interface between the liver and the renal cortex. These two tissues are hard to distinguish based on the intensity level alone. The image on the right, taken from Subject 3 at 6s after the initial enhancement, has a cortical enhancement non-distinguishable from the splenic tissue. In both of these cases relying on the intensity of the cortical voxels prevent successful segmentation. Since the renal cortex does not always stand out as it does in some pristine datasets, we have decided to evaluate voxels based on their intensity-time curves. We targeted the medullary voxels, which have distinctly shaped signal time curves as seen in Fig. 2.
Contributor Information
Umit Yoruk, Stanford University.
Brian A. Hargreaves, Stanford University
Shreyas S. Vasanawala, Stanford University
References
- 1.Coresh J, Selvin E, Stevens LA, Manzi J, Kusek JW, Eggers P, Van Lente F, Levey AS. Prevalence of chronic kidney disease in the United States. Jama. 2007;298(17):2038–2047. doi: 10.1001/jama.298.17.2038. [DOI] [PubMed] [Google Scholar]
- 2.Whyte DA, Fine RN. Chronic Kidney Disease in Children. Pediatrics in Review. 2008 Oct;29(10):335–341. doi: 10.1542/pir.29-10-335. [DOI] [PubMed] [Google Scholar]
- 3.Warady BA, Chadha V. Chronic kidney disease in children: the global perspective. Pediatric Nephrology. 2007 Nov;22(12):1999–2009. doi: 10.1007/s00467-006-0410-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jones RA, Easley K, Little SB, Scherz H, Kirsch AJ, Grattan-Smith JD. Dynamic Contrast-Enhanced MR Urography in the Evaluation of Pediatric Hydronephrosis: Part 1, Functional Assessment. American Journal of Roentgenology. 2005 Dec;185(6):1598–1607. doi: 10.2214/AJR.04.1540. [DOI] [PubMed] [Google Scholar]
- 5.Jones RA, Perez-Brayfield MR, Kirsch AJ, Grattan-Smith JD. Renal Transit Time with MR Urography in Children1. Radiology. 2004 Oct;233(1):41–50. doi: 10.1148/radiol.2331031117. [DOI] [PubMed] [Google Scholar]
- 6.Rohrschneider WK, Haufe S, Wiesel M, Tönshoff B, Wunsch R, Darge K, Clorius JH, Tröger J. Functional and Morphologic Evaluation of Congenital Urinary Tract Dilatation by Using Combined Static-Dynamic MR Urography: Findings in Kidneys with a Single Collecting System1. Radiology. 2002 Sep;224(3):683–694. doi: 10.1148/radiol.2243011207. [DOI] [PubMed] [Google Scholar]
- 7.Annet L, Hermoye L, Peeters F, Jamar F, Dehoux J-P, Van Beers BE. Glomerular filtration rate: Assessment with dynamic contrast-enhanced MRI and a cortical-compartment model in the rabbit kidney. Journal of Magnetic Resonance Imaging. 2004 Nov;20(5):843–849. doi: 10.1002/jmri.20173. [DOI] [PubMed] [Google Scholar]
- 8.Hackstein N, Heckrodt J, Rau WS. Measurement of single-kidney glomerular filtration rate using a contrast-enhanced dynamic gradient-echo sequence and the Rutland-Patlak plot technique. Journal of Magnetic Resonance Imaging. 2003 Dec;18(6):714–725. doi: 10.1002/jmri.10410. [DOI] [PubMed] [Google Scholar]
- 9.Lee VS, Rusinek H, Bokacheva L, Huang AJ, Oesingmann N, Chen Q, Kaur M, Prince K, Song T, Kramer EL, Leonard EF. Renal function measurements from MR renography and a simplified multicompartmental model. AJP: Renal Physiology. 2007 Jan;292(5):F1548–F1559. doi: 10.1152/ajprenal.00347.2006. [DOI] [PubMed] [Google Scholar]
- 10.Tofts PS, Cutajar M, Mendichovszky IA, Peters AM, Gordon I. Precise measurement of renal filtration and vascular parameters using a two-compartment model for dynamic contrast-enhanced MRI of the kidney gives realistic normal values. European Radiology. 2012 Jun;22(6):1320–1330. doi: 10.1007/s00330-012-2382-9. [DOI] [PubMed] [Google Scholar]
- 11.Henderson E, Rutt BK, Lee TY. Temporal sampling requirements for the tracer kinetics modeling of breast disease. Magnetic resonance imaging. 1998;16(9):1057–1073. doi: 10.1016/s0730-725x(98)00130-1. [DOI] [PubMed] [Google Scholar]
- 12.Chandarana H, Block TK, Rosenkrantz AB, Lim RP, Kim D, Mossa DJ, Babb JS, Kiefer B, Lee VS. Free-breathing radial 3D fat-suppressed T1-weighted gradient echo sequence: a viable alternative for contrast-enhanced liver imaging in patients unable to suspend respiration. Investigative radiology. 2011;46(10):648–653. doi: 10.1097/RLI.0b013e31821eea45. [DOI] [PubMed] [Google Scholar]
- 13.Cheng JY, Zhang T, Ruangwattanapaisarn N, Alley MT, Uecker M, Pauly JM, Lustig M, Vasanawala SS. Free-breathing pediatric MRI with nonrigid motion correction and acceleration: Free-Breathing Pediatric MRI. Journal of Magnetic Resonance Imaging. 2014 Oct; doi: 10.1002/jmri.24785. n/a–n/a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lim RP, Shapiro M, Wang EY, Law M, Babb JS, Rueff LE, Jacob JS, Kim S, Carson RH, Mulholland TP, Laub G, Hecht EM. 3D Time-Resolved MR Angiography (MRA) of the Carotid Arteries with Time-Resolved Imaging with Stochastic Trajectories: Comparison with 3D Contrast-Enhanced Bolus-Chase MRA and 3D Time-Of-Flight MRA. American Journal of Neuroradiology. 2008 Sep;29(10):1847–1854. doi: 10.3174/ajnr.A1252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Michaely HJ, Morelli JN, Budjan J, Riffel P, Nickel D, Kroeker R, Schoenberg SO, Attenberger UI. CAIPIRINHA-Dixon-TWIST (CDT)-volume-interpolated breath-hold examination (VIBE): a new technique for fast time-resolved dynamic 3-dimensional imaging of the abdomen with high spatial resolution. Investigative radiology. 2013;48(8):590–597. doi: 10.1097/RLI.0b013e318289a70b. [DOI] [PubMed] [Google Scholar]
- 16.Saranathan M, Rettmann DW, Hargreaves BA, Clarke SE, Vasanawala SS. DIfferential subsampling with cartesian ordering (DISCO): A high spatio-temporal resolution dixon imaging sequence for multiphasic contrast enhanced abdominal imaging. Journal of Magnetic Resonance Imaging. 2012 Jun;35(6):1484–1492. doi: 10.1002/jmri.23602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Xu B, Spincemaille P, Chen G, Agrawal M, Nguyen TD, Prince MR, Wang Y. Fast 3D contrast enhanced MRI of the liver using temporal resolution acceleration with constrained evolution reconstruction. Magnetic Resonance in Medicine. 2013 Feb;69(2):370–381. doi: 10.1002/mrm.24253. [DOI] [PubMed] [Google Scholar]
- 18.Feng L, et al. Golden-angle radial sparse parallel MRI: Combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI: iGRASP: Iterative Golden-Angle RAdial Sparse Parallel MRI. Magnetic Resonance in Medicine. 2014 Sep;72(3):707–717. doi: 10.1002/mrm.24980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Song T, Laine AF, Chen Q, Rusinek H, Bokacheva L, Lim RP, Laub G, Kroeker R, Lee VS. Optimal k-space sampling for dynamic contrast-enhanced MRI with an application to MR renography. Magnetic Resonance in Medicine. 2009 May;61(5):1242–1248. doi: 10.1002/mrm.21901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yoruk U, Saranathan M, Loening AM, Hargreaves BA, Vasanawala SS. High temporal resolution dynamic MRI and arterial input function for assessment of GFR in pediatric subjects: HTR DCE MRI and AIF for GFR Assessment. Magnetic Resonance in Medicine. 2016 Mar;75(3):1301–1311. doi: 10.1002/mrm.25731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pandey A, Yoruk U, Keerthivasan M, Galons JP, Sharma P, Johnson K, Martin DR, Altbach M, Bilgin A, Saranathan M. Multiresolution imaging using golden angle stack-of-stars and compressed sensing for dynamic MR urography: Multiresolution Imaging for Dynamic MR Urography. Journal of Magnetic Resonance Imaging. 2017 Feb; doi: 10.1002/jmri.25576. [DOI] [PubMed] [Google Scholar]
- 22.Zhang T, Cheng JY, Potnick AG, Barth RA, Alley MT, Uecker M, Lustig M, Pauly JM, Vasanawala SS. Fast pediatric 3D free-breathing abdominal dynamic contrast enhanced MRI with high spatiotemporal resolution: Pediatric Free-Breathing Abdominal DCE MRI. Journal of Magnetic Resonance Imaging. 2013 Dec; doi: 10.1002/jmri.24551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rusinek H, Boykov Y, Kaur M, Wong S, Bokacheva L, Sajous JB, Huang AJ, Heller S, Lee VS. Performance of an automated segmentation algorithm for 3D MR renography. Magnetic Resonance in Medicine. 2007 Jun;57(6):1159–1167. doi: 10.1002/mrm.21240. [DOI] [PubMed] [Google Scholar]
- 24.Cuingnet R, Prevost R, Lesage D, Cohen LD, Mory B, Ardon R. Automatic detection and segmentation of kidneys in 3D CT images using random forests. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2012; Springer; 2012. pp. 66–74. [DOI] [PubMed] [Google Scholar]
- 25.Li Xiuli, Chen Xinjian, Yao Jianhua, Zhang Xing, Yang Fei, Tian Jian. Automatic Renal Cortex Segmentation Using Implicit Shape Registration and Novel Multiple Surfaces Graph Search. IEEE Transactions on Medical Imaging. 2012 Oct;31(10):1849–1860. doi: 10.1109/TMI.2012.2203922. [DOI] [PubMed] [Google Scholar]
- 26.Yuksel SE, El-Baz A, Farag AA, Abo El-Ghar ME, Eldiasty TA, Ghoneim MA. Automatic detection of renal rejection after kidney transplantation. International Congress Series. 2005 May;1281:773–778. [Google Scholar]
- 27.Boykov Y, Lee VS, Rusinek H, Bansal R. Segmentation of dynamic ND data sets via graph cuts using Markov models,” in. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2001. 2001:1058–1066. [Google Scholar]
- 28.de Priester JA, Kessels AG, Giele EL, den Boer JA, Christiaans MH, Hasman A, van Engelshoven J. MR renography by semiautomated image analysis: performance in renal transplant recipients. Journal of Magnetic Resonance Imaging. 2001;14(2):134–140. doi: 10.1002/jmri.1163. [DOI] [PubMed] [Google Scholar]
- 29.Sun Y, Jolly M-P, Moura JM. Integrated registration of dynamic renal perfusion MR images. Image Processing, 2004. ICIP’04. 2004 International Conference on; 2004; pp. 1923–1926. [Google Scholar]
- 30.Sun Y, Moura JM, Yang D, Ye Q, Ho C. Kidney segmentation in MRI sequences using temporal dynamics. Biomedical Imaging, 2002. Proceedings. 2002 IEEE International Symposium on; 2002; pp. 98–101. [Google Scholar]
- 31.Zöllner FG, Sance R, Rogelj P, Ledesma-Carbayo MJ, Rørvik J, Santos A, Lundervold A. Assessment of 3D DCE-MRI of the kidneys using non-rigid image registration and segmentation of voxel time courses. Computerized Medical Imaging and Graphics. 2009 Apr;33(3):171–181. doi: 10.1016/j.compmedimag.2008.11.004. [DOI] [PubMed] [Google Scholar]
- 32.Tang Y, Jackson HA, De Filippo RE, Nelson MD, Moats RA. Automatic renal segmentation applied in pediatric MR Urography. International Journal of Intelligent Information Processing. 2010 Sep;1(1):12–19. [Google Scholar]
- 33.Song T, Lee VS, Rusinek H, Bokacheva L, Laine A. Segmentation of 4D MR renography images using temporal dynamics in a level set framework. Biomedical Imaging: From Nano to Macro, 2008. ISBI 2008. 5th IEEE International Symposium on; 2008; pp. 37–40. [Google Scholar]
- 34.Song T, Lee VS, Rusinek H, Wong S, Laine AF. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2006. Springer; 2006. Integrated four dimensional registration and segmentation of dynamic renal MR images; pp. 758–765. [DOI] [PubMed] [Google Scholar]
- 35.Beland MD, Walle NL, Machan JT, Cronan JJ. Renal Cortical Thickness Measured at Ultrasound: Is It Better Than Renal Length as an Indicator of Renal Function in Chronic Kidney Disease? American Journal of Roentgenology. 2010 Aug;195(2):W146–W149. doi: 10.2214/AJR.09.4104. [DOI] [PubMed] [Google Scholar]
- 36.Otsu N. A threshold selection method from gray-level histograms. Automatica. 1975;11(285–296):23–27. [Google Scholar]
- 37.Rother C, Kolmogorov V, Blake A. Grabcut: Interactive foreground extraction using iterated graph cuts,” in. ACM transactions on graphics (TOG) 2004;23:309–314. [Google Scholar]
- 38.Boykov YY, Jolly MP. Interactive graph cuts for optimal boundary & region segmentation of objects in ND images. International Conference of Computer vision; 2001. pp. 105–112. [Google Scholar]
- 39.Sasaki M, Shibata E, Kanbara Y, Ehara S. Enhancement effects and relaxivities of gadolinium-DTPA at 1.5 versus 3 Tesla: a phantom study. Magn Reson Med Sci. 2005;4(3):145–149. doi: 10.2463/mrms.4.145. [DOI] [PubMed] [Google Scholar]
- 40.Stanisz GJ, et al. T1, T2 relaxation and magnetization transfer in tissue at 3T. Magnetic Resonance in Medicine. 2005 Sep;54(3):507–512. doi: 10.1002/mrm.20605. [DOI] [PubMed] [Google Scholar]
- 41.Cheong B, Muthupillai R, Rubin MF, Flamm SD. Normal Values for Renal Length and Volume as Measured by Magnetic Resonance Imaging. Clinical Journal of the American Society of Nephrology. 2006 Nov;2(1):38–45. doi: 10.2215/CJN.00930306. [DOI] [PubMed] [Google Scholar]
- 42.Bokacheva L, Rusinek H, Zhang JL, Chen Q, Lee VS. Estimates of glomerular filtration rate from MR renography and tracer kinetic models. Journal of Magnetic Resonance Imaging. 2009 Feb;29(2):371–382. doi: 10.1002/jmri.21642. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Figure S1. The automatic segmentation results of five subjects. On each half the leftmost column is a selected temporal phase of the DCE-MRI image, the middle column is the output of the automatic segmentation algorithm and the rightmost column is the manual segmentation map (i.e. ground truth). Subjects 2 and 9 are from Group 1, 12 and 19 are from Group 2, and 25 is from Group 3.
Supporting Figure S2. Automatic segmentation performance with various cortical thickness (dctx) assumptions. The error bars show the standard error. The segmentation performance was not affected by the cortical thickness parameters between 5 mm and 11 mm.
Supporting Figure S3. Locating renal cortex from intensity images can be difficult. The left image is taken from Subject 4 at 45s after the initial enhancement of the renal cortex. Notice the interface between the liver and the renal cortex. These two tissues are hard to distinguish based on the intensity level alone. The image on the right, taken from Subject 3 at 6s after the initial enhancement, has a cortical enhancement non-distinguishable from the splenic tissue. In both of these cases relying on the intensity of the cortical voxels prevent successful segmentation. Since the renal cortex does not always stand out as it does in some pristine datasets, we have decided to evaluate voxels based on their intensity-time curves. We targeted the medullary voxels, which have distinctly shaped signal time curves as seen in Fig. 2.