Prediction of New Stabilizing Mutations Based on Mechanistic Insights from Markov State Models

Abstract

Protein stabilization is fundamental to enzyme function and evolution, yet understanding the determinants of a protein’s stability remains a challenge. This is largely due to a shortage of atomically detailed models for the ensemble of relevant protein conformations and their relative populations. For example, the M182T substitution in TEM β-lactamase, an enzyme that confers antibiotic resistance to bacteria, is stabilizing but the precise mechanism remains unclear. Here, we employ Markov state models (MSMs) to uncover how M182T shifts the distribution of different structures that TEM adopts. We find that M182T stabilizes a helix that is a key component of a domain interface. We then predict the effects of other mutations, including a novel stabilizing mutation, and experimentally test our predictions using a combination of stability measurements, crystallography, NMR, and in vivo measurements of bacterial fitness. We expect our insights and methodology to provide a valuable foundation for protein design.

Short abstract

Markov state models guide experiments to determine the mechanism of stabilization for a clinical mutant of TEM-1 β-lactamase, which leads to the prediction of a new stabilizing mutant.

Introduction

Studying the evolution of antibiotic resistance has provided many insights into how proteins acquire new functions, but the mechanistic basis for how mutations alter a protein’s activity and stability often remains unclear. For example, studying how bacteria evolve variants of TEM β-lactamase that confer resistance to new antibiotics by degrading these drugs has revealed that many of the mutations that give rise to new functions are destabilizing. Therefore, it is common for proteins to acquire one or more mutations that alter their function and then to acquire additional mutations that restore stability.¹ M182T is one such stabilizing mutation in TEM, and it has appeared in numerous clinical isolates and directed evolution experiments.²⁻⁴ This substitution occurs far from the active site (Figure 1A) and, on its own, has little effect on TEM’s activity. It is often called a global suppressor because of its ability to counterbalance the destabilizing effects of a wide variety of other substitutions that do alter TEM’s activity.³ Despite over two decades of work on this variant, the mechanism of stabilization by M182T is not understood well enough to predict new stabilizing mutations. Elucidating the mechanism underlying this stabilization would provide a basis for predicting other global suppressors and eventually developing quantitative design principles.

Figure 1.

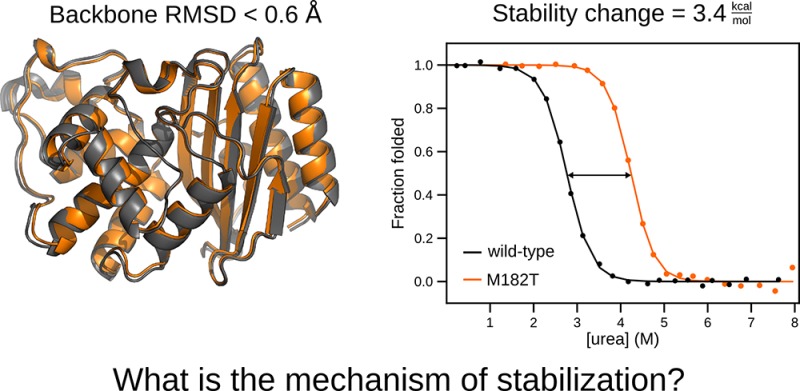
Representative structures of TEM that highlight two potential mechanisms for stabilization by Thr182. (A) Crystal structure of TEM with mutation M182T (PDB 1JWP). The backbone of the α-helix domain (cyan), β-sheet domain (gray), and s2h2 loop (orange) are represented as a cartoon. Active site residue, Ser70, and the stabilizing mutation, Thr182, are shown in sticks. (B) A representative structure of the first mechanism, observed in MD simulations, where Thr182 hydrogen-bonds to the s2h2 loop. (C) A representative structure of the second mechanism, observed in MD simulations, where Thr182 caps helix 9.

A mechanistic understanding of how M182T stabilizes TEM remains elusive because of a lack of methods that provide both a detailed structural model of the relevant species and their relative populations. Spectroscopic studies have revealed that TEM-1, which we will refer to as wild-type TEM, populates at least three states at equilibrium: a native state (N), an intermediate state (I), and an unfolded state (U).⁵ Introducing the M182T substitution appears to reduce the number of equilibrium states to two.⁴ However, there is debate over whether this results from M182T stabilizing the native state or destabilizing the intermediate.⁶ Moreover, these spectroscopic experiments do not directly provide a structural model for how M182T shifts the relative populations of these states. Two competing structural models based on crystallographic data have been proposed to explain M182T’s ability to stabilize the enzyme. In the first model, Thr182 is poised to form a hydrogen bond between TEM’s two structural domains, interacting with the backbone carbonyls of Glu63 and Glu64 in an adjacent loop⁷ (Figure 1B). Therefore, it was proposed that M182T stabilizes TEM by strengthening the interface between the α-helix and β-sheet domains. However, in a later structure, Thr182 is oriented to form hydrogen bonds with the backbone amide of Ala185 (Figure 1C).¹ Based on this model, it was proposed that M182T stabilizes the protein by forming a hydrogen bond between its side chain and an unfulfilled backbone donor at the end of helix 9 in a classic N-capping interaction. In all likelihood, both of these structures are present at thermal equilibrium, but it is impossible to conclude which, if either, of these interactions plays a dominant role in stabilizing TEM from the crystallographic data.

Here, we employ Markov state models (MSMs)⁸⁻¹⁰ to understand how M182T shifts the distribution of different structures that TEM adopts. These models provide a quantitative description of a protein’s thermodynamics and kinetics by defining its structural states and the rates of transitioning between them. We have previously compared MSMs of variants that alter TEM’s specificity to understand how they change the protein’s function.¹¹ In this study, we compare MSMs of the wild-type and M182T variants to infer how M182T stabilizes TEM. We then predict the effects of other mutations, including new global suppressor mutations, and experimentally test our predictions using a combination of spectroscopic measurements of protein stability, nuclear magnetic resonance (NMR) measurements of chemical shifts, a crystal structure, and in vivo measurements of the fitness of bacteria expressing our newly designed TEM variants.

Results and Discussion

M182T Stabilizes the Native State

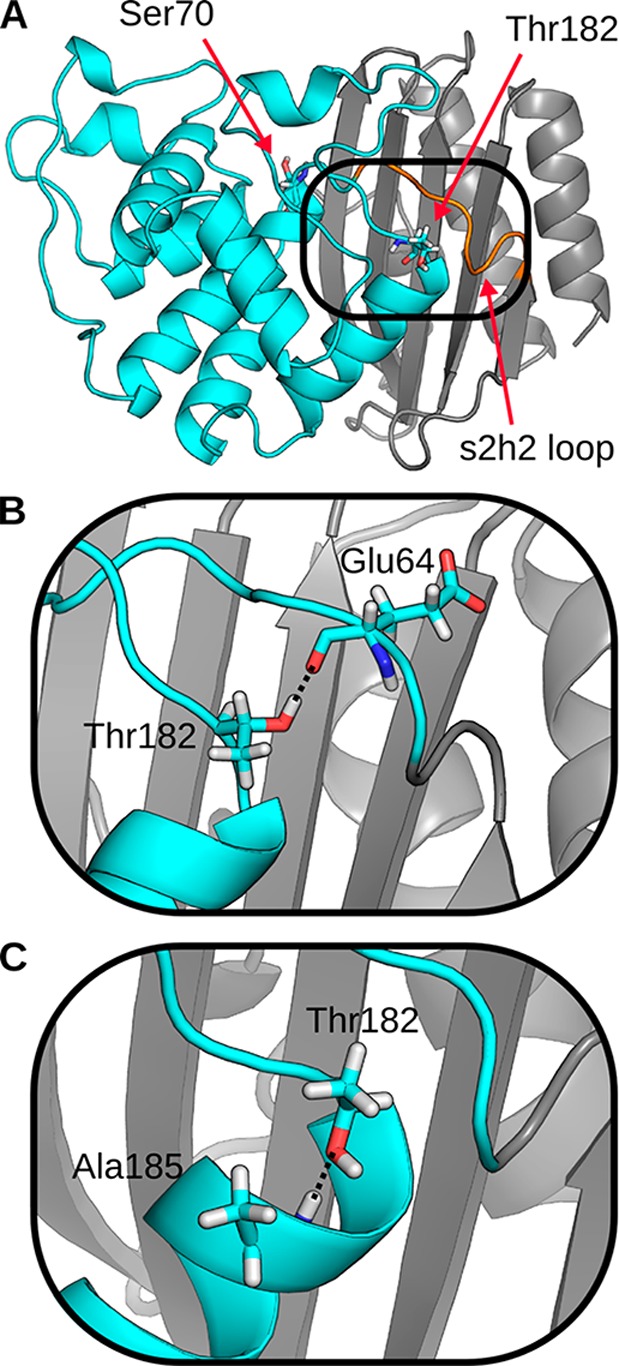
Uncertainty over whether M182T stabilizes the native state or destabilizes the intermediate stems from the limited ability of any one spectroscopic observable to clearly distinguish all three thermodynamic states. For example, circular dichroism (CD) fails to adequately capture M182T’s intermediate state. By CD, there are three distinguishable states for wild-type⁵ but only two for M182T⁴ (Figure 2A); however, the dependence of M182T’s native-state stability on denaturant, as reflected in its m value, is shallower than expected for a protein of its size.¹² This indicates that, like wild-type, M182T likely populates more than two states at equilibrium,¹³ rendering a two-state model insufficient. Fluorescence also fails to capture all three thermodynamic states for both wild-type and M182T (Figure 2B). Previous studies of β-lactamases have established that the intermediate state has the same fluorescence as the unfolded state,¹⁴ so fluorescence captures only the transition between the native and intermediate states.

Figure 2.

Chemical melts of TEM. Shown are the fractions of folded protein for wild-type TEM (black) and TEM M182T (orange) as a function of [urea]. (A) Monitoring circular dichroism signal. (B) Monitoring intrinsic fluorescence at 340 nm.

To overcome the limitations of a single spectroscopic observable, we performed global fits to the fluorescence and CD data for each variant, assuming that the first transition observed by CD is the same as that observed by fluorescence. Doing so allows us to disambiguate the two transitions captured by CD by leveraging the single transition captured by fluorescence. Our global fits reveal that M182T stabilizes the native state without destabilizing the intermediate. The free energy difference between the native and intermediate states of M182T is 3.3 kcal/mol greater than that for wild-type (Table 1). In contrast, the free energy differences between the intermediate and unfolded states are the same, within error, for both variants.

Table 1. Stabilities of TEM β-Lactamase Variants^a.

	ΔGun (kcal mol–1)	mun (kcal mol–1 M–1)	ΔGinb (kcal mol–1)	minb (kcal mol–1 M–1)	ΔGuib (kcal mol–1)	muic (kcal mol–1 M–1)
wild-type	14.3 ± 0.3	3.8 ± 0.2	6.0 ± 0.1	2.1 ± 0.1	8.3 ± 0.1	1.7 ± 0.1
M182T	17.7 ± 0.4	4.1 ± 0.2	10.0 ± 0.6	2.4 ± 0.2	7.8 ± 0.2	1.7, fixed
M182S	18.5 ± 0.5	4.4 ± 0.1	10.6 ± 0.5	2.7 ± 0.1	7.9 ± 0.4	1.7, fixed
M182V	13.5 ± 0.3	3.8 ± 0.1	5.4 ± 0.2	2.1 ± 0.1	8.2 ± 0.1	1.7, fixed
M182N	13.7 ± 0.5	3.8 ± 0.1	5.9 ± 0.4	2.1 ± 0.1	7.8 ± 0.4	1.7, fixed

^aAll measurements were repeated three times. Errors are standard deviations.

^bDetermined using a global fit of fluorescence data to a two-state (I–N) model and CD data to a three-state (U–I–N) model using the linear extrapolation method (see Methods).

^cThe value for m_ui was fixed to the average value determined for wild-type. The addition of m_ui as a parameter did not significantly improve the quality of the fit, as determined by F-tests (values in the range of 1 × 10^–10 to 1 × 10^–7, see Methods).

M182T Stabilizes Helix 9

Given our assumption that M182T does not affect the unfolded ensemble and, thus, primarily stabilizes the native state, we reason that it should be possible to infer the mechanism of stabilization from analysis of native-state ensembles. To accomplish this, we use MSMs to provide an atomically detailed representation of conformational heterogeneity in the native state that is currently unavailable to many experimental techniques. Doing so enables us to quantify the probabilities of various interactions in a manner that is not possible with the static structures from techniques like crystallography. Furthermore, by identifying interactions that are formed in M182T’s native-state ensemble but not that of wild-type TEM we can narrow down the secondary effects of this mutation.

To efficiently identify the interactions that Thr182 forms, we employed our FAST simulation method^15,16 to build MSMs of the wild-type and M182T variants of TEM. FAST is a goal-oriented adaptive sampling method in which we (1) run a batch of simulations, (2) build an MSM from all the simulation data collected so far, (3) rank each state with a function that favors states that optimize some geometric criteria, as well as a statistical criterion that favors poorly sampled states, (4) run a new batch of simulations from the highest ranked states, (5) repeat steps 2–4 for some number of iterations, and (6) build a final MSM from all the simulation data. For this study, we sought to maximize the RMSD from the starting structure to maximize the number of different structures identified by the final model. We have previously established that FAST captures rare events with orders of magnitude less simulation data than conventional molecular dynamics simulations.¹⁵ Therefore, the 6.5 μs of simulation data we collected for each variant should be sufficient to construct a quantitatively predictive map of the native-state ensemble.¹⁷

Analysis of our FAST simulations reveals that M182T prefers to act as an N-terminal capping residue to helix 9. This conclusion comes from quantifying the probabilities of all the different contacts Thr182’s side chain can form. Doing so reveals that Thr182 predominantly caps helix 9 by forming a hydrogen bond with Ala185 with a probability of 0.72 ± 0.02. Thr182 also forms a hydrogen bond with the backbone carbonyl of Glu64 with a probability of 0.12 ± 0.02. Thus, we observe both conformations captured in the two competing crystal structures. The probabilities of other contacts, such as the hydrogen bond with the backbone carbonyl of Glu63, are negligible.

While it is tempting to conclude that capping is sufficient for global stabilization, we instead propose that the stability of helix 9 is a better predictor of TEM’s stability. Our model’s distinction between capping and helix stability was motivated by the observation that other residues capable of N-capping have not been observed at position 182 either in clinical isolates or in directed evolution studies.² It might seem intuitive that capping would stabilize helix 9, but, in the next section, we defy this intuition by identifying a residue that caps without conferring global stabilization. Previous work on the folding of β-lactamases provides a foundation for our model by suggesting that the α-helix domain is largely folded in the intermediate state but the β-sheet domain is unstructured.¹⁸ Taking inspiration from this model, we propose that helix 9 is unstructured in the intermediate state. In our model, M182T stabilizes helix 9’s native conformation and reduces its conformational heterogeneity. Because this helix is an important part of the interface between the α-helix and β-sheet domains, we propose that stabilizing the helix stabilizes the entire interface between the two domains, thereby stabilizing TEM’s native conformation. Helix 9 being unstructured in the intermediate state in our model is consistent with the fact that the free energy difference between the unfolded and intermediate states is unaffected by M182T (Table 1).

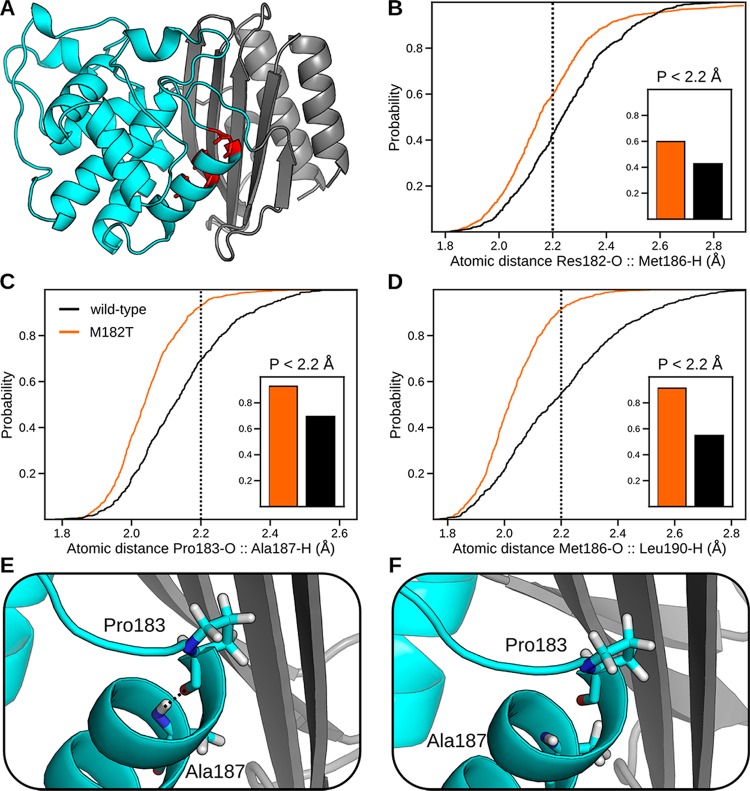
As a proxy for assessing the stability of helix 9, we quantify the distribution of distances between its backbone hydrogen-bonding partners. These distance distributions are population-weighted statistics of representative conformations from each state in the MSMs we built from our FAST simulation data sets, and they capture transitions between weak and moderate hydrogen bonds. Following past work,^19,20 we define a moderate hydrogen bond as having a hydrogen bond acceptor to hydrogen distance less than 2.2 Å, where a weak hydrogen bond has a distance between 2.2 and 2.5 Å. Assuming that weak hydrogen bonds are more likely to break on longer time scales, we can infer M182T’s effect on helix stability by comparing the local fluctuations of its hydrogen bonds to that of wild-type.

Quantifying the distance distributions of hydrogen bonds reveals that M182T stabilizes helix 9. M182T increases the probability of moderate strength hydrogen bonds between three pairs of residues: 182–186, 183–187, and 186–190 (Figure 3). As stated above, since moderate strength hydrogen bonds are less likely to break, we conclude that they are stabilizing. The distributions for other hydrogen bonds are not altered significantly by the M182T substitution. Interestingly, all the residues with increased hydrogen-bonding strength reside on the face of the helix that points into the core of the protein, along the interface between the two domains (Figure 3A).

Figure 3.

Effect of M182T on the stability of helix 9, as judged by the distributions of distances between hydrogen-bonding partners. (A) Structure highlighting hydrogen-bonding partners residue 182 and Met186, Pro183 and Ala187, and Met186 and Leu190, which are colored red. (B–D) Cumulative distribution functions, calculated from population-weighted statistics from MSMs of our FAST simulations, of the hydrogen-bonding partners listed in panel A for wild-type (black) and M182T (orange). These plots indicate the probability of observing an atomic distance less than the specified value. Our cutoff distance for moderate hydrogen bonds, 2.2 Å, is shown as a dotted line. Probabilities of moderate hydrogen bonds for each pair are shown in the inset. (E, F) Representative structures, from our MSMs, of helix 9 with a moderate hydrogen bond (observed in M182T) and a broken hydrogen bond (observed in wild-type). The backbone of the α-helix domain (cyan) and β-sheet domain (gray) are represented as a cartoon.

Helix Capping Alone Is Not Sufficient To Stabilize the Native State

Mutagenesis at position 182 presents a valuable opportunity to test our model and probe why other mutations may or may not stabilize helix 9. In particular, studying other capping residues could reveal that capping is sufficient for stabilization or, alternatively, lead to the identification of other stabilizing factors. To discover these factors, we modeled mutations at position 182, predicted their stability relative to wild-type, and performed experimental tests.

We selected three alternative substitutions at position 182 to study. First, we selected M182N because asparagine is the most frequently observed N-capping residue in proteins with known structures²¹ and the most stabilizing,²² so one might expect it to be even more stabilizing than threonine. Second, we chose M182S because serine has a hydroxyl group that is analogous to threonine’s, so it might form a similar capping interaction and have a comparable effect on stability. Third, we modeled M182V because valine mimics threonine sterically but lacks the ability to cap since it has a methyl group instead of a hydroxyl group. Therefore, comparing M182V with the other substitutions could help elucidate the relative importance of capping and sterics.

Consistent with our expectations, MSMs predict that M182S and M182N cap helix 9 (Figure S1). The probabilities that Ser182 and Asn182 cap by hydrogen bonding with Ala185 are 0.61 ± 0.02 and 0.79 ± 0.02, respectively. Each residue can also hydrogen bond with Glu64 in the s2h2 loop. M182S forms this interaction with a probability of 0.22 ± 0.02, and M182N forms this interaction with a probability of 0.59 ± 0.03. Notably, M182N has the ability to simultaneously cap helix 9 and interact with the s2h2 loop. Therefore, if capping were sufficient to predict helix stability, we would expect that M182S and M182N would be stabilizing mutations, while M182V would not.

Quantifying the degree to which each of these substitutions stabilizes helix 9 suggests that capping is not sufficient to stabilize TEM. Comparing the probabilities of moderate hydrogen bonds along the length of helix 9 reveals that M182S is predicted to be stabilizing, whereas M182V and M182N are not (Figure S2). The fact that M182N is not predicted to be stabilizing is particularly surprising given that it caps as frequently as M182T and can simultaneously hydrogen bond with Glu64. If true, this would highlight the predictive power of our model, since it defies biochemical intuition. To test these predictions, we experimentally measured the stability of each TEM variant.

Free energy differences of each variant, derived from chemical melts, and a crystal structure are consistent with our model for global stability. As predicted, M182S stabilizes TEM to a similar extent to M182T (Table 1, Figure S3). Furthermore, M182N and M182V are not stabilizing. To provide additional evidence that M182N caps helix 9 without conferring stability, we solved a crystal structure of this variant to 2.0 Å resolution (Figure S4, Table S1). This structure further supports our prediction that Asn182 caps, since the X-ray density around position 182 is best fit with a rotamer that caps helix 9 by hydrogen bonding with Ala185 (Figure S4). Additionally, the mutation M182N minimally affects nearby residues, as is evidenced by the RMSD to the wild-type crystal structure (PDB 1BTL) for backbone residues within 1.0 nm of position 182 being 0.45 Å. This suggests that stabilization (or destabilization) arises from changes to the probabilities of different states rather than the identity of the ground state.

Understanding why M182N does not stabilize TEM despite its strong propensity for capping helix 9 presents a valuable opportunity for dissecting the mechanisms of stabilization by M182T and M182S. Given that capping is generally stabilizing, we reasoned that Asn182 must form other interactions that counterbalance this effect. If this is true, we would expect the stability of helix 9 in isolation from the rest of the protein to correlate with the propensity of residue 182 to cap the helix. To test this prediction, we simulated helix 9 (residues 181–197) with each of the following residues at position 182: threonine, serine, asparagine, valine, and methionine. For each variant, we ran 20 simulations of 200 ns, for a total of 4 μs.

Probing the helical propensity of each variant suggests that capping is sufficient to stabilize helix 9 in isolation. We quantify helical propensity by measuring the probability that at least 80% of the residues adopt a conformation in the α-helical region of the Ramachandran plot. We find that each of the helix 9 variants with an N-terminal capping residue (Thr, Ser, or Asn) at position 182 have a similar helical propensity of ∼45% (Figure S5). Furthermore, variants that lack a capping residue have much lower helical propensity (12–23% for Val and Met). These trends remain the same if the cutoff for considering a structure helical is changed. Therefore, it appears that any capping interaction will stabilize helix 9 in isolation, consistent with our hypothesis that Asn182 must be forming other destabilizing interactions in the context of the full-length protein. To determine the reason that M182N does not stabilize helix 9 in the context of the full sequence, we next examine the differences in Asn182’s conformations between the full-length sequence and the isolated helix.

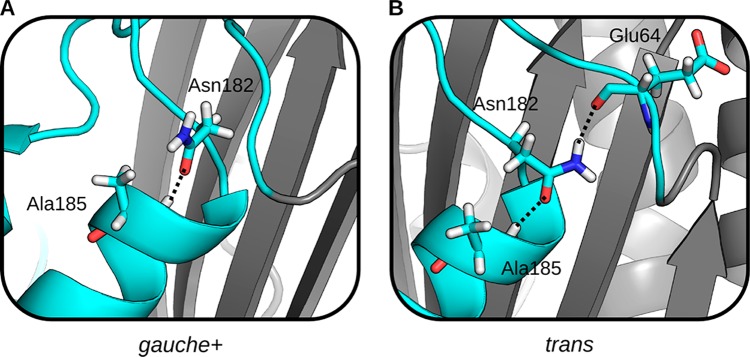
In both sets of simulation for M182N, the isolated helix and the full-length sequence, Asn182 largely populates only two conformations. These conformations differ in whether the χ₁-angle is in the gauche+ (χ₁: 0° → 120°) or trans (χ₁: 120° → 240°) rotamer. Both conformations are capable of capping helix 9, but only the trans rotamer hydrogen-bonds with Glu64 (Figures 4A and 4B). In the isolated helix, Asn182 adopts the trans rotamer with a probability of 0.75 ± 0.01, while the probability of this conformation is only 0.58 ± 0.03 in the context of the full-length protein (Figure 5). In contrast, Thr182 and Ser182 overwhelmingly adopt the gauche+ rotamer (Figure S6).

Figure 4.

Two commonly observed side chain conformations of Asn182 in MSMs, which can be characterized by their χ₁ angle. (A) A representative structure with Asn182 in the gauche+ conformation. The side chain amine points out into solution. (B) A representative structure with Asn182 in the trans conformation. The side chain amine hydrogen-bonds with Glu64 in the s2h2 loop. In both conformations, the side chain hydrogen-bonds with Ala185. The backbone of the α-helix domain (cyan) and β-sheet domain (gray) are represented as a cartoon.

Figure 5.

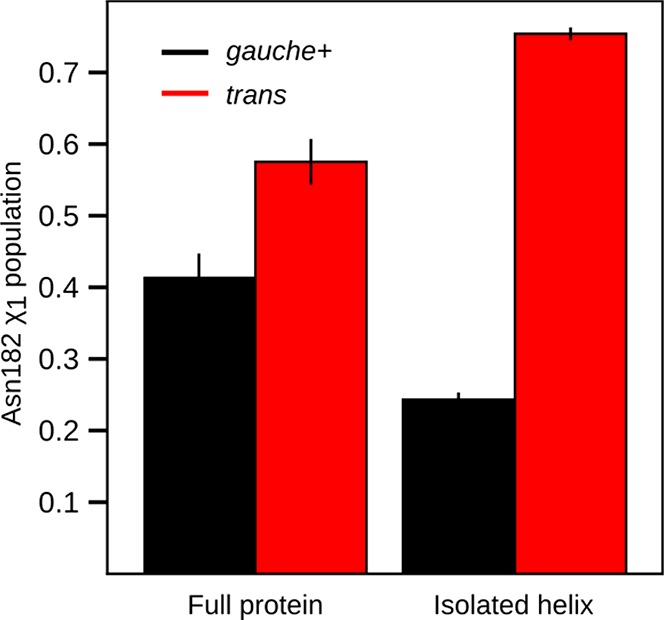
Asn182 rotamer populations for the full protein and isolated helix. Shown are the gauche+ (black) and trans (red) rotamer populations from MSMs of the full protein and isolated helix.

Asn182’s rotamer populations suggest that the trans rotamer stabilizes helix 9 but that competing interactions in the context of the full-length protein mitigate these stabilizing effects by favoring the gauche+ conformation. As a test of this hypothesis, we calculated two sets of distance distributions for hydrogen bonds along helix 9: one for the set of conformations when Asn182 is in the trans rotamer, and one for the gauche+ rotamer (Figure S7). Comparing these distributions confirms that the trans rotamer stabilizes helix 9 by increasing the probability of moderate strength hydrogen bonds, while the gauche+ rotamer behaves more like wild-type. We next examined structures from each rotameric state of Asn182 to understand why gauche+ appears so frequently given that it does not stabilize helix 9.

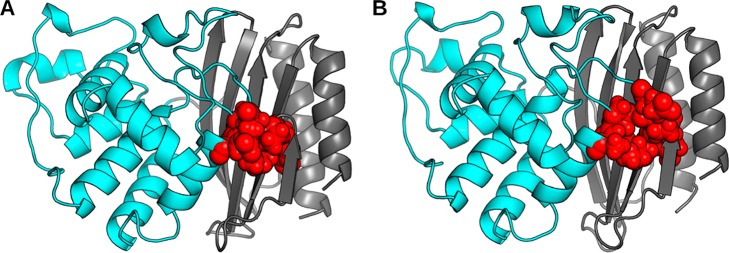
We find the trans and gauche+ conformations of Asn182 to have distinct effects on packing at the interface between the α-helix and β-sheet domains. In the gauche+ state, which does not stabilize helix 9, the domain interface is well-packed (Figure 6A). In contrast, when Asn182 adopts the trans conformation, it appears to disrupt the packing of this interface and increase the exposure of a number of hydrophobic moieties to solvent (Figure 6B). Specifically, a pocket forms between Tyr46 and Ile47 from the β-sheet domain, Pro62 and Glu63 of the s2h2 loop, and Pro183 and Ala184 of the α-helix domain. To quantify this effect, we calculated the average solvent accessible surface area of these residues for the ensembles of structures where Asn182 adopts either the trans or gauche+ rotamer. Doing so reveals that when Asn182 adopts the trans state, this surface area increases by ∼20% compared to when Asn182 is in the gauche+ state (Figure S8). Furthermore, much of the increased surface area is contributed by hydrophobic portions of these residues. Since exposure of buried hydrophobic groups is thermodynamically destabilizing, we propose that opening of this pocket counterbalances the stabilizing effects of capping. Therefore, M182N fails to stabilize helix 9 and ultimately the entire protein. This result is also consistent with the observation of the gauche+ rotamer in the crystal structure of M182N, since each rotamer has roughly equal population and crystal packing forces will favor the more compact structure. Finally, our results for Asn182 are consistent with our proposal that the domain interface is a crucial determinant of the stability of TEM’s native state.

Figure 6.

Representative structures that highlight the effects of different Asn182 rotamers on packing at the interface of the s2h2 loop and α-helix/β-sheet domains. (A) A representative structure of the gauche+ rotamer. (B) A representative structure of the trans rotamer. Residues whose packing is affected by Asn182’s rotamer (Tyr46, Ile47, Pro62, Glu63, Pro182, and Ala184) are shown as red spheres. The backbone of the α-helix domain (cyan) and β-sheet domain (gray) are represented as a cartoon.

Stabilizing Mutations Stabilize the Domain Interface

As a further test of our model, and the importance of helix 9 to the domain interface, we turned to NMR spectroscopy. We use NMR because it can provide site specific details on protein structure and dynamics. Here, we performed ¹H–¹⁵N heteronuclear single quantum coherence (HSQC) experiments for each variant and calculated chemical shift perturbations (CSPs) relative to wild-type. Since each chemical shift reports on a nucleus’s unique local magnetic environment, a CSP indicates a change in the structure and dynamics at this site. Thus, the CSPs for each variant will identify all regions affected by the mutation, regardless of their proximity to the mutation.

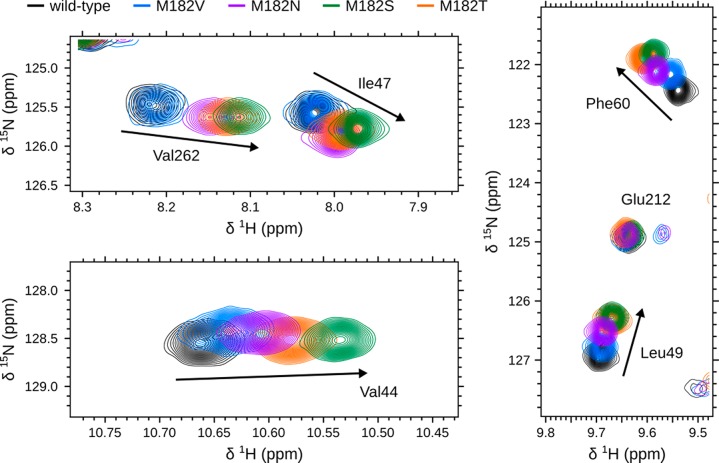
Consistent with our proposed mechanism for stabilization, most of the statistically significant CSPs for M182T are found in helix 9 and the adjacent β-sheets (Figure 7). Significant CSPs are observed on the first two turns of helix 9, as is expected from our prediction that M182T increases the propensity of moderate hydrogen bonds. We also observe significant CSPs on the β-sheet domain, not only in residues that interact directly with helix 9 (i.e., Ile47, Leu49, and Val262) but also in more distant residues (i.e., Val44, Phe60, and Thr265). Together, these results demonstrate that M182T alters the structure and dynamics of helix 9 and that these effects are propagated to distant residues along the domain interface. This is consistent with our model that M182T stabilizes helix 9, which in turn stabilizes the interface between the β-sheet and α-helix domains. To explore this idea further we next examined the CSPs of the other variants.

Figure 7.

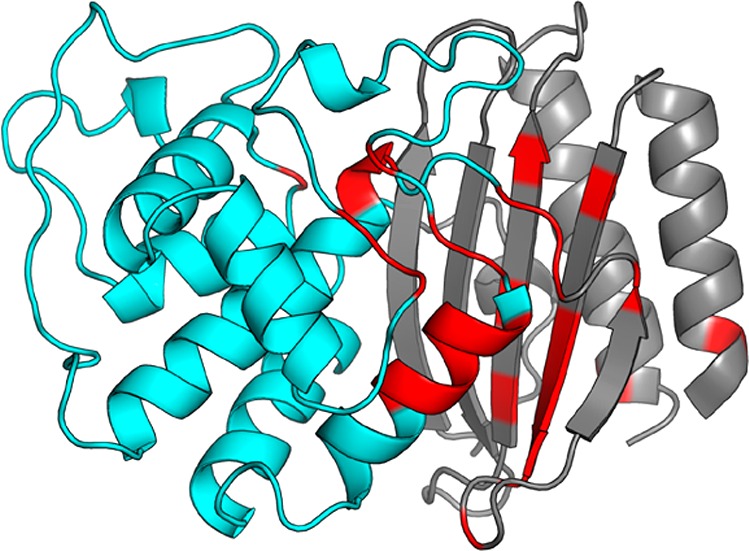
Backbone amide chemical shift perturbations of TEM M182T. The backbone of the α-helix domain (cyan) and β-sheet domain (gray) are represented as a cartoon. Residues with statistically significant chemical shift perturbations are colored red.

Comparing the magnitude and direction of CSPs on the β-sheet between each variant suggests that stabilizing mutations stabilize the domain interface. Similar to M182T, each variant predominately displays CSPs on helix 9 and the interface of the α-helix and β-sheet domains (Figure S9). This indicates that each of our substitutions at position 182 alters the structure and dynamics of the domain interface. Although one might conclude from the common locations of CSPs between the variants that each mutation perturbs TEM in a similar manner, we find that the magnitude of CSPs on the β-sheet differs between variants (Figure 8). Additionally, these CSPs are not randomly scattered. Instead, there is a clear trend from the least stable to the most stable variant. Taking all of our observations together, we propose that CSPs closer to wild-type represent a more loosely packed, weaker interface, whereas those closer to M182T/M182S represent a more tightly packed, stronger interface. Therefore, we conclude that global stability is achieved not only through helix 9 stabilization but also through stabilization of the domain interface.

Figure 8.

Representative backbone amide chemical shifts, located on TEM’s β-sheet, for 5 sequence variants. Shown are the chemical shifts for wild-type (black), M182V (blue), M182N (purple), M182S (green), and M182T (orange) for residues located on the β-sheet: Val44, Ile47, Leu49, Phe60, and Val262. For reference, Glu212 is not located on the β-sheet and does not display significant perturbations upon mutation.

Stabilizing Mutations Are Global Suppressors

If stabilization by M182T is the biophysical mechanism for its ability to suppress the impact of other deleterious mutations, then we would expect the stabilities of the three new variants we selected to correlate with their ability to act as global suppressors. To test this hypothesis, we introduced our three substitutions into a background that also contains the substitution G238S. G238S is known to confer TEM with cefotaxime resistance at the expense of protein stability.^1,2,5 Furthermore, a variant with both G238S and M182T is more resistant to cefotaxime than a variant with just one of these substitutions. Therefore, we expect M182S/G238S to have similar levels of cefotaxime resistance to M182T/G238S while we expect M182N/G238S and M182V/G238S to have similar levels of cefotaxime resistance to G238S alone.

Minimal inhibitory concentrations (MICs) of bacteria expressing our TEM variants in the background of G238S in the presence of varying levels of cefotaxime reveal that global stabilization of the domain interface leads to global suppression. As predicted, M182S/G238S resembles M182T/G238S while the other variants are more similar to G238S alone (Table 2). The observation that M182S is a global suppressor mutation that has not been reported previously led us to question if other global suppressors may exist.

Table 2. MICs for Escherichia coli Strains Expressing TEM β-Lactamase Variants^a.

	cefotaxime (μM)
	single mutant	double mutant (+G238S)
wild-type TEM	<0.035	0.141
Suppressor/Stabilizing
M182T	0.070	72.000
M182S	0.070	36.000
Wild-Type-like/Neutral
M182V	<0.035	0.141
M182N	<0.035	0.141
M182C	<0.035	0.281
M182A	<0.035	0.281
Deleterious
M182G	ndb	<0.035
M182P	nd	<0.035
M182I	nd	<0.035
M182L	nd	<0.035
M182F	nd	<0.035
M182W	nd	<0.035
M182Y	nd	<0.035
M182R	nd	<0.035
M182H	nd	<0.035
M182 K	nd	0.070
M182D	nd	<0.035
M182E	nd	<0.035
M182Q	nd	<0.035
M182G	nd	<0.035

^aMIC determination was performed in triplicate. Values are most commonly observed concentration with an error of ± one well, which differ by 2-fold in concentration.

^bNot determined.

MICs for every other possible variant at position 182, in combination with G238S, reveal that there are no other possible global suppressor mutations at this position (Table 2). Substituting Met182 with valine, asparagine, cysteine, or alanine in a G238S background is neutral. All other double mutants have lower MICs than G238S alone, suggesting that they are deleterious. Therefore, M182T and M182S are the only global suppressor mutations at this residue. Together with the previous sections, these results are consistent with our hypothesis that stabilization of helix 9 and the domain interface are responsible for M182T’s ability to stabilize TEM and suppress the effects of other destabilizing substitutions.

Conclusions

Our MSMs have provided a new mechanistic understanding of the stabilizing effects of M182T, which we successfully use to predict the effects of new mutations at position 182. Previous crystallographic studies have proposed that M182T’s stabilizing effect is a result of Thr182 either N-capping or forming a hydrogen bond between the α-helix and β-sheet domain interface. Since MSMs are able to capture conformational heterogeneity in a way that cannot be inferred from static structures, we are able to propose that M182T stabilizes helix 9, which in turn stabilizes the interface between the α-helix and β-sheet domains. In support of the validity of our model, it has superior predictive power compared to previous models: we correctly predict that M182S is stabilizing but not M182V and M182N, whereas the hydrogen-bonding model incorrectly predicts M182N to be stabilizing. Furthermore, NMR chemical shift perturbations support our dynamical predictions. The fact that our MSMs make successful predictions that defy biochemical intuition is a strong testament to the accuracy and value of these atomically detailed models.

The ability to predict new stabilizing mutations is an important step toward designing proteins with new or improved functions. The fact that M182S has not been observed suggests that nature has not exhaustively identified all possible stabilizing mutations. Our work raises interesting questions, such as why M182S has not been observed in nature. Furthermore, combining our ability to predict new stabilizing mutations with our previous work on predicting how mutations impact activity could enable the design of proteins with new or improved function.

Methods

MD Simulations

All simulations were run with Gromacs 5.1.1.²³ β-Lactamase simulations were run at 300 K using the AMBER03 force field with explicit TIP3P solvent.^24,25 We have previously shown that the AMBER03 force field is sufficient to capture the relevant conformational states of TEM β-lactamases for a range of problems, including the identification of cryptic pockets, the design of allosteric drugs, and predicting the effects of mutations.^11,26−28 The single starting structure for TEM-1 β-lactamase simulations was generated from the crystallographic structure (PDB ID: 1JWP).¹ The starting structures for each TEM variant was generated by mutating the side chain at position 182 to the respective amino acid using PDBFixer, followed by an energy minimization for 1,000 steps using the AMBER03 force field with the OBC GBSA implicit solvent model.^24,29,30 Starting structures for the individual helix simulations were taken as residues 181–197 from the starting structures of the full sequence. For each full-length sequence, 2.5 μs of conventional sampling and 4 μs of FAST-RMSD adaptive sampling (described below) were performed. For the individual helix simulations, 4 μs of each sequence was performed: 20 simulations of 200 ns.

Simulations were prepared by placing the starting structure for each sequence in a dodecahedron box that extended 1.0 Å beyond the protein in any dimension. Each system was then energy minimized with the steepest descent algorithm until the maximum force fell below 100 kJ/mol/nm using a step size of 0.01 nm and a cutoff distance of 1.2 nm for the neighbor list, Coulomb interactions, and van der Waals interactions. For production runs, all bonds were constrained with the LINCS algorithm and virtual sites were used to allow a 4 fs time step.^31,32 Cutoffs of 1.0 nm were used for the neighbor list, Coulomb interactions, and van der Waals interactions. The Verlet cutoff scheme was used for the neighbor list. The stochastic velocity rescaling (v-rescale) thermostat was used to hold the temperature at 300 K.³³ Conformations were stored every 20 ps.

Adaptive Sampling

The FAST algorithm was used to generate simulation data.¹⁵ FAST-RMSD was run for each sequence for 10 rounds, of 10 simulations per round, where each simulation was 40 ns in length: a total of 4 μs per sequence. The FAST-ranking favored states that maximized the RMSD to the starting structure. RMSD calculations were performed between all heavy atoms in residues within 1.0 nm of position 182 in the crystallographic starting structure. To enhance the conformational diversity of states that are chosen for reseeding simulations, the FAST-ranking function was modified with a term that penalizes states conformationally similar to others selected. This ensures that each round of sampling contains a good spread of conformations. Procedurally, states are selected one at a time, where the modified term is recomputed and added to the original ranking for each selection. The modified ranking takes the form

where ϕ̅ is the directed component, ψ̅ is the undirected component, and α and β control the weights of ψ̅ and χ respectively. Here, ψ̅(i) is taken to be the state counts and a value of 1 was used for both α and β. The additional term,

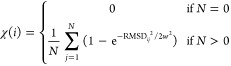is calculated as the average of Gaussian weighted RMSDs from state i to the N states that have been selected for reseeding so far, where w is the Gaussian width (set to the clustering radius). Thus, the procedure for selecting states to reseed simulations from each round is as follows: (1) rank all states by the FAST-ranking and select the top state as the first state to reseed, (2) add the similarity penalization term to the FAST-ranking and select the top state as another state to reseed, and (3) update the penalization term and repeat step 2 until the desired number of states for reseeding have been selected.

MSM Construction and Analysis

All MSMs were built using MSMBuilder.^34,35 An MSM is a network representation of an energy landscape, where nodes are discrete conformational states and directed edges are conditional transition probabilities. MSMs provide a statistically rigorous way of mapping of protein dynamics, even from parallel simulations with starting structures that are not Boltzmann distributed. Using an MSM, we can quantify thermodynamic and kinetic changes that aid in understanding molecular motions.

Simulation data sets for each TEM variant were combined and clustered into a single shared state-space. Each data set consisted of 4 μs FAST-RMSD and 2.5 μs conventional simulations. With 5 sequences, this gives a total of 32.5 μs of total simulation. The shared state-space was defined using all heavy atoms on residues within 1.0 Å of position 182 in the crystallographic structure of TEM β-lactamase (PDB ID: 1JWP). The side chain atoms of position 182 were not included, since they vary between sequences. These atomic coordinates were then clustered with a k-centers algorithm based on RMSD between conformations until every cluster center had a radius less than 1.0 Å. Then, 10 sweeps of a k-medoids update step was used to center the clusters on the densest regions of conformational space. Following clustering, the cluster assignments were split and a unique MSM was constructed for each TEM sequence with a lagtime of 2 ns. To obey microscopic reversibility, transition count matrices were symmetrized. Representative cluster centers were saved for each state in each sequence for analysis.

Geometric analysis of representative cluster centers was performed using MDTraj:³⁶ in particular, RMSDs, solvent-accessible surface areas, and atomic distances. Ensemble average values within MSMs were calculated as the expectation value for a particular observable. I.e., the expectation of observable Z is calculated as

where p(z_i) is the population of state i and z_i is the value of state i. All cumulative distribution functions were generated with population-weighted statistics of representative conformations from each state in the MSMs we built from our FAST simulation data sets. Each point in one of these cumulative distribution functions is calculated as

where p(z_i) is the population of state i.

Protein Expression and Purification

TEM-1 was subcloned using NdeI and XhoI restriction sites into the multiple cloning site of a pET24 vector (Life Technologies), and its native export signal sequence was replaced by the OmpA signal sequence to maximize export efficiency. Site-specific variants were constructed via site-directed mutagenesis and verified by DNA sequencing. Plasmids were then transformed into BL21(DE3) Gold cells (Agilent Technologies) for expression under T7 promoter control.

Cells were induced with 1 mM IPTG at OD = 0.6 and grown at 18 °C for 15 h before harvesting. TEM β-lactamases were isolated from the periplasmic fraction using osmotic shock lysis: Cells were resuspended in 30 mM Tris pH 8, 20% sucrose and stirred for 10 min at room temperature. After centrifugation, the pellet was resuspended in ice-cold 5 mM MgSO₄ and stirred for 10 min at 4 °C. After centrifugation, the supernatant was dialyzed against 20 mM sodium acetate, pH 5.5, and purified using cation exchange chromatography (BioRad UNOsphere Rapid S column) followed by size exclusion chromatography (BioRad ENrich SEC 70 column) into storage buffer (20 mM Tris, pH 8.0).

Protein Stability Measurements

Fluorescence data were collected using a Photon Technology International QuantaMaster 800 rapid excitation spectrofluorometer with Quantum Northwest Inc. TC-125 Peltier-controlled cuvette holder. Melts were performed by monitoring intrinsic protein fluorescence, exciting at 280 nm and detecting emission intensity at 340 nm. Melts were carried out in a 1 cm path length cuvette (50 μg/mL protein, 20 mM Tris pH 7). Samples with varying concentrations of urea were prepared individually, equilibrated overnight, and stirred in the instrument for 2 min before data collection.

Circular dichroism data were collected using an Applied Photophysics Chirascan with a Quantum Northwest Inc. TC-125 Peltier-controlled cuvette holder. Melts were performed by monitoring the CD signal at 222 nm and were carried out in a 1 cm path length cuvette (50 μg/mL protein, 20 mM Tris pH 7). For urea melts, samples with varying concentrations of urea were prepared individually, equilibrated overnight, and stirred in the instrument for 2 min before data collection, which was averaged over 60 s.

Urea melt data for each variant were globally fit. Fluorescence data were fit by a two-state model (I-to-N), and CD data simultaneously were fit by a three-state model (U-to-I-to-N) using a linear extrapolation method:³⁷

1

2

where F_i and F_n are the fluorescence signals for the intermediate and native states, fit as lines, and Θ_u, Θ_i, and Θ_n are the CD signals for the unfolded, intermediate, and native states, fit as lines. ΔG_in is the extrapolated free energy of folding relative to the intermediate in the absence of denaturant, and m_in is a proportionality constant related to the steepness of the I-to-N transition. ΔG_ui and m_ui are the free energy and m-value describing the U-to-I transition.

The m_ui-value was fixed to 1.7 kcal/mol·M, the average derived for wild-type TEM, because we hypothesize that the intermediate species is the same between variants. m-values correlate with the change in solvent-exposed surface area upon folding¹² and are characteristic of a particular folded or partially folded state. For comparison, all data were also fit using a floating m_ui-value, and F-tests were performed with the null hypothesis that any improvement to the fit due to the additional parameter occurs by chance. The F-values obtained were all in the range of 1 × 10^–10 to 1 × 10^–7 (much lower than ∼4.2, the critical F-value for p < 0.05), and thus the F-tests strongly support our hypothesis that holding the m_ui-value fixed is reasonable.

Minimal Inhibitory Concentration (MIC) Measurements

Levels of antibiotic resistance of BL21(DE3) cells containing TEM expression plasmids were determined by measuring their minimum inhibitory concentrations (MIC90s) using the broth microdilution method according to the Clinical and Laboratory Standards Institute (CLSI, formerly the NCCLS) guidelines.³⁸ Strains were grown to saturation overnight in Luria Miller broth with kanamycin and 1 mM IPTG. Each well of a 96-well microtiter plate was filled with 50 μL of sterile Mueller Hinton II (MHII) medium broth (Sigma). Antibiotic was dissolved in water making a 20 mM solution and then diluted with sterile MHII medium broth to 288 μM cefotaxime (CFX). Exactly 50 μL of the compound solution was added to the first well of the microtiter plate, and 2-fold serial dilutions were made down each row of the plate. Exactly 50 μL of bacterial inoculum (diluted to 5 × 10⁵ CFU mL^–1 from the overnight cultures) was then added to each well, giving a total volume of 100 μL well^–1 and compound concentration gradients of 72–0.04 μM CFX. The plate was incubated at 37 °C for 17 h, and then each well was examined for bacterial growth. The MIC90 was recorded as the lowest compound concentration required to inhibit 90% of bacterial growth as judged by turbidity of the culture medium relative to a row of wells filled with a water standard. Gentamicin was included in a control row at a concentration gradient of 174–0.09 μM.

Nuclear Magnetic Spectroscopy

Uniform ¹⁵N labeled TEM-1 was expressed in M9 minimal medium containing ¹⁵NH₄Cl (1 g/L), d-glucose (4 g/L), and 2.5 mM betaine. The cells were incubated at 37 °C and 240 rpm until OD₆₀₀ ≫ 0.6, and then for an additional 30 min at 18 °C and 225 rpm. Cells were induced with IPTG and incubated approximately 36 h prior to harvesting. Protein was purified from both the periplasm and the medium; the medium was concentrated to approximately 100 mL using an Amicon stirred cell (EMD Millipore) and dialyzed overnight into TEM-1 S loading buffer. Purification followed the periplasmic prep.

¹⁵N/¹H HSQC spectra were recorded at 303 K on a 600 MHz (1H) Bruker Avance III spectrometer. TEM-1 samples were concentrated to 100 μM in 25 mM sodium phosphate, 4 mM imidazole pH 6.6, and 10% D₂O. Wild type TEM-1 assignments were previously reported (BMRB entry 16392).³⁹

X-ray Crystallography

Screening for crystal growth conditions was performed with Mosquito (TTP LabTech Limited) using 25 mg/mL protein. Optimized crystals were grown via hanging drop vapor diffusion at 18 °C by mixing 1 μL of protein at 25 mg/mL with 1 μL of reservoir containing 0.1 M sodium phosphate dibasic/citric acid pH 4.2, 0.1 M lithium sulfate, and 20% PEG 1000. Crystals were cryoprotected in oil (Hampton Research Parabar 10312 HR2-862) before flash-freezing in liquid nitrogen. X-ray diffraction data was collected at beamline 4.2.2 of the Advanced Light Source in Berkeley, CA, and processed with XDS.⁴⁰ Phase determination was by molecular replacement using PHENIX⁴¹ with the coordinates from PDB 1JWP used as a search model. Iterative model building in COOT⁴² and refinement with PHENIX⁴¹ accounting for crystal twinning led to the current model of M182N with R_work/R_free of 22.46%/28.26%. The final refined model had a Ramachandran plot with 96.54% of residues in the favored region and none in the disallowed region (MolProbity).⁴³ A summary of the data collection and refinement statistics is shown in Table S1. Structure factors and coordinates are deposited in the RSCB Protein Structure Database under PDB ID 6B2N.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.7b00465.

• Distance distributions, helical propensities, rotamer probabilities, and solvent accessibility of TEM variants from MSMs, chemical melts, crystallographic structure and parameters, and NMR chemical shift perturbations (PDF)

Author Present Address

^§ K.M.H.: Department of Chemistry, Williams College, 880 Main Street, Williamstown, MA 01267.

Author Contributions

^‡ M.I.Z. and K.M.H. contributed equally to this work.

The authors declare no competing financial interest.