The regulation of pH across the t-system membrane of skeletal muscle fibers is poorly understood. Using a sealed tubule preparation, Launikonis et al. reveal Na+/H+ exchange activity and characterize the properties of the diffusional and NHE proton fluxes across the t-system.
Abstract
The complex membrane structure of the tubular system (t-system) in skeletal muscle fibers is open to the extracellular environment, which prevents measurements of H+ movement across its interface with the cytoplasm by conventional methods. Consequently, little is known about the t-system’s role in the regulation of cytoplasmic pH, which is different from extracellular pH. Here we describe a novel approach to measure H+-flux measurements across the t-system of fast-twitch fibers under different conditions. The approach involves loading the t-system of intact rat fast-twitch fibers with a strong pH buffer (20 mM HEPES) and pH-sensitive fluorescent probe (10 mM HPTS) before the t-system is sealed off. The pH changes in the t-system are then tracked by confocal microscopy after rapid changes in cytoplasmic ionic conditions. T-system sealing is achieved by removing the sarcolemma by microdissection (mechanical skinning), which causes the tubules to pinch off and seal tight. After this procedure, the t-system repolarizes to physiological levels and can be electrically stimulated when placed in K+-based solutions of cytosolic-like ionic composition. Using this approach, we show that the t-system of fast-twitch skeletal fibers displays amiloride-sensitive Na+/H+ exchange (NHE), which decreases markedly at alkaline cytosolic pH and has properties similar to that in mammalian cardiac myocytes. We observed mean values for NHE density and proton permeability coefficient of 339 pmol/m2 of t-system membrane and 158 µm/s, respectively. We conclude that the cytosolic pH in intact resting muscle can be quantitatively explained with respect to extracellular pH by assuming that these values apply to the t-system membrane and the sarcolemma.
Introduction
Ion transport mechanisms in the plasma membrane (Na+/H+ exchange [NHE], Na+/bicarbonate cotransport, and lactate/H+ cotransport) play the key role in regulating the intracellular proton concentration in mammalian skeletal muscle (Juel, 2008) within the range that is critically important for cellular function (30–200 nM; pH 6.7–7.5). If protons were passively distributed across the membrane (∼740 nM at electrochemical equilibrium for a membrane potential of −75 mV and 7.40 extracellular pH), the proton concentration would be cytotoxic: it would impair not only muscle performance (Knuth et al., 2006), but also DNA and RNA synthesis, protein synthesis, glycolysis, and respiratory activity (Madshus, 1988).
The largest membrane interface between myoplasm and extracellular fluid in skeletal muscles—up to 80% of total plasma membrane surface—is represented by the tubular system (t-system), but its capacity to regulate intracellular pH is not well understood. A recent study by Garciarena et al. (2013) showed the absence of functional NHE exchangers in the t-system of mammalian ventricular myocytes. Unlike ventricular muscle, skeletal muscle can function under hypoxic conditions when large amounts of protons/lactic acid are produced that need to be promptly extruded to prevent damage. Although it is long established that the NHE system is a major mechanism for proton extrusion in skeletal muscle (Aickin and Thomas, 1977; Hoffmann and Simonsen, 1989; Juel, 2000), little is known about proton fluxes across the t-system membranes of skeletal muscle and how these fluxes are regulated by changes in the cytosolic ionic composition.
The aim of this study was to test whether an NHE system is functional in the t-system of fast-twitch mammalian skeletal muscle fibers and, if so, determine its role in handling proton fluxes across the tubular membrane in the absence of confounding proton fluxes associated with the Na+/bicarbonate cotransport and lactate/H+ cotransport systems. For this, we used a novel approach in which we loaded dominant exogenous pH buffers (20 mM HEPES and 10 mM hydroxypyrene-1,3,6-trisulfonic acid [HPTS]) within the t-system of intact fast-twitch muscle fibers before the t-system was sealed off by removing the surface membrane by microdissection, a procedure known as mechanical skinning (Launikonis and Stephenson, 2001, 2002a,b, 2004; Launikonis et al., 2003; Ørtenblad and Stephenson, 2003). Then, given the relative spatial homogeneity of the t-tubules, we used confocal microscopy to track in xy-mode with high temporal resolution the fluorescence of the pH-sensitive dye (HPTS) trapped within the sealed t-tubules, when the pH and the ionic composition on the cytosolic side of the t-tubules was suddenly altered. The large surface-to-volume ratio of the t-tubules containing the added pH buffers enabled us to derive the H+-fluxes across the t-system membrane from the measured pH changes and demonstrate the presence of a functional NHE system in the t-system of skeletal muscle and characterize its properties, as well as those associated with diffusional proton fluxes across the t-system membranes.
Materials and methods
All experimental methods were approved by the Animal Ethics Committee at the University of Queensland. Male Wistar rats aged 2–3 mo (250–300 g) were killed by CO2 asphyxiation, and the extensor digitorum longus (EDL) muscles were rapidly excised. Muscles were then thoroughly blotted on filter paper and placed in a Petri dish under paraffin oil above a layer of Sylgard.
Intact fiber bundles were isolated under oil and exposed for at least 10 min to a Na+-based physiological solution (external solution) containing (mM) 10 HPTS, 2.5 CaCl2, 132 NaCl, 1 MgCl2, 3.3 KCl, and 20 HEPES, and pH was adjusted to 7.4 with NaOH. 5 mM sulforhodamine B (SRB), a fluorescent dye that is not sensitive to pH, was used in some batches of external solutions to normalize the HTPS signal throughout an experiment.
After exposure to the HPTS-containing external solution, single fibers were isolated under paraffin oil from the fiber bundle and mechanically skinned, a procedure that removes the surface membrane of the fiber and at the same time seals the t-system with the pH-sensitive dye in it (Stephenson and Lamb, 1993; Launikonis and Stephenson, 2001, 2002a,b, 2004; Launikonis et al., 2003). After skinning, the fiber was transferred to an experimental chamber containing a K+-based internal solution that allowed the sealed t-system to generate a normal resting membrane potential (Lamb and Stephenson, 1990, 1994). The solution contained (mM) 1 Mg2+, 49 hexamethylene 1,6-diamino tetraacetate, 1 EGTA, 10 HEPES, 103–106 K+, 36 Na+, 8 ATP, 10 creatine phosphate, 103–107 sucrose, and 0.05 N-benzyl-p-toluenesulfonamide (BTS), with pH adjusted (with KOH) to 6.6–7.7. Note that BTS specifically inhibits the contraction of fast-twitch (type II) skeletal muscle fibers. The fiber was then clamped onto the coverslip that formed the base of the experimental chamber, and the chamber was placed on the stage of an Olympus confocal laser-scanning inverted microscope. The preparation was viewed through a 40× water immersion lens. In other solutions, all K+ was replaced with Na+ to fully depolarize the t-system (Lamb and Stephenson, 1990, 1994) and raise the sodium concentration to the same level as that in the sealed t-system.
The laser 488-nm excitation line was used for HPTS, and the HPTS-emission fluorescence signal was collected in the range 490–540 nm. The laser 543-nm excitation line was used for SRB, and the SRB-emission signal was collected over the range 550–666 nm. When both HPTS and SRB signals were recorded, the signals were simultaneously imaged in xyt mode by line-interleaving the 488- and 543-nm excitation laser lines.
Imaging was in xyt mode, where single images were captured every 1.1 s. The aspect ratio of the images was 640 × 320, with the long aspect of the image parallel to the length of the fiber. This approach reduced bleaching of the t-system trapped dye per volume of excited t-system by scanning a large volume of the fiber and averaging the collected signal across the imaged section of preparation. We also used GaAsP detectors instead of the conventional PMTs so that we could collect light at lower laser excitation intensities. Furthermore, we monitored the fluorescence response in standard Na-based solutions throughout an experiment to ensure correct pH calibration of the fluorescence signals. The experiments were performed at room temperature (23 ± 1°C).
Calibration of the pH-dependent HTPS fluorescence signal in external solution
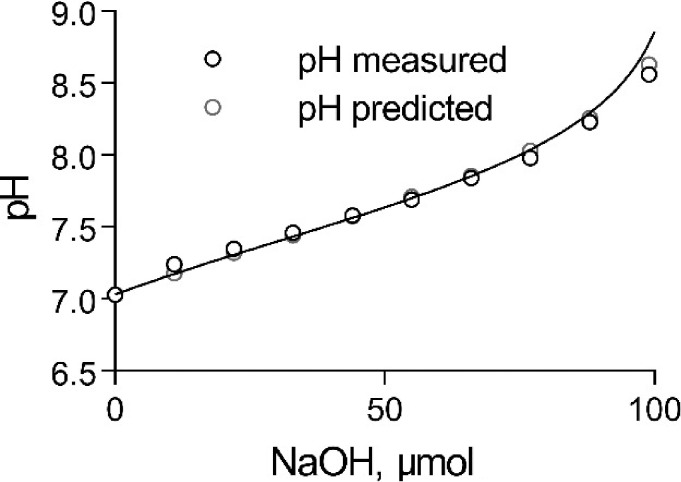
Fig. 1 shows the pH dependence of HTPS-emitted fluorescence intensity at single wave excitation (488 nm) in the external physiological solution. Because HPTS quenches at acidic pH (Willoughby et al., 1998), the data points were fitted by the following equation:
| (1) |
where Fi is the HPTS fluorescence signal at a particular proton concentration ([H+]i), Fmax is the maximum HPTS-emitted fluorescence intensity at very alkaline pH, and KHPTS is the dissociation constant (proton concentration where 50% of Fmax is obtained). Eq. 1 can be rewritten as
where pKHPTS = –log KHPTS and pHi = −log [H+]i. From Fig. 1, the best fit was obtained for pKHPTS = 7.38 ± 0.02.
Figure 1.
The pH dependence of HTPS fluorescence as determined on the confocal microscope. The pH dependence of HPTS fluorescence was measured in external physiological solution containing (mM) 10 HPTS, 2.5 CaCl2, 132 NaCl, 1 MgCl2, 3.3 KCl, and 20 HEPES, pH adjusted with NaOH.
Knowing the value of pKHPTS, according to Eq. 1′, the pH of the external solution is related to F as follows:
| (2) |
If F1 is the HPTS-emitted fluorescence intensity in the external solution at a known pH, pH1, then from Eq. 1′ it follows that
| (3) |
The expression of Fmax given by Eq. 3 can now be substituted into Eq. 2, leading to the following equation:
| (4) |
Therefore, any pH in the external physiological solution can be accurately assessed from the corresponding HPTS-emitted fluorescence intensity F as long as pKHPTS and the HPTS fluorescence intensity, F1, of the external physiological solution for a given pH (pH1) are known.
Calibration of HPTS fluorescence signals from within the sealed t-system
Monensin is a rapidly acting, selective proton and sodium ionophore that acts principally as a proton sodium exchanger (Mollenhauer et al., 1990). It is ideally suited to calibrate the HPTS fluorescence signal from the sealed t-system in Na-based cytosolic solutions, where the Na concentration is similar to that in the t-system. Thus, after treatment with monensin, the pH in the sealed t-system is expected to equilibrate to the same value as that in the Na-based cytosolic solution.
The fluorescence intensity measurements made from the sealed t-system included the background fluorescence level, B, for a particular fiber because the background fluorescence intensity cannot be accurately measured around the tubules due to the limited spatial resolution between the tubular networks. Measurements of the fluorescence intensities in three Na-based solutions (F1M, F2M, and F3M) of different pH (pH1, pH2, and pH3) after treatment with monensin permits determination of pKHPTS, maximum HPTS-emitted fluorescence intensity, Fmax, and background fluorescence, B, for a particular fiber using the following set of equations:
where
| (5) |
The pKHPTS value in the sealed t-system from measurements of 16 preparations after treatment with 20 µM monensin was 7.31 ± 0.06, which is not statistically distinct from 7.38 ± 0.02 measured in the HPTS-containing external solution in which the muscle fibers were equilibrated before the t-system was sealed.
Note that monensin is difficult to wash out, and therefore it can contaminate the endogenous NHE system if freshly dissected fibers are transferred to chambers in which monensin was previously present. To avoid contamination, chambers were discarded after exposure to monensin.
Proton buffering capacity of the sealed t-system
Before being sealed, the t-system was equilibrated in the external solution that contained two membrane-impermeant pH buffers: HEPES (20 mM), which has a pKHEPES value of 7.50 at 23°C (Good et al., 1966) and HPTS (10 mM), which under our conditions has a pKHPTS value of 7.38 as determined from Fig. 1. (Note that HPTS carries between four and five negative charges in the pH range investigated [6.6–8.5]; to avoid marked osmotic effects, HEPES was used as additional pH buffer to enhance the pH buffering capacity of the external solution.) The total concentration of protons bound by the two pH buffers at any given pH >6, Htotal, is given by the following expression:
| (6) |
The proton buffering capacity of the external solution (without SRB) was determined experimentally by titrating the solution with NaOH as shown in Fig. 2. At pH 7.03, where the titration was started, Htotal = 21.85 mM. Addition of NaOH was neutralized by protons released from the two buffers, inducing a change in pH. The solid line in Fig. 2 shows the predicted change in pH of the external solution based on Eq. 6 when NaOH was added. The very good fit between the observed and the predicted values gives confidence that Eq. 6 accurately depicts the pH buffering properties of the external solution and that the value of pKHPTS under our conditions is close to 7.38.
Figure 2.
The pH-buffering capacity of the HTPS-containing external (t-system) solution. Titration of 5 ml HPTS solution with NaOH and predicted pH curve from Eq. 6.
Proton fluxes across the t-system membranes (ΦH−t) can be calculated from the rate of the pH-dependent changes in the total amount of dissociable protons in the t-system, Ht:
| (7) |
where SAt is the surface area of the t-system. When ΦH−t > 0, protons move into the lumen of the t-system, and when ΦH−t < 0, protons move out of the t-system into the cytosolic solution. For pH values in the t-system greater than 6.5, such changes are effectively limited to changes in the amount of dissociable protons carried by the impermeant pH buffers HEPES (20 mM) and HPTS (10 mM) introduced into the t-system before it seals off when the fiber is skinned. Note that the endogenous fixed sialic acid residues in the lumen of the t-system have pK values <3, and therefore are fully dissociated at pH values >6.5. The amount of protons carried by HEPES and HPTS in the t-system is given by the following expression:
| (8) |
where Vt is the volume of the t-system and is the proton concentration in the t-system. The pK for HEPES is 7.5; the pK value used for HPTS was 7.34 (midrange between the value measured in external solution [7.38] and the value measured with monensin [7.31]). It follows that for pH >6.5, the rate of the pH-dependent changes in the total amount of dissociable protons in the t-system, Ht-sys, is
| (9) |
According to Eqs. 6 and 9, proton fluxes across the t-system membranes can be derived from the time course of proton concentration changes in the t-system lumen using the following expression:
| (10) |
where Vt/SAt is the volume-to-surface area of the t-tubules in the fiber regions where HPTS-fluorescence signals were recorded. Measurements were made only from fiber regions where transverse tubules could be clearly seen and for which the mean volume/surface area ratio (Vt/SAt) as measured by Dulhunty (1984) in rat EDL fibers was 4.1 nm. Substituting this value in Eq. 10, the proton flux across the t-system membrane measured in mol/m2/s can be calculated using the following expression, where d[H+]/dt is expressed in mol/L/s:
| (11) |
The NHE-system proton fluxes
We used the eight-state ping-pong-type NHE model with 1 H+:1 Na+ stoichiometry developed by Cha et al. (2009) to fit a variety of NHE experimental data for cardiac myocytes. The model considers that the proton NHE flux (ΦH-NHE) consists of an ion-exchange component (JH-exch) and a proton-modifier component (Mod), where the NHE exchanger has an additional intracellular proton binding site that needs to be occupied for the exchanger’s activation:
| (12) |
where CNHE is the concentration of the exchanger molecules in the t-system membrane in mol/m2, and the product JH-exch∙Mod represents the turnover rate in s−1 of the NHE molecules.
The ion exchange component (JH-exch) depends on two factors: first, the four ratios Pcyto = [H+]cyto/KH cyto, where KH cyto is the H+ dissociation constant of the NHE exchanger on the cytosolic side (=0.605 µM); Pt = [H+]t/KH t, where KH t is the H+ dissociation constant of the NHE exchanger on the t-system luminal side (=1.62 µM); Scyto = [Na+]cyto/KNa cyto, where KNa cyto is the Na+ dissociation constant of the NHE exchanger on the cytosolic side (=16.2 mM); and St = [Na+]t/KNa-t, where KNa-t is the Na+ dissociation constant on the t-system luminal side (=195 mM); and second, the four rate constants k1 (=10,500 s−1) in exchanging Na+ into the cytosol; k-1 (=201 s−1) in exchanging Na+ into the t-system; k2 (=15,800 s−1) in exchanging H+ into the t-system; and k-2 (=183,000 s−1) in exchanging H+ into the cytosol:
| (13) |
The proton-modifier component (Mod) depends on the ratios Mcyto = [H+]cyto/KM-cyto, where KM-cyto is the H+ dissociation constant of the intracellular modifier site and Mt = [H+]t/KM-t, where KM-t (=0.48 nM) is the H+ dissociation constant of the extracellular modulatory site of the proton-modifier component:
| (14) |
The relative H-NHE fluxes derived from results obtained in K-based cytosolic solutions of different pH were remarkably well fitted by the above NHE model, using the set of constants used by Cha et al. (2009) except for the value of KM-cyto in the proton-modifier component, which in our study was 14.8 nM instead of 30.7 nM to provide the best fit to our results (see T-system pH in K-based cytosolic solutions and Fig. 9 C in Results).
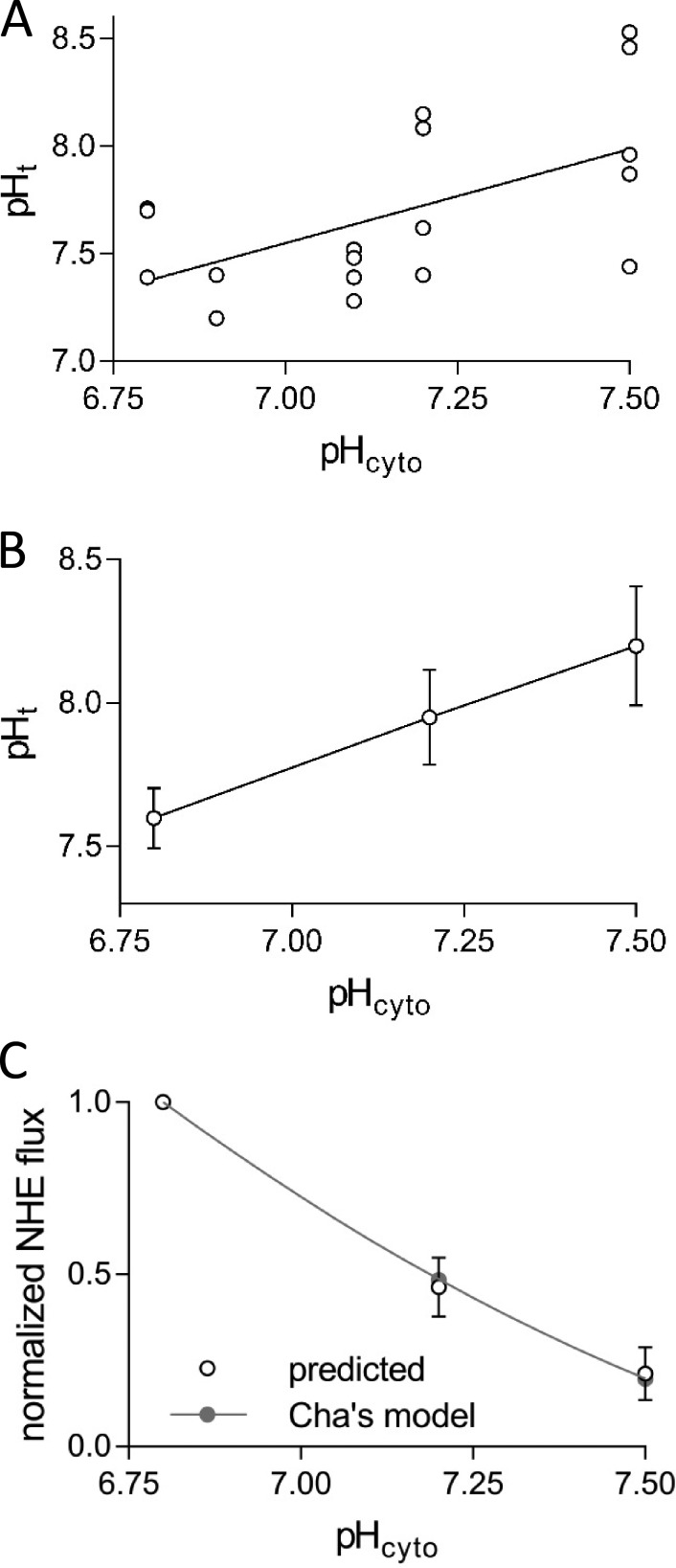
Figure 9.
The relationships between pHt and pHcyto and between NHE flux and pHcyto in polarizing, K-based solutions. (A) The steady-state pHt versus pHcyto in high [K+]cyto–based solutions in all 10 fibers investigated. (B) Result from three fibers with multiple measurements at different pHcyto plotted as means ± SEM. (C) NHE-proton flux normalized to the response in pH-6.8 K-based solution derived from the results shown in B using Eq. 20 (predicted) and expected curve for NHE proton flux based on Eq. 15, normalized to the value in pH-6.8 K-based solution (Cha’s model). Results are means ± SEM. Note that the (predicted) normalized ΦH-NHE fluxes for individual fibers changes little if the Vm value is between −75 and −90 mV.
Note that the absolute turnover rate values of the exchanger molecules are smaller by a factor f (>2) at 23°C (where our experiments were conducted) than those calculated using the rate constants derived by Cha et al. (2009) predominantly from observations made at 37°C in the Vaughan-Jones laboratory (Vaughan-Jones and Wu, 1990). This is equivalent with calculating the turnover rate at 37°C (JH-exch·Mod) using the parameter values indicated above and then reducing it by the factor f:
| (15) |
The factor f can also include a component related to the level of phosphorylation of the exchanger molecules, which can also affect their intrinsic turnover rate.
Results
Imaging and analysis of pH-dependent HPTS fluorescence inside the sealed t-system of muscle fibers
Fig. 3 shows the confocal fluorescence image emitted from HPTS trapped in the t-system of a skinned fiber when excited at 488 nm. As expected, the typical double-banded striated pattern of the mammalian t-system could be seen, showing that HPTS was trapped in the sealed t-system. Spatially averaged HPTS fluorescence signals were recorded only from fiber regions where transverse tubules could be clearly seen and for which the surface area/volume ratio (SAt/Vt) has been previously determined as described in Materials and methods. This was done to enable calculation of the t-system membrane permeability to H+, after abrupt changes in the cytoplasmic pH, [Na+], and resting membrane potential as described in the section The proton permeability coefficient of the t-system membrane.
Figure 3.
HPTS fluorescence signal from the t-system of a rat skinned fiber. HPTS was trapped in the skinned fiber as described in Materials and methods. The long axis of the fiber was positioned to run in parallel with that of the image. Note that continuous imaging of the t-system in this manner allowed sampling of the proton-dependent changes in HPTS fluorescence from more than one hundred planes of transverse tubules. Inset: Magnified region of the preparation showing the structure of the t-system.
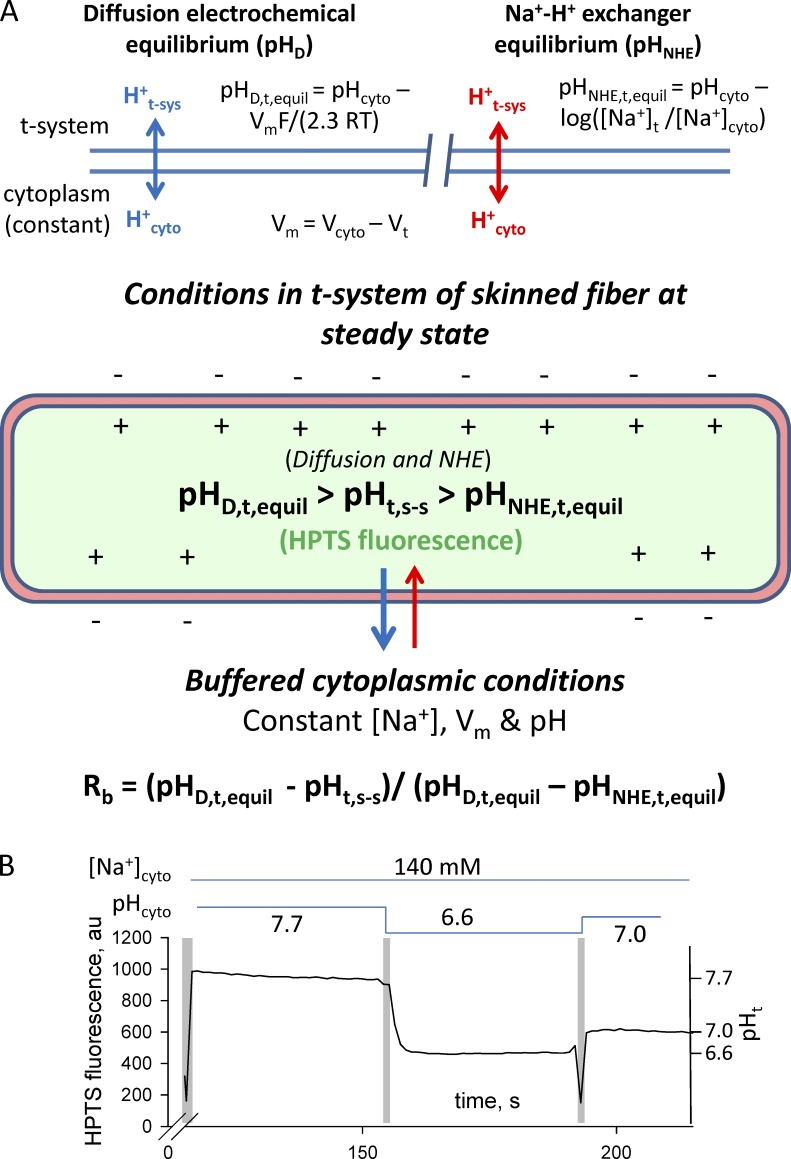
In the total absence of bicarbonate and lactate in our solutions, protons move across the t-system membranes by passive diffusion down an electrochemical gradient, an NHE system, or both, as illustrated in Fig. 4. Consequently, the pH in the sealed t-system will be at steady state, when proton fluxes via the NHE system and passive diffusion down the electrochemical gradient cancel out, or when both the NHE system and proton diffusion are at thermodynamic equilibrium.
Figure 4.
Fluxes that determine sealed t-system pH at steady state (pHt,s-s) and pH calibration of the HPTS signal. (A and B) Diagram of proton fluxes across the t-system membrane in skinned muscle fibers (A) and calibration of HPTS signal inside the sealed t-system using monensin (B). The schematic diagram indicates the expected movements of protons across a membrane caused by diffusion (top, left) and caused by the action of NHE (top, right). The diagram of the sealed t-system labeled in green shows that the HPTS trapped in the sealed t-system will report the pH in the t-system at steady state when there is no net flux of protons across the t-system caused by diffusion and NHE activity. The fluorescence traces in B show a typical pH calibration of HPTS fluorescence inside the sealed t-system. Solution exchanges are indicated by the vertical pale gray bars, and the composition of the cytosolic solution is indicated by the horizontal lines above the trace. Note that monensin was applied in the first indicated solution. The HPTS fluorescence signal has been used to calculate the FMax, pK, and background of 889, 7.31, and 315 arbitrary units (au), respectively. The calibrated t-system pH (pHt) is indicated on the right y axis. pHD,t,equil, pH in the t-system at electrochemical equilibrium; pHNHE,t,equil, pH in the t-system at NHE equilibrium; pHt,s-s, pH in the t-system at steady state.
In this study, we used two types of pH buffered cytosolic solutions: K-based solutions similar in composition to the myoplasmic environment in the resting fiber with respect to ATP, creatine phosphate, Mg2+, K+, Na+, and divalent anions, and Na-based solutions in which all potassium ions were replaced by sodium ions (see Materials and methods).
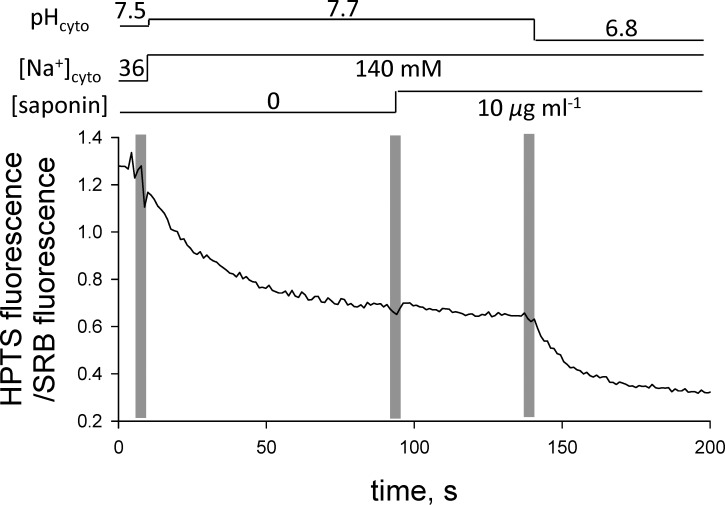
According to the many studies conducted in our laboratories on rat EDL mechanically skinned fibers, the t-system membrane is fully depolarized (i.e., Vm ≈ 0 mV) in the Na-based solutions without any potassium present (Lamb et al., 1992; Lamb and Stephenson, 1994; Posterino et al., 2000; Ørtenblad and Stephenson, 2003; Nielsen et al., 2004; Pedersen et al., 2004; Stephenson, 2006). We also present direct evidence that the membrane potential in Na-based solution is close to 0 mV, because there is no change in tubular pH when the t-system membrane is perforated by saponin (Launikonis and Stephenson, 1999) after the preparation is equilibrated in Na-based solutions (Fig. 5). If the t-system membrane potential were different from 0 mV in the Na-based solution, then the pH in the t-system would suddenly change upon exposure to saponin, as the pH buffer from the Na-based solution would diffuse into tubular space and the fluorescent dye (HPTS) would diffuse into the bathing solution.
Figure 5.
Addition of saponin to the depolarized t-system has little effect on the fluorescence signal. Saponin (10 µg/ml) causes small perforations (pores) in the t-system membrane and rapid equilibration of the pH in the t-system lumen with that in the cytosolic environment. In this experiment, the t-system was loaded with an additional fluorescent probe that is not sensitive to pH (SRB, see Materials and methods) to correct for the loss of HTPS signal associated with the diffusion of HTPS from the t-system lumen through the pores made by saponin. Accordingly, the fluorescence signal is shown as the ratio between the HTPS and SRB fluorescence. Solution exchanges are indicated by the vertical pale bars, and the composition of the internal solution is indicated by the horizontal lines above the trace.
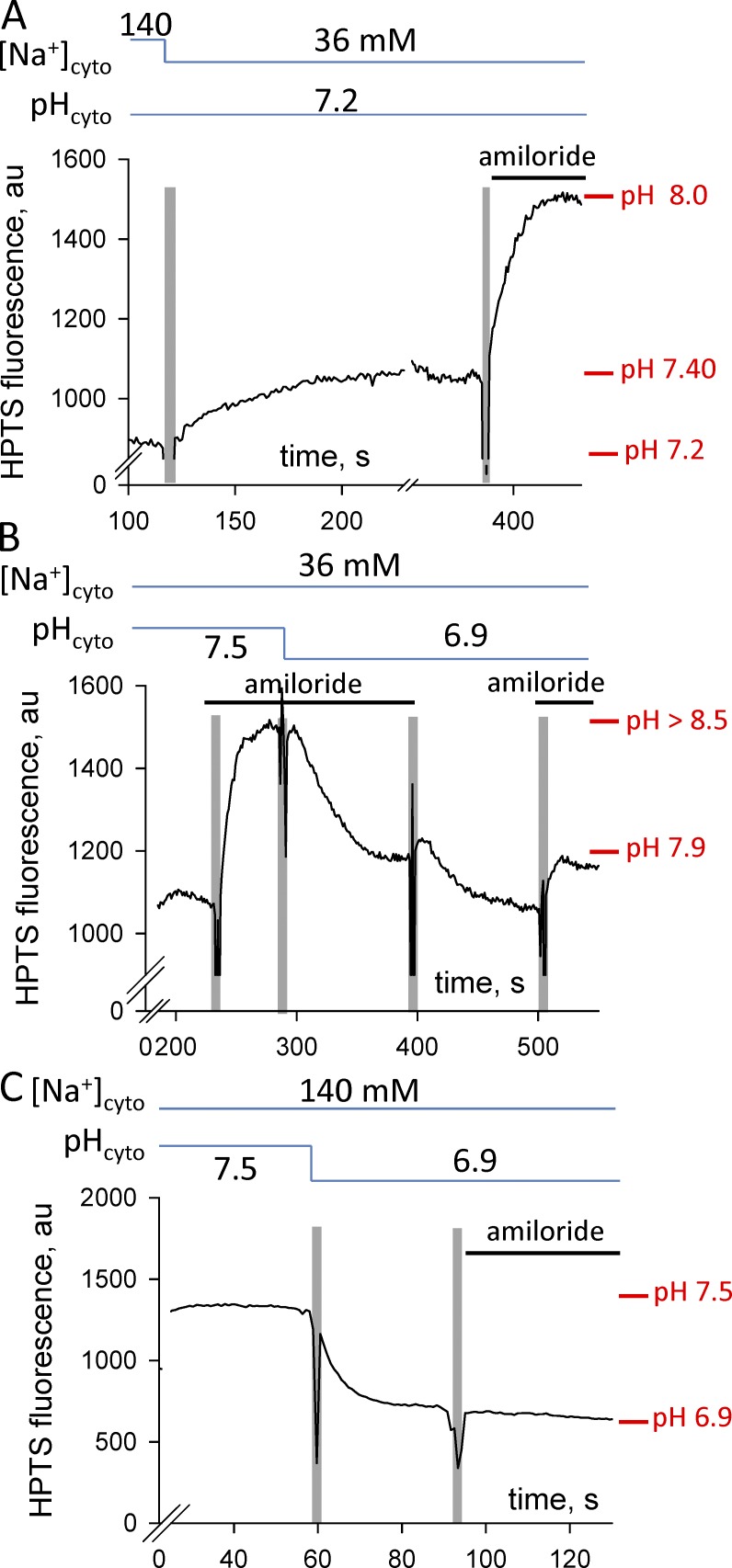
In contrast, placing the skinned fiber with the sealed t-system into the K-based cytosolic solutions causes the t-system membrane to become normally polarized (lumen of the t-system more positive than the K-based cytosolic solution) under the action of the Na+/K+ pump, as we have previously shown (Lamb et al., 1992; Lamb and Stephenson, 1994; Posterino et al., 2000; Ørtenblad and Stephenson, 2003; Nielsen et al., 2004; Pedersen et al., 2004; Stephenson, 2006). The level of polarization of the sealed t-system in skinned fast-twitch fibers of the rat bathed in K-based solutions permits the generation of propagated action potentials when electrically stimulated (Edwards et al., 2012). This indicates that the membrane potential across the t-system membrane (Vm) in our preparation is less than −75 mV; otherwise, Na+ channels would inactivate and would not be able to support propagated action potentials. (Direct evidence that the sealed t-system is well polarized in the K-based solutions used in this study is also shown in Fig. 6 B, where the proton concentration in the lumen of the sealed t-system is one pH unit greater than that in the K-based solutions when the NHE system is partially blocked by amiloride, indicating that Vm < −60 mV.)
Figure 6.
Amiloride effects on the pHt. Traces of t-system trapped HPTS fluorescence signal. (A) Changes in the pHt after replacement of Na-based solution of pH 7.2 with K-based solution of pH 7.2 and after the introduction of 50 µM amiloride. (B) The effect of amiloride on the pHt in K-based solutions is reversible. (C) The HPTS fluorescence signal does not change after the introduction of amiloride to the Na-based solution in which the preparation was equilibrated. Solution exchanges are indicated by the vertical pale bars, and the composition of the internal solution is indicated by the horizontal lines above each trace. The presence of amiloride in solutions is indicated as a solid bar just above the trace.
The polarization of the t-system when mechanically skinned fibers are transferred from Na-based to K-based solutions opposes the diffusion of protons from the cytosolic solution into the t-system lumen and enhances the proton diffusion from the t-system lumen to the cytosolic solution. In contrast, the reduction of [Na+] ([Na+]cyto) from 139–142 mM (depending on pH) in Na-based cytosolic solutions to 36 mM in the K-based cytosolic solutions increases the net proton flux into the t-system lumen via the NHE-system. The pH in the t-system lumen reaches steady state when the net proton fluxes across the t-system membrane balance out as shown diagrammatically in Fig. 4. At steady state, the pH in the sealed t-system (pHt,s-s) lies between the diffusion equilibrium pH (pHD,t,equil = pHcyto − (VmF/2.3RT), where Vm is the membrane potential, F is the Faraday number, R is the universal gas constant, and T is the absolute temperature such that 2.3 RT/F = 59 mV at 23°C) and the NHE equilibrium pH (pHNHE,t,equil = pHcyto − log([Na+]t/[Na+]cyto). Note that an increase in the net proton flux from the cytosolic solution to the t-system lumen via the NHE-system causes a decrease in t-system pH, whereas a decrease in the net proton flux makes the t-system lumen more alkaline.
The value of the index Rb (0 < Rb < 1.0) defined by Eq. 16 highlights the relative importance of the two systems for determining the steady-state pH in the sealed t-system. An Rb value closer to 0 indicates that diffusional proton fluxes are the predominant controlling factor; an Rb value closer to 1 signifies that NHE proton fluxes are the predominant factor, whereas a value close to 0.5 indicates that both systems play an important role in controlling the pH difference across the t-system membrane:
| (16) |
Fig. 6 A shows an example in which changing the cytosolic solution from a Na-based solution of pH 7.2 to a K-based solution of pH 7.2 (when a membrane potential more negative than approximately −75 mV develops) causes the pH in the sealed t-system to rise from 7.2 to 7.4. For Vm = −75 mV, this corresponds to Rb = 0.56. In the absence of an NHE system in the t-system membrane, the pH in the t-system would have been expected to increase by >1.27 pH units (i.e., to pH >8.47) for protons across the membrane to be at equilibrium (pHD,t,equil > pHcyto +75 mV/59 mV) and for Rb to approach 0. The Rb value for 10 fibers equilibrated in K-based solutions was 0.43 ± 0.05 (Table 1), indicating the presence of functional sodium-proton exchanger molecules in the t-system membrane, which play an important role in controlling the pH difference across the t-system. Note that the Rb values varied considerably between individual fibers: the lowest value recorded for one fiber was 0.16, and the highest value recorded for another fiber was 0.57 (Table 1). This shows that the NHE system is functionally different between different muscle fibers.
Table 1. General properties of the t-system membrane in relation to proton movements across it via diffusional fluxes and sodium-proton exchanger system.
| Property | Mean ± SEM | n | Range |
|---|---|---|---|
| Index Rb reflecting the relative importance of diffusional and NHE proton fluxes in determining the pH difference across the membrane at steady state | 0.430 ± 0.045 | 10 | 0.16 to 0.57 |
| Proton permeability coefficient PH (×10−4 m/s) | 1.58 ± 0.30 | 7 | 0.33 to 2.79 |
| Sodium-proton exchanger density CNHE (pmol/m2) | 339 ± 116 | 7 | 5 to 800 |
Furthermore, as shown in Fig. 6 A, application of the NHE blocker amiloride (50 µM) to the K-based solution caused a marked pH rise from 7.4 to 8.0 and a decrease in Rb value from 0.56 to 0.25, confirming the presence of a functional endogenous NHE system in the t-system membranes of skeletal muscle. Similarly, as shown in Fig. 6 B, application of 50 µM amiloride to pH-7.5 and -6.9 K-based solutions caused the rise of t-system pH. On average, application of 50 µM amiloride to K-based solutions of pH 6.8, 7.2, and 7.5 caused alkalinization of the t-system by 0.69 ± 0.23 pH units (n = 5).
Note that amiloride did not change the t-system pH when the fiber was equilibrated in a Na-based solution (Fig. 6 C); this lack of effect is consistent with the pH across the t-system membrane being in equilibrium, as we show in the next section of the Results. The amiloride effect was largely reversible, as shown in Fig. 6 B, by the acidification of the t-system when amiloride was removed from the pH-6.9 K-based solution and the subsequent rise of pH to similar levels when amiloride was reintroduced in the solution.
T-system pH in Na-based cytosolic solutions
The steady t-system pH level in Na-based solutions of different pH was assessed from fluorescent intensity measurements on the same individual fibers before and after treatment with monensin. As indicated in Materials and methods, monensin acts as a proton-sodium exchanger (Mollenhauer et al., 1990) such that in its presence, at equilibrium, the ratio between Na+ concentrations across the t-system membrane equals the ratio between proton concentrations across the membrane:
| (17) |
Fig. 7 shows a representative example of the spatially averaged HPTS fluorescence signal in a skinned fiber preparation after rapid changes of cytosolic solutions before and after exposure to 20 µM monensin. In the fluorescence intensity trace, the HPTS fluorescence signal changed little after monensin was applied in the pH-7.0 Na-based solution. This is consistent with the presence of an endogenous NHE system in the t-system that caused pH equilibration across the t-system membrane before the addition of monensin, because the pH in the t-system would not change when the concentration of exchanger molecules in the membrane rises (i.e., monensin) if the system were already at equilibrium. Furthermore, because the sodium concentration in the HPTS external solution in the lumen of the t-system is in the order of 150 mM and similar to the sodium concentration in the Na-based cytosolic solutions (139–142 mM), it follows that the pH in the lumen of the t-system must be close to the pH of the Na-based cytosolic solution before and after treatment with monensin. Additional support for the proposition that the pH in the sealed t-system reaches equilibrium with cytosolic pH in Na-based solutions is given by the observation that amiloride had no effect on the pHt when it was applied after equilibration of the preparation in a Na-based cytosolic solution as shown in Fig. 6 C.
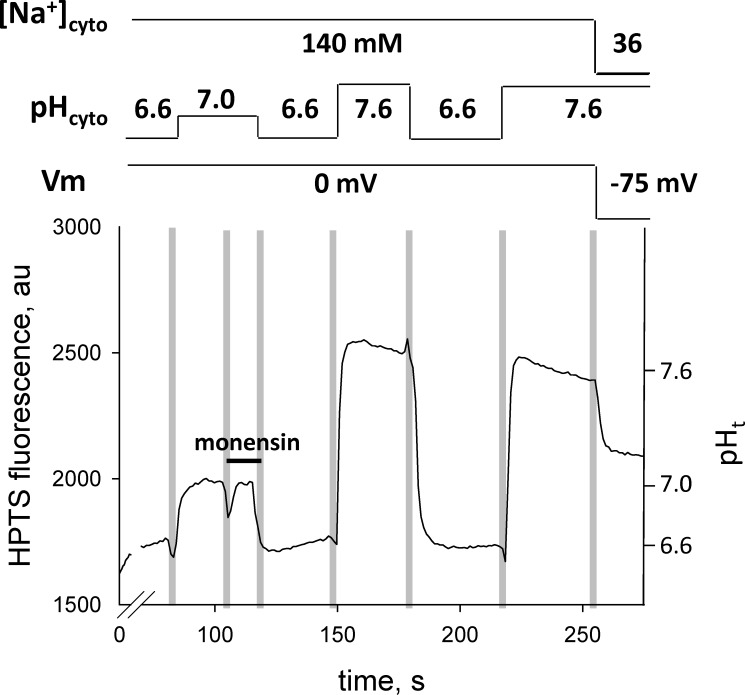
Figure 7.
Monensin effects on the pHt. Application of 20 µM monensin to Na-based cytosolic solutions causes little change in the HPTS signal. After exposure to monensin, the HPTS fluorescence signals in three Na-based cytosolic solutions of different pH, where the t-system is depolarized, were used to calibrate the pH in the t-system. The decrease in pHt at the end of the trace after the exchange of the Na-based solution with the K-based polarizing solution of the same pH causes a decrease in the HPTS signal, indicating that monensin was incorporated into the t-system membrane as described in the text. Solution exchanges are indicated by the vertical pale bars, and the composition of the internal solution is indicated by the horizontal lines above the trace.
To prove that monensin was incorporated and functional in the t-system membrane, at the end of the experiment shown in Fig. 7, the preparation was transferred from the Na-based cytosolic solution of pH 7.6 containing 142 mM Na+ to the polarizing, K-based cytosolic solution of same pH containing 36 mM Na. In the absence of monensin, the luminal t-system pH rises when the preparation is transferred from Na-based to K-based polarizing solutions of the same pH, as shown in Fig. 6 A, because the net proton flux into the t-system via the endogenous NHE system is smaller than the proton flux out of the t-system by diffusion, caused by membrane polarization. In contrast, the lumen of the t-system became more acidic (pH 7.1) after monensin treatment when the Na-based cytosolic solution was replaced by the K-based polarizing solution, as shown in Fig. 7. This was possible only if monensin had been incorporated in the t-system such that the net proton flux into the t-system lumen via the combined NHE system (endogenous and monensin-based) was now greater than the proton flux in the opposite direction caused by membrane polarization when the Na-based cytosolic solution was replaced by the K-based polarizing solution of the same pH. Note that after the monensin treatment, the Rb value in the pH-7.6 K-based solution was 0.94, indicating that the pH in the sealed t-system was effectively controlled by the NHE system.
As described in Materials and methods, the pKHPTS value, the maximum HPTS-emitted fluorescence intensity, Fmax, and the background fluorescence, B, were determined for individual fibers after measuring the fluorescence intensities in three Na-based solutions of different pH after monensin treatment. The parameters determined in this way for each fiber were then used to determine the steady pH levels in Na-based (and K-based) solutions from the fluorescence intensities measured in the same fiber before exposure to monensin using Eq. 4. In Eq. 4, F1 is the fluorescence intensity in a given Na-based (or K-based) cytosolic solution minus background, B, and similarly, F is the fluorescence intensity minus B in the Na-based (or K-based) solution for which the pH is to be determined.
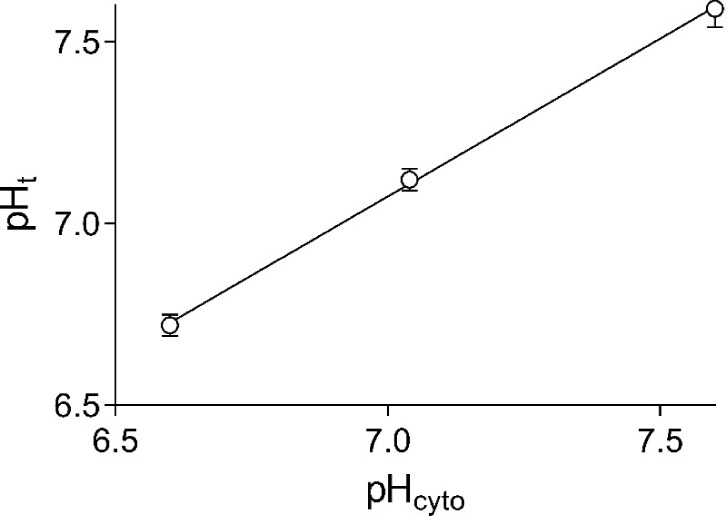
Results obtained with 10 fibers equilibrated in Na-based solutions of pH 6.60, 7.04, and 7.60 before exposure to monensin are shown in Fig. 8. The pH values in the sealed t-system are close to the pH values of the cytosolic solutions, and the data points are very well fitted by a straight line. The tight correlation between tubular and cytosolic pH in Na-based solutions permitted the use of this linear relationship to calibrate HPTS fluorescence signals in preparations without exposure to monensin. For such calibration, the preparations were equilibrated in three Na-based cytosolic solutions of different pH, and Eq. 5 was used to determine the pKHPTS value, the maximum HPTS-emitted fluorescence intensity, Fmax, and the background fluorescence, B, for each individual fiber. As mentioned in Materials and methods, it was important to avoid contamination of freshly dissected fibers with monensin, which does not easily wash out. Therefore, experimental chambers were discarded after they were exposed to monensin.
Figure 8.
The steady-state relationship between pHt and pHcyto in Na-based solutions. Data are displayed as mean ± SEM. Results from 10 fibers.
Qualitative observations proving the same point—namely, that the pH in the t-system is very close to the pH in Na-based cytosolic solutions—were made on three preparations, in which saponin was used to induce the formation of pores in the t-system membrane (Launikonis and Stephenson, 1999). Skinned fibers with sealed t-system loaded with HTPS and SRB were first equilibrated in a Na-based cytosolic solution and then exposed to the same solution containing in addition 10 µg/ml saponin, which is known to perforate the t-system (Launikonis and Stephenson, 1999). From the result shown in Fig. 5, the ratio between the HPTS and the SRB fluorescence signals remained constant for 50 s after the cytosolic Na-based solution of pH 7.7 was replaced with the same solution that additionally contained 10 µg/ml saponin. This indicates that the pH in the sealed t-system must have been very close to the pH value (7.7) in the cytosolic solution, in full agreement with the results in Fig. 5.
T-system pH in K-based cytosolic solutions
Fig. 9 A shows the steady-state t-system pH in the lumen of the sealed t-system measured in fibers equilibrated in K-based cytosolic solutions of different pH. On average, the pH in the t-system was more alkaline by 0.46 ± 0.09 pH units (n = 10 fibers) than that of the polarizing K-based cytosolic solutions. A major factor contributing to the relatively large scatter between the data points is the variation of the NHE system activity between different fibers. The scatter is greatly reduced when measurements are made on the same fibers in different K-based solutions, as shown in Fig. 9 B.
At steady state, the NHE proton flux (ΦH-NHE) balances the diffusional proton flux such that
| (18) |
The diffusional proton flux when protons move down their electrochemical gradient () is given by the constant field equation:
| (19) |
where is the membrane permeability coefficient for protons and ζ = Vm F/RT. The proton flux is positive from the cytosolic solution to t-system lumen and negative from t-system lumen to cytosolic solution. For our conditions, T = 296 K, ζ = −2.94 for Vm = −75 mV, and ΦH-NHE is given by the following expression:
| (20) |
Fig. 9 C displays the predicted ΦH-NHE proton fluxes at pHcyto 6.8, 7.2, and 7.5 derived from data shown in Fig. 9 B using Eq. 20. The fluxes were normalized with reference to the flux in the K-based 6.8 pHcyto solution in a particular fiber. The marked decline of the normalized ΦH-NHE flux derived from our measurements as the pHcyto rises from 6.8 to 7.5 (Fig. 9 C) is remarkably well accounted for by the eight-state ping-pong-type NHE model developed by Cha et al. (2009) to fit a variety of NHE experimental data in cardiac myocytes, as discussed in Materials and methods. The solid curve in Fig. 9 C shows the normalized NHE proton fluxes at pHcyto 6.8–7.5 calculated from the NHE model using the same set of parameters as derived by Cha et al. (2009) for cardiac myocytes, except for the dissociation constant KM-cyto in the proton-modifier component, which was 14.8 nM instead of 30.7 nM.
Because the temperature in our experiments was 23°C, whereas the rate constant parameters in the model of Cha et al. (2009) were obtained based on experiments conducted at 37°C, we use a nominal factor f (>2) to divide the turnover rate (JH-exch ∙ Mod) calculated from the model to yield the NHE proton fluxes at 23°C:
| (21) |
where CNHE is the exchanger concentration in the t-system membrane in mol/m2, and the turnover rate (at 37°C; JH-exch ∙ Mod) is expressed in s−1. The mean value of the ΦH-NHE flux in the K-based pHcyto 6.8 solution was 296 (± 22) s−1∙(CNHE/f).
The close fit (Fig. 9 C) between the NHE proton fluxes predicted from diffusional proton fluxes described by Eqs. 18 and 20 (open circles in Fig. 9 C) and the NHE model described by Eqs. 13, 14, 15, and 21 (closed circles and solid line) permits us to link Eqs. 20 and 21:
| (22) |
where JH-exch ∙ Mod is calculated from the NHE model in Materials and methods for the prevalent pH and Na+ concentrations in the cytosol and t-system.
The proton permeability coefficient of the t-system membrane
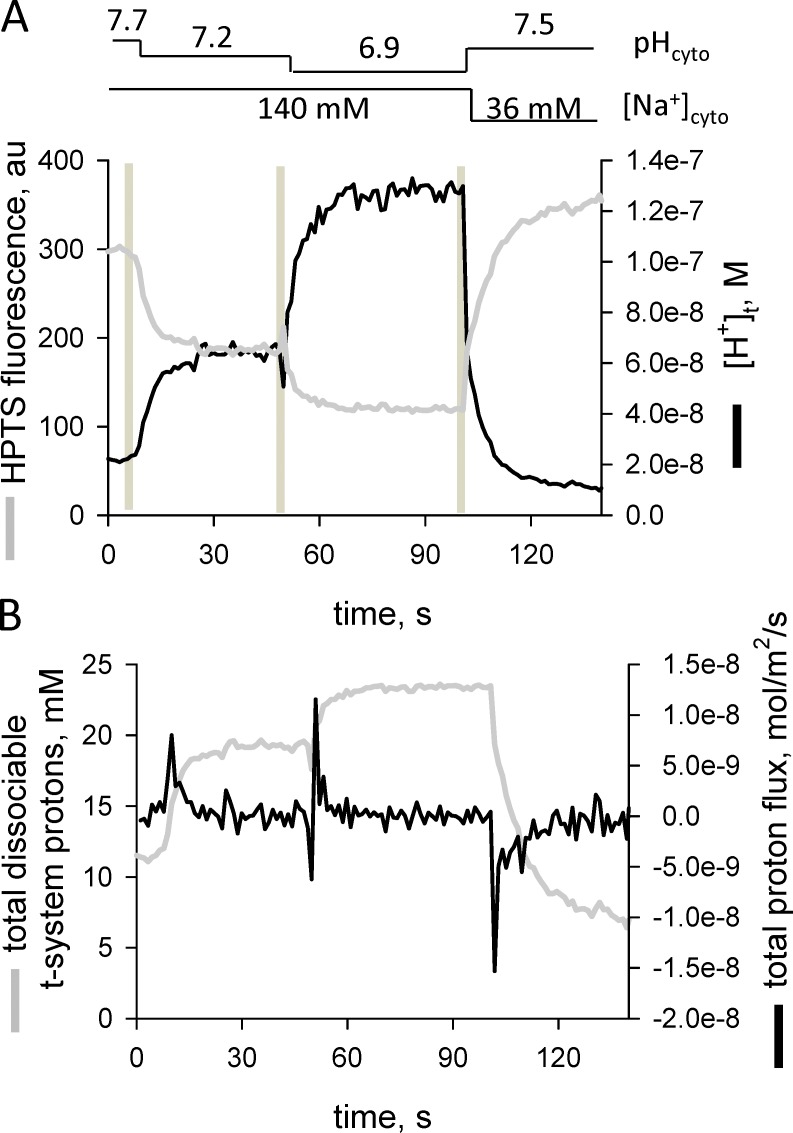
Fig. 10 shows a representative example of HTPS fluorescence changes in the sealed t-system together with the associated pH changes and proton fluxes across the t-system membrane when the preparation was transferred between a series of solutions. The magnitude of the proton flux (positive or negative) is greatest immediately after the preparation is transferred from one cytosolic solution to another. Absolute proton fluxes occurring across the t-system membranes upon preparation transfer between cytosolic solutions are obtained using Eq. 11 as discussed in Materials and methods.
Figure 10.
Proton fluxes across the t-system after rapid changes in cytoplasmic pH and membrane potential. In Na+-based internal solutions, the pH was changed from 7.7 to 7.2 to 6.9 and then changed to a K+-based solution with a pH of 7.5 while continuously imaging the t-system HPTS fluorescence signal. The spatially averaged profile shows a stepwise decrease in t-system pH with each drop in cytoplasmic pH in Na+ solution. The final solution substitution was to a pH-7.5 K+-based internal solution, which polarizes the t-system. (A) Fluorescence intensity and derived proton concentration ([H+]t) changes in the sealed t-system. (B) Changes in total dissociable proton concentration in the sealed t-system and proton fluxes across the sealed t-system membrane.
Two independent methods were used to evaluate the proton permeability coefficient () across the t-system membrane. The first method was designed to minimize the NHE proton flux component and maximize the diffusional flux component when changing solutions. For this purpose, fibers were first equilibrated in the Na-based cytosolic solution of pH 6.9 containing 140 mM Na+, and then the cytosolic solution was rapidly changed to a K-based solution of pH 7.6 containing only 36 mM Na+. At the time of the solution change, the t-system was fully depolarized and the pHt was in equilibrium with the pHcyto and close to pH 6.9, as shown in Fig. 8. Because the ratio between the Na+ and proton concentrations in the cytosolic solutions remained constant when the solutions were swapped (140 mM Na+/10−6.9 H+ ≈ 36 mM Na+/10−7.5 H+), the NHE-proton flux component across the t-system stayed in equilibrium (Eq. 17) and was close to zero immediately after the solution change took place. Thus, the peak proton flux occurring immediately after the solution change was entirely caused by proton diffusion out of the t-system according to the following expression:
| (23) |
For the fiber shown in Fig. 10, the observed peak proton flux under these conditions was −14.4 nmol/m2/s, which corresponds to a permeability coefficient of 0.000152 m/s (−14.4 × 10−9 mol/m2/s/−9.42 × 10−5 mol/m3). The mean value thus measured in three fibers was 1.81 ± 0.72 × 10−4 m/s.
The second method used to evaluate the permeability coefficient of the t-system membrane for protons involved transfer of the preparation from a Na-based cytosolic solution to another Na-based cytosolic solution of different pH. In this situation, there is a net proton diffusion flux as well as a net ΦH-NHE flux between the cytosol and the lumen of the t-system.
Because the t-system is fully depolarized in the Na-based solutions, the diffusional proton flux across the t-system membranes in the Na-based solutions is described by the following equation:
| (24) |
The ΦH-NHE flux component () can also be expressed as a function of using Eq. 22 such that
| (25) |
For example, when a preparation is transferred from the pH-7.5 Na-based solution (after steady state is reached and pHt is close to pHcyto, as shown in Fig. 8) to the pH-7.1 Na-based solution, the peak magnitude of NHE proton flux occurs immediately after solution change when pHt ≈ 7.5, pHcyto 7.1, [Na+]t = 150 mM, and [Na+]cyto =140 mM. Using Eqs. 12, 13, 14, and 15 in Materials and methods for this situation, ΦH-NHE = (CNHE/f)·32.5 s−1.
For the fiber used in the experiment shown in Fig. 10, the CNHE/f value () obtained from pH measurements at steady state in the pH-7.5 cytosolic K-based solution was 690 nmol/m3/s. Therefore, the peak NHE proton flux () when transferring the preparation from the pH-7.5 Na-based to the pH-7.1 Na-based solution was 32.5 s−1·690 nmol/m3/s = ·22.4 µmol/m3, and the peak amplitude of the total proton flux () was
| (26) |
Note that the NHE proton flux is generally smaller than the diffusional proton flux after transfer between Na-based cytosolic solutions.
Because according to Fig. 10, the peak absolute proton flux was 7.94 nmol/m2/s after the transfer from the pH-7.5 to the pH-7.1 Na-based solution, the proton permeability coefficient for this fiber was 0.000113 m/s (7.94 nmol/m2/s/70.2 µmol/m3). The mean proton permeability coefficient obtained with this second method on seven fibers was 1.58 ± 0.30 × 10−4 m/s, as shown in Table 1.
Density of NHE molecules in the t-system membrane
The density of exchanger molecules in the t-system membrane (CNHE) was estimated from the value of CNHE/f determined according to Eq. 22 based on the value of (measured in the respective fiber) and pHt measurements at steady state in cytosolic K-based solutions of pHcyto in the range 6.8–7.5 in the same fiber. For the fiber used in Fig. 10, the CNHE/f value was 77.9 pmol/m2 t-system membrane, whereas the mean value for seven fibers was 129 ± 44 pmol/m2. It is important to point out that phosphorylation of the NHE molecules can also alter their intrinsic catalytic activity. Consequently, the turnover of the exchanger molecules depends not only on temperature but also on the phosphorylation status of the exchanger molecules. If we assume a constant level of exchanger phosphorylation after the fiber was skinned and use f = 2.63 to account for a temperature-dependent change in the turnover rate from 37°C and 23°C with a temperature coefficient Q10 = 2, then the mean density of exchanger molecules in the t-system membrane of rat EDL fibers would be CNHE = (129 ± 44) × 2.63 = 339 ± 116 pmol/m2.
Discussion
This study allowed characterization of diffusional and NHE proton fluxes across the sealed t-system of fast-twitch mammalian skeletal muscle fibers. All fibers analyzed in this study were of fast-twitch type, because the presence of BTS in the cytosolic solutions selectively prevented contraction of fast-twitch fibers only; slow-twitch fibers would have contracted in the presence of BTS and pulled out of the clamps upon transfer between K-based to Na-based solutions, when the t-system rapidly depolarized and Ca2+ was released from the SR. Moreover, the NHE proton fluxes described in this study are likely to be mediated by the NHE1 isoform of the sodium-proton exchanger because NHE1 is the predominant isoform in fast-twitch skeletal muscle (Juel, 2000, 2008).
The t-system was loaded with a solution containing 10 mM of the membrane-impermeant pH-sensitive dye HPTS, which also acts as a pH buffer, and 20 mM of the membrane-impermeant pH buffer HEPES to increase the pH-buffering capacity of the t-system content and enable accurate measurements of proton fluxes across the t-system membrane. The t-system was then sealed when the surface membrane was peeled off by microdissection under paraffin oil, a procedure known as mechanical skinning.
Collectively, the results show that the t-system of fast-twitch mammalian skeletal muscle fibers contains an endogenous NHE exchange system that removes protons from the cytosolic side against a sodium gradient. Unlike the NHE exchanger in red blood cells, which is inhibited by amiloride only when applied on the external side of the plasma membrane (Grinstein and Smith, 1987), the NHE exchanger in the t-system was also reversibly inhibited when amiloride (50 µM) was applied on the cytosolic side (Fig. 6), where NHE1 was shown to have a high-affinity binding site for amiloride (Desir et al., 1991).
The proton permeability coefficient of the t-system membrane
The proton permeability coefficient PH of the t-system has been evaluated using two independent methods described in detail in Results. The two methods produced similar mean values that were not significantly different from each other: 1.81 ± 0.72 × 10−4 m/s using the first method and 1.58 ± 0.30 × 10−4 m/s using the second method. The close set of values obtained with the two independent methods adds strength to the soundness of the results.
Proton permeability coefficients of 1.3 × 10−4 m/s and 10−5 m/s were measured for 3.1- and 3.6-nm-thick phosphatidylcholine lipid bilayers (thickness of the hydrophobic region of the bilayers 2.0 and 2.5 nm, respectively; Paula et al., 1996). The dominant mechanism for proton permeation in these lipid bilayers is via pore formation/water wires in the bilayer produced by thermal fluctuations (Paula et al., 1996). The bilayer thickness in plasma membranes of mammalian cells is ∼3.6 nm, and the presence of diverse membrane proteins (Mitra et al., 2004) or lipid rafts (Gensure et al., 2006) can alter the bilayer properties such as to make it more prone to the formation of transient pores/water wires produced by thermal fluctuations and thus increase the proton permeability coefficient.
The value of the proton permeability coefficient determined with the second method is not very sensitive to the value of the membrane potential across the t-system: it decreases by only 5% when the membrane potential is changed from −75 to −90 mV. However, the value of the proton permeability coefficient calculated with either method is sensitive to the volume-to-surface area of the sealed t-system (Vt/SAt), as the measured proton fluxes used to determine the permeability coefficient are proportional to this parameter according to Eq. 10. In our calculations, we used a fixed value of 4.1 nm for the rat EDL muscle fibers as discussed in Materials and methods based on data reported by Dulhunty (1984). However, as pointed out by Dulhunty (1984), there are uncertainties in assigning a precise Vt/SAt value to individual muscle fibers, which explains the relatively large variation of the estimated proton permeability coefficient between fibers (range between 3.3 × 10−5 and 2.8 × 10−4 m/s as shown in Table 1).
A proton permeability coefficient of 10−5 m/s was previously reported for the frog sartorius muscle fibers as an underestimate of the true permeability coefficient (Izutsu, 1972). The author was aware that in that case, there was a proton flux in the opposite direction of the passive diffusional flux, which, if taken into consideration, would have markedly increased the estimated value of the permeability coefficient. However, little was known at the time about the presence of a sodium-proton exchanger in muscle and the magnitude of the proton flux associated with it.
Note that a proton permeability coefficient PH =2 × 10−4 m/s for the t-system membrane would contribute little (<2 mV) to the resting membrane potential under physiological conditions (external pH 7.40) if the contribution of the proton component PH ∙ [H+]t (2 × 10−4 × 10−7.4 = 8 × 10−12 m/s per mol/L) to the value of the numerator in the Goldman–Hodgkin–Katz equation for the t-system membrane was 8% or less of the combined contribution of external Na+ (150 mM) and K+ (4 mM) and internal Cl− (∼4.5 mM). In such a case, the combined contribution of external K+, external Na+, and intracellular Cl− must be >10−10 m/s per mol/L.
Experiments on intact rat skeletal muscle in vivo (Carter et al., 1967) imply the presence of a large proton permeability coefficient of the plasma membrane (that includes the t-system) to produce the observed fast responses of intracellular pH to changes of extracellular pH. Note that Carter et al. (1967) used castor oil to cover the surface of the muscle exposed to experimentation, and that castor oil had been later shown to be a potent inhibitor of the sodium-proton exchanger (Tiruppathi et al., 1988). This latter observation explains in full why the carefully conducted experiments of Carter et al. (1967) showed that the intracellular proton concentration was (in that case) effectively in electrochemical equilibrium with extracellular proton concentration. The results of Carter and colleagues fueled a major controversy at that time that lasted for many years regarding the mechanism of intracellular pH regulation in muscle.
The primary pH buffer in mammals is the CO2/HCO3− buffer system, in which CO2 freely diffuses across membranes and acts as a membrane-permeant acid equivalent, whereas HCO3− is a membrane-impermeant base that crosses the membrane only with the help of bicarbonate transporters such as NCB and anion exchangers such as the Cl−/HCO3− exchanger. Monocarboxylate transporters and Ca2+ transporters can further influence the net proton flux. The results of Carter et al. (1967) showed that protons effectively distribute across the plasma membrane of relaxed muscle in vivo in accord with the Nernst equation when the NHE fluxes are inhibited. Although all other physiological proton buffering systems are functional (NCB, anion exchangers, monocarboxylate transporters, etc.), it follows that the NHE fluxes are the key contributors to the more alkaline cytosolic pH in resting muscle than that corresponding to the proton equilibrium potential.
The NHE exchange system
The NHE system in the t-system of rat fast-twitch muscle fibers can balance the diffusional proton fluxes across the t-system membrane to reach a steady state between the pH in the lumen of the t-system and the cytosolic pH in a matter of seconds.
The exchanger activity was highest at 6.8 cytosolic pH and declined sharply at cytoplasmic pH values >7.2 (Fig. 9 C). The decline was steeper than could be accounted for by a simple ion-exchange mechanism, indicating the presence of a proton-modifier component (Mod) as initially proposed by Aronson (1985), where the NHE exchanger has an additional intracellular proton binding site that needs to be occupied for the exchanger’s activation. The proton modifier component allows regulation of the NHE exchanger by intracellular pH.
The eight-state ping-pong-type NHE model developed by Cha et al. (2009) to fit a variety of NHE experimental data in cardiac myocytes also fitted the predicted pH-dependence of the NHE-system activity in skeletal muscle remarkably well (Fig. 9 C). The model consists of the ion-exchange component and the modifier component. The ion-exchange component of the NHE system in fast-twitch skeletal muscle was well fitted using the same parameter values as for cardiac myocytes; the proton dissociation constant on the modifier component for skeletal muscle was, however, only half that used for cardiac myocytes (14.8 vs. 30.3 nM). The NHE model of Cha et al. (2009) was adopted for the quantitative description of NHE activity under different cytosolic and luminal t-system conditions with respect to [Na+] and pH. A nominal factor f was introduced to adjust the exchanger’s turnover rate at different temperatures and different levels of phosphorylation.
For the calculation of the exchanger density in the t-system membrane (CNHE = 339 ± 116 pmol/m2; Table 1), we used f = 2.63 to account for a temperature-dependent change in the turnover rate from 37°C and 23°C. Using Avogadro’s number (6.022 × 1023 exchanger molecules/mol−), the mean NHE exchanger density corresponds to 203 exchanger molecules/µm2 of t-system membrane. Because the perimeter of the t-tubules in rat fibers is ∼0.147 nm (Dulhunty, 1984), the surface area of a tubule surrounding one myofibril of 1-µm length is ∼0.15 µm2 (0.147 µm × 1 µm), and the mean number of exchanger molecules per tubule surrounding one myofibril is ∼30.
The 150-fold variation in the NHE density (in Table 1) is one order of magnitude greater than the variation of calculated proton permeability coefficient. The variation of the permeability coefficient is most likely caused by different values in the volume-to-surface area ratio between fibers rather than to real differences in proton permeability coefficients between fibers, as discussed in the previous section. The much greater variation in the CNHE value between fibers most likely reflects true differences in either exchanger density between fibers or transport activity reflected in the value of the factor f. Indeed, it is known that hormones can alter the phosphorylation state, which in turn modulates the transport activity of the NHE1 exchangers (Putney et al., 2002), and that NHE1 exchangers can be translocated to the plasma membrane (Lawrence et al., 2010). Errors are thus reduced when comparing results for different pH and [Na+] conditions obtained at same temperature on the same fiber, because then CNHE and CNHE/f are the same, as was the case for results shown in Figs. 7 and 9 (B and C).
The NHE system in skeletal muscle is very sensitive to intracellular pH, in part because of the proton-modifier component. Assuming that in the resting mammalian muscle, extracellular [Na+] and pH are constant at 150 mM and 7.40, respectively, and that the intracellular [Na+] is 10 mM, the NHE activity effectively doubles when the cytosolic pH decreases by only 0.2 units from pH 7.20 to 7.00. This high sensitivity ensures that the cytosolic pH is normally well buffered by NHE in a narrow range of pH 7.0–7.2.
For example, using mean values for CNHE (339 pmol/m2) and PH (1.58 × 10−4 m/s) for both the t-system and the sarcolemma, the predicted steady-state cytosolic pH value in resting muscle fibers having a membrane potential Vm = −75 mV under these conditions is 7.233 at 23°C. In this context, note the close match between predicted values based on our measurements and mean values for intracellular pH (7.197) and membrane potential (−76.9 mV) measured in rat EDL muscle fibers at 30°C by Grossie et al. (1988).
The mean predicted NHE rate of proton removal across the t-system membrane of rat fibers at pHcyto 6.8 and 37°C (Eq. 12) is 161 nmol/m2/s. Assuming that this rate applies to the whole rat fiber surface (1,300 cm2/g; Clausen and Hansen, 1974), this translates to ∼1.26 mmol protons/kg/min. Because the proton efflux in muscle during exercise in rats in vivo is ∼6 times greater (7.6 mmol/min/kg; Kemp et al., 1992), it would be interesting to find out in future studies whether the t-system NHE transport activity is up-regulated by exercise by altering the phosphorylation state of the exchanger (Putney et al., 2002) and/or by translocation of new exchanger molecules (Lawrence et al., 2010) to the t-system membrane.
Conclusions
In conclusion, this study shows that the t-system of fast-twitch mammalian fibers has (a) a relatively large proton permeability coefficient that contributes to the relatively fast change in intracellular pH in the fibers and (b) an NHE system whose activity differs markedly between individual fibers and that plays a major role in the regulation of pH under resting conditions.
Acknowledgments
This work was supported by an Australian Research Council (ARC) Discovery Project (DP110102849) to B.S. Launikonis and D.G. Stephenson. B.S. Launikonis was a Future Fellow of the ARC (FT140101309).
The authors declare no competing financial interests.
Eduardo Ríos served as editor.
References
- Aickin C.C., and Thomas R.C.. 1977. Micro-electrode measurement of the intracellular pH and buffering power of mouse soleus muscle fibres. J. Physiol. 267:791–810. 10.1113/jphysiol.1977.sp011838 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aronson P.S. 1985. Kinetic properties of the plasma membrane Na+-H+ exchanger. Annu. Rev. Physiol. 47:545–560. 10.1146/annurev.ph.47.030185.002553 [DOI] [PubMed] [Google Scholar]
- Carter N.W., Rector F.C. Jr., Campion D.S., and Seldin D.W.. 1967. Measurement of intracellular pH of skeletal muscle with pH-sensitive glass microelectrodes. J. Clin. Invest. 46:920–933. 10.1172/JCI105598 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cha C.Y., Oka C., Earm Y.E., Wakabayashi S., and Noma A.. 2009. A model of Na+/H+ exchanger and its central role in regulation of pH and Na+ in cardiac myocytes. Biophys. J. 97:2674–2683. 10.1016/j.bpj.2009.08.053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clausen T., and Hansen O.. 1974. Oubain binding and Na+-K+ transport in rat muscle cells and adipocytes. Biochim. Biophys. Acta. 345:387–404. 10.1016/0005-2736(74)90200-4 [DOI] [Google Scholar]
- Desir G.V., Cragoe E.J. Jr., and Aronson P.S.. 1991. High affinity binding of amiloride analogs at an internal site in renal microvillus membrane vesicles. J. Biol. Chem. 266:2267–2271. [PubMed] [Google Scholar]
- Dulhunty A.F. 1984. Heterogeneity of T-tubule geometry in vertebrate skeletal muscle fibres. J. Muscle Res. Cell Motil. 5:333–347. 10.1007/BF00713111 [DOI] [PubMed] [Google Scholar]
- Edwards J.N., Cully T.R., Shannon T.R., Stephenson D.G., and Launikonis B.S.. 2012. Longitudinal and transversal propagation of excitation along the tubular system of rat fast-twitch muscle fibres studied by high speed confocal microscopy. J. Physiol. 590:475–492. 10.1113/jphysiol.2011.221796 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garciarena C.D., Ma Y.L., Swietach P., Huc L., and Vaughan-Jones R.D.. 2013. Sarcolemmal localisation of Na+/H+ exchange and Na+-HCO3- co-transport influences the spatial regulation of intracellular pH in rat ventricular myocytes. J. Physiol. 591:2287–2306. 10.1113/jphysiol.2012.249664 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gensure R.H., Zeidel M.L., and Hill W.G.. 2006. Lipid raft components cholesterol and sphingomyelin increase H+/OH- permeability of phosphatidylcholine membranes. Biochem. J. 398:485–495. 10.1042/BJ20051620 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Good N.E., Winget G.D., Winter W., Connolly T.N., Izawa S., and Singh R.M.. 1966. Hydrogen ion buffers for biological research. Biochemistry. 5:467–477. 10.1021/bi00866a011 [DOI] [PubMed] [Google Scholar]
- Grinstein S., and Smith J.D.. 1987. Asymmetry of the Na+/H+ antiport of dog red cell ghosts. Sidedness of inhibition by amiloride. J. Biol. Chem. 262:9088–9092. [PubMed] [Google Scholar]
- Grossie J., Collins C., and Julian M.. 1988. Bicarbonate and fast-twitch muscle: Evidence for a major role in pH regulation. J. Membr. Biol. 105:265–272. 10.1007/BF01871003 [DOI] [PubMed] [Google Scholar]
- Hoffmann E.K., and Simonsen L.O.. 1989. Membrane mechanisms in volume and pH regulation in vertebrate cells. Physiol. Rev. 69:315–382. [DOI] [PubMed] [Google Scholar]
- Izutsu K.T. 1972. Intracellular pH, H ion flux and H ion permeability coefficient in bullfrog toe muscle. J. Physiol. 221:15–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Juel C. 2000. Expression of the Na+/H+ exchanger isoform NHE1 in rat skeletal muscle and effect of training. Acta Physiol. Scand. 170:59–63. 10.1046/j.1365-201x.2000.00759.x [DOI] [PubMed] [Google Scholar]
- Juel C. 2008. Regulation of pH in human skeletal muscle: Adaptations to physical activity. Acta Physiol. (Oxf.). 193:17–24. 10.1111/j.1748-1716.2008.01840.x [DOI] [PubMed] [Google Scholar]
- Kemp G.J., Thompson C.H., and Radda G.K.. 1992. Proton efflux from rat skeletal muscle in vivo: Changes in hypertension. Clin. Sci. 82:489–491. 10.1042/cs0820489 [DOI] [PubMed] [Google Scholar]
- Knuth S.T., Dave H., Peters J.R., and Fitts R.H.. 2006. Low cell pH depresses peak power in rat skeletal muscle fibres at both 30 degrees C and 15 degrees C: Implications for muscle fatigue. J. Physiol. 575:887–899. 10.1113/jphysiol.2006.106732 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamb G.D., and Stephenson D.G.. 1990. Calcium release in skinned muscle fibres of the toad by transverse tubule depolarization or by direct stimulation. J. Physiol. 423:495–517. 10.1113/jphysiol.1990.sp018036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamb G.D., and Stephenson D.G.. 1994. Effects of intracellular pH and [Mg2+] on excitation-contraction coupling in skeletal muscle fibres of the rat. J. Physiol. 478:331–339. 10.1113/jphysiol.1994.sp020253 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamb G.D., Recupero E., and Stephenson D.G.. 1992. Effect of myoplasmic pH on excitation-contraction coupling in skeletal muscle fibres of the toad. J. Physiol. 448:211–224. 10.1113/jphysiol.1992.sp019037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Launikonis B.S., and Stephenson D.G.. 1999. Effects of β-escin and saponin on the transverse-tubular system and sarcoplasmic reticulum membranes of rat and toad skeletal muscle. Pflugers Arch. 437:955–965. 10.1007/s004240050867 [DOI] [PubMed] [Google Scholar]
- Launikonis B.S., and Stephenson D.G.. 2001. Effects of membrane cholesterol manipulation on excitation-contraction coupling in skeletal muscle of the toad. J. Physiol. 534:71–85. 10.1111/j.1469-7793.2001.00071.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Launikonis B.S., and Stephenson D.G.. 2002a Tubular system volume changes in twitch fibres from toad and rat skeletal muscle assessed by confocal microscopy. J. Physiol. 538:607–618. 10.1113/jphysiol.2001.012920 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Launikonis B.S., and Stephenson D.G.. 2002b Properties of the vertebrate skeletal muscle tubular system as a sealed compartment. Cell Biol. Int. 26:921–929. 10.1006/cbir.2002.0942 [DOI] [PubMed] [Google Scholar]
- Launikonis B.S., and Stephenson D.G.. 2004. Osmotic properties of the sealed tubular system of toad and rat skeletal muscle. J. Gen. Physiol. 123:231–247. 10.1085/jgp.200308946 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Launikonis B.S., Barnes M., and Stephenson D.G.. 2003. Identification of the coupling between skeletal muscle store-operated Ca2+ entry and the inositol trisphosphate receptor. Proc. Natl. Acad. Sci. USA. 100:2941–2944. 10.1073/pnas.0536227100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawrence S.P., Holman G.D., and Koumanov F.. 2010. Translocation of the Na+/H+ exchanger 1 (NHE1) in cardiomyocyte responses to insulin and energy-status signalling. Biochem. J. 432:515–523. 10.1042/BJ20100717 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madshus I.H. 1988. Regulation of intracellular pH in eukaryotic cells. Biochem. J. 250:1–8. 10.1042/bj2500001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitra K., Ubarretxena-Belandia I., Taguchi T., Warren G., and Engelman D.M.. 2004. Modulation of the bilayer thickness of exocytic pathway membranes by membrane proteins rather than cholesterol. Proc. Natl. Acad. Sci. USA. 101:4083–4088. 10.1073/pnas.0307332101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mollenhauer H.H., Morré D.J., and Rowe L.D.. 1990. Alteration of intracellular traffic by monensin; mechanism, specificity and relationship to toxicity. Biochim. Biophys. Acta. 1031:225–246. 10.1016/0304-4157(90)90008-Z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen O.B., Ørtenblad N., Lamb G.D., and Stephenson D.G.. 2004. Excitability of the T-tubular system in rat skeletal muscle: Roles of K+ and Na+ gradients and Na+-K+ pump activity. J. Physiol. 557:133–146. 10.1113/jphysiol.2003.059014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ørtenblad N., and Stephenson D.G.. 2003. A novel signalling pathway originating in mitochondria modulates rat skeletal muscle membrane excitability. J. Physiol. 548:139–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paula S., Volkov A.G., Van Hoek A.N., Haines T.H., and Deamer D.W.. 1996. Permeation of protons, potassium ions, and small polar molecules through phospholipid bilayers as a function of membrane thickness. Biophys. J. 70:339–348. 10.1016/S0006-3495(96)79575-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedersen T.H., Nielsen O.B., Lamb G.D., and Stephenson D.G.. 2004. Intracellular acidosis enhances the excitability of working muscle. Science. 305:1144–1147. 10.1126/science.1101141 [DOI] [PubMed] [Google Scholar]
- Posterino G.S., Lamb G.D., and Stephenson D.G.. 2000. Twitch and tetanic force responses and longitudinal propagation of action potentials in skinned skeletal muscle fibres of the rat. J. Physiol. 527:131–137. 10.1111/j.1469-7793.2000.t01-2-00131.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Putney L.K., Denker S.P., and Barber D.L.. 2002. The changing face of the Na+/H+ exchanger, NHE1: Structure, regulation, and cellular actions. Annu. Rev. Pharmacol. Toxicol. 42:527–552. 10.1146/annurev.pharmtox.42.092001.143801 [DOI] [PubMed] [Google Scholar]
- Stephenson D.G. 2006. Tubular system excitability: An essential component of excitation-contraction coupling in fast-twitch fibres of vertebrate skeletal muscle. J. Muscle Res. Cell Motil. 27:259–274. 10.1007/s10974-006-9073-6 [DOI] [PubMed] [Google Scholar]
- Stephenson D.G., and Lamb G.D.. 1993. Visualization of the transverse tubular system in isolated intact and in mechanically skinned muscle fibres of the cane toad by confocal laser scanning microscopy. J. Physiol. 459:15P. [Google Scholar]
- Tiruppathi C., Miyamoto Y., Ganapathy V., and Leibach F.H.. 1988. Fatty acid-induced alterations in transport systems of the small intestinal brush-border membrane. Biochem. Pharmacol. 37:1399–1405. 10.1016/0006-2952(88)90800-3 [DOI] [PubMed] [Google Scholar]
- Vaughan-Jones R.D., and Wu M.-L.. 1990. Extracellular H+ inactivation of Na+-H+ exchange in the sheep cardiac Purkinje fibre. J. Physiol. 428:441–466. 10.1113/jphysiol.1990.sp018221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willoughby D., Thomas R.C., and Schwiening C.J.. 1998. Comparison of simultaneous pH measurements made with 8-hydroxypyrene-1,3,6-trisulphonic acid (HPTS) and pH-sensitive microelectrodes in snail neurones. Pflugers Arch. 436:615–622. 10.1007/s004240050679 [DOI] [PubMed] [Google Scholar]