Genomic Signature of Adaptive Divergence despite Strong Nonadaptive Forces on Edaphic Islands: A Case Study of Primulina juliae

Abstract

Both genetic drift and divergent selection are expected to be strong evolutionary forces driving population differentiation on edaphic habitat islands. However, the relative contribution of genetic drift and divergent selection to population divergence has rarely been tested simultaneously. In this study, restriction-site associated DNA-based population genomic analyses were applied to assess the relative importance of drift and divergent selection on population divergence of Primulina juliae, an edaphic specialist from southern China. All populations were found with low standing genetic variation, small effective population size (N_E), and signatures of bottlenecks. Populations with the lowest genetic variation were most genetically differentiated from other populations and the extent of genetic drift increased with geographic distance from other populations. Together with evidence of isolation by distance, these results support neutral drift as a critical evolutionary driver. Nonetheless, redundancy analysis revealed that genomic variation is significantly associated with both edaphic habitats and climatic factors independently of spatial effects. Moreover, more genomic variation was explained by environmental factors than by geographic variables, suggesting that local adaptation might have played an important role in driving population divergence. Finally, outlier tests and environment association analyses identified 31 single-nucleotide polymorphisms as candidates for adaptive divergence. Among these candidates, 26 single-nucleotide polymorphisms occur in/near genes that potentially play a role in adaptation to edaphic specialization. This study has important implications that improve our understanding of the joint roles of genetic drift and adaptation in generating population divergence and diversity of edaphic specialists.

Introduction

Edaphic factors are key aspects that contribute to biodiversity and patterns of endemism. Unique soils, such as serpentine, limestone, gypsum, and dolomite, are widely cited study systems for conservation, ecology, and evolution (Palacio et al. 2007). Due to highly heterogeneous landscapes, special edaphic habitats generally support a large number of endemic species, which make an outsized contribution to regional species diversity and endemism. For example, in the Southwest Australian Floristic Region, granite outcrops account for less than 1% of the region, but harbor 17% of its native vascular plants (Hopper et al. 1997; Hopper and Gioia 2004). Similarly, the serpentine habitats of the California Floristic Province cover only 1.5% of the region, but support 12.5% of the region’s endemic plant species (Safford et al. 2005). However, edaphic specialists and other plant species restricted to special soils are particularly sensitive to habitat loss and climate change, because of their small population sizes and habitat specialization (Damschen et al. 2010, 2012; Ghasemi et al. 2015).

Landscapes associated with special soils are typically characterized by naturally fragmented and isolated habitats and may act as “edaphic islands” in evolutionary processes for plants. In these island landscapes, genetic drift and/or divergent selection may act on standing genetic variation and new mutations, contributing to population divergence and speciation (Wright 1931, 1951). To date, most studies on edaphic islands have mainly focused on those cases where the local adaptation has generated striking patterns of plant evolution (Turner et al. 2010; Arnold et al. 2016; Hendrick et al. 2016). However, such differences among edaphic islands may also be due to genetic drift alone or in concert with natural selection. Thus, investigating the joint roles of local adaptation and genetic drift in driving population differentiation is critical for understanding how edaphic island taxa diverge, thereby contributing to patterns of endemism and plant biodiversity.

Genetic drift is predicted to be strong in edaphic islands because of a suite of evolutionary processes usually detected in spatially isolated populations, including founder effects (Franks 2010), small effective population size (N_E) (Frankham 1998; Eldridge et al. 1999), bottlenecks (Frankham 1998), and limited gene flow (Franks 2010). Divergent selection is also likely to be significant among edaphic islands when there is environmental heterogeneity among different islands (Weigelt et al. 2013). Soil type is the most obvious environment variation among edaphic islands. Most minerals found in plants come exclusively from soil; plants therefore must adapt to soils in order to survive and reproduce (Baxter and Dilkes 2012). Edaphic endemic species may show local adaptation to soil type through natural selection, as evidenced in many serpentine endemics (Sambatti and Rice 2006; Turner et al. 2010; Moyle et al. 2012; Arnold 2016). Other potential sources of environmental variation among edaphic islands are components of climate, including temperature and precipitation, which may directly influence microhabitat availability for plant species. Therefore, either or both genetic drift and divergent selection could drive population genetic differentiation among edaphic islands. However, drift may overwhelm selection if it is much stronger, such as when effective population sizes are very small, thereby precluding local adaptation (Wright 1931, 1951).

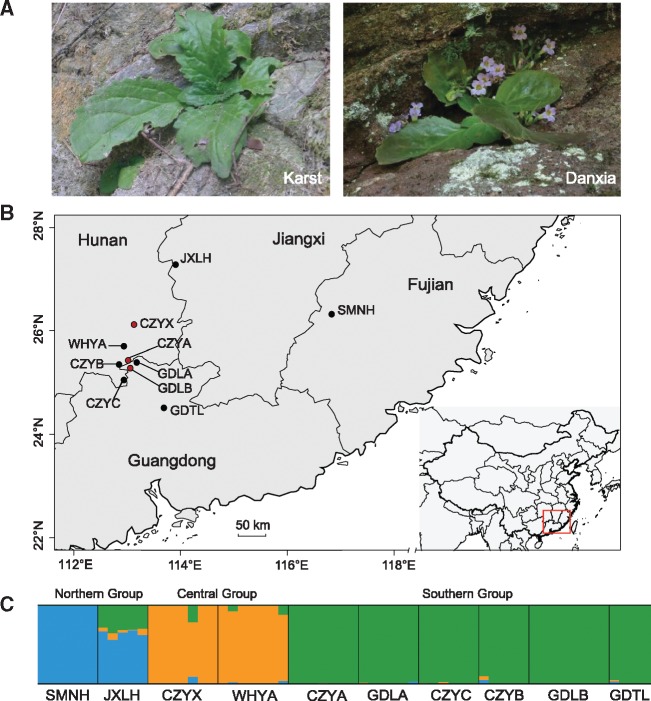
Both Karst and Danxia landforms are edaphically special terrestrial habitat islands found in southern China. Soils derived from limestone Karst (i.e., carbonate bedrock) are usually shallow (fig. 1A) and characterized by high concentrations of calcium (Ca) and magnesium (Mg), as well as high pH (Hao et al. 2015). Danxia soils (after Danxia Mountain in Guangdong Province, China), usually red or purple in color, are derived from red terrigenous sediments (sandstones and conglomerates; fig. 1A) and are similar to Karst soil with the exception of containing lower concentrations of C, N, and P (Hao et al. 2015). Karst and Danxia landforms in southern China, especially those surrounding the Nanling Mountains, are typically dominated by steep-sided towers, caves, sinkholes, and cliffs, that exhibit disjunct distributions in the form of soil-island outcrops (i.e., edaphic islands), with special soils being surrounded by normal soil types or vice versa (Hao et al. 2015). Additionally, both Karst and Danxia soils are highly porous with low water storage capacities and thus prone to chronic drought. Such extreme habitats may exert strong selective forces on plant evolution, contributing to the remarkably high endemism and species richness of South China.

Fig. 1.

—Habitat pictures for Primulina juliae in Karst and Danxia (A), sampling sites (inset map shows the sampling location on China map) for ten populations of P. juliae analyzed in the present study (B), and the results for structure analysis (C). Red and black dots indicate Danxia and Karst habitat, respectively.

Due to their unique natural landforms and the associated special biota, “South China Karst” and “China Danxia” were both listed as World Natural Heritage sites by UNESCO, with significant need for protection. These areas were also recognized as global centers of plant diversity by IUCN (Davis et al. 1995), and represent excellent regions for plant evolution studies due to the highly heterogeneous topography with patches of habitat of varying isolation, landforms, and soil types. However, the actual evolutionary mechanisms driving plant diversification on edaphic islands in Karst and Danxia landscapes are not well known. One important, yet unanswered question is whether population divergence is mainly driven by genetic drift or divergent selection (i.e., local adaptation). In addition, understanding the mechanisms of evolution and diversification in Karst and Danxia landscapes is particularly important for plant conservation as both landscapes are disproportionately threatened by climate change and anthropogenic deforestation (Sodhi et al. 2004; Clements et al. 2006).

Primulina juliae is a perennial herb mainly distributed around Nanling Mountains, with few populations extending to Jiangxi and Fujian provinces in eastern China. Primulina is the most speciose genus within the Old World Gesneriacese family, with about 180 described species in China (Xu et al. 2017). Hao et al. (2015) analyzed soil properties for 100 species of Primulina and revealed a high degree of edaphic heterogeneity among species in this genus. Unlike most Primulina species that only grow on a single type of soil (either Karst, Danxia, or normal soil; Hao et al. 2015), P. juliae occurs on both special soils (i.e., Karst and Danxia), with most populations restricted to Karst landscapes. Due to its high edaphic specialization and limited dispersal ability, P. juliae generally occurs in highly fragmented and isolated patches with clearly defined geographical boundaries. These features make P. juliae an excellent model system for studying evolution of edaphic endemics. If population divergence is mainly driven by physical distance (geography), we expect a pattern of isolation by distance (IBD, Wright 1943; Rousset 1997) among populations, which has been detected in congeneric species (Gao et al. 2015). In this scenario, there would be little correlation between soil types or environmental factors, and genetic structure, making nonadaptive processes more important than local adaptation in driving population differentiation. Alternatively, if substantial genetic variation is explained by soil habitats or other environment factors, this would suggest a history of local adaptation, that is, isolation by environment (IBE). In this scenario, genomic scans and association tests could detect outlier loci due to divergent selection.

Here, we utilized a population genomic approach, employing single-nucleotide polymorphisms (SNPs) obtained from restriction-site associated DNA (RAD) sequencing (Baird et al. 2008) to explore the relative roles of genetic drift and divergent selection in causing genomic divergence among edaphic island populations of P. juliae. Information from genome-wide markers greatly improves statistical power and precision compared to traditional population genetics approaches with small numbers of markers. This enhances our ability to address the relative role of these forces by increasing power to test for bottlenecks, to estimate effective population size (N_E) in small populations, and to identify outliers or loci associated with selective forces. The specific goals of this study were to: 1) characterize the genetic population structure of P. juliae; 2) test the prediction that genetic drift contributes to differentiation among edaphic island populations; 3) test the hypothesis that divergent selection caused by local environments contributes to genetic differentiation among populations; and 4) identify potentially adaptive loci under divergent selection. Finally, we discuss the conservation implications of our findings.

Materials and Methods

Population Sampling, DNA Extraction, and RAD Sequencing

A total of 67 individuals from 10 populations (5–8 per population) were sampled across the geographic range of P. juliae, including three Danxia populations and seven Karst populations (table 1 and fig. 1B). Eight samples of Primulina eburnea from a population in Chenzhou (Hunan Province) were collected as an outgroup (data not shown). The genome size of P. juliae is about 2 C = 2.51 pg (Kang et al. 2014). Total genomic DNA was extracted from the fresh leaves using a modified cetyltrimethylammonium bromide (CTAB) method (Doyle and Doyle 1987). RAD library construction and sequencing were performed by Novogene Bioinformatics Institute (Beijing, China). Genomic DNA was first normalized to a concentration of 50 ng/μl, digested with restriction endonuclease EcoRI and then processed into multiplexed RAD libraries following established methods (Baird et al. 2008). Sequencing adaptors and individual barcodes were ligated to EcoRI-digested fragments and amplified by polymerase chain reaction (PCR). The RAD libraries were run on an Illumina HiSeq 2000 platform (San Diego, CA) with paired-end 100-bp reads.

Table 1.

Sampling Information, Summary Statistics of Polymorphism, Effective Population Size Estimates, and the Results of Bottleneck Test for Ten Populations of Primulina juliae Based on 5,176 SNP Loci

Population	Latitude (°N)	Longitude (°E)	Habitat	N	PPL	A	Ae	HO	HE	FIS	NE (95% CI)	Wilcoxon’s Sign-Rank Test	Mode-Shift Test
SMNH	26.32	116.83	Karst	8	6.0	0.9	0.8	0.020	0.022	0.065	2.3 (2.1–2.5)	0.000	Shifted mode
JXLH	27.28	113.91	Karst	5	6.5	0.9	0.8	0.021	0.021	−0.043	3.9 (3.1–4.9)	0.000	Shifted mode
CZYX	26.12	113.13	Danxia	7	14.5	1.0	0.9	0.047	0.052	0.064	2.1 (2.0–2.2)	0.000	Shifted mode
WHYA	25.70	112.94	Karst	7	12.7	1.0	0.9	0.070	0.047	−0.307	1.3 (1.2–1.3)	0.000	Shifted mode
CZYA	25.43	113.02	Danxia	7	22.3	1.1	1.0	0.069	0.071	0.012	4.6 (3.9–5.4)	0.000	Shifted mode
GDLA	25.39	113.18	Karst	6	16.2	1.0	1.0	0.050	0.057	0.083	5.0 (4.0–6.1)	0.000	Shifted mode
CZYB	25.35	112.85	Karst	5	16.0	1.0	0.9	0.052	0.056	0.041	6.3 (4.8–8.0)	0.000	Shifted mode
GDLB	25.28	113.06	Danxia	8	23.5	1.1	1.0	0.064	0.071	0.074	5.9 (4.9–6.8)	0.000	Shifted mode
CZYC	25.05	112.94	Karst	6	18.4	1.1	1.0	0.056	0.063	0.074	6.3 (5.1–7.6)	0.000	Shifted mode
GDTL	24.51	113.69	Karst	6	4.5	1.0	0.9	0.012	0.013	0.078	2.9 (2.4–3.4)	0.000	Shifted mode

Note.— N, the number of individuals analyzed; PPL (%), percentage of polymorphic SNP loci; A, number of alleles; A_e, effective number of alleles; H_O, observed heterozygosity; H_E, expected heterozygosity; F_IS, fixation index; N_E (95% CI), effective population size estimates with 95% confidence intervals.

Bioinformatics Treatments

We used only the forward reads of the paired ends (with the restriction site) in subsequent analyses due to low coverage of the reverse reads. We followed established practices for data analysis using Stacks 1.43 software pipeline (Catchen et al. 2013). Reads were filtered for quality by identifying and removing PCR duplicates, and looking for the presence of a correct barcode and the EcoRI recognition site using stacks. Files containing all clean RAD tags for all individuals were analyzed in stacks, using de novo assembly. As a first step, all sequences were processed in ustacks, which aligns a set of short-read sequences from a single individual into exactly matching stacks. These stack for a set of loci; SNPs are detected at each locus by comparing the stacks using a maximum-likelihood framework (Hohenlohe et al. 2010). We set the minimum depth of coverage to create a stack at five sequences and the maximum distance allowed between stacks as two nucleotides. We enabled the Deleveraging algorithm to resolve over-merged tags, the Removal algorithm to drop highly repetitive stacks, and nearby error detection. We used an alpha value of 0.05 for the SNP model. We used Cstacks to build a catalog of consensus loci containing all the stacks (loci) from all the individuals and merged all alleles together. Next we compared each individual genotype against the merged catalog using sstacks. Finally, we used the Populations program to obtain the loci that were present in at least 80% of the individuals from each population in at least eight populations with at least five RAD tags per allele at each locus (5X coverage per allele). We only included the first SNP per locus in the final analysis to avoid linkage bias for the SNP calling. We removed loci with minor allele frequencies <0.05, as low frequency alleles may represent PCR errors. Additionally, a maximum observed heterozygosity was set at 0.5 to process a nucleotide site at a locus. We further removed loci with extremely high coverage (coverage greater than 2SD above the mean) or exhibiting three alleles within individuals to avoid possible paralogs (Emerson et al. 2010) using vcftools (Danecek et al. 2011). Finally, individuals with extremely low genotype coverage rate (< 60%) were removed. We generated input files for downstream analyses using pgdspider (Lischer and Excoffier 2012).

Summary Statistics and Analysis of Population Genetic Structure

Summary statistics, including percentage of polymorphic loci (PPL), the number of different alleles (A), the number of effective alleles (A_e), observed heterozygosity (H_O), expected heterozygosity (H_E), and fixation index (F_IS) for each population was estimated using GenAlEx v6.502 (Peakall and Smouse 2012). To partition genetic variance, we used analysis of molecular variance (AMOVA) with arlequin 3.5 (Excoffier and Lischer 2010) at three levels: among groups (soil types, F_CT), among populations within group (F_SC), and among individuals within populations. We also estimated F_ST among all populations, between habitat types, and between each pair of populations. The significance of variance components was estimated with 1,000 permutations. We used a Bayesian clustering approach implemented in structure v2.3.4. (Pritchard et al. 2000) to infer the number of clusters and to assign individuals to these clusters. We ran 10 independent replicates for each K value between 1 and 10, with 500, 000, and 1, 000, 000 steps being the length of burn-in and Markov chain Monte Carlo, respectively. The admixture model and correlated allele frequencies between populations were specified for each run. We used structureharvester (Earl and Vonholdt 2012) to summarize population structure and the identification of optimal K through the method of Evanno et al. (2005). We combined results across replicate runs using the program clumpp (Jakobsson and Rosenberg 2007) and visualized the output with distruct v1.1 (Rosenberg 2004). Additionally, we explored population structure with a principal component analysis (PCA) using the SNPRelate package (Zheng et al. 2012) in R (R Core Development Team 2010). We also characterized population structure with discriminant analysis of principal component (DAPC), a method requiring no assumptions about an evolutionary model, using adegenet package (Jombart 2008) in R.

Detecting Signatures of Demographic History

Under a scenario of strong genetic drift in small isolated populations, we expect to detect loss of genetic variation, small effective population sizes (N_E), and/or signature of bottlenecks. We estimated N_E and tested for bottlenecks for each population. Effective population size (N_E) of P. juliae populations was estimated using the molecular coancestry method implemented in program neestimator 2.01 (Do et al. 2014). We tested for signatures of population bottlenecks using the program bottleneck 1.2.02 (Cornuet and Luikart 1996; Piry et al. 1999). This algorithm uses the loss of rare alleles predicted in recently bottlenecked populations. We used the infinite alleles model (IAM) as the most appropriate evolutionary model for SNP loci. A one-tailed Wilcoxon signed rank test was performed in order to test for significant heterozygosity excess compared to the level predicted under mutation-drift equilibrium. We further examined the contribution of genetic drift to differentiation among populations using the maximum likelihood (ML) approach implemented in treemix program (Pickrell and Pritchard 2012). treemix estimates a population-level phylogeny on the basis of the allele frequencies as well as a Gaussian approximation to genetic drift. The population of P. eburnea was used as outgroup for all the trees. We assumed independence of all SNPs in generating the ML tree.

Genetic, Geographic, Habitat, and Environmental Correlations

Geographic distance often contributes to patterns of distribution and genetic differentiation in the form of IBD, where the degree of genetic differentiation between two populations is correlated with their geographic distance. To assess the relationship between geographic distance and genetic distance, we conducted IBD analyses using arlequin across all populations. We calculated pairwise geographic distances using the Geographic Distance Matrix Generator version 1.2.3 (http://biodiversityinformat- ics.amnh.org/open_source/gdmg) where the genetic distance matrix consisted of pairwise F_ST values derived from arlequin. Alternatively, if adaptive divergence causes sufficient genetic isolation along a pathway toward ecological speciation, IBE occurs, whereby genome-wide genetic differentiation is correlated with environmental differences among populations (Nosil et al. 2008). The large contribution of environmental differences to population differentiation has long been recognized and described as IBE (Lexer et al. 2014; Wang and Bradburd 2014; Manthey and Moyle 2015; Pluess et al. 2016). Several studies have highlighted the importance of incorporating environmental distances when exploring patterns of genetic differentiation. In the present study, 20 environmental predictors including soil types and climatic factors were considered (supplementary table S1, Supplementary Material online). IBE was tested separately with habitat (IBE-habitat) and climatic variable (IBE-clim) distances among populations, respectively. For pairwise habitat distance, we assume 1 for a pair of populations from different soil types and 0 otherwise. Climatic data for all populations were taken from the WorldClim database (Hijmans et al. 2005). The 19 climatic variables (supplementary table S1, Supplementary Material online) were first subject to PCA using JMP 13.0.0 (SAS, Cary, NC). The first two principal components (Clim_PC1 and Clim_PC2) were then used as points in two dimensions to calculate a pairwise distance matrix for all populations. Both IBE-habitat and IBE-clim were assessed with IBDWS (Jensen et al. 2005).

In order to simultaneously estimate the effects of geography and environment on genomic variation, we partitioned the proportion of genome-wide SNP variation among populations that could be explained by geography, habitat, climatic factors, and their collinear portion using redundancy analyses (van den Wollenberg 1977; Peres-Neto et al. 2006), an eigen analysis ordination method implemented in the vegan package in R (Oksanen et al. 2015). This analysis is able to provide a statistical means for inferring the effect of partially confounded variables separately and assess the explanatory power of multivariate predictors (habitat, geographic, and climatic variables) for multivariate responses (SNPs). We used an initial model of: Y (individual genotype) ∼ Habitat + Clim_PC1 + Clim_PC2 +Latitude + Longitude. First, we used permutation tests to assess the global significance of the RDA by performing 1,000 permutations where the genotypic data were permuted randomly and the model was refitted, thereby assessing whether the different variables significantly influenced allele frequencies. Second, we tested the significance of each individual variable by running an RDA marginal effects permutation test (with 1,000 permutations) where we removed each term one by one from the model containing all other terms. We only retained significant effects in the final model. To determine the role of each individual variable independently from other possible sources of genetic variation (i.e., the remaining explanatory variables in the final model), we performed a conditioned (partial) RDA where the effects of all but the tested significant explanatory variables were removed from the ordination by using the condition function. Finally, the distribution of SNP contributions to the single considered variable RDA axis after conditioning on remaining variables was compared with that obtained for conditioned RDA estimating the specific effect of other variables. We expect that directional selection on loci conferring adaptation to habitat or climatic factors will generate outlier SNPs in the distribution of SNP contributions to the effect of habitat or climatic factors (Lasky et al. 2015; Szulkin et al. 2016). Therefore, we predict that the distribution of SNP contributions to the conditioned effect of habitat or climatic variables will differ from the conditioned effect of geography if the IBE pattern is primarily driven by directional selection.

Genome-Wide Signatures of Diversifying Selection

We used two well-established approaches to scan for genome-wide signatures of diversifying selection. First, F_ST outliers were identified using allele frequencies with BayeScan v2.1 (Foll and Gaggiotti 2008) among all populations. The approach implemented in BayeScan directly estimates the probability that each locus is subject to selection by decomposing locus-population F_ST coefficients into a population-specific component (beta) shared by all loci and a locus-specific component (alpha) shared by all the populations (Foll and Gaggiotti 2008). For any given locus, a negative value suggests balancing selection is homogenizing allele frequencies over populations, while positive value of alpha indicates that the locus is under adaptive selection (Foll and Gaggiotti 2008). We ran 20 pilot runs of 5,000 iterations and an additional burn-in of 50,000 iterations, followed by 50,000 iterations with a sample size of 5,000 and a thinning interval of 10 to identify loci under selection from locus-specific Bayes factors. In this analysis, Log10 values of the posterior odds (PO) > 0.5 and 2.0 are considered as being a “substantial” and “decisive” evidence for selection, respectively (Jefferys 1961). We set the false discovery rate (FDR) to 0.05.

Second, BayPass 2.1 (Gautier 2015) was used to scan for a signature of adaptive divergence among all populations based on a calibration procedure of the XtX differentiation measure (Günther and Coop 2013). This statistic can be interpreted as a SNP-specific F_ST explicitly corrected for the scaled covariance of population allele frequencies. The pseudo-observed data sets (PODs) analysis provides estimates of a decision criterion (i.e., a 1% threshold XtX value) for selection (Gautier 2015). Similar analyses were performed to detect signature of adaptive selection between habitats with all the methods described above.

To complement our F_ST outlier tests, we tested for loci associated with habitat or environmental variation using BayPass under the core model, as the aux and std models may be unstable for highly differentiated populations (Günther et al., personal communication), which is the scenario for our data based on the genetic differentiation results. As described above, we considered habitat, Clim_PC1, and Clim_PC2 as covariables for each population. Five independent analyses were run in order to check consistency of the resulting estimates across runs. Finally, calibration of the Bayes Factor (BF) was performed using PODs, with the 1% threshold being used to infer significant association.

Loci Annotation

To explore putative coding regions linked to outlier or associated loci, we identified candidate genes in genomic regions (within 10 kb) surrounding our RAD-Tags, which required an annotated reference genome. As no reference genome is available for P. juliae, we identified candidate genes within the recently annotated genome of the closely related species Primulina huaijiensis (C. Feng, unpublished data), with genome size 2 C = 1.12 pg (Kang et al. 2014). We aligned the full length (100 bp long) consensus sequence of each polymorphic RAD locus to the P. huaijiensis genome using BWA software (Li and Durbin 2009). Genes in or closely linked to outlier loci were functionally categorized according to the Gene Ontology (GO) terminology categories (biological process, molecular function, and cellular component) and the resulting GOs were enriched using the agriGO 1.2 (Du et al. 2010). We used the GO analysis to test for overrepresentation of genes associated with specific biological processes relative to the full set genes of Arabidopsis thaliana.

Results

Characterization of Data Set

Sequencing RAD-Tags from P. juliae populations yielded 327, 553, and 259 clean reads across 67 individuals. The minimum and maximum number of sequence reads per sample was 1, 062, 061 and 14, 073, 399, respectively, with the median value being 4, 888, 855. Applying the criteria of genotyping call rate, MAF, heterozygosity, and depth of coverage thresholds efficiently removed poorly sequenced tags and artefactual SNPs originating from sequencing errors or paralogous tags. The resulting data set is characterized by a minimum of 80% genotype call rate for each population, at least eight populations, a 0.5 heterozygosity and 5% MAF threshold. A total of 5,176 variable SNP loci were available for analysis without P. eburnea, while the inclusion of P. eburnea as outgroup led to a total of 5,542 SNPs, which were only used for analyses with treemix. Specifically, mean coverage per locus across individuals varied between 7 and 29 (median = 14.4; supplementary fig. S1, Supplementary Material online), and the number of loci per individual ranged from 3,340 to 4,671 (median = 4,153, i.e., about 80% of all variable SNPs; supplementary fig. S2, Supplementary Material online) for the data set without P. eburnea.

Analysis of Population Genetic Structure

We detected significant signal of genetic differentiation between Danxia and Karst habitats, with the value of genetic differentiation being 0.126 (P < 0.001). Hierarchical AMOVA showed high differentiation among populations within habitats (F_SC = 0.756, P < 0.001), whereas no significant differentiation was detected between habitats (F_CT = 0.000, P = 0.788). Pairwise F_ST analyses among populations also indicated consistently significant genetic differentiation, with the value ranged from 0.152 (CZYB vs. GDLB) to 0.944 (SMNH vs. GDTL) (table 2).

Table 2.

Pairwise F_ST Values among Ten Populations of Primulina juliae Based on 5,176 SNP Loci

Population	SMNH	JXLH	CZYX	WHYA	CZYA	GDLA	CZYB	GDLB	CZYC
JXLH	0.863
CZYX	0.874	0.807
WHYA	0.888	0.837	0.620
CZYA	0.848	0.759	0.645	0.712
GDLA	0.868	0.795	0.687	0.748	0.401
CZYB	0.868	0.802	0.657	0.720	0.372	0.536
GDLB	0.830	0.732	0.626	0.690	0.361	0.495	0.152
CZYC	0.852	0.770	0.658	0.720	0.450	0.535	0.433	0.332
GDTL	0.944	0.935	0.851	0.879	0.737	0.798	0.787	0.712	0.776

Note.—All P-values < 0.0001.

The best-supported value of K in our structure analysis was K = 3 based on the ΔK method. Three core genetic groups (fig. 1C) were revealed, featuring a northern group (SMNH, JXLH), a central group (CZYX, WHYA), and a southern group (CZYA, CZYB, CZYC, GDLA, GDLB, GDTL). Individuals for each population were generally assigned to a single group, while JXLH showed considerable admixture between two groups. As expected, all populations grouped basically by geographic proximity in the PCA, with exception of JXLH being intermediate (supplementary fig. S3A, Supplementary Material online). Similarly, three groups were further identified by the DAPC procedure, with a clear differentiation of northern, central, and southern groups along the PC1 axis, and the PC2 axis further separated the northern populations SMNH and JXLH from the other two groups (supplementary fig. S3B, Supplementary Material online).

Testing Signal of Genetic Drift

All populations had extremely low within-population genetic variation, especially for the three peripheral populations of SMNH, JXLH, and GDTL (table 1). Genetic diversity within populations was highest in GDLB and lowest in GDTL (table 1). We found this pattern for all five measures of genetic variation estimated (PPL, A, Ae, H_O, H_E). Effective population size (N_E) estimated using neestimator were also generally small, ranging from 1.3 to 6.3 (mean = 4.1) (table 1). Additionally, with bottleneck, we found overwhelming evidence for historical bottlenecks in all of the populations (Wilcoxon signed rank test, P = 0.000; shifted mode) (table 1). Finally, treemix results suggested that genetic drift contributed significantly to the genetic differentiation of P. juliae populations, with a substantial increase (threefold to sixfold) in drift in the three peripheral populations (i.e., SMNH, JXLH, and GDTL), as compared with the other populations (fig. 2).

Fig. 2.

—Relationships among Primulina juliae populations inferred using the maximum likelihood method implemented in treemix. Colors correspond to those in figure 1C. treemix also inferred five migration events (depicted by dotted arrows) among populations.

Genetic, Geographic, Habitat, and Environmental Correlations

The first two principal components (Clim_PC1 and Clim_PC2) summarized 53.4% and 35.0%, respectively, of variation in the 19 climatic variables used in this study. Both IBD (fig. 3A) and IBE-clim (fig. 3B) analyses indicated significant correlation between geographic distances, environment distances, and genetic distances across all P. juliae populations, while no significant correlation was detected between habitat and genetic distances (IBE-habitat, r = −0.311, P = 1.000). Additionally, there was significant correlation between geographic and climatic distances (r = 0.719, P = 2.706E⁻⁰⁸, 1,000 permutations).

Fig. 3.

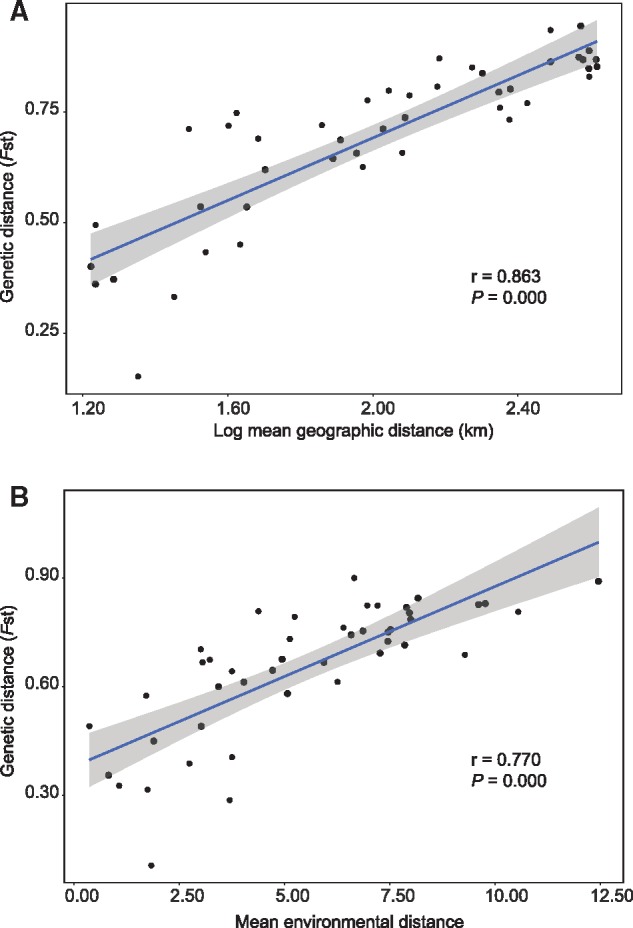
—Geographic, environmental, and genetic correlations. Correlation of mean pairwise geographic distance versus mean pairwise F_ST (A), and correlation of mean pairwise environmental distance versus mean pairwise F_ST (B).

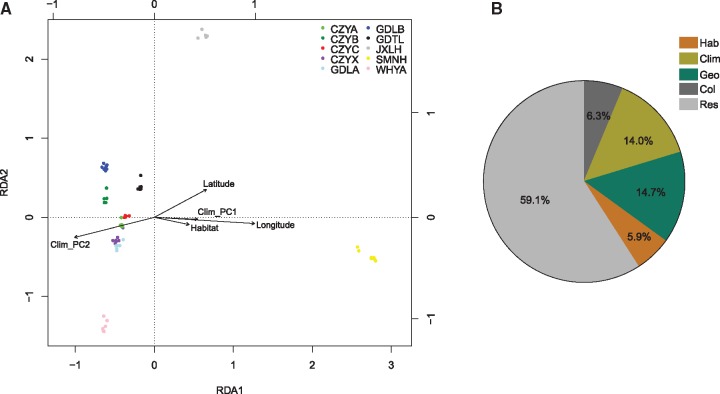
We further performed redundancy analyses to assess the proportion of genome-wide SNP variation that could be explained by geography, habitat, climatic factors, and their collinearity, respectively. The proportion of constrained variance was highly significant (table 3), confirming the informativeness of the constraining variables used in the full RDA model. Five constrained axes explained 40.9% of the total genotypic variance, and the first two RDA axes recovered more than a half (21.0%), owing to a large contribution of both spatial variables and environments (table 4). Both habitat and environment variables were mainly represented by RDA axis 1, and spatial variables were mainly captured by RDA axis 1 and 2 (table 4; fig. 4A). The partial RDA conditioned on other variables revealed a significant effect of habitat, environment, and geography after removing variation caused by the other significant factors (table 3). Therefore, both habitat type and environment factors were significant predictors of genotypic variation independently of geographic distance, but environment variables explained more than twice as much SNP variation (14.0%) than did habitat type (5.9%) (fig. 4B).

Table 3.

Results of RDA Significance Tests (the Proportion of Genotypic Variance Explained, df and P-values Obtained through 1,000 Permutations; Significant P-values are in Bold), Detailed for the Full RDA Analysis (Model with All Significant Terms), and the Marginal Effect of Each Constraining Variable in the Model

	RDA			Conditioned RDA
	% of Variance Explained	df	P-Value	% of Variance Explained	df	P-Value
Global analysis	40.90	5	0.001	—
Residual	59.10	59	—
Marginal test
Habitat	5.90	1	0.001	5.90	1	0.001
Clim_PC1	8.00	1	0.001	7.90	1	0.001
Clim_PC2	6.00	1	0.001	6.00	1	0.001
Longitude	8.40	1	0.001	8.40	1	0.001
Latitude	7.60	1	0.001	7.10	1	0.001
Residual	59.10	59	—	59.10	59	—

Note.—The marginal effect of each constraining variable was tested through permutation tests by removing each term one by one from the model containing all other terms. The conditioned RDA reported conditioned (partial) RDA significance tests for each term, after conditioning on other constraining variables to remove their confounding effects.

Table 4.

Summary of RDA Analyses for Ten Populations of Primulina juliae

RAD Axis	RDA1	RDA2	RDA3	RDA4	RDA5
% of variance explained	12.846	8.159	7.867	6.254	5.771
Constraining variables
Habitat	0.344	−0.072	−0.528	0.698	−0.332
Clim_PC1	0.430	−0.019	0.582	0.687	−0.068
Clim_PC2	−0.788	−0.199	0.575	−0.009	−0.097
Longitude	0.991	−0.061	0.098	0.003	−0.072
Latitude	0.516	0.276	−0.566	−0.580	0.023

Note.—The proportion of genotypic variance explained by each RDA axis is provided, along with the vector coordinates of each constraining variable in the RDA space (see fig. 4). For each RDA axis, the longest vector projection indicates the most important variable explaining variation along that axis.

Fig. 4.

—Multivariate SNP–environment associations. (A) First two canonical axes (RDA1 and RDA2) and RDA of variation in 5,176 SNPs among 65 samples. Each canonical axis represents a linear combination of environmental variables (strongly loading variables shown as arrows) that explains variation in a linear combination of SNPs among samples (colored points represent samples from different populations as shown in the legend). (B) Proportion of total SNP variation among samples explained in RDA by habitat type (Hab, 5.9%), climatic variable (Clim, 14.0%), spatial structure (Geo, 14.7%), or their collinear effect (Col, 6.3%), respectively. Res (59.1%) means residual. The permutation test indicated that both habitat type and environment factors were significant predictors of genotypic variation independently of geographical distance (P = 0.001).

Genome-Wide Footprints of Selection

BayeScan and BayPass analyses found only one consistent high F_ST outlier for habitat-specific divergent selection (supplementary figs. S4 and S5, Supplementary Material online). As to the F_ST outlier test encompassing all the ten populations, BayeScan analyses showed 28 outliers, with all of them being probably under balancing selection (supplementary fig. S6, Supplementary Material online). However, the results from BayPass indicated that 19 diversifying outliers were detected based on XtX calibration (supplementary fig. S7, Supplementary Material online).

The association analysis with BayPass showed much higher consistency across five different runs based on eBPis (r = 0.980, P < 0.0001) than BFis (r = 0.890, P < 0.0001), hence we prefer to use the criterion of eBPis calibration as suggested by Gautier (2015). The results indicated nine, one, and five loci significantly associated with habitat (supplementary fig. S8, Supplementary Material online), Clim-PC1 (supplementary fig. S9A, Supplementary Material online), and Clim-PC2 (supplementary fig. S9B, Supplementary Material online), respectively.

Annotated Loci

We further examined the function of selected or associated loci from BayPass, because of its better statistical performance compared with other software (Gautier 2015). We only considered identity percentages ≥ 95%; stringent searching conditions were used to ensure that the RAD-Tags matches against the P. huaijiensis genome were reliable. Twenty-six out of the 31 loci identified as high XtX outliers or associated loci with habitat or climatic factors blasted to genes, and 16 of these are within the coding region of annotated genes (supplementary table S2, Supplementary Material online), indicating many of these loci are functional. These loci uncovered three categories of genes (i.e., molecular function, cellular component, and biological process). Specifically, some of the diversifying loci were involved in metal ion binding, calcium ion binding, biosynthetic process, metabolic process, structural molecule activity, and DNA damage/repair (supplementary table S2, Supplementary Material online). When compared to the well-annotated A. thaliana genome, they were enriched in two different GO terms (Bonferroni-corrected P < 0.05): GO: 0005515 protein binding found in two genes (AT5G21090 and AT4G33210), and GO: 0000166 nucleotide binding also found in two genes (AT3G57330 and AT2G29940). Both GO terms belong to the category of molecular function.

Discussion

Our analysis employing a large number of genome-wide SNPs revealed low genetic diversity (measured as H_E and percentage of PPL) within populations and strong genetic differentiation among populations in P. juliae. Consistent with this result, high levels of genetic divergence have commonly been reported for plant taxa endemic to terrestrial island-like habitats (e.g., inselbergs) across the world. For example, high population differentiation has been observed for bromeliad species on tropical inselbergs in South America (Barbará et al. 2007; Palma-Silva et al. 2011). Additionally, low genetic diversity and high genetic differentiation have been detected in several granite-endemic species within Western Australia (Byrne and Hopper 2008; Butcher et al. 2009; Tapper et al. 2014). Specifically, high levels of genetic differentiation have been reported in several congeneric species endemic to Karst in South China (Ni et al. 2006; Wang et al. 2013, 2017; Gao et al. 2015). These results suggest that high genetic differentiation may be an inherent characteristic for edaphic island specialist, which could be due to strong geographical isolation, genetic drift, and/or environmental selection.

Geographic Isolation and Genetic Drift

Geographic isolation coupled with small population size should lead to a reduction in genetic variation due to decrease in gene flow and random genetic drift. We observed particularly low levels of diversity in the extremely spatially isolated populations of P. juliae. Such a loss of genetic diversity may reflect the effects of limited gene flow and genetic drift. Consistent with the trend of population geographic proximity detected in population structure, both Mantel tests and RDA analysis indicated that an IBD pattern explains a significant amount of genetic variation. Additionally, migration events were mainly detected among nearby populations belonging to central and southern groups (fig. 2). In addition to natural barriers to dispersal such as the Nanling Mountain ridge in Karst and Danxia landscapes, there are many open spaces with normal soil types among populations unsuitable for Primulina. The scale of natural dispersal in Primulina may be limited, owing to both the tiny seeds without specific dispersal mechanisms, and the severely insular nature of these populations. Therefore, geographic isolation and limited dispersal capability could act as components of the “insular syndrome,” as found in some island animal species (Adler and Levins 1994; Bertrand et al. 2014; Szulkin et al. 2016).

Several other lines of evidence further suggest that strong genetic drift may have contributed to population differentiation by randomly fixing alleles, resulting in significantly high F_ST values detected in both pairwise comparisons among populations and in the global analysis (table 2). First, all P. juliae populations have extremely low effective population sizes (N_E), and overwhelming genetic signatures of historical bottlenecks. Second, the magnitude of genetic drift in P. juliae is more than ten times larger than a congeneric species, P. eburnea, and increases with the degree of spatial isolation, as evidenced by much stronger genetic drift detected in the three extremely spatially isolated populations. Overall, the combined evidence of a significant IBD pattern, together with low genetic diversity, extremely low effective population sizes, and genetic signatures of drift and historical bottlenecks, suggest that geographic isolation and genetic drift are the critical evolutionary forces driving genetic differentiation among P. juliae populations, which is consistent with the findings in other plants endemic to terrestrial island-like habitats (Gao et al. 2015).

Environmental Adaptation

The roles of IBD and IBE in natural systems have been intensively investigated with meta-analyses (Orsini et al. 2013; Shafer and Wolf 2013; Sexton et al. 2014) and all identify multiple examples of IBE, highlighting the importance of environmental adaptation driving patterns of genetic differentiation. Our results based on separate IBE analyses indicated a significant effect of environment distances in climatic factors on genetic differentiation of P. juliae, while the effect of edaphic types seems to be minimal. As environmental dissimilarity and geographic distance among populations are often correlated, disentangling the relative effects of geography and environment on population genetic differentiation is critical to examining IBE (Shafer and Wolf 2013). RDA analysis enables identification and testing of the effect of individual variables influencing genomic variability, while also offering the potential to detect collinearity between them (Lasky et al. 2012). Our RDA results indicated that environment is a better predictor of genetic differentiation than geography, with 19.9% and 14.7% of differentiation being explained by environment and geography, respectively (fig. 4B). Specifically, both climatic factors and soil types shaped a significant proportion of genomic variation, suggesting that microgeographic adaptation might have played an important role in P. juliae.

RAD-based population genomic analyses allow for the identification of loci potentially under selection by scanning thousands of markers across the genome (Orsini et al. 2013; Manthey and Moyle 2015). Despite the increasing accessibility of large numbers of markers for nonmodel taxa, positive selection may still be conflated with demographic fluctuations because they leave similar signals in genomic variation (Currat 2006; Bragg et al. 2015). Recently, several studies have evaluated the effect of demographic history on the performance of different outlier test methods (De Mita et al. 2013; Lotterhos and Whitlock 2014; Hoban et al. 2016). As genetic drift tends to increase differentiation among populations, which seems to be the scenario in P. juliae, outlier methods based on F_ST values have limited power to detect positive selection under strong genetic drift, as demonstrated by De Mita et al. (2013). Indeed, our outlier analysis with BayeScan failed to find any locus experiencing positive selection among populations, while one locus was detected between habitats. BayPass allows a more robust identification of highly differentiated SNPs based on a calibration procedure of the XtX statistic (Günther and Coop 2013) by correcting for confounding demographic effects, and has been shown to have high efficiency compared to other genome scan methods (Gautier 2015). With this method, 19 loci were detected to be under positive selection pressure, in addition to the same locus as detected with BayeScan analysis when comparing two habitats, indicating that divergent selection may have contributed to differentiation despite strong genetic drift in P. juliae. Additionally, environment-associated SNPs may reflect the impact of local adaptation, which has been implicated in other recent studies (De Mita et al. 2013; Bragg et al. 2015; Lasky et al. 2015; Francois et al. 2016). The identified loci associated with variation in climatic factors or soil types (supplementary table S2, Supplementary Material online) further suggest the existence of adaptive divergence among P. juliae populations. It should be noted that the small sampling size (n = 5–8 per population) may lower the power to detect rare alleles. However, given that the extant population sizes of P. juliae are generally small, our sampling strategies have indeed met the critical requirement of optimal design for such studies, including considering the geographic scale at which local adaptation occurs and sampling many populations rather than many individuals per population (De Mita et al. 2013; Hoban et al. 2016).

An important question that needs continued attention is whether adaptation results from local selection against maladapted genotypes through climatic factors or aspects of habitats such as soils. Integrating habitat, climatic, and genetic data can begin to clarify this issue. RDA analyses confirmed that genomic differentiation in P. juliae was significantly driven by both habitat types and climatic factors, independent of geography (table 3; fig. 4B). However, the effect of habitat types is much smaller than climatic factors. Nevertheless, we identified several candidate loci involved in metal ion binding, calcium ion binding, DNA damage/repair, biosynthetic process, and metabolic process (supplementary table S2, Supplementary Material online), which would be critically important for P. juliae to adapt to special edaphic habitats with high mineral ion concentrations and lack of water. Nine loci were found significantly associated with habitat type, providing further evidence for edaphic adaptation. Specifically, enrichment analysis highlighted some genes that fit well with observed elemental challenges at such special edaphic habitats. For example, the A. thaliana ortholog AT3G57330 encodes for protein ACA11, which is involved in Ca²⁺ signaling and Ca²⁺ homeostasis in the vacuole, a major Ca²⁺ storage compartment in plant cells (Lee et al. 2007). Such findings associated with special edaphic adaptation seem to be similar to the “serpentine syndrome” detected in Arabidopsis lyrata, Arabidopsis arenosa, and Alyssum serpyllifolium, with many of the identified gene categories associated with observed elemental characteristics of low K and S, high Mg, low Ca: Mg ratios, and high Ni on serpentine outcroppings (Turner et al. 2008, 2010; Arnold 2016; Sobczyk et al. 2017).

Our results support a slightly more important role of environmental adaptation than geographic factors as evolutionary forces driving population differentiation. It is possible that geographic isolation induces initial differentiation, then divergent selection from edaphic and climatic factors would further reinforce and accumulate the population genetic differentiation, as evidenced in terrestrial mountain islands insect Pseudovelia (Ye et al. 2016). This conclusion is different from a scenario of strictly nonadaptive evolution hypothesis of P. eburnea complex and Begonia in karst regions in southern China (Chung et al. 2014; Gao et al. 2015). Another study on species of Primulina indicated a high degree of nutrient heterogeneity in soils and lack of phylogenetic signal in this genus related to soil chemistry. This study suggests that these species might have adapted to the local conditions of their microhabitats via divergent selection (Hao et al. 2015). The authors further demonstrated that the variation in elemental concentrations of leaf Ca and P could be largely attributed to effects of climatic and soil conditions (Hao et al. 2015). Similarly, a significant positive relationship was detected between genome size and latitude, highlighting signal of adaptive evolution in Primulina (Kang et al. 2014). In agreement with our results, genetic adaptation has been reported in many edaphic specialists. For example, population resequencing revealed local adaptation to serpentine soils in A. lyrata (Turner et al. 2010). More recently, highly localized selective sweeps associated with serpentine adaptation have been demonstrated in autotetraploid A. arenosa (Arnold 2016). Similarly, a broadly conserved genetic basis for trichome variation was found associated with thermal and nonthermal edaphic adaption in Mimulus guttatus (Hendrick et al. 2016). It seems that local adaptation could be a common scenario for edaphic specialists. However, it is difficult to detect a signature of positive selection with traditional F_ST-based methods due to the high genetic differentiation associated with such terrestrial islands. Additionally, the reduced-representation sequencing methods have some inherent limitation to capture neutral or adaptive genetic variation at the genome level. In particular, these methods may not uncover low frequency alleles that may be significant for adaptation and demographic processes. Therefore, complementary studies including genomic scanning by correcting for confounding demographic effects, estimating the relative contribution of each predictor simultaneously with RDA and using whole genome re-sequencing methods would be critically useful.

Conclusion

Our study demonstrates that the population divergence in P. juliae was the complementary result of both neutral drift and natural selection pressures, building on previous studies that have emphasized only the role of geographic isolation and neutral drift in driving population differentiation in Karst endemic species (Gao et al. 2015). Specifically, environment is a more important predictor of genetic differentiation than geography, indicating a predominant role of environmental adaptation in this species. Indeed, our field investigation found that P. juliae shows great phenotypic variation across its distribution range (M. Kang, unpublished data), which could be an indicative of local adaptation. More importantly, our study suggests that both soil types and climatic factors may have contributed to patterns of genetic variation of P. juliae, highlighting the importance of microgeographic adaptation in this species.

Supplementary Material

Supplementary data are available at Genome Biology and Evolution online.