The Evolution of Gene-Specific Transcriptional Noise Is Driven by Selection at the Pathway Level

Gene expression is a noisy process: in constant environment and genotype, cell to cell variability occurs because of randomness of biochemical reactions...

Abstract

Biochemical reactions within individual cells result from the interactions of molecules, typically in small numbers. Consequently, the inherent stochasticity of binding and diffusion processes generates noise along the cascade that leads to the synthesis of a protein from its encoding gene. As a result, isogenic cell populations display phenotypic variability even in homogeneous environments. The extent and consequences of this stochastic gene expression have only recently been assessed on a genome-wide scale, owing, in particular, to the advent of single-cell transcriptomics. However, the evolutionary forces shaping this stochasticity have yet to be unraveled. Here, we take advantage of two recently published data sets for the single-cell transcriptome of the domestic mouse Mus musculus to characterize the effect of natural selection on gene-specific transcriptional stochasticity. We show that noise levels in the mRNA distributions (also known as transcriptional noise) significantly correlate with three-dimensional nuclear domain organization, evolutionary constraints on the encoded protein, and gene age. However, the position of the encoded protein in a biological pathway is the main factor that explains observed levels of transcriptional noise, in agreement with models of noise propagation within gene networks. Because transcriptional noise is under widespread selection, we argue that it constitutes an important component of the phenotype and that variance of expression is a potential target of adaptation. Stochastic gene expression should therefore be considered together with the mean expression level in functional and evolutionary studies of gene expression.

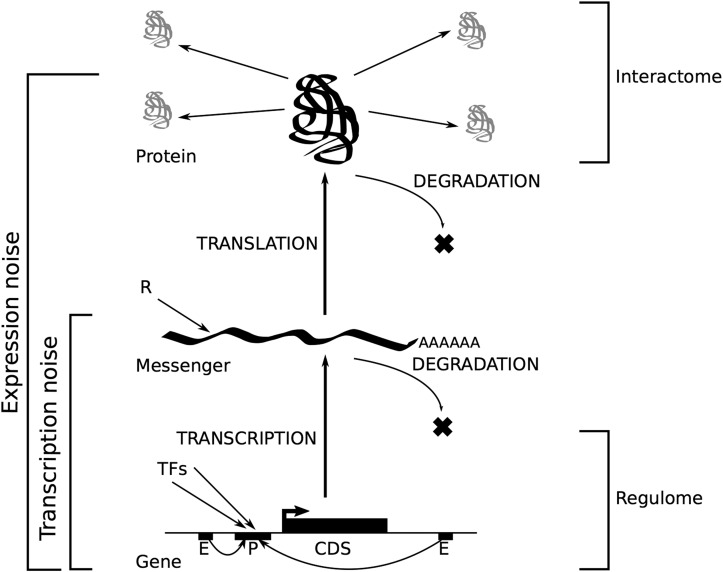
ISOGENIC cell populations display phenotypic variability even in homogeneous environments (Spudich and Koshland 1976). This observation challenged the clockwork view of the intracellular molecular machinery and led to the recognition of the stochastic nature of gene expression. Since biochemical reactions result from the interactions of individual molecules in small numbers (Gillespie 1977), the inherent stochasticity of binding and diffusion processes generates noise along the biochemical cascade leading to the synthesis of a protein from its encoding gene (Figure 1). The study of stochastic gene expression (SGE) classically recognizes two sources of expression noise. Following the definition introduced by Elowitz et al. (2002), extrinsic noise results from variation in the concentration, state, and location of shared key molecules involved in the reaction cascade from transcription initiation to protein folding. This is because molecules that are shared among genes, such as ribosomes and RNA polymerases, are typically present in low copy numbers relative to the number of genes that are actively transcribed (Shahrezaei and Swain 2008). Extrinsic factors also include physical properties of the cell such as size and growth rate, which are likely to impact the diffusion process of all molecular players. Extrinsic factors therefore affect every gene in a cell equally. Conversely, intrinsic factors generate noise in a gene-specific manner. They involve, for example, the strength of cis-regulatory elements (Suter et al. 2011), as well as the stability of the mRNA molecules that are transcribed (McAdams and Arkin 1997; Thattai and Oudenaarden 2001). Every gene is affected by both sources of stochasticity and the relative importance of each has been discussed in the literature (Becskei et al. 2005; Raj and Oudenaarden 2008). Shahrezaei and Swain (2008) proposed a more general, systemic definition for any organization level, where intrinsic stochasticity is “generated by the dynamics of the system from the random timing of individual reactions” and extrinsic stochasticity is “generated by the system interacting with other stochastic systems in the cell or its environment.” This generic definition therefore includes Raser and O’Shea’s suggestion to further distinguish extrinsic noise occurring “within pathways” and “between pathways” (Raser and O’Shea 2005). Other organization levels of gene expression are also likely to affect expression noise, such as chromatin structure (Blake et al. 2003; Hebenstreit 2013) and three-dimensional (3D) genome organization (Pombo and Dillon 2015).

Figure 1.

A systemic view of gene expression. CDS, coding sequence; TFs, transcription factors.

Pioneering work by Fraser et al. (2004) has shown that SGE is an evolvable trait that is subject to natural selection. First, genes involved in core functions of the cell are expected to behave more deterministically (Barkai and Leibler 1999) because temporal oscillations in the concentration of their encoded proteins are likely to have a deleterious effect. Second, genes involved in the immune response (Arkin et al. 1998; Norman et al. 2015) and responses to environmental conditions can benefit from being unpredictably expressed in the context of selection for bet-hedging (Thattai and Oudenaarden 2004). As the relationship between fitness and stochasticity depends on the function of the underlying gene, selection on SGE is expected to act mostly at the intrinsic level (Newman et al. 2006; Lehner 2008; Wang and Zhang 2011). However, the molecular mechanisms by which natural selection operates to regulate expression noise remain to be elucidated.

Due to methodological limitations, seminal studies on SGE (both at the mRNA and protein levels) have focused on only a handful of genes (Elowitz et al. 2002; Ozbudak et al. 2002; Chubb et al. 2006). The canonical approach consists of selecting genes of interest and recording the change of their noise levels in a population of clonal cells as a function of either: (1) the concentration of the molecule that controls the affinity of the transcription factor (TF) to the promoter region of the gene (Blake et al. 2003; Bar-Even et al. 2006) or (2) mutations artificially imposed in regulatory sequences (Ozbudak et al. 2002). In parallel with theoretical work (Kepler and Elston 2001; Batada and Hurst 2007; Kaufmann and van Oudenaarden 2007; Sánchez and Kondev 2008), these pioneering studies have provided the basis of our current understanding of the proximate molecular mechanisms behind SGE, namely complex regulation by TFs, architecture of the upstream region (including the presence of the TATA box), gene orientation (Wang et al. 2011), translation efficiency, mRNA/protein stability (Eldar and Elowitz 2010), and properties of the protein–protein interaction (PPI) network (Li et al. 2010). However, measurements at the genome scale coupled with rigorous statistical analyses are needed to go beyond gene idiosyncrasies and particular histories, and test hypotheses about the evolutionary forces shaping SGE (Sauer et al. 2007).

The recent advent of single-cell RNA sequencing makes it possible to sequence the transcriptome of each individual cell in a collection of clones, and to observe the variation of gene-specific mRNA quantities across cells. This provides a genome-wide assessment of transcriptional noise. While not accounting for putative noise resulting from the process of translation of mRNAs into proteins, transcriptional noise accounts for noise generated by both the synthesis and degradation of mRNA molecules (Figure 1). However, previous studies have shown that transcription is a limiting step in gene expression and that transcriptional noise is therefore a good proxy for expression noise (Newman et al. 2006; Taniguchi et al. 2011). Here, we used publicly available single-cell transcriptomics data sets to quantify gene-specific transcriptional noise and relate it to other genomic factors to uncover the molecular basis of selection on SGE.

Materials and Methods

Single-cell gene expression data set

We used the data set generated by Sasagawa et al. (2013) retrieved from the Gene Expression Omnibus repository (accession number GSE42268). We analyzed expression data corresponding to embryonic stem cells (ESC) in G1 phase, for which more individual cells were sequenced. A total of 17,063 genes had non-zero expression in at least one of the 20 single cells. Similar to Shalek et al. (2014), a filtering procedure was performed where only genes whose expression level satisfied log[fragments per kilobase of transcripts per million mapped fragments (FPKM) + 1] >1.5 in at least one single cell were kept for further analyses. This filtering step resulted in a total of 13,660 appreciably expressed genes for which transcriptional noise was evaluated.

Measure of transcriptional noise

The expression mean ($\mu$) and variance (${\sigma }^2$) of each gene over all single cells were computed. We measured SGE as the ratio $F^{\ast }={\sigma }^2/\widehat{{\sigma }^2\left(\mu \right)},$ where $\widehat{{\sigma }^2\left(\mu \right)}$ is the expected variance given the mean expression. To compute $\widehat{{\sigma }^2\left(\mu \right)},$ we performed several polynomial regressions with $log\left({\sigma }^2\right)$ as a function of $log\left(\mu \right),$ with degrees between 1 and 5. We then tested the resulting F* measures for residual correlation with mean expression using Kendall’s rank correlation test. We find that a degree 3 polynomial regression was sufficient to remove any residual correlation with F* (Kendall’s τ = 0.0037, P-value = 0.5217). F* can be seen as a general expression for the Fano factor and noise measure: when using a polynome of degree 1, the expression of F* becomes $F^{\ast }={\sigma }^2/exp\left(a+b.log\left(\mu \right)\right)={\sigma }^2/exp\left(a\right).{\mu }^b,$ and is therefore equivalent to the Fano factor when a = 0 and b = 1, and equivalent to noise when a = 0 and b = 2.

Genome architecture

The mouse proteome from Ensembl (genome version: mm9) was used to get coordinates of all genes. The Hi-C data set for ESCs from Dixon et al. (2012) was used to get 3D domain information. Two genes were considered in proximity in one dimension (1D) if they are on the same chromosome and no protein-coding gene was found between them. The primary distance (in number of nucleotides) between their midpoint coordinates was also recorded as 1D a distance measure between the genes. Two genes were considered in proximity in 3D if the normalized contact number between the two windows that the genes belonged to was non-null. Two genes belonging to the same window were considered to be in proximity. We further computed the relative difference of SGE between two genes by computing the ratio $\left(F_2^{\ast }-F_1^{\ast }\right)/\left(F_2^{\ast }+F_1^{\ast }\right).$ For each chromosome, we independently tested whether there was a correlation between the primary distance and the relative difference in SGE with a Mantel test, as implemented in the ade4 package (Dray and Dufour 2007). To test whether genes in proximity (1D and 3D) had more similar transcriptional noise than distant genes, we contrasted the relative differences in transcription noise between pairs of genes in proximity and pairs of distant genes. As we test all pairs of genes, we performed a randomization procedure to assess the significance of the observed differences by permuting the rows and columns in the proximity matrices 10,000 times. Linear models accounting for “spatial” interactions with genes were fitted using the generalized least squares (GLS) procedure, as implemented in the nlme package for R. A correlation matrix between all tested genes was defined as $G=\left\{g_{i,j}\right\},$ where $g_{i,j}$ is the correlation between genes i and j. We defined $g_{i,j}=1-exp\left(-\lambda {\delta }_{i,j}\right),$ where ${\delta }_{i,j}$ takes 1 if genes i and j are in proximity, and 0 otherwise (binary model). Alternatively, ${\delta }_{i,j}$ can be defined as the actual number of contacts between the two 20-kb regions [as defined by Dixon et al. (2012)] to which the genes belong (proportional model). Parameter $\lambda$ was estimated jointly with other model parameters, it measures the strength of the genome spatial correlation. Models were compared using Akaike’s information criterion (AIC). We find that the proportional correlation model fitted the data better and therefore selected it for further analyses.

TFs and histone marks

TF mapping data from the Ensembl regulatory build (Zerbino et al. 2015) were obtained via the biomaRt package for R. We used the Grch37 build as it contained data for stem cell epigenomes. Genes were considered to be associated with a given TF when at least one binding evidence was present in the 3-kb upstream flanking region. TFs associated with more than five genes for which transcriptional noise could be computed were not considered further. A similar mapping was performed for histone marks by counting the evidence of histone modifications in the 3-kb upstream and downstream regions of each gene. A logistic principal component analysis (PCA) was conducted on the resulting binary contingency tables using the logisticPCA package for R (Landgraf and Lee 2015), for TF and histone marks separately. Principal components (PCs) were used to define synthetic variables for further analyses.

Biological pathways, PPIs, and network topology

We defined genes either in the top 10% least noisy or in the top 10% most noisy as candidate sets, and used the Reactome PA package (Yu and He 2016) to search the mouse Reactome database for overrepresented pathways with a 1% false discovery rate (FDR).

Centrality measures were computed using a combination of the igraph (Csardi and Nepusz 2006) and graphite (Sales et al. 2012) packages for R. As the calculation of assortativity does not handle missing data (that is, nodes of the pathway for which no value could be computed), we computed assortativity on the subnetwork with nodes for which data were available. Reactome centrality measures could be computed for a total of 4454 genes with expression data.

PPIs were retrieved from the iRefIndex database (Razick et al. 2008) using the iRefR package for R (Mora and Donaldson 2011). Interactions were converted to a graph using the dedicated R functions in the package, and the same methods were used to compute centrality measures as for the pathway analysis. Because the PPI-based graph was not oriented, authority scores were not computed for this data (as this gave identical results to hub scores). Furthermore, as most genes are part of a single graph structure in the case of PPIs, closeness values were not further analyzed as they were virtually identical for all genes.

Gene ontology enrichment

Of the 13,660 genes, 8325 were associated with Gene Ontology (GO) terms. We tested genes for GO term enrichment at both ends of the F* spectrum using the same threshold percentile of 10% low/high-noise genes as we did for the Reactome analysis. We carried out GO enrichment analyses using two different algorithms implemented in the /topGO/ R package.: “Parent-child” (Grossmann et al. 2007) and “Weight01,” a mixture of two algorithms developed by Alexa et al. (2006). We kept only the terms that appeared simultaneously on both Parent-child and Weight01 at under a 1% significance level, controlling for multiple testing using the FDR method (Benjamini and Hochberg 1995).

Sequence divergence

Ensembl’s Biomart interface was used to retrieve the proportion of nonsynonymous (Ka) and synonymous (Ks) divergence estimates for each mouse gene relative to the human ortholog. This information was available for 13,124 genes.

Gene age

The relative taxonomic ages of the mouse genes have been computed and are available in the form of 20 phylostrata (Neme and Tautz 2013). Each phylostratum corresponds to a node in the phylogenetic tree of life. Phylostratum 1 corresponds to “All cellular organisms” whereas phylostratum 20 corresponds to “Mus musculus,” with other levels in between. We used this published information to assign each of our genes to a specific phylostratum and used this as a relative measure of gene age: Age = 21 − phylostratum, so that an age of 1 corresponds to genes specific to M. musculus and genes with an age of 20 are found in all cellular organisms.

Linear modeling

We simultaneously assessed the effect of different factors on transcriptional noise by fitting linear models to the gene-specific F* estimates. To avoid colinearity issues of intrinsically correlated explanatory variables, we conducted a data reduction procedure using multivariate analysis. We used variants of PCA on explanatory variables in three groups: network centrality measures, Ka/Ks and gene age with standard PCA, and TF-binding evidence and histone methylation patterns using logistic PCA, a generalization of PCA for binary variables (Landgraf and Lee 2015). In each case, we used the most representative components (totaling ≥75% of the total deviance) as synthetic variables. PCA analysis was conducted using the ade4 package for R (Dray and Dufour 2007) and logistic PCA was performed using the logisticPCA package (Landgraf and Lee 2015).

We built a linear model with F* as a response variable and 13 synthetic variables as explanatory variables. As the synthetic variables are PCs, they are orthogonal by construction. The fitted model displayed a significant departure to normality and was further transformed using the Box-Cox procedure [“boxcox” function from the MASS package for R (Venables and Ripley 2002)]. Residues of the selected model had normal, independent residue distributions (Shapiro–Wilk test of normality, P-value = 0.121; Ljung–Box test of independence, P-value = 0.2061) but still displayed significant heteroscedasticity (Harrison–McCabe test, P-value = 0.003). To ensure that this departure from the Gauss–Markov assumptions does not bias our inference, we used the “robcov” function of the rms package to get robust estimates of the effect significativity (Harrell 2015). The relative importance of each explanatory factor was assessed using the method of Lindeman, Merenda, and Gold (Lindeman et al. 1979), as implemented is the R package relaimpo. The significance of the level of variance explained by each factor was computed using a standard ANOVA procedure.

Additional data sets

The aforementioned analyses were additionally conducted on the bone marrow-derived dendritic cell (BMDC) data set of Shalek et al. (2014). Following the filtering procedure established by the authors in the original paper, genes that did not satisfied the condition of being expressed by an amount such that log(TPM + 1) > 1 in at least one of the 95 single cells were further discarded, where TPM stands for transcripts per million. This cut-off threshold resulted in 11,640 genes being kept for investigation. The rest of the analyses were conducted in the same way as for the ESC data set.

Jackknife procedure

A jackknife procedure was conducted to assess: (1) the robustness of our results to the choice of actual cells used to estimate mean and variance in gene expression and (2) the power of the pooled RNA sequencing analysis for which only three replicates were available. This analysis was conducted by sampling 3, 5, 10, and 15 of the original 20 single cells of the ESC data set (Sasagawa et al. 2013), 1000 times in each case. The exact same analysis was conducted on each random sample as for the complete data set, and model coefficients and their associated P-values were recorded.

Data availability

All data sets and scripts to reproduce the results of this study are available under the DOI 10.6084/m9.figshare.4587169.

Results

A new measure of noise to study genome-wide patterns of SGE

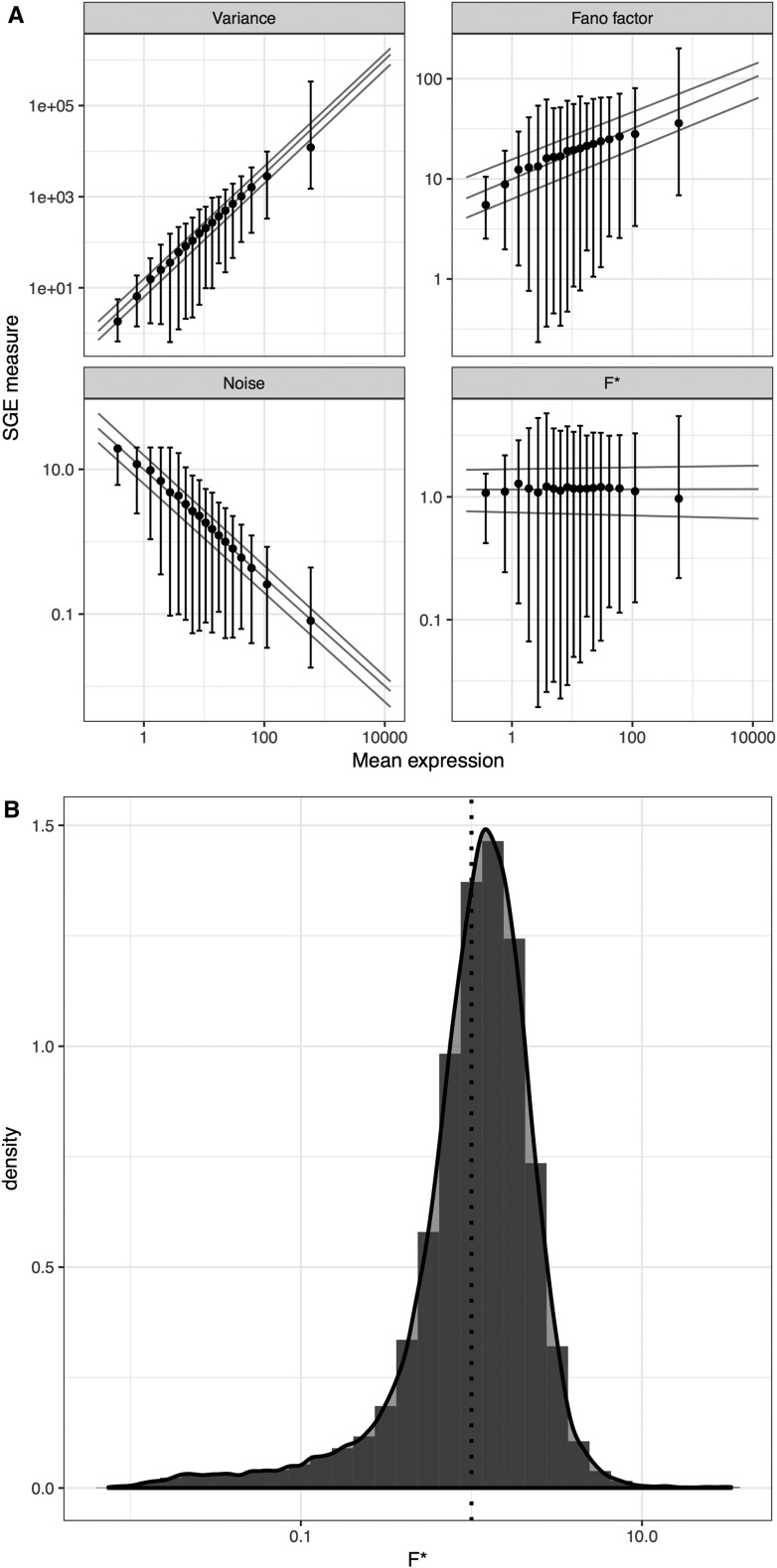
We used the data set generated by Sasagawa et al. (2013), which quantifies gene-specific amounts of mRNA as FPKM values for each gene and each individual cell. Among these, we selected all genes in a subset containing 20 ESCs in G1 phase to avoid recording variance that is due to different cell types or cell-cycle phases. The Quartz-Seq sequencing protocol captures every poly-A RNA present in the cell at one specific moment, allowing the assessment of transcriptional noise. Following Shalek et al. (2014), we first filtered out genes that were not appreciably expressed to reduce the contribution of “technical” noise to the total noise. For each gene, we further calculated the mean μ in FPKM units and variance ${\sigma }^2$ in FPKM² units, as well as two previously published measures of stochasticity: the Fano factor, usually referred to as the bursty parameter, defined as ${\sigma }^2/\mu$, and noise, defined as the coefficient of variation squared (${\sigma }^2/{\mu }^2$). Both the variance and Fano factor are monotonically increasing functions of the mean (Figure 2A). Noise is inversely related to mean expression (Figure 2A), in agreement with previous observations at the protein level (Bar-Even et al. 2006; Taniguchi et al. 2011). While this negative correlation was theoretically predicted (Tao et al. 2007), it may confound the analyses of transcriptional noise at the genome level, because mean gene expression is under specific selective pressure (Pál et al. 2001). To disentangle these effects, we developed a new quantitative measure of noise, independent of the mean expression level of each gene. To achieve this, we performed polynomial regressions in the log-space plot of variance vs. mean. We defined F* as ${\sigma }_{obs}^2/{\sigma }_{pred}^2$ (see Materials and Methods), that is, the ratio of the observed variance over the variance component predicted by the mean expression level. We selected the simplest model for which no correlation between F* and mean expression was observed, and found that a degree 3 polynomial model was sufficient to remove further correlation (Kendall’s τ = −0.0037, P-value = 0.5217, Figure 2A). Genes with F* < 1 have a variance lower than expected according to their mean expression, whereas genes with F* > 1 behave the opposite way (Figure 2B). This approach fulfills the same goal as the running median approach of Newman et al. (2006), while it includes the effect of mean expression directly into the measure of stochasticity instead of correcting a posteriori a dependent measure (in that case, the Fano factor). We therefore use F* as a measure of SGE throughout this study.

Figure 2.

Transcriptional noise and mean gene expression. (A) Measures of noise plotted against the mean gene expression for each gene, in logarithmic scales: Variance, Fano factor (variance/mean), noise (square of the coefficient of variation, variance/mean²), and F* (this study). Lines represent quantile regression fits (median, first, and third quartiles). Point and bars represent median, first, and third quartiles for each category of mean expression obtained by discretization of the x-axis. (B) Distribution of F* over all genes in this study. Vertical line corresponds to F* = 1. SGE, stochastic gene expression.

SGE correlates with the 3D structure of the genome

We first sought to investigate whether genome organization significantly impacts the patterns of SGE. We assessed whether genes in proximity along chromosomes display more similar amounts of transcriptional noise than distant genes. We tested this hypothesis by computing the primary distance on the genome between each pair of genes, that is, the number of base pairs separating them on the chromosome, as well as the relative difference in their transcriptional noise (see Materials and Methods). We found no significant association between the two distances (Mantel tests, each chromosome tested independently). However, contiguous genes had significantly more similar transcriptional noise that noncontiguous genes (permutation test, P-value < 1 × 10⁻⁰⁴, Figure S1). Using Hi-C data from mouse embryonic cells (Dixon et al. 2012), we report that genes in contact in three dimensions have significantly more similar transcriptional noise than genes not in contact (permutation test, P-value < 1 × 10⁻⁰³, Figure S1). Most contiguous genes in one dimension also appear to be close in three dimensions, and the effect of 3D contact is stronger than that of 1D contact. These results therefore suggest that the 3D structure of the genome has a stronger impact on SGE than the position of the genes along the chromosomes. We further note that while highly significant, the size of this effect is small, with a mean difference in relative expression of −1.10% (Figure S1).

TF binding and histone methylation impact SGE

The binding of TFs to promoters constitutes one notable source of transcriptional noise (Figure 1) (Blake et al. 2003; Newman et al. 2006). In eukaryotes, the accessibility of promoters is determined by the chromatin state, which is itself controlled by histone methylation. We assessed the extent to which transcriptional noise is linked to particular TFs and histone marks by using data from the Ensembl regulatory build (Zerbino et al. 2015), which summarizes experimental evidence of TF binding and methylation sites along the genome. First, we contrasted the F* values of genes with binding evidence for each annotated TF independently. Among 13 TFs represented by at least five genes in our data set, we found that four of them significantly influence F* after adjusting for a global FDR of 5%: the transcription repressor CTFC (adjusted P-value = 0.0321), the TF CP2-like 1 (Tcfcp2l1, adjusted P-value = 0.0087), the X-linked Zinc Finger Protein (Zfx, adjusted P-value = 0.0284), and the Myc TF (MYC, adjusted P-value = 0.0104). Interestingly, association with each of these four TFs led to an increase in transcriptional noise. We also report a weak but significant positive correlation between the number of TFs associated with each gene and the amount of transcriptional noise (Kendall’s τ = 0.0238, P-value = 0.0007). This observation is consistent with the idea that noise generated by each TF is cumulative (Sharon et al. 2014). We then tested if particular histone marks are associated with transcriptional noise. Among five histone marks represented in our data set, three were found to be highly significantly associated to a higher transcriptional noise: H3K4me3 (adjusted P-value = 2.0 × 10⁻¹⁴⁶), H3K4me2 (adjusted P-value = 5.5 × 10⁻¹²¹), and H3K27me3 (adjusted P-value = 5.3 × 10⁻³⁴). Methylation on the fourth lysine of histone H3 is associated with gene activation in humans, while trimethylation on lysine 27 is usually associated with gene repression (Barski et al. 2007). These results suggest that both gene activation and silencing contribute to the stochasticity of gene expression, in agreement with the view that bursty transcription leads to increased noise (Blake et al. 2003; Newman et al. 2006; Batada and Hurst 2007).

Low noise genes are enriched for housekeeping functions

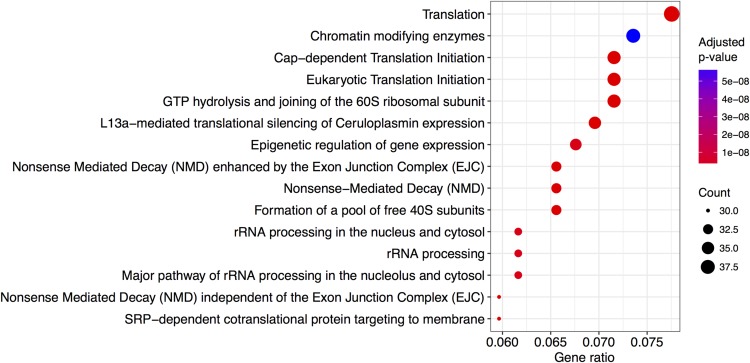
We investigated the function of genes at both ends of the F* spectrum. We defined as candidate gene sets the top 10% least noisy or the top 10% most noisy genes in our data set, and tested for enrichment of GO terms and Reactome pathways (see Materials and Methods). It is expected that genes encoding proteins participating in housekeeping pathways are less noisy because fluctuations in the concentrations of their products might have stronger deleterious effects (Pedraza and van Oudenaarden 2005). On the other hand, SGE could be selectively advantageous for genes involved in immune and stress responses, as part of a bet-hedging strategy (e.g., Arkin et al. 1998; Shalek et al. 2013). A GO terms enrichment test revealed significant categories enriched in the low-noise gene set only: molecular functions “nucleic acid binding” and “structural constituent of ribosome;” the biological processes “nucleosome assembly,” “innate immune response in mucosa,” and “translation;” and the cellular component “cytosolic large ribosomal subunit” (Table 1). All these terms but one relate to gene expression, in agreement with previously reported findings in yeast (Newman et al. 2006). We further find a total of 41 Reactome pathways significantly overrepresented in the low-noise gene set (FDR set to 1%). Interestingly, the most significant pathways belong to modules related to translation (RNA processing, initiation of translation, and ribosomal assembly), as well as several modules relating to gene expression, including chromatin regulation and mRNA splicing (Figure 3). Only one pathway was found to be enriched in the high-noise set: TP53 regulation of transcription of cell cycle genes (P-value = 0.0079). This finding is interesting because TP53 is a central regulator of the stress response in the cell (Hussain and Harris 2006). These results therefore corroborate previous findings that genes involved in the stress response might be evolving under selection for high noise as part of a bet-hedging strategy (Shalek et al. 2013; Viney and Reece 2013). The small amount of significantly enriched Reactome pathways by high-noise genes can potentially be explained by the nature of the data set: as the original experiment was based on unstimulated cells, genes that directly benefit from high SGE might not be expressed under these experimental conditions.

Table 1. GO terms significantly enriched in the 10% genes with lowest transcriptional noise.

Ontology	GO ID	GO term	FDR Fisher “parent−child”	FDR Fisher “weight01”
MF	GO:0003735	Structural constituent of ribosome	2.28 × 10−07	6.81 × 10−20
MF	GO:0003676	Nucleic acid binding	8.16 × 10−06	6.06 × 10−04
BP	GO:0006412	Translation	4.08 × 10−08	7.15 × 10−12
BP	GO:0002227	Innate immune response in mucosa	6.49 × 10−04	6.22 × 10−03
CC	GO:0022625	Cytosolic large ribosomal subunit	4.48 × 10−03	1.40 × 10−12

GO, Gene Ontology; ID, identifier; FDR, False Discovery Rate; MF, Molecular Function; BP, Biological Process; CC, Cellular Compartment.

Figure 3.

Enriched pathways in the low-noise gene set. Depicted pathways are the 15 most significant in the 10% of genes with lowest transcriptional noise.

Highly connected proteins are synthesized by low-noise genes

The structure of the interaction network of proteins inside the cell can greatly impact the evolutionary dynamics of genes (Jeong et al. 2000; Barabási and Oltvai 2004). Furthermore, the contribution of each constitutive node within a given network varies. This asymmetry is largely reflected in the power-law-like degree distribution that is observed in virtually all biological networks (Barabási and Albert 1999), with a few genes displaying many connections and a majority of genes displaying only a few. The individual characteristics of each node in a network can be characterized by various measures of centrality (Newman 2003). Following previous studies on protein evolutionary rate (Fraser et al. 2002; Hahn et al. 2004; Jovelin and Phillips 2009) and PPI networks (Li et al. 2010), we asked whether, at the gene level, there is a link between the centrality of a protein and the amount of transcriptional noise. We study six centrality metrics measured on two types of network data: (1) pathway annotations from the Reactome database (Fabregat et al. 2016) and (2) PPI data from the iRefIndex database. PPI data are typically more complete (5553 genes with gene expression data) but do not include information on functional interactions. The Reactome database is based on published functional evidence, but encompasses less genes (4454 genes for which expression data are available). In addition, graphs representing PPI networks are not oriented while graphs representing Pathway annotations are, implying that distinct statistics can be computed on both types of networks.

We first estimated the pleiotropy index of each gene by counting how many different pathways the corresponding proteins are involved in. We then computed centrality measures as averages over all pathways in which each gene is involved. These measures include: (1) node degree, which corresponds to the number of other nodes a given node is directly connected with; (2) hub score, which estimates the extent to which a node links to other central nodes; (3) authority score, which estimates the importance of a node by assessing how many hubs link to it; (4) transitivity, or clustering coefficient, defined as the proportion of neighbors that also connect to each other; (5) closeness, a measure of the topological distance between a node and every other reachable node (the fewer edge hops it takes for a protein to reach every other protein in a network, the higher its closeness); and (6) betweenness, a measure of the frequency with which a protein belongs to the shortest path between every pair of nodes.

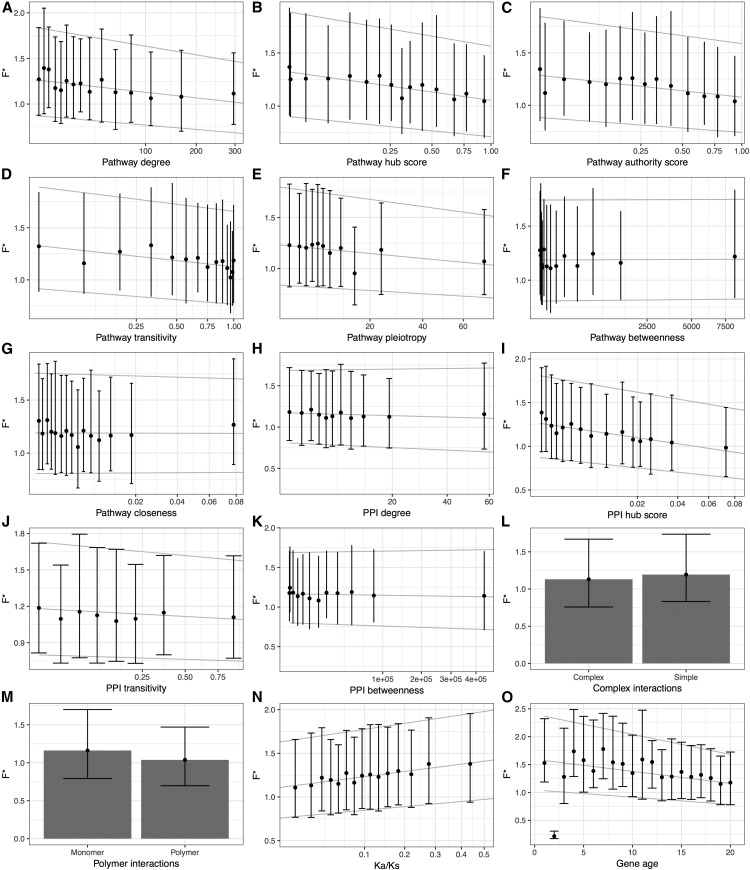
We find that node degree, hub score, authority score; and transitivity are all significantly negatively correlated with transcriptional noise on pathway-based networks: the more central a protein is, the less transcriptional noise it displays (Figure 4, A–D and Table 2). We also observed that pleiotropy is negatively correlated with F* (Kendall’s τ = −0.0514, P-value = 8.31 × 10⁻⁰⁷, Figure 4E and Table 2), suggesting that a protein that potentially performs multiple functions at the same time needs to be less noisy. As pleiotropic genes are themselves more central (e.g., correlation of pleiotropy and node degree: Kendall’s τ = 0.2215, P-value < 2.2 × 10⁻¹⁶) and evolve more slowly (correlation of pleiotropy and Ka/Ks ratio: Kendall’s τ = −0.1060, P-value < 2.2 × 10⁻¹⁶), we controlled for these variables and found consistent results (partial correlation of pleiotropy and F*, accounting for centrality measures and Ka/Ks: Kendall’s τ = −0.0254, P-value = 7.45 × 10⁻⁰⁶). Closeness and betweenness, on the other hand, show a negative correlation with F*, yet this was much less significant (Kendall’s τ = −0.0254, P-value = 0.0109 for closeness and τ = −0.0175, P-value = 0.0865 for betweenness, see Figure 4, F and G and Table 2). In modular networks (Hartwell et al. 1999), nodes that connect different modules are extremely important to the cell (Guimera and Amaral 2005) and show high betweenness scores. In yeast, high betweenness proteins tend to be older and more essential (Joy et al. 2005), an observation also supported by our data set (betweenness vs. gene age, Kendall’s τ = 0.0619, P-value = 1.09 × 10⁻⁰⁷; betweenness vs. Ka/Ks, Kendall’s τ = −0.0857, P-value = 3.83 × 10⁻¹⁶). However, it has been argued that in PPI networks, high betweenness proteins are less essential due to the lack of directed information flow, compared to, for instance, regulatory networks (Yu et al. 2007), a hypothesis that could explain the observed lack of correlation.

Figure 4.

Factors driving stochastic gene expression. Correlation of F* and all tested network centrality measures (A-G: pathway networks, H-M: protein-protein interaction networks), as well as protein conservation (Ka/Ks ratio) and gene age (N and O). Point and bars represent median, first, and third quartiles for each category of mean expression obtained by discretization of the x-axis, together with the quantile regression lines estimated on the full data set. PPI, protein–protein interaction.

Table 2. Correlation of transcriptional noise with gene centrality measures and pleiotropy, as estimated from pathway annotations and PPI networks.

Data	Measure	Correlation with F*	P-value
Pathways	Degree	−0.0745	1.14 × 10−13***
	Hub score	−0.0808	6.61 × 10−16***
	Authority score	−0.0666	2.72 × 10−11***
	Clustering coefficient	−0.0794	4.55 × 10−15***
	Closeness	−0.0254	1.09 × 10−02*
	Betweenness	−0.0175	8.65 × 10−02.
	Pleiotropy	−0.0514	8.31 × 10−07***
	Size	−0.0514	3.91 × 10−03***
	Diameter	0.0061	7.55 × 10−01 (NS)
	Global transitivity	−0.1532	3.06 × 10−17***
PPI	Degree	−0.0249	8.20 × 10−03**
	Hub score	−0.0942	< 2.2 × 10−16***
	Transitivity	−0.0338	6.24 × 10−04***
	Betweenness	−0.0140	1.31 × 10−01 (NS)

All correlations are computed using Kendall’s rank correlation test, with P-value codes defined as *** < 0.001 < ** < 0.01 < * < 0.05 < ^. < 0.1. NS, nonsignificant; PPI, protein–protein interaction.

By applying similar measures on the PPI network, we report significant negative correlations between F* and PPI centrality measures (Figure 4, H–K and Table 2). Because the PPI network is not directed, authority scores and hub scores cannot be distinguished. The results obtained with the mouse PPI interaction network are qualitatively similar to the ones obtained by Li et al. (2010) on Yeast expression data (Li et al. 2010). In addition, we further report that genes involved in complex interactions (that is, genes that interact with more than one other protein simultaneously) have reduced noise in gene expression (Wilcoxon rank test, P-value = 8.053 × 10⁻⁰⁵, Figure 4L), corroborating previous findings in Yeast (Fraser et al. 2004). Conversely, genes involved in polymeric interactions, that is, where multiple copies of the encoded protein interact with each other, did not show significantly different noise than other genes (Wilcoxon rank test, P-value = 0.0821, Figure 4M).

It was previously shown that centrality measures negatively correlate with evolutionary rate (Hahn and Kern 2004). Our results suggest that central genes are selectively constrained for their transcriptional noise, and that centrality therefore also influences the regulation of gene expression. Interestingly, it has been reported that central genes tend to be more duplicated (Vitkup et al. 2006). The authors proposed that such duplication events would have been favored as they would confer greater robustness to deleterious mutations in proteins. Our results are compatible with another nonexclusive, possible advantage: having more gene copies could reduce transcriptional noise by averaging the number of transcripts produced by each gene copy (Raser and O’Shea 2005).

Network structure impacts transcriptional noise of constitutive genes

Whereas estimators of node centrality highlight gene-specific properties inside a given network, measures at the whole-network level enable the comparison of networks with distinct properties. We computed the size, diameter, and global transitivity for each annotated network in our data set (1,364 networks, see Supplementary Material, File S1), which we compared with the average F* measure of all constitutive nodes. The size of a network is defined as its total number of nodes, while diameter is the length of the shortest path between the two most distant nodes. Transitivity is a measure of connectivity, defined as the average of all nodes’ clustering coefficients. Interestingly, while network size is positively correlated with average degree and transitivity (Kendall’s τ = 0.5880, P-value < 2.2 × 10⁻¹⁶ and Kendall’s τ = 0.1166, P-value = 1.08 × 10⁻¹⁰, respectively), diameter displays a positive correlation with average degree (Kendall’s τ = 0.2959, P-value < 2.2e−16) but a negative correlation with transitivity (Kendall’s τ = −0.0840, P-value = 2.17 × 10⁻⁰⁵). This is because diameter increases logarithmically with size, that is, the addition of new nodes to large networks does not increase the diameter as much as addition to small networks. This suggests that larger networks are relatively more compact than smaller ones, and that their constitutive nodes are therefore more connected. We find that average transcriptional noise correlates negatively with network size (Kendall’s τ = −0.0514, P-value = 0.0039), while being independent of the diameter (Kendall’s τ = 0.0061, P-value = 0.7547 see Table 3). These results are in line with the node-based analyses, and show that the more connections a network has, the less stochastic the expression of the underlying genes is. This supports the view of Raser and O’Shea (2005), that the gene-extrinsic, pathway-intrinsic level is functionally pertinent and needs to be distinguished from the globally-extrinsic level.

Table 3. Linear models of transcriptional noise with genomic and epigenomic factors.

	OLS			GLS
	Coefficient	SE	P-value	Coefficient	SE	P-value
(Intercept)	0.1612	0.0781	0.0392*	0.1665	0.0663	0.0121*
PC1	0.0390	0.0065	< 0.0001***	0.0396	0.0065	< 0.0001***
PC2	−0.0048	0.0069	0.4854	−0.0048	0.0069	0.4838
PC3	−0.0526	0.0091	< 0.0001***	−0.0518	0.0092	< 0.0001***
PC4	−0.0102	0.0097	0.2905	−0.0109	0.0100	0.2773
PC5	0.0117	0.0106	0.2713	0.0123	0.0106	0.2456
PC6	−0.0152	0.0107	0.1536	−0.0152	0.0109	0.1623
PC7	0.0210	0.0102	0.0384*	0.0211	0.0110	0.0561.
PC8	0.0100	0.0113	0.3778	0.0073	0.0114	0.5250
TFPC1	0.0028	0.0041	0.4912	0.0025	0.0034	0.4658
TFPC2	0.0025	0.0027	0.3664	0.0024	0.0026	0.3585
TFPC3	0.0032	0.0042	0.4513	0.0032	0.0037	0.3825
HistPC1	−0.0031	0.001	0.0015**	−0.0033	0.0010	0.0007***
HistPC2	−0.0027	0.0016	0.0846.	−0.0029	0.0015	0.0566.

All correlations are computed using Kendall’s rank correlation test, with P-value codes defined as *** < 0.001 < ** < 0.01 < * < 0.05 < ^. < 0.1. OLS, Ordinary Least Squares; GLS, Generalized Least Squares; Pathway PC1–8, principal components on centrality measures, protein conservation, and gene age; TFPC1–3, principal components of the logistic PCA on transcription factor binding evidence; HistPC1 and 2, principal components of the logistic PCA on histone modification marks.

We further asked whether genes with similar transcriptional noise tend to synthesize proteins that connect to each other (positive assortativity) in a given network or, on the contrary, tend to avoid each other (negative assortativity). We considered all Reactome pathways annotated to the mouse and estimated their respective F* assortativity. We found the mean assortativity to be significantly negative, with a value of −0.1384 (one sample Wilcoxon rank test, P-value < 2.2e−16), meaning that proteins with different F* values tend to connect with each other (Figure S3). Maslov and Sneppen (2002) reported a negative assortativity between hubs in PPI networks, which they hypothesized to be the result of selection for reduced vulnerability to deleterious perturbations. However, in our data set, we find the assortativity of hub scores to be significantly positive (average of 0.1221, one sample Wilcoxon rank test, P-value = 1.212 × 10⁻¹², Figure S5), although with a large distribution of assortativity values. As we showed that hub scores correlate negatively with F* (Table 2), we asked whether the assortativity of hub proteins can explain the assortativity of F*. We found a significantly positive correlation between the two assortativity measures (Kendall’s τ = 0.2581, P-value < 2.2 × 10⁻¹⁶). However, the relationship between the measures is not linear (Figure S5), suggesting a distinct relationship between hub score and F* for negative and positive hub score assortativity. Negative assortativity of hub proteins contributes to a negative assortativity of SGE (Kendall’s τ = 0.2730, P-value < 2.2 × 10⁻¹⁶), while the effect vanishes for pathways with positive hub score assortativity (Kendall’s τ = 0.0940, P-value = 3.135 × 10⁻⁰⁴). While assortativity of F* is closer to 0 for pathways with positive assortativity of hub score, we note that it is still significantly negative (average = −0.0818, one sample Wilcoxon test with P-value < 2.2 × 10⁻¹⁶). These results suggest the existence of additional constraints that act on the distribution of noisy proteins in a network.

Transcriptional noise is positively correlated with the evolutionary rate of proteins

In the yeast Saccharomyces cerevisiae, evolutionary divergence between orthologous coding sequences correlates negatively with fitness effect on knockout strains of the corresponding genes (Hirsh and Fraser 2001), demonstrating that protein functional importance is reflected in the strength of purifying selection acting on it. Fraser et al. (2004) studied transcription and translation rates of yeast genes and classified genes in distinct noise categories according to their expression strategies. They reported that essential genes display lower expression noise than the rest. Following these pioneering observations, we hypothesized that genes under strong purifying selection at the protein sequence level should also be highly constrained for their expression and therefore display a lower transcriptional noise. To test this hypothesis, we correlated F* with the ratio of Ka/Ks, as measured by sequence comparison between mouse genes and their human orthologs, after discarding genes with evidence for positive selection (n = 5). In agreement with our prediction, we report a significantly positive correlation between the Ka/Ks ratio and F* (Figure 4N, Kendall’s τ = 0.0557, P-value < 1.143 × 10⁻⁰⁵), that is, highly constrained genes (low Ka/Ks ratio) display less transcriptional noise (low F*) than fast-evolving ones. This result demonstrates that genes encoding proteins under strong purifying selection are also more constrained on their transcriptional noise.

Older genes are less noisy

Evolution of new genes was long thought to occur via duplication and modification of existing genetic material [“evolutionary tinkering,” (Jacob 1977)]. However, evidence for de novo gene emergence is becoming more and more common (Tautz and Domazet-Lošo 2011; Xie et al. 2012). De novo-created genes undergo several optimization steps, including their integration into a regulatory network (Neme and Tautz 2013). We tested whether the historical process of incorporation of new genes into pathways impacts the evolution of transcriptional noise. We used the phylostratigraphic approach of Neme and Tautz (2013), which categorizes genes into 20 strata, to compute gene age and tested for a correlation with F*. As older genes tend to be more conserved (Wolf et al. 2009), more central [according to the preferential attachment model of network growth (Jeong et al. 2000, 2001)], and more pleiotropic, we controlled for these confounding factors (Kendall’s τ = −0.0663, P-value = 1.58 × 10⁻³⁷ ; partial correlation controlling for Ka/Ks ratio, centrality measures and pleiotropy level, Figure 4O). These results suggest that older genes are more deterministically expressed while younger genes are noisier. While we cannot rule out that functional constraints not fully accounted for by the Ka/Ks ratio could at least partially explain the correlation of gene age and transcriptional noise, we hypothesize that the observed correlation results from ancient genes having acquired more complex regulation schemes through time. Such schemes include, for instance, negative feedback loops, which have been shown to stabilize gene expression and reduce expression noise (Becskei and Serrano 2000; Thattai and Oudenaarden 2001).

Position in the protein network is the main driver of transcriptional noise

To jointly assess the effect of network topology, epigenomic factors, Ka/Ks ratio, and gene age, we modeled the patterns of transcriptional noise as a function of multiple predictive factors within the linear model framework. This analysis could be performed on a set of 2794 genes for which values were available jointly for all variables. To avoid colinearity issues because some of these variables are intrinsically correlated, we performed data reduction procedures prior to modeling. For continuous variables, including pathway and PPI network variables, Ka/Ks ratio, and gene age, we conducted a PCA and used as synthetic measures the first eight PCs, explaining together > 80% of the total inertia (Figure S2A). The first PC (PC1) of the PCA analysis is associated with pathway centrality measures (degree, hub score, authority score, and transitivity, Figure S2B). The second PC (PC2) corresponds to PPI centrality measures (degree, hub score, and betweenness), while the third component (PC3) relates to gene age and Ka/Ks ratio. The fourth component (PC4) is associated with PPI complex interactions and transitivity. PC5 and PC6 are essentially associated with betweenness and closeness of the pathway network, PC7 with PPI polymeric interactions, and PC8 with pathway pleiotropy. As TFs and histone mark data are binary (presence/absence for each gene), we performed a logistic PCA for both types of variable (Landgraf and Lee 2015). For TFs, we selected the three first components (hereby denoted as TFPC), which explained 78% of deviance (Figure S3A). The loads on the first component (TFPC1) are all negative, meaning that TFPC1 captures a global correlation trend and does not discriminate between TFs. Tcfcp2l1 appears to be the TF with the highest correlation to TFPC1. The second component TFPC2 is dominated by TCFC (positive loading) and Oct4 (negative loading), while the third component TFPC3 is dominated by Esrrb (positive loading), MYC, nMyc, and E2F1 (negative loadings, Figure S3B). For histone marks, the two first components (hereby noted HistPC) explained 95% of variance and were therefore retained (Figure S4A). HistPC1 is dominated by mark H3K27me3 linked to gene repression (negative loadings), and HistPC2 by marks H3K4me1 and H3K4me3 linked to gene activation (positive loadings, Figure S4A).

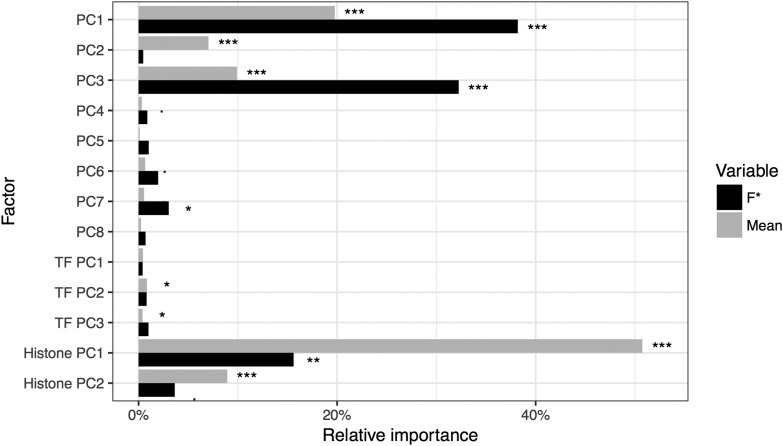
We fitted a linear model with F* as a response variable and all 13 synthetic variables as explanatory variables. We find that PC1 has a significant positive effect on F* (Table 3). As the loadings of the centrality measures on PC1 are negative (Figure S2C), this result is consistent with our finding of a negative correlation of pathway-based centrality measures with F*. PC3 has a highly significant negative effect on F*, which is consistent with a negative correlation with gene age (positive loading on PC3) and a positive correlation with the Ka/Ks ratio (negative loading on PC3, Figure S2D). The last highly significant variable is the first PC of the logistic PCA on histone methylation patterns, HistPC1, which has a negative effect on F*. Because the loadings are essentially negative on HistPC1, this suggests a positive effect of methylation, in particular the repressive H3K27me3. Altogether, the linear model with all variables explained 4.01% of the total variance (adjusted R²). This small value indicates either that gene idiosyncrasies largely predominate over general effects, or that our estimates of transcriptional noise have a large measurement error, or both. To compare the individual effects of each explanatory variable, we conducted a relative importance analysis. As a mean of comparison, we fitted a similar model with mean expression as a response variable. We find that pathway centrality measures (PC1 variable) account for 38% of the explained variance, while protein constraints and gene age (PC3) account for 32%. Chromatin state (HistPC1) accounts for another 15% of the variance (Figure 5). These results contrast with the model of mean expression, where HistPC1 and HistPC2 account for 51 and 9% of the explained variance, respectively, and PC1 and PC3 20 and 10% only (Figure 5). This suggests that: (1) among all factors tested, position in the protein network is the main driver of the evolution of gene-specific stochastic expression, followed by protein constraints and gene age, and (2) that different selective pressures act on the mean and cell-to-cell variability of gene expression.

Figure 5.

Relative importance of explanatory factors on mean gene expression and F*. Significance codes refer to ANOVA test of variance: *** < 0.001 < ** < 0.01 < * < 0.05 < ^. < 0.1. PC, principal component; TF, transcription factor.

We further included the effect of 3D organization of the genome to assess whether it could act as a confounding factor. We developed a correlation model that allowed for genes in contact to have correlated values of transcriptional noise. The correlation model was fitted together with the previous linear model in the GLS framework. This new model allows for one additional parameter, λ, which captures the strength of correlation due to 3D organization of the genome (see Materials and Methods). The estimate of λ was found to be 0.0016, which means that the spatial autocorrelation of transcriptional noise is low on average. This estimate is significantly higher than zero, and model comparison using AIC favors the linear model with 3D correlation (AIC = 4880.858 vs. AIC = 4890.396 for a linear model without 3D correlation). Despite the significant effect of 3D genome correlation, our results were qualitatively and quantitatively very similar to the model ignoring 3D correlation (Table 3).

Analysis of BMDCs supports the generality of the results

We assessed the reproducibility of our results by analyzing an additional single-cell transcriptomics data set of 95 unstimulated BMDCs (Shalek et al. 2014). After filtering (see Materials and Methods), the data set consisted of 11,640 genes. Using the same normalization procedure as for the ESC data set, we nonetheless report a weak but significant negative correlation between F* and mean expression, even with a degree 5 polynomial regression (−0.0459, P-value < 1.13e−13). This effect is due to cell RFKM values being extremely skewed in this data set, due to the distribution per gene. To assess the impact of the residual correlation with the mean, we computed a value of F* (noted F_R*) on a restricted data set where the variance was between one-eighth and eight times the mean (75% of all genes) using a quantile regression on the median instead of a linear regression. A second-degree polynomial quantile regression proved to be sufficient to remove the effect of mean expression (Kendall’s τ = 0.0114, P-value = 0.1125) on this restricted data set. As all results were consistent when using the F_R* and F* measures, we only discuss here results obtained with F* and refer to Supplementary Data 1 (available on FigShare under the DOI 10.6084/m9.figshare.4587169) for detailed results obtained with the F_R* measure.

We report a highly significant positive correlation between F* values measured on the 8792 genes with expression in both data sets, suggesting that cell-to-cell variance in gene expression is, to a large extent, conserved among the two cell types (Kendall’s τ = 0.1289, P-value < 2.2 × 10⁻¹⁶, Figure S6A). GO terms or Reactome pathway enrichment analyses reveal less significant but consistent terms with the ESC analysis: the high-F* gene set did not show any significantly enriched GO term or Reactome pathway (FDR set to 1%) and the low-F* gene set revealed RNA binding as a significantly enriched molecular function, as well as 21 enriched pathways (Figure S7). In agreement with results from the ESC analysis, many of the most significantly enriched pathways relate to gene expression, including translation and splicing. Interestingly, the two most significant pathways are “Vesicle-mediated transport” and “Membrane trafficking,” two essential pathways for the functioning of dendritic cells. Analyses of network centrality measures also generally showed consistent results with the ESC data set, with more central genes displaying reduced gene expression noise (Figure S6, B–N and Table S1). Quantitative differences consisted of PPI betweenness, as well as pathway closeness and betweenness being highly significantly negatively correlated with F* while they were only weakly significant or nonsignificant with the ESC data set. The only discrepancies that we report between the two data sets relate to pathway-level statistics. Pathway size appeared to be significantly positively correlated with mean F*, while it was negatively correlated on the ESC data set, yet with a comparatively higher P-value. Similarly, pathway diameter was significantly positively correlated with mean F* in the BMDC data set, while it was not significant with the ESC data. We currently have no hypothesis to explain this particular discrepancy. While these results support the generality of our observations, they also illustrate that, in detail, the fine structure of translational noise may vary in a cell type-specific manner.

We fitted linear models as for the ESC data set, with the exception that no epigenomic and 3D genome data were available for this cell type. Data reduction was performed using PCA, with the eight first PCs explaining 81% of the total deviance (Figure S8A). We report consistent results with the ESC analysis, with all major effects similar in direction and intensity, highlighting the impact of network centrality measures on expression noise (Table S2). However, with the BMDC data, the PC2, which is associated with PPI centrality measures (Figure S8B), appears to have a significant negative impact on F*, while it was not significant with the ESC data set. As the loading of the PPI centrality measures are positive on PC2, this is consistent with central genes having a lower transcriptional noise as for the pathway network metrics (Figure S8C). Relative importance analysis revealed that network centrality measures contributed most to the explained variance (48 and 21% for PC1 and PC2 respectively), while the contribution of protein constraints and gene age (PC3) was 24%.

Biological, not technical, noise is responsible for the observed patterns

The noise in gene expression measured from single-cell transcriptomics is a combination of biological and technical noise. While the two sources of noise are a priori independent, gene-specific technical noise has been observed in microarray experiments (Pozhitkov et al. 2007), making a correlation of the two types of noise plausible. If similar effects also affect RNA sequencing experiments, technical noise could be correlated to gene function and therefore act as a covariate in our analyses. To assess whether this is the case, we used the data set of Shalek et al. (2013), which contains both single-cell transcriptomics and three replicates of 10,000 pooled-cell RNA sequencing. In traditional RNA sequencing, which is typically performed on pooled populations of several thousands of cells, biological noise is averaged out so that the resulting measured noise between replicates is essentially the result of technical noise. We computed the mean and variance in expression of each gene across the three populations of cells. By plotting the variance vs. the mean in log-space, we were able to compute a technical F* ($F_t^{\ast }$) value for each gene (see Materials and Methods). We fitted linear models as for the single-cell data using $F_t^{\ast }$instead of F*. We report that no variable had a significant effect on $F_t^{\ast }$(Table S3). In addition, there was no enrichment of the lower 10th $F_t^{\ast }$ percentile for any particular pathway or GO term. The upper 90th percentile showed no GO term enrichment, but four pathways appeared to be significant: “Chromosome maintenance” (adjusted P-value = 0.0043), “Polymerase switching on the C-strand of the telomere” (adjusted P-value = 0.0062), “Polymerase switching” (adjusted P-value = 0.0062), and “Leading strand synthesis” (adjusted P-value = 0.0062), which all relate to DNA replication. While it is unclear why genes involved in these pathways would display higher technical variance in RNA sequencing, these results differ strikingly from our analyses of single-cell RNA sequencing and therefore suggest that technical variance does not act as a confounding factor in our analyses.

Because only three replicates were available in the pooled RNA sequencing data set, we asked whether the resulting estimate of mean and variance in expression is accurate enough to allow proper inference of noise and its correlation with other variables. We conducted a jackknife procedure, where we sampled the original cells from the ESC data set and reestimated F* for each sample. We tested combinations of 3, 5, 10, and 15 cells, with 1000 samples in each case. In each sample, we computed F* with the same procedure as for the complete data set, and fitted a linear model with all 13 synthetic variables. For computational efficiency, we did not include 3D correlation in this analysis. We compute for each variable the number of samples where the effect is significant at the 5% level and has the same sign as in the model fitted on the full data set. We find that the model coefficients are very robust to the number of cells used (Figure S9A) and that three cells are enough to infer the effect of the PC1 and PC3 variables, the most significant in our analyses. Two main conclusions can be drawn from this jackknife analysis: (1) that the lack of significant effect of our explanatory variables on technical noise is not due to the low number of replicates used to compute the mean and variance in expression, and (2) that our conclusions are very robust to the actual cells used in the analysis, ruling out drop-out and amplification biases as possible source of errors (Kharchenko et al. 2014).

Discussion

Through this work, we provide the first genome-wide evolutionary and systemic study of transcriptional noise, using mouse cells as a model. We have shown that transcriptional noise correlates with functional constraints not only at the level of the gene itself via the protein it encodes, but also at the level of the pathway(s) the gene belongs to. We further discuss here potential confounding factors in our analyses and argue that our results are compatible with selection acting to reduce noise propagation at the network level.

In this study, we exhibited several factors explaining the variation in transcriptional noise between genes. While highly significant, the effects we report are of small size, and a complex model accounting for all tested sources of variation only explains a few percent of the total observed variance. There are several possible explanations for this reduced explanatory power. (1) Transcriptional noise is a proxy for noise in gene expression, at which selection occurs (Figure 1). As transcriptional noise is not randomly distributed across the genome, it must constitute a significant component of expression noise, in agreement with previous observations (Blake et al. 2003; Newman et al. 2006). However, translational noise might constitute an important part of the expression noise and was not assessed in this study. (2) Gene expression levels were assessed on ESCs in culture. Such an experimental system may result in gene expression that differs from that in natural conditions under which natural selection acted. (3) Functional annotations in particular pathways and gene interaction are incomplete, and network-based measures most likely have large error rates. (4) While the newly introduced F* measure allowed us to assess the distribution of transcriptional noise independently of the average mean expression, it does not capture the full complexity of SGE. Explicit modeling, for instance based in the β-Poisson model (Vu et al. 2016), is a promising avenue for the development of more sophisticated quantitative measures.

In a pioneering study, Fraser et al. (2004), followed by Shalek et al. (2013), demonstrated that essential genes whose deletion is deleterious, and genes encoding subunits of molecular complexes as well as housekeeping genes, display reduced gene expression noise. Our findings go beyond these early observations by providing a statistical assessment of the joint effect of multiple explanatory factors. Our analyses reveal that network centrality measures are the explanatory factors that explain the most significant part of the distribution of transcriptional noise in the genome. Network-based statistics were first tested by Li et al. (2010) using PPI data in Yeast. While we are able to extend these results to mouse cells, we show that more detailed annotation, as provided by the Reactome database, can lead to new insights into the selective forces acting on expression noise. Our results suggest that pathways constitute a relevant systemic level of organization, at which selection can act and drive the evolution of SGE at the gene level. This multi-level selection mechanism, we propose, can be explained by selection against noise propagation within networks. It has been experimentally demonstrated that expression noise can be transmitted from one gene to another with which it is interacting (Pedraza and van Oudenaarden 2005). Large noise at the network level is deleterious (Barkai and Leibler 1999) but each gene does not contribute equally to it, thus the strength of selective pressure against noise varies among genes in a given network. We have shown that highly connected, “central” proteins typically display reduced transcriptional noise. Such nodes are likely to constitute key players in the flow of noise in intracellular networks as they are more likely to transmit noise to other components. In accordance with this hypothesis, we find genes with the lowest amount of transcriptional noise to be enriched for top-level functions, particularly if they are involved in the regulation of other genes.

These results have several implications for the evolution of gene networks. First, this means that new connections in a network can potentially be deleterious if they link genes with highly stochastic expression. Second, distinct selective pressures at the “regulome” and “interactome” levels (Figure 1) might act in opposite directions. We expect genes encoding highly connected proteins to have more complex regulation schemes, particularly if their proteins are involved in several biological pathways. In accordance, several studies have demonstrated that expression noise of a gene positively correlates with the number of TFs controlling its regulation (Sharon et al. 2014), a correlation that we also find significant in the data set analyzed in this work. Central genes, while being under negative selection against stochastic behavior, are then more likely to be controlled by numerous TFs that increase transcriptional noise. As a consequence, if the number of connections at the interactome level is correlated with the number of connections at the regulome level, we predict the existence of a trade-off in the number of connections that a gene can make in a network. Alternatively, highly connected genes might evolve regulatory mechanisms allowing them to uncouple these two levels: negative feedback loops, for instance, where the product of a gene downregulates its own production, have been shown to stabilize expression and significantly reduce stochasticity (Becskei and Serrano 2000; Dublanche et al. 2006; Tao et al. 2007). We therefore predict that negative feedback loops are more likely to occur at genes that are more central in protein networks, as they will confer greater resilience against high SGE, which is advantageous for this class of genes.

Our results enabled the identification of possible selective pressures acting on the level of stochasticity in gene expression. However, the mechanisms by which the amount of stochasticity can be controlled remain to be elucidated. We evoked the existence of negative feedback loops that reduce stochasticity and the multiplicity of upstream regulators that increase it. Recent work by Wolf et al. (2015) and Metzger et al. (2015) add further perspective to this scheme. Wolf and colleagues found that, in Escherichia coli, noise is higher for natural than experimentally evolved promoters selected for their mean expression level. They hypothesized that higher noise is selectively advantageous in cases of changing environments. On the other hand, Metzger and colleagues performed mutagenesis experiments and found signatures of selection for reduced noise in natural populations of S. cerevisiae. These seemingly opposing results, combined with our observations, provide additional evidence that the amount of stochasticity in the expression of single genes has an optimum, as high values are deleterious because of noise propagation in the network; while lower values, which result in reduced phenotypic plasticity, might be suboptimal in cases of dynamic environments.

Conclusions

Using a new measure of transcriptional noise, our results demonstrate that the position of a protein in the interactome is a major driver of selection against SGE. As such, transcriptional noise is an essential component of the phenotype, in addition to the mean expression level and the actual sequence and structure of the encoded proteins. This is currently an underappreciated phenomenon, and gene expression studies that focus only on the mean expression of genes may be missing key information about expression diversity. The study of gene expression must consider changes in noise in addition to changes in mean expression level as a putative explanation for adaptation. However, further work that aims to unravel the exact structure of the regulome is needed to fully understand how transcriptional noise is generated or inhibited.

Supplementary Material

Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.117.300467/-/DC1.