Abstract
Purpose
To develop a phantom for validating MRI pulse sequences and data processing methods to quantify microscopic diffusion anisotropy in the human brain.
Methods
Using a liquid crystal consisting of water, detergent, and hydrocarbon, we designed a 0.5‐L spherical phantom showing the theoretically highest possible degree of microscopic anisotropy. Data were acquired on the Connectome scanner using echo‐planar imaging signal readout and diffusion encoding with axisymmetric b‐tensors of varying magnitude, anisotropy, and orientation. The mean diffusivity, fractional anisotropy (FA), and microscopic FA (µFA) parameters were estimated.
Results
The phantom was observed to have values of mean diffusivity similar to brain tissue, and relaxation times compatible with echo‐planar imaging echo times on the order of 100 ms. The estimated values of µFA were at the theoretical maximum of 1.0, whereas the values of FA spanned the interval from 0.0 to 0.8 as a result of varying orientational order of the anisotropic domains within each voxel.
Conclusions
The proposed phantom can be manufactured by mixing three widely available chemicals in volumes comparable to a human head. The acquired data are in excellent agreement with theoretical predictions, showing that the phantom is ideal for validating methods for measuring microscopic diffusion anisotropy on clinical MRI systems. Magn Reson Med 79:1817–1828, 2018. © 2017 The Authors Magnetic Resonance in Medicine published by Wiley Periodicals, Inc. on behalf of International Society for Magnetic Resonance in Medicine. This is an open access article under the terms of the Creative Commons Attribution‐NonCommercial License, which permits use, distribution and reproduction in any medium, provided the original work is properly cited and is not used for commercial purposes.
Keywords: dMRI, q‐trajectory, QTE, gamma model, powder averaging, microstructure
INTRODUCTION
Magnetic resonance imaging measurements of the directional dependence of water diffusion 1 offer the possibility of noninvasive investigations of the microstructure of anisotropic biological tissues, e.g., muscle 2, 3, cartilage 4, and brain white matter 5, 6, 7. Diffusion tensor imaging (DTI) 8, 9 relies on diffusion encoding with the Stejskal‐Tanner sequence 10 over multiple directions to estimate maps of diffusion tensors and rotationally invariant scalar parameters, such as the mean diffusivity (MD) and the fractional anisotropy (FA) 11, 12. For brain white matter, these parameters are affected by the microstructural organization of the nerve fibers 13, and therefore allow for inferring micrometer‐scale tissue properties from images with millimeter‐scale spatial resolution. Consequently, DTI and related methods have been applied extensively for studying the microstructure and connectivity of the human brain 14, 15, 16, 17.
Because of the limited spatial resolution of the images, each voxel likely contains multiple tissue types or fiber populations 18, leading to ambiguities when interpreting the DTI parameters in terms of microstructural features 19, 20. As an example, to correctly estimate the distribution of fiber orientations, it is necessary to first quantify the local diffusion characteristics within a single fiber bundle 21, which is influenced by the packing density, diameter, and myelination of the fibers. For locally anisotropic materials that exhibit no diffusion anisotropy on the macroscopic scale because of low orientational order, the microscopic diffusivities within the anisotropic domains can be estimated by detailed analysis of the signal decay as a function of the diffusion weighting variable b, as demonstrated for a wide range of biological and synthetic materials 22, 23, 24, 25, 26, 27, 28, 29, 30. This type of analysis relies on the assumption that all of the anisotropic domains have identical local diffusion properties, and that orientation dispersion is the only mechanism contributing to the observed distribution of effective diffusivities. However, the presence of multiple water compartments with different isotropic diffusivities can give rise to signals that are virtually indistinguishable from the ones originating from compartments with microscopic anisotropy combined with orientation dispersion 31, 32, and the analysis is fraught with ambiguity for materials that are heterogeneous on the voxel scale (brain tissue being a prime example).
Microscopic anisotropy and isotropic heterogeneity can be disambiguated with more advanced diffusion‐encoding schemes that are classified as double diffusion encoding 33, 34, 35, 36, triple diffusion encoding 37, and q‐trajectory encoding 32, 38, 39 following the terminology suggested by Shemesh et al. 40. Within this naming convention, the Stejskal‐Tanner experiment 10 is denoted as single‐diffusion encoding. Lasič et al. 41 showed that the isotropic diffusion encoding 32, 42, 43, 44, 45, 46 incarnation of q‐trajectory encoding is instrumental for separating and quantifying the effects of isotropic heterogeneity, microscopic anisotropy, and orientational order, which are inextricably entangled in conventional diffusion MRI. Because the voxel‐scale anisotropy from DTI is usually reported in terms of the FA parameter, we have defined the microscopic fractional anisotropy (μFA) as a microscopic equivalent that is not affected by orientation dispersion 41, 47. The definition of μFA is identical to the one for the fractional eccentricity of Jespersen et al. 36, 40, 48, but differs from the microscopic anisotropy index of Lawrenz et al. 49. Parameters for quantifying heterogeneity, anisotropy, and orientations are discussed in depth in recent reviews 50, 51, as well as in a series of original research papers 39, 41, 52, 53.
During our last few years of development of NMR and MRI methods for investigating the microstructure of heterogeneous anisotropic tissues, we noticed the need for a standard substance or material to validate pulse sequences, data processing pipelines, and implementations on clinical MRI systems. DTI measurements are typically validated with isotropic liquids 54 and polymer solutions 55, as well as anisotropic physical phantoms made by microcapillaries 56, 57, 58 or wound fibers 59, 60, 61, 62, 63, 64, 65, 66. An ideal phantom for validating microscopic anisotropy measurements should have a well‐defined and uniform value of μFA, a value of MD similar to that observed for brain tissue in vivo, variable degrees of orientational order and values of FA, as well as nuclear relaxation properties allowing for spin‐echo signal preparation and echo‐planar imaging (EPI) readout 67, 68 that is ubiquitous for clinical diffusion MRI sequences. Additionally, the phantom should be inexpensive, stable over long periods of time, and simple to manufacture at sizes comparable to the relevant human anatomy. Previously introduced phantoms were made by randomly oriented microcapillaries 69, chemically fixated pig spinal cord 70, and asparagus puree 41, which all suffer from ill‐defined quantitative values of the microscopic anisotropy. The microcapillary phantom of Komlosh et al. 69 has so far only been used on a vertical bore microimaging system, and the asparagus puree phantom of Lasič et al. 41 is susceptible to odorous biological degradation.
In the field of surface and colloid science, there are numerous studies of diffusion anisotropy in lyotropic liquid crystals, in which self‐assembled detergent aggregates hinder the translational motion of the water 24, 34, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89. For methods development on microimaging systems, we have used several liquid crystalline materials to demonstrate and validate new pulse sequences 32, 37, 41, 52, 53, 90, 91. Most of the previously used materials have severe drawbacks that prevent their use on clinical MRI systems. The nonionic detergents used in 32, 41, and 90 yield lamellar liquid crystals with temperature‐dependent anisotropy and rapid transverse relaxation incompatible with single‐shot EPI. The latter drawback also applies to the detergent sodium dioctyl sulfosuccinate 52, which is also known as Aerosol‐OT, AOT, or docusate sodium, and will be referred to as AOT in the following text.
In 91 and 53, we added the hydrocarbon isooctane to the aqueous AOT system to induce the formation of a reverse hexagonal phase 92 as illustrated in Figure 1. The three components AOT, isooctane, and water spontaneously assemble into an anisotropic structure, where the water is confined in cylindrical channels with diameters of a few nanometers and lengths extending hundreds of micrometers or even millimeters 53. On the approximately 100‐ms observational time scale defined by the duration of the diffusion‐encoding block in the MRI pulse sequence, the translational motion of the water is unhindered in the direction of the channels, leading to one‐dimensional root‐mean‐square displacements of approximately 10 μm. The low solubility of water in isooctane prevents translational motion in the plane perpendicular to the direction of the channels. Consequently, we expect the structure in Figure 1 to give rise to the largest possible microscopic anisotropy and a value of μFA equal to one. In case all anisotropic domains within a voxel have the same orientation, the values of FA and μFA are identical. Unless effort is made to align the domains, each voxel will contain domains of many different orientations, causing FA to be smaller than μFA. A quantitative relation among FA, μFA, and the orientational order parameter is given in 41.
Figure 1.
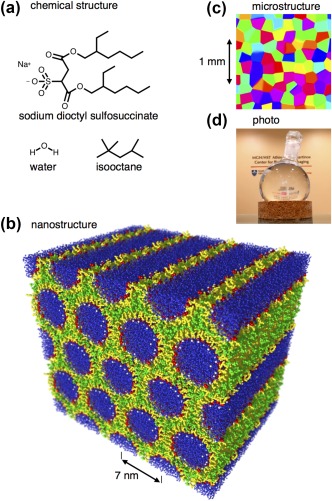
Structure of the liquid crystal phantom. a: Chemical structure of the detergent sodium dioctyl sulfosuccinate, the hydrocarbon isooctane, and water. b: Self‐assembled nanostructure with AOT (white sodium ions, red hydrophilic head groups, yellow hydrophobic tails) in the interface between a continuous matrix of isooctane (green) and hexagonally packed cylindrical rods of water (blue). The structure was generated with the molecular dynamics simulation package GROMACS 122 and rendered with POV‐Ray 123. c: Schematic microstructure with randomly oriented 100‐μm‐scale anisotropic domains color‐coded according to the direction of the six‐fold symmetry axis as [x, y, z] = [red, green, blue]. d: Photo of the phantom comprising the transparent liquid crystal in a 0.5‐L round‐bottom glass flask on a cork stand in front of the wall logo at the reception of the Athinoula A. Martinos Center at Massachusetts General Hospital 97.
The MRI signal from the phantom includes contributions from all 1H‐containing species of the phantom (i.e., AOT, isooctane, and water), which all occur in a liquid state with molecular reorientation on the pico‐ to nanosecond time scale and translational diffusion similar to the values in the corresponding neat liquids. Despite the rapid reorientation and diffusion, the anisotropy of the liquid crystalline structure leads to incomplete averaging of the intramolecular 1H‐1H dipolar couplings 93, 94 and transverse relaxation times (T 2) on the order of milliseconds for AOT and isooctane. The 1H‐1H dipolar couplings of water are also averaged by chemical exchange of hydrogen atoms between neighboring water molecules, giving T 2 values of tens or hundreds of milliseconds. Consequently, we expect only water to contribute to the single‐shot EPI signal.
In this paper, we use experimental methods from surface and colloid science 92, 95 to systematically explore the liquid crystal phase structure for the AOT‐isooctane‐water system as a function of chemical composition, to maximize the water content of the reverse hexagonal phase and increase T 2 to values allowing for single‐shot EPI. Using this chemical composition, we scale up the manufacturing process and construct a phantom with dimensions appropriate to test MRI systems for human brain measurements. We demonstrate the phantom by validating our recent implementation of axisymmetric diffusion‐encoding tensors 52, 96 with smoothly modulated gradient waveforms 53 and EPI signal readout on the Connectome scanner at the Athinoula A. Martinos Center at Massachusetts General Hospital 97, as well as a protocol with numerically optimized waveforms 90, 98 on a conventional scanner. In addition to conventional DTI processing to estimate FA, we analyze the data with the gamma model 41, 99, 100, giving quantitative estimates of the isotropic heterogeneity and the microscopic anisotropy as quantified by μFA 41. Because the gamma model is valid only in the limit of low b‐values, we also analyze the data with the Pake model of Eriksson et al. 52, which is valid for the full range of b‐values in case all anisotropic domains within a voxel have the same local diffusion properties. Although the gamma model is more generally applicable to heterogeneous anisotropic materials such as brain tissue, the Pake model is better suited for verifying that the phantom has the expected reverse hexagonal structure and corresponding one‐dimensional water diffusion. We show that the liquid crystal phantom has ideal properties for thorough testing of new MRI methods to quantify microscopic diffusion anisotropy on clinical MRI systems.
METHODS
Preparation of the Liquid Crystal Phantom
Sodium dioctyl sulfosuccinate (AOT) (purum, ≥ 96%, TLC, lot no. BCBQ6818V) and isooctane (anhydrous, 99.8%, lot no. STBF6788V) were purchased from Sigma‐Aldrich (St. Louis, MO). The water used was purified with a Millipore‐Q water system. Samples for assessment of the phase diagram were prepared from stock solutions of different proportions of AOT and isooctane, which were diluted with water in 4‐mL glass vials to obtain 95 compositions within the region of interest, which was identified based on previously published phase diagrams 92, 95. Note that the stock solutions are viscous and highly flammable liquids 101 that should not be exposed to open flames or electrical discharges. The addition of water to the stock solutions greatly reduces the flammability. All 95 samples were stored and investigated at 25°C, and six that were identified as having the reverse hexagonal structure were further studied as a function of temperature in the range from 5 to 40°C.
The identity and compositional extension of the different phases were determined from characterization of the samples by visual inspection (for general appearance, viscosity, and possible birefringence), polarized light microscopy (for identification of characteristic birefringence patterns of the anisotropic phases), and for selected samples, small‐angle X‐ray scattering (SAXS) for identification of nanostructure. The SAXS experiments were performed on a laboratory SAXS instrument from JJ X‐ray (Hørsholm, Denmark), equipped with a 100XL + microfocus X‐ray tube (Rigaku, the Woodlands, TX) with Cu Kα radiation of wavelength 1.542 Å, and a Pilatus detector (Dectris AG, Baden‐Dättwil, Switzerland). The lattice spacing a of the reverse hexagonal phase in the phantom was calculated from the scattering vector Q 1 of the first Bragg peak using the relation
| (1) |
For preparation of the 0.5‐L phantom, isooctane was added to AOT and set to dissolve overnight. Water was added to the AOT‐isooctane solution, giving a final composition of 44.12 Wt % AOT, 13.94 Wt % isooctane, and 41.94 Wt % water, and the mixture was stirred on a magnetic stirrer at 40°C. The melted liquid crystal was gently poured into a 0.5‐L round‐bottom glass flask, avoiding the formation of air bubbles. The liquid crystal was formed by cooling the phantom from 40 to 20°C over a time period of 5 h.
MRI Measurements
Imaging was performed on the Magnetom 3T Skyra Connectome scanner (Siemens Healthcare, Erlangen, Germany) at the Athinoula A. Martinos Center at Massachusetts General Hospital. The scanner is equipped with a gradient system capable of 0.3 Tm−1 maximum amplitude and 200 Tm−1s−1 slew rate, as well as a 64‐channel receiver head coil array. The phantom was put on a cork stand in the head coil and anchored with soft foam pads. Before MRI measurements, the phantom was left within the bore of the magnet for 30 min, to reach the same temperature as its immediate surroundings (approximately 20°C).
A spin‐echo EPI sequence was adapted to allow user‐defined gradient waveforms to be played out before and after the refocusing pulse as shown in Figure 2. An echo time of 140 ms allowed for diffusion‐encoding waveforms of duration τ = 54.95 ms before and after the 6.9‐ms‐long block of spoiler gradients and the refocusing pulse. Images were acquired in 10 slices (7.5 mm thick) with EPI readout at a matrix size of 70 × 70, field of view of 280 × 280 mm2, and a spatial resolution of 4.0 × 4.0 × 7.5 mm3. The waveforms before and after refocusing were identical and self‐balanced, meaning that the integral of the gradient on each side was zero. Using the explicit equations in the following section, we generated gradient waveforms G(t) at diffusion‐encoding strengths b = 0.25, 0.5, 1, 2, 4, and 8·109 sm−2, normalized anisotropy b Δ = 0, 0.58, 0.82, and 1, along 20 encoding directions. In total, the acquisition generated 480 signal samples per voxel at a repetition time of 2000 ms, giving a total measurement time of 16 min. All data were corrected for motion and eddy currents in elastix 102 using extrapolated reference images 103. Based on the repeated measurements at b Δ = 0, the mean signal‐to‐noise ratio was estimated to 30 at the minimum b‐value of 0.25·109 sm−2.
Figure 2.
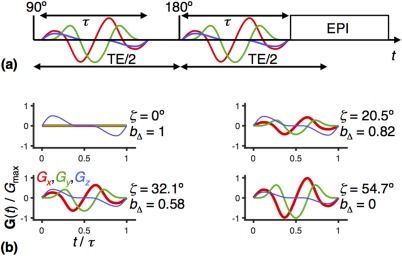
MRI pulse sequence for axisymmetric diffusion encoding 41, 53. a: Spin‐echo sequence with EPI image readout 67, 68 and a pair of modulated gradient waveforms with duration τ (red, green, and blue lines) encoding the signal for translational motion. The 90° and 180° radiofrequency pulses generate a spin echo at the echo time TE. b: Four examples of gradient waveforms G(t) calculated with Equations [2] to [6] for the angles ζ = 0°, 20.5°, 32.1°, and 54.7°. All examples have the same b‐value, whereas the b‐tensor anisotropy b Δ is given by the value of ζ through Equation [7]. The global maximum gradient amplitude for the set of waveforms is G max.
Gradient Waveform Design
We calculated G(t) according to 53 by first specifying an axial waveform G A(t) with total duration τ, quarter‐sine ramp up 0.12τ, and half‐sine ramp down 0.3τ, as shown in Figure 2(b), top left panel. The q‐vector magnitude q(t), trace of the diffusion‐encoding tensor b (also known as the b‐value), azimuthal angle ψ(t), and complex radial waveform G R(t) are given by, respectively,
| (2) |
| (3) |
| (4) |
| (5) |
Subsequently, G(t) is obtained by
| (6) |
in which the polar angle gives b Δ through (52)
| (7) |
In Equation [7], P 2(x) = (3x 2 – 1)/2 is the second Legendre polynomial.
For data evaluation purposes, the full diffusion‐encoding tensor b was calculated with
| (8) |
where
| (9) |
and G(t) is the explicit gradient waveform played out on the scanner, including the effects of rotation and amplitude scaling.
Data Analysis
For each voxel, the diffusion tensor D was estimated by nonlinear fitting of the DTI model 8, 104, 105
| (10) |
to the experimental signal intensities S(b) using seven adjustable parameters, namely the initial signal S 0, the diffusion tensor eigenvalues λ 1, λ 2 and λ 3, and the three Euler angles describing the tensor orientation. The tensor scalar product b:D is defined by
| (11) |
and the tensor elements Dij were evaluated from the eigenvalues and Euler angles using equations given in 106. For voxels containing a distribution of microscopic diffusion tensors, Equation [10] is valid in the limit S(b)/S 0 → 1 39, 50. To minimize systematic errors caused by violating this condition, only data points fulfilling S(b)/S 0 > 0.5 were included in the fitting procedure. After estimating λ 1, λ 2 and λ 3, the values of MD and FA were calculated using 11
| (12) |
and
| (13) |
respectively.
When estimating μFA, the full set of 480 experimental data points S(b, b Δ, θ, ϕ) was “powder‐averaged” over the 20 orientations 41, 50, leaving a reduced set of 6 × 4 points S(b, b Δ). These data were analyzed by assuming a gamma distribution of effective diffusivities P(D), the Laplace transformation of which is given by 41, 50, 100
| (14) |
where V iso and V aniso are the isotropic and anisotropic contributions to the variance of P(D). Equation [14] was regressed onto the experimental data using S 0, MD, V iso, and V aniso as adjustable parameters. In the limit S(b, b Δ)/S 0 → 1, Equation [14] is valid for any distribution P(D). Following 41, only data points fulfilling exp(–bMD) > 0.1 were included in the analysis, to alleviate systematic errors. The estimated values of MD and V aniso were converted to μFA using the expression 41
| (15) |
Values of μFA were also estimated by fitting
| (16) |
to the experimental data using the adjustable parameters S 0, the isotropic diffusivity D iso, and the normalized diffusion tensor anisotropy D Δ 50, 52. Equation [16] is the Laplace transformation of a distribution P(D) corresponding to the powder pattern from an axially symmetric chemical‐shift tensor in solid‐state NMR spectroscopy 107, the functional form of which was originally derived by Pake 108. Unlike Equations [10] and [14], the expression in Equation [16] is valid for any value of S(b, b Δ)/S 0, but only as long as all subensembles of water within the voxel have the same values of D iso and D Δ. Under these conditions, MD = D iso and V iso = 0, and μFA can be calculated from Equation [15] using the substitution 52
| (17) |
For brevity, Equations [10], [14], and [16] will be referred to as the DTI, gamma, and Pake models, respectively. These models are included in the Multidimensional Diffusion MRI software package available at github.com/markus-nilsson/md-dmri.
RESULTS
AOT‐Isooctane‐Water Phase Diagram
Results from the characterization of the AOT‐isooctane‐water samples are presented as a partial ternary phase diagram in Figure 3. Although there are deviations in the extensions of the respective phase regions, the general features are consistent with those of a previously published phase diagram for the same system 95. The observed differences can tentatively be attributed to differences in the qualities of the used chemicals.
Figure 3.
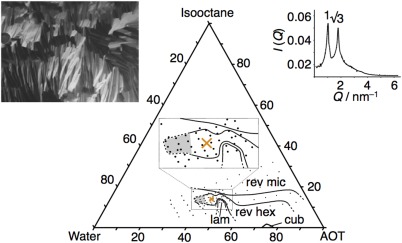
Ternary phase diagram of the AOT‐isooctane‐water system at 25°C. The investigated part of the phase diagram consists of single‐phase regions of lamellar liquid crystalline (LC) phase (lam), cubic LC phase (cub), reverse hexagonal LC phase (rev hex), and reverse micellar solution (rev mic). The main features of the diagram are consistent with the phase diagram of the same system presented in 95. Black dots show the compositions of the samples used in the present investigation, and the orange cross indicates the composition selected for manufacturing of the phantom (44.12 Wt % AOT, 13.94 Wt % isooctane, and 41.94 Wt % water). Samples with compositions within the shaded region were difficult to characterize unambiguously, but inspection in cross‐polarized light revealed that they consist primarily of anisotropic phases (likely involving reverse hexagonal and/or lamellar). The insets display a polarized light microscopy image (left) and a plot of the SAXS intensity I versus the scattering vector Q (right) for a sample with the composition used in the phantom, which both confirm that the sample shows hexagonal nanostructure.
Samples with compositions at and around the value selected for the phantom (orange cross in Fig. 3) show the macroscopically homogeneous appearance of a stiff, optically clear (or slightly hazy) gel that is expected for a hexagonal liquid crystalline phase. Furthermore, investigation of these samples in polarized light microscopy reveals a birefringence pattern characteristic of a hexagonal phase 109, and the relative positions of the reflections in the SAXS profile obey the expected ratio of 1:31/2 110 (see inserts in Fig. 3). Inserting the value of Q 1 for the first SAXS reflection into Equation [1] yields a distance a = 7 nm between the centers of neighboring water cylinders as indicated in Figure 1b.
The stability of the reverse hexagonal phase with respect to temperature is reported in Supporting Table S1. Although the reverse hexagonal structure persists to the lowest investigated temperature of 5°C for all samples, it melts into an isotropic liquid at a temperature that depends on the chemical composition. For the composition chosen for the phantom, melting takes place at 31°C.
Magnetic Resonance Imaging Measurements
Parameter maps and histograms for the liquid crystal phantom are shown in Figure 4 and Supporting Figure S1, and the estimated values of MD, FA, and μFA are compiled in Table 1. Although the DTI, gamma, and Pake models give similar results for the S 0 and MD parameters, the results are (as expected) radically different for FA from DTI and μFA from gamma and Pake. The relations between the appearance of the parameter maps, the assumptions of the various models, and the phantom structure are covered in detail in the “Discussion” section.
Figure 4.
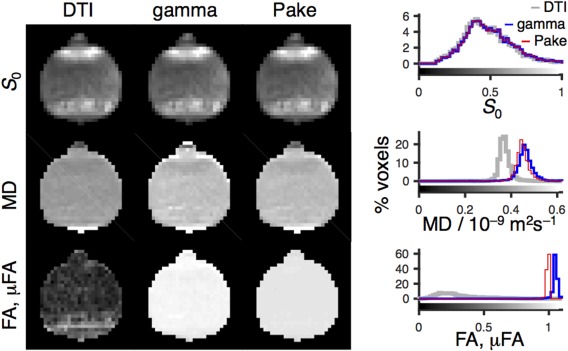
MRI data acquired with the Connectome scanner using the liquid crystal phantom in Figure 1 and the pulse sequence in Figure 2. The data were analyzed with the DTI (column 1), gamma (column 2), and Pake (column 3) models (see Eqs. [10], [14], and [16]), yielding parameter maps of the initial signal intensity S 0 (row 1), the mean diffusivity MD (row 2), as well as the fractional anisotropy FA from DTI and the microscopic fractional anisotropy μFA from the gamma and Pake models (row 3). The 2D parameter maps show the axial slice through the center of the nearly spherical phantom (see Supporting Fig. S1 for all slices). The histograms (right) include data from all 4281 analyzed voxels throughout all slices of the 3D volume. The gray scales of the maps are given by the bars along the abscissas of the histograms. Note that although DTI largely fails to detect anisotropy, both gamma and Pake models yield μFA near the expected value of unity.
Table 1.
Diffusion Parameters (Global Mean ± Standard Deviation) for the Liquid Crystal Phantom.
| MD/10−9 m2s−1 | FA, μFA | |
|---|---|---|
| DTI | 0.37 ± 0.03 | 0.3 ± 0.2 |
| gamma | 0.46 ± 0.04 | 1.05 ± 0.03 |
| Pake | 0.45 ± 0.04 | 0.99 ± 0.01 |
The quality of fit for the gamma and Pake models can be judged from the S(b, b Δ) data shown for four voxels in Figure 5. The root‐mean‐square deviation between data and fit is in the range between 0.01 and 0.02, and the deviation is approximately 40% higher for the gamma model, which is consistent with the small but visually apparent discrepancies between the experimental data and the model fit at the highest b‐value. The voxels are selected to include high and low values of both S 0 and FA. Despite the differences in these parameters, the normalized signals S(b, b Δ)/S 0 are nearly identical for all voxels.
Figure 5.
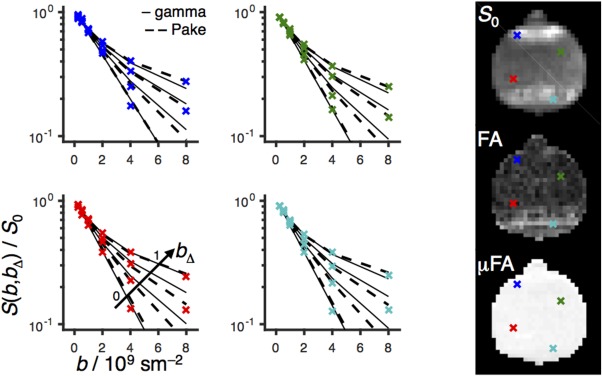
Powder‐averaged normalized signal intensity S(b, b Δ)/S 0 versus b for four voxels indicated as blue, green, red, and turquoise crosses on the S 0, FA, and μFA parameter maps to the right. Experimental S(b, b Δ) data points are shown as crosses; gamma and Pake model fits are represented by solid and dashed lines for each value of the b‐tensor anisotropy b Δ (0, 0.58, 0.82, and 1 from bottom to top as shown with the arrow in the bottom‐left panel).
Additional data showing the reproducibility of the phantom with time and its applicability on a conventional scanner can be found in Supporting Figures S2 and S3.
DISCUSSION
Selecting the Chemical Composition of the Phantom
Spin‐echo sequences with diffusion‐encoding gradients and EPI signal readout require transverse relaxation times (T 2) above approximately 50 ms. Increasing water content leads to larger values of T 2, and to obtain the highest possible value we chose to make the phantom using the composition 44.12 Wt % AOT, 13.94 Wt % isooctane, and 41.94 Wt % water, as indicated with a cross in Figure 3. At this water content, the region of stability of the pure reverse hexagonal phase is narrow with respect to changes in the AOT and isooctane concentrations, and the components have to be weighed with a precision of ±2% to achieve a homogeneous sample with the desired anisotropic structure. At the selected chemical composition, the reverse hexagonal phase was observed to melt into a low‐viscous isotropic liquid at 31 ºC (see Supporting Table S1), and the equilibration, inspection, and analysis of the phantom consequently have to be done below this temperature.
Appearance of the Parameter Maps
Despite the fact that the phantom is perfectly transparent and visually homogeneous, as shown in the photo in Figure 1d, there is a pronounced inhomogeneity in the S 0 maps in Figure 4 on account of differences in T 2 and the dephasing time , which depend on the orientation of the liquid crystalline domains with respect to the main magnetic field, as well as magnetic susceptibility differences between the phantom and the surrounding air. Orientational dependence of T 2 and is a common feature for anisotropic materials such as liquid crystals 22, 111, cartilage 112, 113, and brain tissue 114, 115.
The MD maps in Figure 4 are nearly homogeneous for all models, consistent with the expectedly uniform chemical composition and liquid crystalline phase structure illustrated in Figure 1b. The obtained values of approximately 0.4·10−9 m2s−1 are comparable to MD for white matter, which is typically in the range of 0.8 to 1.0·10−9 m2s−1 20, 116. A few voxels in the very bottom of the phantom display elevated values of MD, which we attribute to artifacts from less‐than‐perfect eddy current correction at high b‐values.
As demonstrated experimentally in 53 and illustrated in Figure 1b, each voxel contains multiple anisotropic domains with nearly random distribution of orientations, giving rise to low anisotropy on the macroscopic scale despite the essentially one‐dimensional water diffusion within each domain. Consequently, the μFA maps from the gamma and Pake model fits are uniform with values near unity, whereas the FA map from the DTI model features a broad range of values between 0 and 0.8, with values of approximately 0.2 being most common. Because the microscopic anisotropy is constant, the FA map reflects the orientational order of the domains within each voxel 41. If desired, the DTI, gamma, and Pake maps can be converted to quantitative maps of the orientational order parameter 41 or the Saupe order tensor 53. Macroscopic alignment of the anisotropic domains can be induced by, for example, the presence of glass surfaces or temperature gradients when forming the liquid crystal from the isotropic liquid 89. The hyperintense band in the FA map toward the bottom of the phantom can be attributed to such voxel‐scale alignment of the anisotropic domains.
Information Gained by Varying the b‐Tensor Anisotropy b Δ
The S(b, b Δ) data sets in Figure 5 are displayed as semilogarithmic graphs of the signal S versus b for the four values of b Δ. The value b Δ = 1 corresponds to directional diffusion encoding as obtained with pulse sequences based on the conventional Stejskal‐Tanner experiment 10, which are ubiquitous in diffusion MRI. The pronounced curvature indicates the presence of multiple water components having different values of the effective diffusivity D, giving rise to a broad distribution of effective diffusivities P(D). Assuming that the distribution originates from an ensemble of randomly oriented axially symmetric domains, the values of the principal diffusivities D || and D ⊥ can be estimated by analyzing the data with expressions corresponding to the b Δ = 1 version of the Pake model in Equation [16]. Despite the widespread use of Pake (b Δ = 1) analysis in the literature 22, 23, 24, 25, 26, 27, 28, 29, 30, it is not appropriate for complex materials such as biological tissues, as multiple microscopic structures, which are not necessarily anisotropic, can give rise to exactly the same distribution P(D) and signal S(b) 31, 41.
Microscopic anisotropy as the underlying cause of the curvature of logS‐vs‐b can be proven by applying isotropic diffusion encoding, corresponding to b Δ = 0 32. In case of anisotropy as the sole mechanism contributing to the curvature, a monoexponential decay is obtained when b Δ = 0 32. Such behavior is indeed observed in Figure 5. In contrast, if the curvature was caused by isotropic mechanisms, then there would be no difference between the b Δ = 0 and 1 data 32. As shown in Figure 5, the Pake model fits well to the experimental data for all values of b Δ from the marked multiexponentiality at b Δ = 1 to the monoexponential decay at b Δ = 0, as expected for signal that originates from a single water component with unique values of D iso and D Δ or, equivalently, D || and D ⊥. The excellent agreement between the experimental data and the Pake model, as well as the near‐ideal values μFA = 0.99 ± 0.01, verifies that the liquid crystal phantom has the appropriate properties for validating MRI methods for quantifying microscopic anisotropy.
Parameter Bias Resulting From the Model Assumptions
For voxels containing several domain orientations and corresponding diffusion tensors, the DTI model is only valid in the limit S(b)/S 0 → 1 51. Model fitting using data points outside the range of validity causes systematic underestimation of MD. Even the rather narrow range S(b)/S 0 > 0.5 used here gives rise to a –20% bias in the values of MD for the DTI model in comparison to the gamma and Pake models, as shown in the MD histograms in Figure 4.
Although the μFA maps from the gamma and Pake fits appear similar, closer scrutiny of the corresponding histograms in Figure 4 reveals that the gamma and Pake models give values of, respectively, 1.05 ± 0.03 and 0.99 ± 0.01 (global mean ± standard deviation). The gamma model is valid in the limit S/S 0 → 1 and, as suggested in 41, the model‐fitting procedure only included data points fulfilling the condition exp(–bMD) > 0.1. Despite this restriction of the range of used b‐values, the estimated parameters suffer from a small bias, giving rise to μFA values exceeding the theoretical maximum of unity. Raising the threshold from the current value of 0.1 would reduce the bias, although at the expense of increasing the sensitivity to experimental noise.
Implications for Studies of Heterogeneous Tissues
Although the gamma model suffers from systematic errors, it is superior to the Pake model for heterogeneous materials with multiple values of D iso and D Δ within each voxel. The variance of isotropic diffusivities is captured in the parameter V iso of Equation [14], which has been shown to be nonzero in heterogeneous materials such as a yeast suspension with distinct differences in effective diffusivities of the intra‐ and extracellular water 41, brain parenchyma containing multiple tissue types 20, white matter with elevated levels of “free” water because of neuroinflammation or atrophy 39, and brain tumors with variable cell density 117. More detailed characterization of heterogeneous materials was recently demonstrated with exhaustive sampling of the (b, b Δ) acquisition space on microimaging equipment and data analysis with a multicomponent Pake model that yields the microscopic anisotropy for each component having a distinct value of D iso 51, 91. Two‐ or three‐component analysis has also been applied to human brain data acquired with b Δ = 0 and 1, but has so far relied on narrow constraints on the allowed values of the component diffusivities to reduce the influence of experimental noise and the limited sampling of the (b, b Δ) space 118. We anticipate that data acquired with the protocol used here, having multiple values of b Δ, will allow for relaxing the constraints of the multicomponent data inversion, potentially giving information about heterogeneous tissues at an unprecedented level of detail.
Limitations of the Phantom
The experimental data in Figures 4 and 5 demonstrate that the phantom has the desired properties regarding the values of MD, FA, and μFA. However, there are important precautions that must be taken during preparation, storage, and use of the phantom. The position and extension of the reverse hexagonal phase formed by AOT, isooctane, and water may be influenced by the presence of impurities in the used chemicals. Thus, the composition for obtaining a phantom with optimal properties can vary with the quality and purity of the used chemicals. Because the composition range for formation of a reverse hexagonal phase with high water content is rather narrow (see Fig. 3), it is preferable to prepare a small series of samples with compositions in the vicinity of the expected one, to verify homogeneity, before the phantom is produced.
At the chemical composition used for the scaled‐up phantom, the liquid crystal melts into an isotropic phase at 31°C, which puts an upper limit of the temperature in the scanner room. Because of the limited range of compositions in which the reverse hexagonal phase is thermodynamically stable, it is important to avoid evaporation of water or isooctane that would lead to changes in composition and nanostructure. Although glass is impermeable to both water and isooctane, plastic containers may be permeable to isooctane 119 and therefore ill‐suited for prolonged storage. Vigorous shaking of the phantom will not affect the nanostructure, but could change the size and alignment of the anisotropic domains 120, as well as introduce air bubbles that give artifacts in images obtained with EPI readout. If such bubbles have accidentally been formed, a simple remedy is to heat the phantom to above 31°C, where the liquid crystal melts into a low‐viscous isotropic solution, and let the bubbles disappear through the action of the buoyancy force before cooling down to room temperature. The heating‐cooling procedure could also be applied to “reset” the phantom in case the anisotropic domains have been macroscopically oriented by, for example, extended exposure to the aligning effect of the MRI magnet 121.
CONCLUSIONS
We have shown that a mixture of the detergent AOT, hydrocarbon isooctane, and water, which are all commercially available, inexpensive, and reasonably harmless substances, form a thermodynamically stable liquid crystal with diffusion properties suitable for testing MRI methods to quantify microscopic diffusion anisotropy: MD comparable to that of brain tissue, arbitrary values of FA, and μFA equal to the theoretical maximum of unity. The mixture can conveniently be prepared in large volumes, melted into an isotropic liquid with low viscosity by mild heating, poured into a container with dimensions compatible with the chosen MRI system, and cooled to room temperature to reform the anisotropic liquid crystalline structure. The utility of the phantom was demonstrated by validating our recent implementation of smoothly modulated gradient waveforms 53 for q‐trajectory diffusion encoding 32, 38, 39 on the Connectome scanner 97, giving excellent agreement between the experimental data and the Pake model 52. The acquisition space of b‐tensor magnitudes and anisotropies used in this work corresponds to those required for unconstrained estimation of diffusion tensor distributions using the multidimensional approach introduced in 91 and generalized in 51, thereby paving the way for in vivo mapping of, for example, fiber bundle orientation distributions and “free” water fractions, without relying on poorly motivated constraints or priors.
Supporting information
Fig. S1. Parameter maps for all slices of the experimental data in Figure 4. The S 0, MD, and μFA maps were obtained with the gamma model, whereas the FA map is from standard DTI analysis. The gray scales have the same meanings as in Figure 4.
Fig. S2. Demonstration of the long‐time stability of the phantom. The data were acquired one year after the original measurements reported in Figure 4 and Supporting Figure S1 using the same scanner, experimental settings, and data‐processing pipeline. The phantom was stored at temperatures in the range from 19 to 24°C. The gray scales have the same meanings as in Figure 4. Note that the μFA maps remain uniform with values near unity.
Fig. S3. Application of the phantom on a conventional MR scanner. The data were acquired with the same phantom in Supporting Figure S2 using a conventional Siemens Magnetom Prisma 3T scanner with 0.080 Tm−1 maximum gradient strength and 200 Tm−1s−1 slew rate at a spatial resolution of 2.0 × 2.0 × 4.0 mm3 using an optimized acquisition protocol as described in 98. The data processing pipeline and visualization were the same as in Supporting Figure S1. Note the uniformity of the μFA maps with values near unity.
Table S1. Temperature Stability Range of the Reverse Hexagonal Phase for Samples With Chemical Compositions at and Around the Value Chosen for the Phantom.
ACKNOWLEDGMENTS
Marc Obiols‐Rabasa (CR Competence AB, Lund, Sweden) is gratefully acknowledged for performing the SAXS measurements. The diffusion‐encoding sequence was implemented in the pulse‐programming environment provided by Siemens Healthcare, Erlangen, Germany.
Grant Support: CR Development AB (CR Award MN15), the Swedish Foundation for Strategic Research (AM13‐0090), the Swedish Research Council (2014‐3910, 2016‐04482), and NIH (R01MH074794, P41EB015902, P41EB015898).
M.N., K.B., and D.T. are co‐owners of CR Development AB (Lund, Sweden, http://www.crdev.se/), holding patents related to the described methods.
REFERENCES
- 1. Boss BD, Stejskal EO. Anisotropic diffusion in hydrated vermiculite. J Chem Phys 1965;43:1068–1069. [Google Scholar]
- 2. Tanner JE. Self diffusion of water in frog muscle. Biophys J 1979;28:107–116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Scollan DF, Holmes A, Winslow R, Forder J. Histological validation of myocardial microstructure obtained from diffusion tensor magnetic resonance imaging. Am J Physiol 1998;275:H2308–H2318. [DOI] [PubMed] [Google Scholar]
- 4. Filidoro L, Dietrich O, Weber J, Rauch E, Oerther T, Wick M, Reiser MF, Glaser C. High‐resolution diffusion tensor imaging of human patellar cartilage: feasibility and preliminary findings. Magn Reson Med 2005;53:993–998. [DOI] [PubMed] [Google Scholar]
- 5. Chenevert TL, Brunberg JA, Pipes JG. Anisotropic diffusion in human white matter. Radiology 1990;177:401–405. [DOI] [PubMed] [Google Scholar]
- 6. Moseley ME, Cohen Y, Kucharczyk J, Mintorovitch J, Asgari HS, Wendland MF, Tsuruda J, Norman D. Diffusion‐weighted MR imaging of anisotropic water diffusion in cat central nervous system. Radiology 1990;176:439–445. [DOI] [PubMed] [Google Scholar]
- 7. Moseley ME, Kucharczyk J, Asgari HS, Norman D. Anisotropy in diffusion‐weighted MRI. Magn Reson Med 1991;19:321–326. [DOI] [PubMed] [Google Scholar]
- 8. Basser PJ, Mattiello J, Le Bihan D. MR diffusion tensor spectroscopy and imaging. Biophys J 1994;66:259–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Basser PJ, Jones DK. Diffusion‐tensor MRI: theory, experimental design and data analysis—a technical review. NMR Biomed 2002;15:456–467. [DOI] [PubMed] [Google Scholar]
- 10. Stejskal EO, Tanner JE. Spin diffusion measurements: spin echoes in the presence of a time‐dependent field gradient. J Chem Phys 1965;42:288–292. [Google Scholar]
- 11. Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative‐diffusion‐tensor MRI. J Magn Reson B 1996;111:209–219. [DOI] [PubMed] [Google Scholar]
- 12. Kingsley PB. Introduction to diffusion tensor imaging mathematics. Part II: Anisotropy, diffusion‐weighting factors, and gradient encoding schemes. Conc Magn Reson A 2006;28A:123–154. [Google Scholar]
- 13. Beaulieu C. The basis of anisotropic water diffusion in the nervous system—a technical review. NMR Biomed 2002;15:435–455. [DOI] [PubMed] [Google Scholar]
- 14. Le Bihan D. Looking into the functional architecture of the brain with diffusion MRI. Nat Rev Neurosci 2003;4:469–480. [DOI] [PubMed] [Google Scholar]
- 15. Mori S, van Zijl PCM. Fiber tracking: principles and strategies—a technical review. NMR Biomed 2002;15:468–480. [DOI] [PubMed] [Google Scholar]
- 16. Alexander AL, Lee JE, Lazar M, Field AS. Diffusion tensor imaging of the brain. Neurotherapeutics 2007;4:316–329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Tournier JD, Mori S, Leemans A. Diffusion tensor imaging and beyond. Magn Reson Med 2011;65:1532–1556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Jeurissen B, Leemans A, Tournier JD, Jones DK, Sijbers J. Investigating the prevalence of complex fiber configurations in white matter tissue with diffusion magnetic resonance imaging. Hum Brain Mapp 2013;34:2747–2766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Jones DK, Knosche TR, Turner R. White matter integrity, fiber count, and other fallacies: the do's and don'ts of diffusion MRI. NeuroImage 2013;73:239–254. [DOI] [PubMed] [Google Scholar]
- 20. Szczepankiewicz F, Lasič S, van Westen D, Sundgren PC, Englund E, Westin C‐F, Ståhlberg F, Lätt J, Topgaard D, Nilsson M. Quantification of microscopic diffusion anisotropy disentangles effects of orientation dispersion from microstructure: applications in healthy volunteers and in brain tumors. NeuroImage 2015;104:241–252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Tax CM, Jeurissen B, Vos SB, Viergever MA, Leemans A. Recursive calibration of the fiber response function for spherical deconvolution of diffusion MRI data. NeuroImage 2014;86:67–80. [DOI] [PubMed] [Google Scholar]
- 22. Lindblom G, Wennerström H, Arvidson G. Translational diffusion in model membranes studied by nuclear magnetic resonance. Int J Quantum Chem 1977;XII, Suppl. 2:153–158. [Google Scholar]
- 23. Callaghan PT, Jolley KW, Lelievre J. Diffusion of water in the endosperm tissue of wheat grains as studied by pulsed field gradient nuclear magnetic resonance. Biophys J 1979;28:133–141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Callaghan PT, Söderman O. Examination of the lamellar phase of aerosol OT/water using pulsed field gradient nuclear magnetic resonance. J Phys Chem 1983;87:1737–1744. [Google Scholar]
- 25. Packer KJ, Zelaya FO. Observation of diffusion of fluids in porous solids by pulsed field gradient NMR. Colloids Surf 1989;36:221–227. [Google Scholar]
- 26. Joabsson F, Nydén M, Linse P, Söderman O. Pulsed field gradient NMR studies of translational diffusion in cylindrical surfactant aggregates. J Phys Chem B 1997;101:9710–9716. [Google Scholar]
- 27. Rittig F, Fleischer G, Kärger J, Papadakis M, Almdal K, Stepanek P. Anisotropic self‐diffusion in a hexagonally orderd asymmetric PEP‐PDMS diblock copolymer studied by pulsed field gradient NMR. Macromolecules 1999;32:5872–5877. [Google Scholar]
- 28. Stallmach F, Kärger J, Krause C, Jeschke M, Oberhagemann U. Evidence of anisotropic self‐diffusion of guest molecules in nanoporous materials of MCM‐41 type. J Am Chem Soc 2000;122:9237–9242. [Google Scholar]
- 29. Yablonskiy DA, Sukstanskii AL, Leawoods JC, Gierada DS, Bretthorst GL, Lefrak SS, Cooper JD, Conradi MS. Quantitative in vivo assessment of lung microstructure at the alveolar level with hyperpolarized 3He diffusion MRI. Proc Natl Acad Sci USA 2002;99:3111–3116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Topgaard D, Söderman O. Self‐diffusion in two‐ and three‐dimensional powders of anisotropic domains: an NMR study of the diffusion of water in cellulose and starch. J Phys Chem B 2002;106:11887–11892. [Google Scholar]
- 31. Mitra PP. Multiple wave‐vector extension of the NMR pulsed‐field‐gradient spin‐echo diffusion measurement. Phys Rev B 1995;51:15074–15078. [DOI] [PubMed] [Google Scholar]
- 32. Eriksson S, Lasič S, Topgaard D. Isotropic diffusion weighting by magic‐angle spinning of the q‐vector in PGSE NMR. J Magn Reson 2013;226:13–18. [DOI] [PubMed] [Google Scholar]
- 33. Cory DG, Garroway AN, Miller JB. Applications of spin transport as a probe of local geometry. Polymer Prepr 1990;31:149–150. [Google Scholar]
- 34. Callaghan PT, Furó I. Diffusion‐diffusion correlation and exchange as a signature for local order and dynamics. J Chem Phys 2004;120:4032–4038. [DOI] [PubMed] [Google Scholar]
- 35. Finsterbusch J. Extension of the double‐wave‐vector diffusion‐weighting experiment to multiple concatenations. J Magn Reson 2009;198:174–182. [DOI] [PubMed] [Google Scholar]
- 36. Jespersen SN, Lundell H, Sønderby CK, Dyrby TB. Orientationally invariant metrics of apparent compartment eccentricity from double pulsed field gradient diffusion experiments. NMR Biomed 2013;26:1647–1662. [DOI] [PubMed] [Google Scholar]
- 37. Topgaard D. Isotropic diffusion weighting using a triple‐stimulated echo pulse sequence with bipolar gradient pulse pairs. Microporous Mesoporous Mater 2015;205:48–51. [Google Scholar]
- 38. Topgaard D. Isotropic diffusion weighting in PGSE NMR: numerical optimization of the q‐MAS PGSE sequence. Microporous Mesoporous Mater 2013;178:60–63. [Google Scholar]
- 39. Westin C‐F, Knutsson H, Pasternak O, et al. Q‐space trajectory imaging for multidimensional diffusion MRI of the human brain. NeuroImage 2016;135:345–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Shemesh N, Jespersen SN, Alexander DC, et al. Conventions and nomenclature for double diffusion encoding (DDE) NMR and MRI. Magn Reson Med 2016;75:82–87. [DOI] [PubMed] [Google Scholar]
- 41. Lasič S, Szczepankiewicz F, Eriksson S, Nilsson M, Topgaard D. Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic‐angle spinning of the q‐vector. Front Physics 2014;2:11. [Google Scholar]
- 42. Mori S, van Zijl PCM. Diffusion weighting by the trace of the diffusion tensor within a single scan. Magn Reson Med 1995;33:41–52. [DOI] [PubMed] [Google Scholar]
- 43. Wong EC, Cox RW, Song AW. Optimized isotropic diffusion weighting. Magn Reson Med 1995;34:139–143. [DOI] [PubMed] [Google Scholar]
- 44. de Graaf RA, Braun KPJ, Nicolay K. Single‐shot diffusion trace 1H NMR spectroscopy. Magn Reson Med 2001;45:741–748. [DOI] [PubMed] [Google Scholar]
- 45. Moffat BA, Hall DE, Stojanovska J, McConville PJ, Moody JB, Chenevert TL, Rehemtulla A, Ross BD. Diffusion imaging for evaluation of tumor therapies in preclinical animal models. MAGMA 2004;17:249–259. [DOI] [PubMed] [Google Scholar]
- 46. Valette J, Giraudeau C, Marchadour C, Djemai B, Geffroy F, Ghaly MA, Le Bihan D, Hantraye P, Lebon V, Lethimonnier F. A new sequence for single‐shot diffusion‐weighted NMR spectroscopy by the trace of the diffusion tensor. Magn Reson Med 2012;68:1705–1712. [DOI] [PubMed] [Google Scholar]
- 47. Topgaard D, Lasič S, Nilsson M. Analysis for quantifying microscopic diffusion anisotropy. WIPO PCT/SE2013/050493. 7 November 2013. 1250453‐6 4 May 2012 SE, 61/642,589 4 May 2012. US.
- 48. Jespersen SN, Lundell H, Sønderby CK, Dyrby TB. Commentary on ‘Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientation of order parameter by diffusion MRI with magic‐angle spinning of the q‐vector’. Front Physics 2014;2:28. [Google Scholar]
- 49. Lawrenz M, Koch MA, Finsterbusch J. A tensor model and measures of microscopic anisotropy for double‐wave‐vector diffusion‐weighting experiments with long mixing times. J Magn Reson 2010;202:43–56. [DOI] [PubMed] [Google Scholar]
- 50. Topgaard D. NMR methods for studying microscopic diffusion anisotropy In: Valiullin R, editor. Diffusion NMR of confined systems: fluid transport in porous solids and heterogeneous materials, new developments in NMR. Cambridge, UK: Royal Society of Chemistry; 2016. pp 226–259. [Google Scholar]
- 51. Topgaard D. Multidimensional diffusion MRI. J Magn Reson 2017;275:98–113. [DOI] [PubMed] [Google Scholar]
- 52. Eriksson S, Lasič S, Nilsson M, Westin C‐F, Topgaard D. NMR diffusion encoding with axial symmetry and variable anisotropy: distinguishing between prolate and oblate microscopic diffusion tensors with unknown orientation distribution. J Chem Phys 2015;142:104201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Topgaard D. Director orientations in lyotropic liquid crystals: diffusion MRI mapping of the Saupe order tensor. Phys Chem Chem Phys 2016;18:8545–8553. [DOI] [PubMed] [Google Scholar]
- 54. Malyarenko D, Galban CJ, Londy FJ, Meyer CR, Johnson TD, Rehemtulla A, Ross BD, Chenevert TL. Multi‐system repeatability and reproducibility of apparent diffusion coefficient measurement using an ice‐water phantom. J Magn Reson Imaging 2013;37:1238–1246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Gatidis S, Schmidt H, Martirosian P, Schwenzer NF. Development of an MRI phantom for diffusion‐weighted imaging with independent adjustment of apparent diffusion coefficient values and T 2 relaxation times. Magn Reson Med 2014;72:459–463. [DOI] [PubMed] [Google Scholar]
- 56. von dem Hagen EA, Henkelman RM. Orientational diffusion reflects fiber structure within a voxel. Magn Reson Med 2002;48:454–459. [DOI] [PubMed] [Google Scholar]
- 57. Lin C‐P, Wedeen VJ, Chen J‐H, Yao C, Tseng W‐YI. Validation of diffusion spectrum magnetic resonance imaging with manganese‐enhanced rat optic tracts and ex vivo phantoms. NeuroImage 2003;19:482–495. [DOI] [PubMed] [Google Scholar]
- 58. Yanasak N, Allison J. Use of capillaries in the construction of an MRI phantom for the assessment of diffusion tensor imaging: demonstration of performance. Magn Reson Imaging 2006;24:1349–1361. [DOI] [PubMed] [Google Scholar]
- 59. Perrin M, Poupon C, Rieul B, Leroux P, Constantinesco A, Mangin JF, Le Bihan D. Validation of q‐ball imaging with a diffusion fibre‐crossing phantom on a clinical scanner. Phil Trans R Soc B 2005;360:881–891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Watanabe M, Aoki S, Masutani Y, Abe O, Hayashi N, Masumoto T, Mori H, Kabasawa H, Ohtomo K. Flexible ex vivo phantoms for validation of diffusion tensor tractography on a clinical scanner. Radiat Med 2006;24:605–609. [DOI] [PubMed] [Google Scholar]
- 61. Fieremans E, De Deene Y, Delputte S, Özdemir MS, D'Asseler Y, Vlassenbroeck J, Deblaere K, Achten E, Lemahieu I. Simulation and experimental verification of the diffusion in an anisotropic fiber phantom. J Magn Reson 2008;190:189–199. [DOI] [PubMed] [Google Scholar]
- 62. Poupon C, Rieul B, Kezele I, Perrin M, Poupon F, Mangin JF. New diffusion phantoms dedicated to the study and validation of high‐angular‐resolution diffusion imaging (HARDI) models. Magn Reson Med 2008;60:1276–1283. [DOI] [PubMed] [Google Scholar]
- 63. Lorenz R, Bellemann ME, Hennig J, Il'yasov KA. Anisotropic phantoms for quantitative diffusion tensor imaging and fiber‐tracking validation. Appl Magn Reson 2008;33:419–429. [Google Scholar]
- 64. Farrher E, Kaffanke J, Celik AA, Stöcker T, Grinberg F, Shah NJ. Novel multisection design of anisotropic diffusion phantoms. Magn Reson Imaging 2012;30:518–526. [DOI] [PubMed] [Google Scholar]
- 65. Bach M, Fritzsche KH, Stieltjes B, Laun FB. Investigation of resolution effects using a specialized diffusion tensor phantom. Magn Reson Med 2014;71:1108–1116. [DOI] [PubMed] [Google Scholar]
- 66. Hubbard PL, Zhou FL, Eichhorn SJ, Parker GJ. Biomimetic phantom for the validation of diffusion magnetic resonance imaging. Magn Reson Med 2015;73:299–305. [DOI] [PubMed] [Google Scholar]
- 67. Mansfield P. Multi‐planar image formation using NMR spin echoes. J Phys C 1977;10:L55–L58. [Google Scholar]
- 68. Mansfield P, Pykett IL. Biological and medical imaging by NMR. J Magn Reson 1978;29:355–373. [DOI] [PubMed] [Google Scholar]
- 69. Komlosh ME, Horkay F, Freidlin RZ, Nevo U, Assaf Y, Basser PJ. Detection of microscopic anisotropy in gray matter and in novel tissue phantom using double pulsed gradient spin echo MR. J Magn Reson 2007;189:38–45. [DOI] [PubMed] [Google Scholar]
- 70. Lawrenz M, Finsterbusch J. Detection of microscopic diffusion anisotropy on a whole‐body MR system with double wave vector imaging. Magn Reson Med 2011;66:1405–1415. [DOI] [PubMed] [Google Scholar]
- 71. Tiddy GJT. Magnetic resonance studies of liquid crystal phase structure and self‐diffusion coefficients in the system lithium perfluoro‐octanoate+water. J Chem Soc, Faraday Trans 1 1977;73:1731–1737. [Google Scholar]
- 72. Callaghan PT, Le Gros MA, Pinder DN. The measurement of diffusion using deuterium pulsed field gradient nuclear magnetic resonance. J Chem Phys 1983;79:6372–6381. [Google Scholar]
- 73. Chidichimo G, Coppola L, La Mesa C, Ranieri GA, Saupe A. Structure of the lamellar lyo‐mesophase in water/ammonium perfluorononanoate mixtures: PFG NMR and 2H‐NMR investigations. Chem Phys Lett 1988;145:85–89. [Google Scholar]
- 74. Chung J, Prestegard JH. Characterization of field‐ordered aqueous liquid crystals by NMR diffusion measurements. J Phys Chem 1993;97:9837–9843. [Google Scholar]
- 75. Holmes MC, Sotta P, Hendrikx Y, Deloche B. Water self diffusion in caesium pentadecafluorooctanoate (CsPFO)/H2O and CsPFO/CsCl/H2O and its relationship to structure. J Phys II France 1993;3:1735–1746. [Google Scholar]
- 76. Wassall SR. Pulsed field gradient‐spin echo NMR studies of water diffusion in a phospholipid model membrane. Biophys J 1996;71:2724–2732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Jóhanneson H, Halle B. Solvent diffusion in ordered macrofluids: a stochastic simulation study of the obstruction effect. J Chem Phys 1996;104:6807–6817. [Google Scholar]
- 78. Gaemers S, Bax A. Morphology of three lyotropic liquid crystalline biological NMR media studied by translational diffusion anisotropy. J Am Chem Soc 2001;123:12343–12352. [DOI] [PubMed] [Google Scholar]
- 79. Furó I, Dvinskikh SV. NMR methods applied to anisotropic diffusion. Magn Reson Chem 2002;40:S3–S14. [Google Scholar]
- 80. Callaghan PT, Komlosh ME. Locally anisotropic motion in a macroscopically isotropic system: displacement correlations measured using double pulsed gradient spin‐echo NMR. Magn Reson Chem 2002;40:S15–S19. [Google Scholar]
- 81. Hubbard PL, McGrath KM, Callaghan PT. A study of anisotropic water self‐diffusion and defects in the lamellar mesophase. Langmuir 2005;21:4340–4346. [DOI] [PubMed] [Google Scholar]
- 82. Hubbard PL, McGrath KM, Callaghan PT. Orientational anisotropy in polydomain lamellar phase of a lyotropic liquid crystal. Langmuir 2006;22:3999–4003. [DOI] [PubMed] [Google Scholar]
- 83. Hubbard PL, McGrath KM, Callaghan PT. Evolution of a lamellar domain structure for an equilibrating lyotropic liquid crystal. J Phys Chem B 2006;110:20781–20788. [DOI] [PubMed] [Google Scholar]
- 84. Åslund I, Cabaleiro‐Lago C, Söderman O, Topgaard D. Diffusion NMR for determining the homogeneous length scale in lamellar phases. J Phys Chem B 2008;112:2782–2794. [DOI] [PubMed] [Google Scholar]
- 85. Szutkowski K, Jurga S. Long‐range ordering in the lyotropic lamellar phase studied by high‐resolution magnetic resonance diffusion‐weighted imaging. J Phys Chem B 2010;114:165–173. [DOI] [PubMed] [Google Scholar]
- 86. Åslund I, Medronho B, Topgaard D, Söderman O, Schmidt C. Homogeneous length scale of shear‐induced multilamellar vesicles. J Magn Reson 2011;209:291–299. [DOI] [PubMed] [Google Scholar]
- 87. Medronho B, Brown J, Miguel MG, Schmidt C, Olsson U, Galvosas P. Planar lamellae and onions: a spatially resolved rheo–NMR approach to the shear‐induced structural transformations in a surfactant model system. Soft Matter 2011;7:4938–4947. [Google Scholar]
- 88. Medronho B, Olsson U, Schmidt C, Galvosas P. Transient and steady‐state shear banding in a lamellar phase as studied by rheo‐NMR. Z Phys Chem 2012;226:1293–1314. [Google Scholar]
- 89. Bernin D, Koch V, Nydén M, Topgaard D. Multi‐scale characterization of lyotropic liquid crystals using 2H and diffusion MRI with spatial resolution in three dimensions. PLoS One 2014;9:e98752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90. Sjölund J, Szczepankiewicz F, Nilsson M, Topgaard D, Westin C‐F, Knutsson H. Constrained optimization of gradient waveforms for generalized diffusion encoding. J Magn Reson 2015;261:157–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91. de Almeida Martins JP, Topgaard D. Two‐dimensional correlation of isotropic and directional diffusion using NMR. Phys Rev Lett 2016;116:087601. [DOI] [PubMed] [Google Scholar]
- 92. Jönsson B, Lindman B, Holmberg K, Kronberg B. Surfactants and polymers in aqueous solution. Chichester, UK: John Wiley & Sons; Ltd; 1998. [Google Scholar]
- 93. Wennerström H. Proton nuclear magnetic resonance lineshapes in lamellar liquid crystals. Chem Phys Lett 1973;18:41–44. [Google Scholar]
- 94. Ulmius J, Wennerström H, Lindblom G, Arvidson G. Proton NMR bandshape studies of lamellar liquid crystals and gel phases containing lecithins and cholesterol. Biochim Biophys Acta 1975;389:197–202. [DOI] [PubMed] [Google Scholar]
- 95. Evans DF, Wennerström H. The colloidal domain: where physics, chemistry, biology, and technology meet. New York: Wiley‐VCH; 1999. [Google Scholar]
- 96. Westin C‐F, Szczepankiewicz F, Pasternak O, Özarslan E, Topgaard D, Knutsson H, Nilsson M. Measurement tensors in diffusion MRI: generalizing the concept of diffusion encoding. Med Image Comput Comput Assist Interv 2014;17:209–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97. Setsompop K, Kimmlingen R, Eberlein E, et al. Pushing the limits of in vivo diffusion MRI for the Human Connectome Project. NeuroImage 2013;80:220–233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98. Szczepankiewicz F, Sjölund J, Ståhlberg F, Lätt J, Nilsson M. Whole‐brain diffusional variance decomposition (DIVIDE): demonstration of technical feasibility at clinical MRI systems. arXiv:161206741 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99. Jensen JH, Helpern JA. MRI quantification of non‐Gaussian water diffusion by kurtosis analysis. NMR Biomed 2010;23:698–710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100. Röding M, Bernin D, Jonasson J, Särkkä A, Topgaard D, Rudemo M, Nydén M. The gamma distribution model for pulsed‐field gradient NMR studies of molecular‐weight distributions of polymers. J Magn Reson 2012;222:105–111. [DOI] [PubMed] [Google Scholar]
- 101. Fieser LF, Harris GC, Hershberg EB, Morgana M, Novello FC, Putnam ST. Napalm. Ind Eng Chem 1946;38:768–773. [Google Scholar]
- 102. Klein S, Staring M, Murphy K, Viergever MA, Pluim JP. Elastix: a toolbox for intensity‐based medical image registration. IEEE Trans Med Imaging 2010;29:196–205. [DOI] [PubMed] [Google Scholar]
- 103. Nilsson M, Szczepankiewicz F, van Westen D, Hansson O. Extrapolation‐based references improve motion and eddy‐current correction of high b‐value DWI data: application in Parkinson's disease dementia. PLoS One 2015;10:e0141825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104. Price WS. NMR studies of translational motion. Cambridge, UK: Cambridge University Press; 2009. [Google Scholar]
- 105. Callaghan PT. Translational dynamics & magnetic resonance. Oxford, UK: Oxford University Press; 2011. [Google Scholar]
- 106. Kingsley PB. Introduction to diffusion tensor imaging mathematics. Part I: Tensors, rotations, and eigenvectors. Conc Magn Reson A 2006;28A:101–122. [Google Scholar]
- 107. Bloembergen N, Rowland TJ. On the nuclear magnetic resonance in metals and alloys. Acta Metall 1953;1:731–746. [Google Scholar]
- 108. Pake GE. Nuclear resonance absorption in hydrated crystals: fine structure of the proton line. J Chem Phys 1948;16:327–336. [Google Scholar]
- 109. Laughlin RG. The aqueous phase behavior of surfactants. London: Academic Press; 1994. [Google Scholar]
- 110. Schnablegger H, Yashveer S. The SAXS guide: getting acquainted with the principles. Graz, Austria: Anton Paar GmbH; 2013. [Google Scholar]
- 111. Leal C, Sandström D, Nevsten P, Topgaard D. Local and translational dynamics in DNA‐lipid assemblies monitored by solid‐state and diffusion NMR. Biochim Biophys Acta, Biomembr 2008;1778:214–228. [DOI] [PubMed] [Google Scholar]
- 112. Xia Y. Relaxation anisotropy in cartilage by NMR microscopy (μMRI) at 14‐μm resolution. Magn Reson Med 1998;39:941–949. [DOI] [PubMed] [Google Scholar]
- 113. Momot KI, Pope JM, Wellard RM. Anisotropy of spin relaxation of water protons in cartilage and tendon. NMR Biomed 2010;23:313–324. [DOI] [PubMed] [Google Scholar]
- 114. Cohen‐Adad J, Polimeni JR, Helmer KG, Benner T, McNab JA, Wald LL, Rosen BR, Mainero C. T 2* mapping and B 0 orientation‐dependence at 7 T reveal cyto‐ and myeloarchitecture organization of the human cortex. NeuroImage 2012;60:1006–1014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115. Cohen‐Adad J. What can we learn from T 2* maps of the cortex? NeuroImage 2014;93 Pt 2:189–200. [DOI] [PubMed] [Google Scholar]
- 116. Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional kurtosis imaging: the quantification of non‐Gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med 2005;53:1432–1440. [DOI] [PubMed] [Google Scholar]
- 117. Szczepankiewicz F, van Westen D, Englund E, Westin C‐F, Ståhlberg F, Lätt J, Sundgren PC, Nilsson M. The link between diffusion MRI and tumor heterogeneity: mapping cell eccentricity and density by diffusional variance decomposition (DIVIDE). NeuroImage 2016;142:522–532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118. Lampinen B, Szczepankiewicz F, Mårtensson J, van Westen D, Sundgren PC, Nilsson M. Neurite density imaging versus imaging of microscopic anisotropy in diffusion MRI: a model comparison using spherical tensor encoding. NeuroImage 2017;147:517–531. [DOI] [PubMed] [Google Scholar]
- 119. McKeen LW. Permeability properties of plastics and elastomers. Norwich, NY: William Andrew; 2016. [Google Scholar]
- 120. Le TD, Olsson U, Mortensen K, Zipfel J, Richtering W. Nonionic amphiphilic bilayer structures under shear. Langmuir 2001;17:999–1008. [Google Scholar]
- 121. Lawson KD, Flautt TJ. Magnetically oriented lyotropic liquid crystalline phases. J Am Chem Soc 1969;89:5489–5491. [Google Scholar]
- 122. van der Spoel D, Lindahl E, Hess B, Groenhof G, Mark AE, Berendsen HJ. GROMACS: fast, flexible, and free. J Comput Chem 2005;26:1701–1718. [DOI] [PubMed] [Google Scholar]
- 123. POV‐Ray 3.7. http://www.povray.org. Last accessed January 15, 2017.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fig. S1. Parameter maps for all slices of the experimental data in Figure 4. The S 0, MD, and μFA maps were obtained with the gamma model, whereas the FA map is from standard DTI analysis. The gray scales have the same meanings as in Figure 4.
Fig. S2. Demonstration of the long‐time stability of the phantom. The data were acquired one year after the original measurements reported in Figure 4 and Supporting Figure S1 using the same scanner, experimental settings, and data‐processing pipeline. The phantom was stored at temperatures in the range from 19 to 24°C. The gray scales have the same meanings as in Figure 4. Note that the μFA maps remain uniform with values near unity.
Fig. S3. Application of the phantom on a conventional MR scanner. The data were acquired with the same phantom in Supporting Figure S2 using a conventional Siemens Magnetom Prisma 3T scanner with 0.080 Tm−1 maximum gradient strength and 200 Tm−1s−1 slew rate at a spatial resolution of 2.0 × 2.0 × 4.0 mm3 using an optimized acquisition protocol as described in 98. The data processing pipeline and visualization were the same as in Supporting Figure S1. Note the uniformity of the μFA maps with values near unity.
Table S1. Temperature Stability Range of the Reverse Hexagonal Phase for Samples With Chemical Compositions at and Around the Value Chosen for the Phantom.


