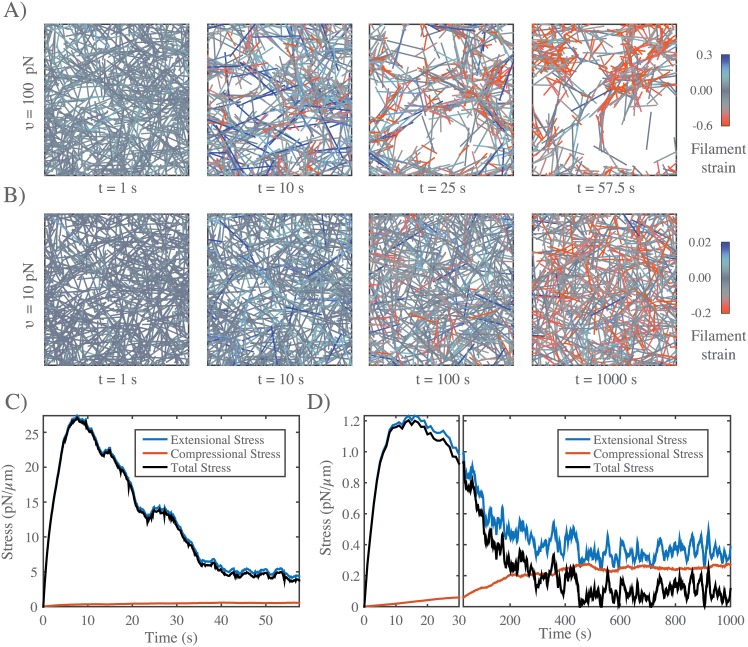
Fig 6. In the absence of filament turnover, active networks cannot sustain continuous stress against a fixed boundary.
A) Simulation of an active network with fixed boundaries. Rearrangement of network filaments by motor activity leads to rapid network fragmentation. Network parameters: L = 5 μm, lc = 0.3 μm, ξ = 100 pN ⋅ s/μm, υ = 100 pN. B) Simulation of the same network, with the same parameter values, except with ten-fold lower motor activity υ = 10 pN. In this case, the distribution of filaments remains more uniform, and network connectivity is maintained in the sense that each filament maintains overlap with many others. Note the progressive shift towards less extensional and greater compressional strain on individual filaments (see color map). C) Plots of total network stress and the average extensional (blue) and compressional (red) stress vs. time on individual filaments for the simulation shown in (A). Rapid buildup of extensional stress allows the network transiently to exert force on its boundary, but this force decays and this decay is closely associated with a decrease in extensional stress, reflecting the breakdown in network connectivity. D) Plots of total network stress and the average extensional (blue) and compressional (red) stress vs. time on individual filaments for the simulation shown in (b). Rapid buildup of extensional stress allows the network transiently to exert force on its boundary. However, stress decays at longer times as decreasing extensional stress and increasing compressional stress approach balance. Note the different time scales used for plots and subplots in C) and D) to emphasize the similar timescales for force buildup, but different timescales for force dissipation.