Abstract
It has been proposed that path integration in mammals is performed by the convergence of internally generated speed and directional inputs onto grid cells. Although this hypothesis has been supported by the discovery that head direction, speed, and grid cells are intermixed within entorhinal cortex and by the recent finding that head-direction inputs are necessary for grid firing, many details on how grid cells are generated have remained elusive. For example, analysis of recording data suggests that substituting head direction for movement direction accrues errors that preclude the formation of grid patterns. To address this discrepancy, we propose that the organization of grid networks makes it plausible that movement-direction signals are an output from grid cells and that temporally precise grid cell sequences provide a robust directional signal to other spatial and directional cell types.
Grid cells in the medial entorhinal cortex (mEC) were discovered by examining the firing patterns of entorhinal cell populations that project to hippocampal place cells [1,2]. As a consequence, the initial focus of computational models was on the spatial information that entorhinal grid cells could provide to hippocampal place cells or, more generally, to a map-like representation of the environment [3,4]. However, the tessellating nature of grid cells also suggested that they may not only be the source of spatial information for a map-based navigation system, but that they might themselves be at the core of a specialized path integration-based navigation system, which is particularly well suited to code for locations and distances in the absence of prominent landmarks [2,4,5].
Updating of current location by direction and speed signals
Path integration (or dead reckoning) requires that direction and speed (or distance) signals are integrated to update the current position in relation to a reference position [6]. Computational models of grid cells therefore began to examine neuronal mechanisms that are capable of generating grid patterns from the convergence of speed and direction inputs (Fig. 1). The integration of these two types of afferent signals was initially proposed to be performed within single grid cells [5], but implementation of these computations in neuronal networks was also considered for a number of reasons. First, the reliance of brain systems on internally integrated movement signals is limited by error accumulation, which can be effectively reduced by combining individual noisy signals into a larger network [7]. Second, experimental work identified that head-direction cells, conjunctive grid by direction cells, and speed cells provide local inputs to grid cell networks [8,9], which is consistent with a number of feedforward and/or recurrent neural network architectures that combine inputs of these cell types with local network computations [10,11]. For example, based on the finding that head direction cells and conjunctive direction by grid cells are preferentially found in deep layers and that grid cells without directional preference are found in layer II [8], many models explicitly include connectivity between different cell types within mEC to perform network computations [12].
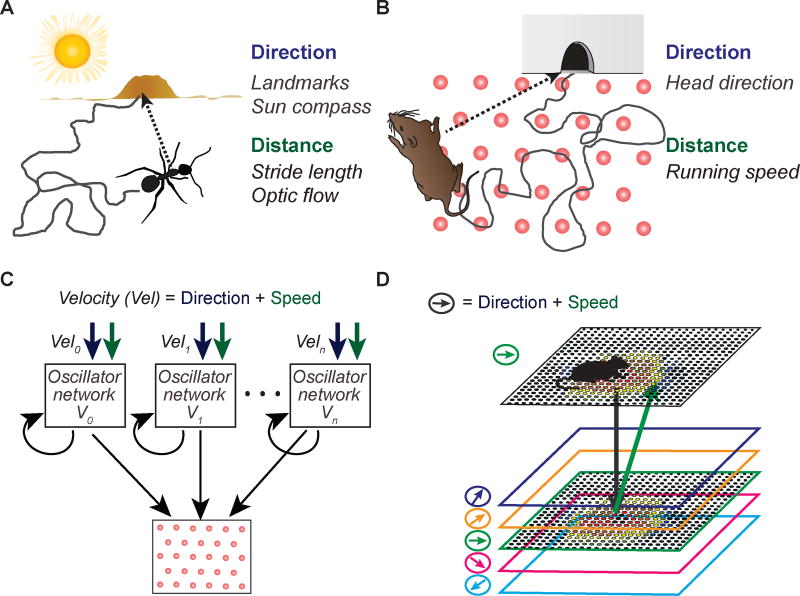
Figure 1. Multiple mechanisms for the implementation of path integration.
(A) Path integration mechanisms for mammalian species such as rodents, who forage under conditions with sparse visual and landmark cues, have been proposed to predominantly rely on internally generated estimates of speed and direction. The internal direction and distance estimates are integrated by grid cells, which could provide a path-integration based estimate of the current position. Here, direction signals are assumed to be provided by internally generated head direction cells, and distance is computed using internally generated speed signals that also manifest within the brain. (B) One major class of grid cell generation models are the oscillatory interference models [5,7]. In this class of models, signals are integrated by velocity controlled oscillators that receive head direction and speed inputs. Grid cells receive information from multiple oscillators that each respond to a different direction. Coincident peak phases of activity result in grid cell firing, whereas cells remain silent when the oscillators are out of phase with each other. Adapted from [4,7]. (C) The other major class of grid cell generation models are continuous attractor network models, which generate grid patterns from local recurrent network connectivity. Depicted here is one such implementation [4]. Excitatory and inhibitory connections between cells lead to a ‘bump’ of focused activity in the network, which is gradually moved in the cell sheet by directional and speed signals. Adapted from [4,7].
Because the implementation of neuronal computations that give rise to grid cells has been extensively considered and reviewed [10,11], we will focus on recent progress in identifying potential sources for directional and speed signals to grid cells as well as on recent work that has challenged the assumption that head-direction signals can be used interchangeably with movement-direction information in grid cell models [13]. Furthermore, based on work that has not identified any substantive movement-direction signals in mEC [13], we consider the possibility that movement direction coding is only weakly provided as an input to grid cells and emerges as a robust temporal code from grid cell network activity. This mechanism implies that directional information is also an output from grid cells while many standard grid cell models only consider it as an input [14].
Head-direction signals are not sufficient as ongoing inputs to grid networks
Each grid cell generates neuronal activity at multiple, regularly arranged spatial locations [2]. When these spatial firing patterns are updated over seconds and minutes by path integration, the internally generated running speed and direction signal both need to be highly accurate. For the speed signal, three possible sources have been identified as highly correlated with running speed and could therefore each provide a reliable speed input [9,15–17] (Fig. 2). As a directional signal for grid cells, sharply tuned head-direction cells, which arise from the processing of signals from vestibular nuclei, have been considered as a reliable source [18]. Even though head direction is known to be reliably represented in the brain, there is limited knowledge on the modulation of the head-direction code by additional internal directional movements, such as eye movements or rotation of the head with respect to the body axis. For example, deviation of the head angle from the body axis could be derived from the disparity in optic flow that arises as a consequence of the mismatch between head and movement direction [13] or, more directly, from proprioceptors in neck muscles. Based on studies that detected a movement direction signal in the medial septal area [19,20], it is possible that integration occurs in subcortical areas, but again, these studies have not explored to what extent head direction and movement direction are coded jointly or separately.
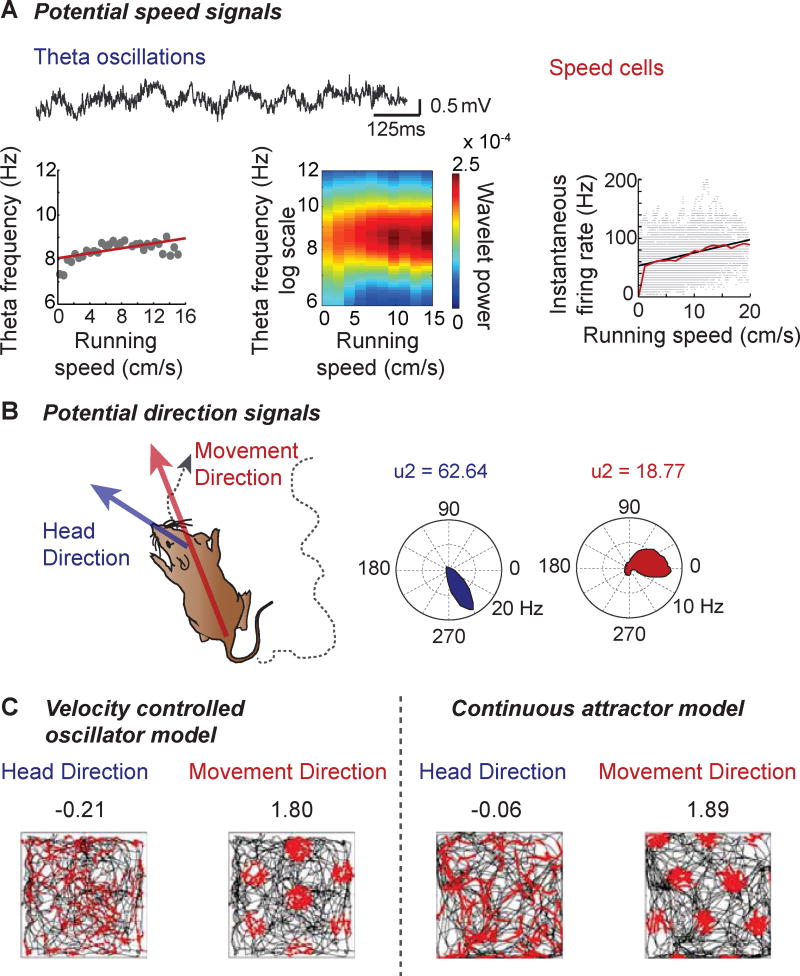
Figure 2. Sources of speed and direction information for path integration in rodents.
(A) Speed information is internally represented in rodents by at least three possible mechanisms. Left, the frequency of theta oscillations is modulated by the running speed of an animal. Middle, in addition to changes in theta frequency, the amplitude or power of theta oscillations is also positively correlated with increasing running speed, as depicted in the spectrogram where increasing power is shown on a scale from blue to red. Right, speed cells have been found in mEC [9]. As shown in the example, most speed cells increase their firing rate with increased running speed. (B) Movement direction is assumed resemble head direction signals, which are found in several brain areas, including mEC. However, the schematic on the left depicts how for every instant during foraging, head direction can be distinct from direction of movement. As a result of this incongruity, a single cell that is strongly tuned to the head direction of an animal (blue) provides a conflicting and more broadly tuned signal for movement direction (red). Watson U2 measures are provided above each polar plot. Note that the strength of movement tuning in the example is exceptionally high compared to other mEC cells. Adapted from [13]. (C) Using pure head direction signals, instead of movement direction signals in grid cell models results in rapid breakdown of grid cells due to the disparity between the two signals. Shown here are two examples of grid cells that were reconstructed with either a velocity controlled oscillator model or a continuous attractor network implementation (see Fig. 1). Gridness scores for each example are provided on top of each plot. Neither model supports grid cell generation when a head direction signal is provided, which suggests that head direction cannot substitute for movement direction in path integration computations. Adapted from [13].
Because of the uncertainty in where and how a movement-direction signal is coded in the brain, many computational models have used the head-direction signal interchangeably with a movement-direction signal, based on the assumption that the head direction is a good approximation for movement direction. However, it has recently been found in analytical work that grid patterns can only emerge when using the recorded movement direction of the animal as an input to computational networks, but not when substituting the recorded head direction of the animal [13]. Alternatively, computational models have proposed that directional information is received from stripe cells [5,21]. However, the proportion of stripe cells is low [22] and their existence is controversial because they could be obtained from the incomplete separation of the spike patterns of two grid cells [23].
The broad use of a head-direction signal in models for grid generation is also motivated by the presence of head direction cells and of conjunctive head-direction by grid cells in mEC, which has been taken as evidence that head-direction signals are integrated into the local neuronal codes [8]. Furthermore, recent experimental evidence has shown that the grid network depends on input from the brain’s head-direction system [24]. Although these findings can be interpreted as supporting the notion that head-direction input is critical for grid generation, these data need to be reconciled with the finding that head-direction coding is not sufficient for maintaining grid patterns [13]. Several possibilities are mentioned here which are not mutually exclusive. First, movement and head-direction may be jointly coded and may thus not have been independently manipulated [24]. Second, manipulations of thalamic head-direction may have resulted in minor effects on theta oscillations. Theta oscillations are, in turn, known to contribute to speed as well as to directional coding [15,19,20], such that speed and head-direction coding may again not have been independently manipulated. Third, manipulations of thalamic nuclei resulted in reduced firing rates of entorhinal cells, which in turn, is expected to result in diminished grid patterns in many computational models that rely on afferent and recurrent connectivity [10,11]. Although the diminished grid coding after inactivation of the head-direction system therefore strongly implies head-direction coding in grid generation, the finding of a strong disparity between the movement and head direction code [13] raises the possibility that the head-direction code would need to be complemented by other directional signals or additional sensory pathways to correct for the moment-by-moment errors that arise from exclusively relying on head-direction inputs.
Where and how could a movement-direction signal be generated?
The finding that a movement-direction signal is required for grid cell generation by path integration, along with limited evidence for movement-direction coding by entorhinal cells [13] raises the question about the nature and origin of the movement-direction signal (or a signal that corrects the disparity between head-direction and movement-direction) in mEC. Although a movement-direction signal could emerge from directionally tuned coupling of oscillations in the medial septal area [19,20] or from not-yet-identified sensory processing of proprioceptive and/or optic flow information, we propose that an alternative hypothesis should also be considered. A robust movement-direction signal could be obtained from the readout of temporal sequences of grid cell activation (Fig. 3). In particular, the modular arrangement of grid cells results in a limited number of grid cell sequences that are associated with each movement direction such that a finite set of grid sequences can be combined to represent a particular direction (Fig. 3). Because the highly modular organization of mEC grid cell populations is a prerequisite of the proposed mechanism, we will give a brief overview of the modular grid cell organization and then describe in more detail how the regularity within each module supports the readout of movement-direction information.
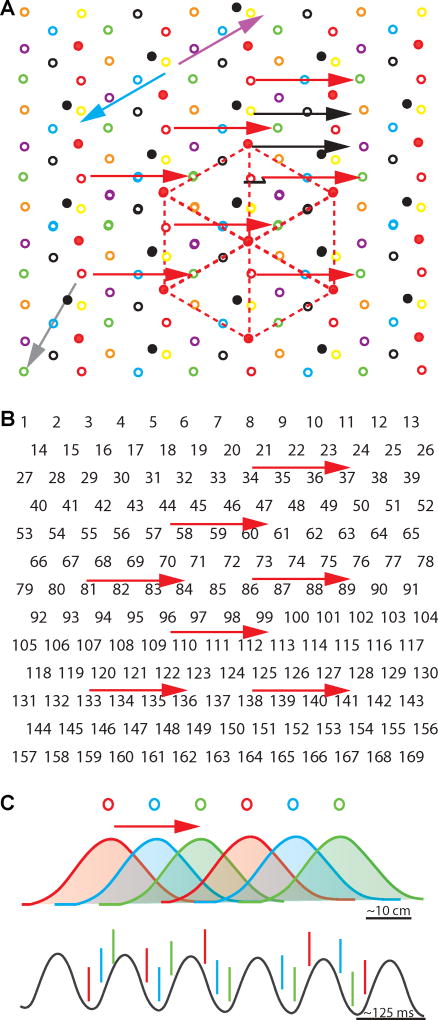
Figure 3. A finite number of grid cell sequences is associated with each movement direction.
(A) In a lattice of grid field peaks, grid peaks that belong to the same grid cell are shown with a consistent symbol (e.g., red solid circle; the stippled lines between grid peaks of this cell illustrate the grid spacing within the module). By showing only grid field peaks, the consistent spacing and orientation of multiple grid cells within a module as well as the fixed offsets between peaks of different cells are apparent. For the illustration, the offsets between the depicted grid peaks have generally been chosen to occur at regular distances, but note that offsets between fields can be at any distance in experimental data [2,25] (e.g., as shown for the grid cell depicted by the filled black circle). Red arrows, within the lattice of peaks, the same movement direction repeatedly corresponds to the same sequence of cells (e.g., open red then blue then green circles). Grey arrow, if a movement direction were represented by too few grid cells, there could be ambiguity for directions that are offset by 120 degrees. However, the inclusion of additional cells in the sequence code (e.g., the one depicted by black filled circles) resolves the ambiguity. Purple and green arrows, the same cells fire for sequences in opposite directions, but the order of the cell activity is reversed. Black and red arrows, multiple sequences code for the same movement direction. However, there is only a limited set of sequences for each direction because of the repetitive nature of the grid lattice. (B) Each number depicts the peak of a hippocampal place field within a 2-D environment. Note that the lack of regularly repeated firing fields results in a different sequence for each combination of movement direction and starting point. Coding with non-repetitive representation is therefore better suited for representing specific trajectories rather than movement direction. (C) Phase precession results in the time-compression of sequences [45], and the sequence of phase precessing grid cells within a theta cycle can be used for the readout of the current movement direction. As shown in the example, sequences have different start and end points depending on the position of the animal along the trajectory, but identical sequences will eventually repeat for trajectories with corresponding movement directions. (D) Schematic in which inputs to the entorhinal cortex give rise to speed, head-direction, and spatially selective cells, but only to limited modulation of cells by movement-direction (grey text implies that this information is initially more weakly represented). All types of information are locally processed, and sequential coding of movement direction emerges as an output from grid cells that could be read out by other spatially and directionally selective cells within entorhinal cortex and hippocampus. EC, entorhinal cortex. Hpc, hippocampus.
Modular organization of the grid network
Grid cells have been estimated to be organized into less than ten modules per hemisphere [25]. The modules are topographically organized with partial anatomical overlap between two adjacent modules. Each module consists of grid cells with similar field size, grid spacing and grid orientation. Modules with smaller grid spacing and grid field size are more dorsal within mEC, while those with larger grid spacing and grid field size are generally more ventral. The only parameter that varies between grid cells within a module is the spatial firing phase, such that all firing peaks between pairs of grid cells are offset by a fixed distance (Fig. 3). The common grid spacing and orientation as well as the phase offset between different grid cells in a module are not only preserved within an environment, but also across environments. In correspondence with these experimental findings, the organization of grid cells into populations with equal spacing is a foundational feature of many computational network models for grid cell generation [26,27]. For models in which grid patterns initially emerge separately in individual cells, common orientation can be added through connectivity between grid cells [11].
While the organization of grids into modules with equal spacing and orientation makes the organization of grid cells extremely intriguing [2,25], the regularity has also been found to somewhat hamper the readout of location information from populations of grid cells. If only reading information from a single grid module, the equal spacing and orientation implies that the population code of grid cells in the module repeats at the scale of the grid spacing within the module (Fig. 3). The ambiguity about spatial location can be resolved by reading from multiple grid modules [3,28], by using the recently discovered rate code within grid cells [29], or by using the spatial and rate code of the large spatial non-grid population in mEC [29,30]. In contrast, if grid cells within a module are used to read out a movement-direction code, the regularity is highly advantageous, as it results in a limited number of sequences that are associated with each movement direction (Fig. 3A).
The regularity of the grid cell organization within each module results in a finite set of sequences that correspond to each movement direction
While the fixed grid size and orientation within a module results in ambiguity in the readout of position, the fixed arrangement is advantageous for the readout of movement direction. The repetitive nature of grid representation would greatly reduce the number of sequences that are associated with each movement direction (Fig. 3B). Accordingly, the tessellation of the environment by grid fields implies that readout mechanism would only need to learn a limited number of possibilities within each environment. Furthermore, phase differences between grid cells within a module are preserved across environments [25], and the movement-direction code from each module would thus directly transfer to new and distinct environments. Because different modules can realign with respect to each other across environments, the only parameter that would need to be relearned for decoding movement direction across different environments is the relative rotation between pairs of modules.
A temporal code allows for the readout of movement direction within short time windows
Because of frequent changes in movement direction, a neural code for movement direction should be readable within a short time window. It is therefore relevant to note that many grid cells in rodents show theta phase precession, in particular those that are not modulated by head direction [31]. Phase precession implies that grid fields that are being entered by the animal fire at a late phase within the theta cycle while grid fields that are exited fire early within the cycle (Fig. 3C). As a consequence, the grid cells with fields just behind and just ahead of the animal fire within a single theta cycle in the order that corresponds to their direction of traversal and thus to movement direction. Within each theta cycle, there is therefore a sequence of spikes that identifies the movement progression within the grid lattice.
Using theta sequences as a mechanism for reading out movement-direction information from grid cells raises questions about animal species in which theta is either intermittent or not detectible, such as primates and bats [32,33]. First, sequences of grid cell firing along the movement trajectory would nonetheless exist, but would need to be decoded from the spatial rather than from the temporal sequence of the grid fields that are traversed. This mechanism is adequate if travelling in a particular direction for distances that correspond to approximately the minimum grid spacing. In lieu of a mechanism that relies on an internal sense of direction, it could also be speculated that an internally generated movement direction signal may not be necessary when external landmarks (e.g., a sun compass, distal cues) are prominent and can provide a consistent directional reference, as often observed for navigation over long distances [34].
How are head-direction and movement-direction signals integrated?
If grid patterns provide movement-direction information, two important questions arise. First, how are grid cells initially generated while head-direction input is more prominent than movement-direction input? Second, how are grid locations updated if head-direction input is not sufficiently precise? For the first question, we refer to the many published models on grid generation [10,11], including those that use head-direction inputs. Even though the head-direction input may not correspond to movement direction on a moment by moment basis, there is likely a good correspondence on average such that disparities are corrected by learning over long time periods, consistent with the emergence of grid cells within days after pups start exploring environments [35,36]. However, this mechanism would only be feasible if the network learns slow enough to integrate over the differences between the head direction and movement direction and if an animal’s head position compared to its body axis is not biased over long intervals. As an alternative, a weak movement-direction signal could emerge from the medial septal area [19,20] or from sensory channels in which proprioceptive and/or optic flow information are processed. Finally, it is also feasible that grid cells emerge by mechanisms that require only inputs from location-selective cells [37]. The second question – updating the location of grid firing – can also be addressed by the close association of grid cells with location-selective cells, which includes spatial non-grid cells within entorhinal cortex [29] and inputs from hippocampal place cells [38]. In particular, grid cells have been shown to develop after an increasingly accurate hippocampal input has been established [39] and have been shown to depend on hippocampal input [38]. In addition, it has long been known that a strong directional signal is present in hippocampal place populations which represent a path through the environment [40], and direction selectivity becomes even more predominant in virtual environments [41]. However, these directional signals are highly specific for particular environments because different hippocampal cell populations are active across environments [42]. Furthermore, the directional signals would differ with each starting position within 2D environments (Fig. 3B). These considerations make the transformation from environment-specific or behavior-specific hippocampal maps to a more generalized entorhinal map attractive, because only the more generalized map has a limited number of sequences associated with each direction. However, it remains to be tested whether and how a readout of movement direction from grid cells could be used by other cell types and brain regions that process spatial information. If spatial information from hippocampal place cells or other cells with allocentric spatial information is required to generate grid cells in the first place, the animal’s current position would already have been updated in input channels to grid cells. With allocentric information already available to grid cells, directional information from grid cells may nonetheless be useful for navigation across zones with few landmarks, for calibrating a sensory-based spatial map in each novel environment to the animal’s own movement patterns, and/or for predicting which future locations are reached when travelling or planning particular movement trajectories [43,44]. Moreover, grid cells could also have the function of transforming weakly tuned movement direction signals in mEC into a more robust sequence code for movement direction. Under this condition, grid cells would be the primary path integrators but other cells in the circuit would also path integrate by combining the movement direction and speed signals from entorhinal grid and speed cells.
Conclusions
Although it has been widely assumed that head-direction cells provide one of the critical inputs for path integration by grid cells, head direction information has been found to be insufficient for providing a reliable moment-by-moment estimate of movement direction [13] such that accurate path integration is at least in some circumstances not performed by exclusively relying on head direction signals. Alternative mechanisms are therefore needed, and we evaluated the possibility that information from grid cell networks could generate a movement-direction signal. We propose that the highly modular organization of grid cell populations [25] provides for a limited number of sequences that correspond to each movement direction irrespective of the starting point within the environment. These sequences can be read out when running in the same direction for approximately one grid cycle or, in neural systems with phase precession, on the shorter time-scale of a single theta cycle. Although this mechanism does not exclude the possibility that grid cells receive movement-direction information by not-yet-identified feedforward pathways, we propose that the direction of a movement trajectory could also be obtained from the readout of theta sequences or spatial sequences of grid cells.
Highlights.
Substituting head direction for movement direction accrues errors that preclude grid patterns.
Only weak movement-direction signals have been identified in mEC
Movement-direction could be coded by a temporal rather than a rate code.
Grid cell sequences can serve as a movement-direction signal to other cell types.
Acknowledgments
This work was supported by the National Institute of Health [MH100354, NS084324, NS086947, MH100349, NS102915, NS097772], the Whitehall Foundation [20130571], Walter F. Heiligenberg Professorship to J.K.L, and an HHMI International Student Fellowship to I. Z.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
The authors declare no competing financial interests.
References
- 1.Fyhn M, Molden S, Witter MP, Moser EI, Moser MB. Spatial representation in the entorhinal cortex. Science. 2004;305:1258–1264. doi: 10.1126/science.1099901. [DOI] [PubMed] [Google Scholar]
- 2.Hafting T, Fyhn M, Molden S, Moser MB, Moser EI. Microstructure of a spatial map in the entorhinal cortex. Nature. 2005;436:801–806. doi: 10.1038/nature03721. [DOI] [PubMed] [Google Scholar]
- 3.Solstad T, Moser EI, Einevoll GT. From grid cells to place cells: a mathematical model. Hippocampus. 2006;16:1026–1031. doi: 10.1002/hipo.20244. [DOI] [PubMed] [Google Scholar]
- 4.McNaughton BL, Battaglia FP, Jensen O, Moser EI, Moser MB. Path integration and the neural basis of the 'cognitive map'. Nat Rev Neurosci. 2006;7:663–678. doi: 10.1038/nrn1932. [DOI] [PubMed] [Google Scholar]
- 5.Burgess N, Barry C, O'Keefe J. An oscillatory interference model of grid cell firing. Hippocampus. 2007;17:801–812. doi: 10.1002/hipo.20327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wolf H. Odometry and insect navigation. J Exp Biol. 2011;214:1629–1641. doi: 10.1242/jeb.038570. [DOI] [PubMed] [Google Scholar]
- 7.Zilli EA, Hasselmo ME. Coupled noisy spiking neurons as velocity-controlled oscillators in a model of grid cell spatial firing. J Neurosci. 2010;30:13850–13860. doi: 10.1523/JNEUROSCI.0547-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sargolini F, Fyhn M, Hafting T, McNaughton BL, Witter MP, Moser MB, Moser EI. Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science. 2006;312:758–762. doi: 10.1126/science.1125572. [DOI] [PubMed] [Google Scholar]
- 9.Kropff E, Carmichael JE, Moser MB, Moser EI. Speed cells in the medial entorhinal cortex. Nature. 2015;523:419–424. doi: 10.1038/nature14622. •• While several grid cell models require the existance of local speed signals to provide accurate distance estimates, it had been unclear whether such a signal existed in mEC. This study discovered mEC cells that modulate their firing rate with the running speed of an animal. These speed cells are invariant to changes in context and therefore could provide reliable speed information to grid cells. [DOI] [PubMed] [Google Scholar]
- 10.Giocomo LM, Moser MB, Moser EI. Computational models of grid cells. Neuron. 2011;71:589–603. doi: 10.1016/j.neuron.2011.07.023. [DOI] [PubMed] [Google Scholar]
- 11.Zilli EA. Models of grid cell spatial firing published 2005–2011. Front Neural Circuits. 2012;6:16. doi: 10.3389/fncir.2012.00016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tocker G, Barak O, Derdikman D. Grid cells correlation structure suggests organized feedforward projections into superficial layers of the medial entorhinal cortex. Hippocampus. 2015;25:1599–1613. doi: 10.1002/hipo.22481. [DOI] [PubMed] [Google Scholar]
- 13.Raudies F, Brandon MP, Chapman GW, Hasselmo ME. Head direction is coded more strongly than movement direction in a population of entorhinal neurons. Brain Res. 2015;1621:355–367. doi: 10.1016/j.brainres.2014.10.053. •• By analyzing head direction and movement direction of an animal during random foraging, this study addresses whether these two direction signals are coded distinctly in mEC. While head direction was strongly respresented by mEC cells, only sparse movement direction signals were found. The authors then implemented grid cell models with either a movement direction signal or a head direction signal and found that grid firing could only be sustained with a movement direction signal. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Finkelstein A, Las L, Ulanovsky N. 3-D Maps and Compasses in the Brain. Annu Rev Neurosci. 2016;39:171–196. doi: 10.1146/annurev-neuro-070815-013831. [DOI] [PubMed] [Google Scholar]
- 15.Hinman JR, Brandon MP, Climer JR, Chapman GW, Hasselmo ME. Multiple Running Speed Signals in Medial Entorhinal Cortex. Neuron. 2016;91:666–679. doi: 10.1016/j.neuron.2016.06.027. •• This study builds upon previous studies that have demonstrated that inactivation of the medial septal area (MSA) leads to a drastic loss in theta oscillations, which are modulated by running speed. Here, the authors examine how speed cells in mEC are affected by MSA inactivation, and address whether a loss in theta leads to a concomitant loss in speed cell tuning. The authors report a surprising increase in speed tuning during MSA inactivation, suggesting that theta oscillations and mEC speed cells provide independent and distinct speed signals. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jeewajee A, Barry C, O'Keefe J, Burgess N. Grid cells and theta as oscillatory interference: electrophysiological data from freely moving rats. Hippocampus. 2008;18:1175–1185. doi: 10.1002/hipo.20510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kemere C, Carr MF, Karlsson MP, Frank LM. Rapid and continuous modulation of hippocampal network state during exploration of new places. PLoS One. 2013;8:e73114. doi: 10.1371/journal.pone.0073114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Taube JS. The head direction signal: origins and sensory-motor integration. Annu Rev Neurosci. 2007;30:181–207. doi: 10.1146/annurev.neuro.29.051605.112854. [DOI] [PubMed] [Google Scholar]
- 19.King C, Recce M, O'Keefe J. The rhythmicity of cells of the medial septum/diagonal band of Broca in the awake freely moving rat: relationships with behaviour and hippocampal theta. Eur J Neurosci. 1998;10:464–477. doi: 10.1046/j.1460-9568.1998.00026.x. [DOI] [PubMed] [Google Scholar]
- 20.Welday AC, Shlifer IG, Bloom ML, Zhang K, Blair HT. Cosine directional tuning of theta cell burst frequencies: evidence for spatial coding by oscillatory interference. J Neurosci. 2011;31:16157–16176. doi: 10.1523/JNEUROSCI.0712-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Grossberg S, Pilly PK. How entorhinal grid cells may learn multiple spatial scales from a dorsoventral gradient of cell response rates in a self-organizing map. PLoS Comput Biol. 2012;8:e1002648. doi: 10.1371/journal.pcbi.1002648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Krupic J, Burgess N, O'Keefe J. Neural representations of location composed of spatially periodic bands. Science. 2012;337:853–857. doi: 10.1126/science.1222403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Navratilova Z, Godfrey KB, McNaughton BL. Grids from bands, or bands from grids? An examination of the effects of single unit contamination on grid cell firing fields. J Neurophysiol. 2016;115:992–1002. doi: 10.1152/jn.00699.2015. [DOI] [PubMed] [Google Scholar]
- 24.Winter SS, Clark BJ, Taube JS. Spatial navigation. Disruption of the head direction cell network impairs the parahippocampal grid cell signal. Science. 2015;347:870–874. doi: 10.1126/science.1259591. •• Head direction signals to the parahippocampal area were abolished by lesioning or inactivating the anterior thalamic nucleus. Both manipulations resulted in a profound reduction in firing rate and directional tuning of head direction cells in the mEC, along with a corresponding reduction in firing rate and grid periodicity of grid cells. These results suggests that brain areas that are associated with the head direction signals provide necessary information to the grid cell system. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Stensola H, Stensola T, Solstad T, Froland K, Moser MB, Moser EI. The entorhinal grid map is discretized. Nature. 2012;492:72–78. doi: 10.1038/nature11649. [DOI] [PubMed] [Google Scholar]
- 26.Burak Y, Fiete IR. Accurate path integration in continuous attractor network models of grid cells. PLoS Comput Biol. 2009;5:e1000291. doi: 10.1371/journal.pcbi.1000291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Fuhs MC, Touretzky DS. A spin glass model of path integration in rat medial entorhinal cortex. J Neurosci. 2006;26:4266–4276. doi: 10.1523/JNEUROSCI.4353-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Stemmler M, Mathis A, Herz AV. Connecting multiple spatial scales to decode the population activity of grid cells. Sci Adv. 2015;1:e1500816. doi: 10.1126/science.1500816. •• Based on the discovery that grid cells are organized into modules with discrete spacing, this study examines in detail how to decode spatial information from grid networks with common grid spacing within modules, but distinct grid spacing between modules. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Diehl GW, Hon OJ, Leutgeb S, Leutgeb JK. Grid and Nongrid Cells in Medial Entorhinal Cortex Represent Spatial Location and Environmental Features with Complementary Coding Schemes. Neuron. 2017 doi: 10.1016/j.neuron.2017.03.004. •• This study finds that most non-grid cells in mEC show spatial tuning, but that their spatial tuning is altered with minor manipulations of environmental features. Spatial reorganization of non-grid cells therefore occurs while the spatial representation of grid cells are stable, and spatially stable grid cells show a redistribution of firing rates between grid fields. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kanter BR, Lykken CM, Avesar D, Weible A, Dickinson J, Dunn B, Borgesius NZ, Roudi Y, Kentros CG. A Novel Mechanism for the Grid-to-Place Cell Transformation Revealed by Transgenic Depolarization of Medial Entorhinal Cortex Layer II. Neuron. 2017;93:1480–1492 e1486. doi: 10.1016/j.neuron.2017.03.001. •• This study finds that rate changes in layer II, even in the absence of spatial reorganization of the cells' firing patterns, are sufficient to induce remapping of hippocampal place cells. Although the title of the publication focuses on grid cells, their manipulations affected grid and non-grid cells in mEC layer II. [DOI] [PubMed] [Google Scholar]
- 31.Hafting T, Fyhn M, Bonnevie T, Moser MB, Moser EI. Hippocampus-independent phase precession in entorhinal grid cells. Nature. 2008;453:1248–1252. doi: 10.1038/nature06957. [DOI] [PubMed] [Google Scholar]
- 32.Yartsev MM, Witter MP, Ulanovsky N. Grid cells without theta oscillations in the entorhinal cortex of bats. Nature. 2011;479:103–107. doi: 10.1038/nature10583. [DOI] [PubMed] [Google Scholar]
- 33.Jutras MJ, Fries P, Buffalo EA. Oscillatory activity in the monkey hippocampus during visual exploration and memory formation. Proc Natl Acad Sci U S A. 2013;110:13144–13149. doi: 10.1073/pnas.1302351110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bingman VP, MacDougall-Shackleton SA. The avian hippocampus and the hypothetical maps used by navigating migratory birds (with some reflection on compasses and migratory restlessness) J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2017 doi: 10.1007/s00359-017-1161-0. [DOI] [PubMed] [Google Scholar]
- 35.Wills TJ, Cacucci F, Burgess N, O'Keefe J. Development of the hippocampal cognitive map in preweanling rats. Science. 2010;328:1573–1576. doi: 10.1126/science.1188224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Langston RF, Ainge JA, Couey JJ, Canto CB, Bjerknes TL, Witter MP, Moser EI, Moser MB. Development of the spatial representation system in the rat. Science. 2010;328:1576–1580. doi: 10.1126/science.1188210. [DOI] [PubMed] [Google Scholar]
- 37.Kropff E, Treves A. The emergence of grid cells: Intelligent design or just adaptation? Hippocampus. 2008;18:1256–1269. doi: 10.1002/hipo.20520. [DOI] [PubMed] [Google Scholar]
- 38.Bonnevie T, Dunn B, Fyhn M, Hafting T, Derdikman D, Kubie JL, Roudi Y, Moser EI, Moser MB. Grid cells require excitatory drive from the hippocampus. Nat Neurosci. 2013;16:309–317. doi: 10.1038/nn.3311. [DOI] [PubMed] [Google Scholar]
- 39.Muessig L, Hauser J, Wills TJ, Cacucci F. A Developmental Switch in Place Cell Accuracy Coincides with Grid Cell Maturation. Neuron. 2015;86:1167–1173. doi: 10.1016/j.neuron.2015.05.011. •• This study directly compares the time course of place cell and grid cell maturation during development. They find that place cell accuracy increases gradually while grid cells emerge suddenly at a time when place cell accuracy approaches levels that are comparable to adults. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.McNaughton BL, Barnes CA, Gerrard JL, Gothard K, Jung MW, Knierim JJ, Kudrimoti H, Qin Y, Skaggs WE, Suster M, et al. Deciphering the hippocampal polyglot: the hippocampus as a path integration system. J Exp Biol. 1996;199:173–185. doi: 10.1242/jeb.199.1.173. [DOI] [PubMed] [Google Scholar]
- 41.Aghajan ZM, Acharya L, Moore JJ, Cushman JD, Vuong C, Mehta MR. Impaired spatial selectivity and intact phase precession in two-dimensional virtual reality. Nat Neurosci. 2015;18:121–128. doi: 10.1038/nn.3884. [DOI] [PubMed] [Google Scholar]
- 42.Leutgeb S, Leutgeb JK, Treves A, Moser MB, Moser EI. Distinct ensemble codes in hippocampal areas CA3 and CA1. Science. 2004;305:1295–1298. doi: 10.1126/science.1100265. [DOI] [PubMed] [Google Scholar]
- 43.Sanders H, Renno-Costa C, Idiart M, Lisman J. Grid Cells and Place Cells: An Integrated View of their Navigational and Memory Function. Trends Neurosci. 2015;38:763–775. doi: 10.1016/j.tins.2015.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Renno-Costa C, Tort ABL. Place and grid cells in a loop: implications for memory function and spatial coding. J Neurosci. 2017 doi: 10.1523/JNEUROSCI.3490-16.2017. •• This pioneering study combines place cell and grid cell models and also includes spatial non-grid cells to examine spatial coding in the entorhino-hippocampal loop. The integration of these cell types into a single model reproduces key experimental manipulations of entorhinal and hippocampal cells, and shows that an advantage of parallel spatial representations is their robustness to noisy and inconsistent input conditions. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Dragoi G, Buzsaki G. Temporal encoding of place sequences by hippocampal cell assemblies. Neuron. 2006;50:145–157. doi: 10.1016/j.neuron.2006.02.023. [DOI] [PubMed] [Google Scholar]