Fig. 2.
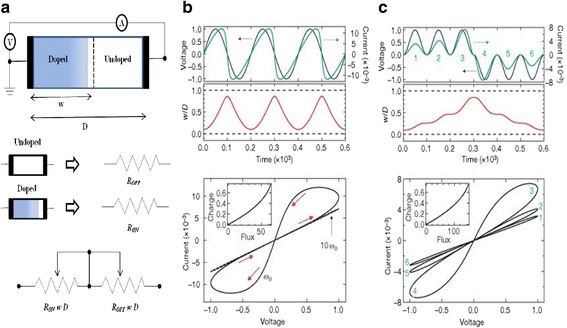
The coupled variable-resistor model for a memristor is presented. a A simplified equivalent circuit comprising of a (V) voltmeter and (A) ammeter. b, c The applied voltage (blue) and resulting current (green) as a function of time t for a typical memristor are also presented. In b the applied voltage is v0 sin(v0t) and the resistance ratio is ROFF/RON = 160, and in c the applied voltage is ±v0 sin2(ω0t) and ROFF/RON = 380, where ω0 is the frequency and v0 is the magnitude of the applied voltage. The numbers 1–6 are labeled for successive waves in the applied voltage and the corresponding loops in i–v curves. In each plot, the axes are dimensionless, with voltage, current, time, flux, and charge expressed in units of v0 = 1 V, i0 ≡ v0/RON = 10 mA, t0 ≡ 2π/ω0 ≡ D2/μvv0 = 10 m/s, v0t0 and i0t0, respectively. The term i0 denotes the maximum possible current through the device, and t0 is the shortest time required for linear drift of dopants across the full device length in a uniform field v0/D, for example with D = 10 nm and μV = 10−10 cm2 s−1 V−1. It is to be noted that for the parameters chosen, the applied bias never forces either of the two resistive regions to collapse; for example, w/D does not approach zero or one (shown with dashed lines in the middle plots in b and c). Also, the dashed i–v plot in b demonstrates the hysteresis collapse observed with a tenfold increase in sweep frequency. The insets of i–v plots in b and c show that for these examples, the charge is a single-valued function of the flux, as it must be in a memristor [3]
