Why is parental lifespan linked to children's chances of reaching a high age? A transgenerational hypothesis

Abstract

Purpose

Transgenerational determinants of longevity are poorly understood. We used data from four linked generations (G0, G1, G2 and G3) of the Uppsala Birth Cohort Multigeneration Study to address this issue.

Methods

Mortality in G1 (N = 9565) was followed from 1961–2015 and analysed in relation to tertiles of their parents’ (G0) age-at-death using Cox regression. Parental social class and marital status were adjusted for in the analyses, as was G1’s birth order and adult social class. For an almost entirely deceased segment of G1 (n = 1149), born 1915–1917, we compared exact age-at-death with G0 parents’ age-at-death. Finally, we explored ‘resilience’ as a potentially important mechanism for intergenerational transmission of longevity, using conscript information from psychological interviews of G2 and G3 men.

Results

G0 men’s and women’s ages-at-death were independently associated with G1 midlife and old age mortality. This association was robust and minimally reduced when G0 and G1 social class were adjusted for. We observed an increased lifespan in all social groups. Median difference in age-at-death for sons compared to fathers was + 3.9 years, and + 6.9 years for daughters compared to mothers.

Parents’ and maternal grandmother’s longevity were associated with resilience in subsequent generations. Resilience scores of G2 men were also associated with those of their G3 sons and with their own mortality in midlife.

Conclusions

The chance of reaching a high age is transmitted from parents to children in a modest, but robust way. Longevity inheritance is paralleled by the inheritance of individual resilience. Individual resilience, we propose, develops in the first part of life as a response to adversity and early experience in general. This gives rise to a transgenerational pathway, distinct from social class trajectories. A theory of longevity inheritance should bring together previous thinking around general susceptibility, frailty and resilience with new insights from epigenetics and social epidemiology.

Highlights

• •Parents’ ages-at-death predict children's midlife and old-age mortality.
• •We speculate that these results reflect early programming of resilience.
• •Male resilience, measured at age 18, predicts mortality between ages 50 and 65.
• •Resilience is transmitted across generations, from fathers to sons.
• •Male descendants to long-lived parents are somewhat more resilient than their peers.

1. Introduction

Mortality, life expectancy and age-at-death are all strongly socially structured. Despite economic growth, welfare state provisions, modern medicine and a fundamental change in disease panorama, we find a negative social gradient in mortality generation after generation. We know from sociological studies that “the long shadow of the past” influences occupational and educational careers in successive generations, creating continuity in social (dis)advantage across generations. Because education, occupation and income all predict health and survival we should also expect such characteristics in the parental generation to predict the next generation’s health prospects, resulting in “inheritance of longevity”. It is possible, however, that this influence from previous generations is considerably broader than that working through the children’s own education, occupation and income. Variation in mortality risk within social groups is great. To understand “inheritance of longevity” we need a conceptual framework that also identifies those within-class influences.

Already in 1934 Kermack, McKendrick, and McKinlay (2001, reprinted) suggested that the first 15 years of life could determine your mortality risk during the entire lifecourse. Similarly, the so-called DOHaD (Developmental Origins of Health and Disease) theory suggests that early life experiences is an important determinant of adult health and disease (Gluckman, Hanson, Cooper, & Thornburg, 2008). DOHaD theory has focused on specific aetiologies and influences, such as that of foetal growth restriction on blood pressure and circulatory disease.

Another, earlier school of thinking, represented by epidemiologists Cassel (1974) and Syme and Berkman (1976) argued for more general disease-causing mechanisms. Demographers Vaupel, Manton, and Stallard (1979) noted the considerable individual heterogeneity in mortality risk. Concepts like frailty (Sternberg, Schwartz, Karunananthan, Bergman, & Clarfield, 2011; Vaupel et al., 1979), general susceptibility (Cassel, 1976, Syme and Berkman, 1976) or differential vulnerability (Nordahl et al., 2014) refer to individual differences in the ability to survive hardship. Cassel’s (1976) concept of host resistance forebodes the recent psychological discourse on resilience, defined as the capacity of a human being to “bounce back” in the face of adversity (Windle, 2011, Rutter, 2006). Weathering (Simons et al., 2016) and scarring (Heckman and Borjas, 1980, Stewart, 2001), are other related, but not identical, terms widely used in the economic literature to describe long-term change of individual characteristics in response to adversity.

Demographic concepts like frailty, epidemiological ones like general susceptibility and psychological ones like resilience all refer to the same real-life-phenomenon: a general rather than specific vulnerability to disease. Cassel (1976) and Syme and Berkman (1976) stressed its social roots, while Vaupel et al. (1979) perhaps assumed it to have a more genetic basis. Resilience, in turn, may be related to both views (Rutter, 2006). It could be thought of as the opposite extreme to susceptibility/frailty on the same underlying dimension. In this study, we argue that resilience is acquired early and maintained throughout life. Resilience should therefore influence the ability to survive up to a high age and be linked to longevity, as a number of studies indeed suggest (Shen and Zeng, 2010, Zeng and Shen, 2010, Charney, 2004).

“Inheritance of longevity” has been discussed at length in the literature. Its precise nature is somewhat elusive (Vaupel et al., 1998, Christensen et al., 2006, Pal and Tyler, 2016, Piraino et al., 2014). Gudmundsson et al. (2000), studying the entire Icelandic population, concluded that longevity was inherited within families, in their view probably because of shared genes. Hjelmborg et al. (2006), looking at twin data, concluded that genetic influences on the lifespan were minimal before age 60 and only increase after that age. Kowald and Kirkwood (2016), on the other hand, rejected any idea that mortality in old age is genetically programmed. Consistent with that view, a Swedish study of men born in 1913, found that a number of social and behavioural factors measured at age 50, but not their parents’ survival, predicted longevity (Wilhelmsen et al., 2011).

Evolutionary theorists have debated whether there is any evolutionary pressure to promote survival into old age (Williams, 1957). Nevertheless, we observe a steady lifespan extension in modern societies, especially among women, partly based on falling mortality rates across their long post-reproductive period. That children tend to live longer than their parents is likely to be determined both by what experience parents brings to the next generation, and by the improved life circumstances of the children themselves in their childhood and adult life. The importance of genetic factors for longevity, we suggest, may lie in their interaction with other factors, perhaps especially if this interaction takes place at an early age.

2. Theory

We make these theoretical proposals: The ability to survive into old age may be transmitted across generations. This inheritance cannot be reduced to the influence of parents’ social class or marital status at the time of the birth of the child or to the birth order of the new individual or to shared genes. In all social classes and family types there is considerable individual heterogeneity in the ability to reach a high age. We propose that this heterogeneity to some extent mirrors a person’s very early experience, such as her history of coping with challenging and adverse experience early in life. This would constitute a fundamental learning process, engaging the whole individual, mentally and physiologically, including the hypothalamus-pituitary-adrenal (HPA) axis, regulating neuroendocrine stress responses. How the individual handles early experiences, and whether or not she can rely on support from family and friends in this, may be crucial for the differential adaption to adversity. Small initial differences in trajectories between children in similar family circumstances, even between siblings, may be reinforced and greatly magnified during development, along a resilience/susceptibility dimension.

We may think of this process, determining resilience/susceptibility as a (potentially) adaptive “switch”, turned on early in life. The switch may involve epigenetic changes across large parts of the genome. If resilience is transmitted across generations, it would contribute to inheritance of longevity, beyond its link to social class. Three intergenerational pathways of resilience transmittance should be considered. Firstly, parental care and understanding how to cope with success and adversity (Meaney, 2001). Secondly, specific “longevity genes”, which promote resilience and a long life could be inherited in families (Gudmundsson et al., 2000). More intriguingly, thirdly, is the possibility that resilience may be fixed in the germline epigenome early in life as has been suggested by several researchers (Franklin et al., 2010, Vaiserman, 2012, Rando, 2016, Marsland, 2017, Sharma, 2017).

2.1. Aims of this study

Our theoretical ideas about longevity inheritance, and the role of resilience in this, led to a set of prior hypotheses, which we wanted to test. Thus, we examined length of lifespan and/or survival into old age in two consecutive generations: parents (G0) and their children (G1). In the next two generations, we compared fathers (G2) and sons (G3), with regard to a resilience measure, based on a psychological interview at military conscription at age 18. Finally, we explored the association between resilience and mortality, within and across generations.

We were able to address these questions empirically:

• 1)Does age-at-death of parents (G0) predict offspring’s (G1) mortality risk in midlife and old age?
• 2)If so, is this because parents (G0) who live longer also tend to promote a more advantageous social class trajectory for their children (G1)?
• 3)How do parents’ (G0) and their children’s (G1) lifespans compare?
• 4)Is resilience a characteristic which

• a)predicts later mortality (in G2)?
• b)is transmitted across generations (from G2 fathers to G3 sons)?
• c)is predicted by longevity in previous family generations (from G0 and G1 men and women to G2 and G3 men)?

3. Methods

3.1. Data material

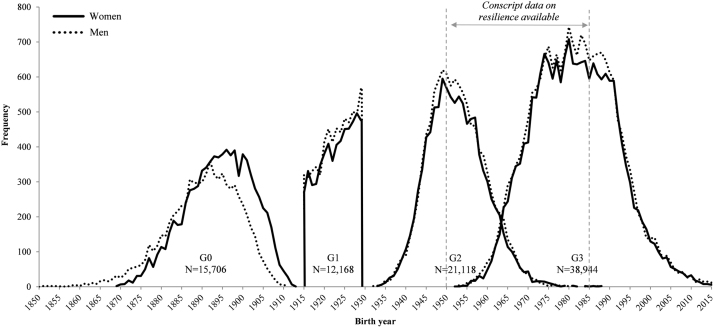
Four successive generations were linked by combining existing data on a cohort of all 14,193 men and women born alive at Uppsala Academic Hospital in 1915–1929 (Uppsala Birth Cohort Study: UBCoS) with information from Statistic Sweden’s Multigeneration Register through their personal identity numbers, to create UBCoS Multigen (Fig. 1). UBCoS individuals who were alive and resident in Sweden in 1947 (when PIN-numbers were introduced in Sweden) constitute generation 1 (G1: N = 12,168) in UBCoS Multigen (Fig. 2). This cohort and its successive generations have been extensively studied and presented previously (de Stavola, Leon, & Koupil, 2011; Fors, Modin, Koupil, & Vågerö, 2012; Juarez, Goodman, & Koupil, 2016; Modin 2002; Modin et al., 2008, Modin et al., 2009).

Fig. 1.

Birth year distribution of G0, G1, G2 and G3 by gender.

Fig. 2.

Overview of the process by which the final numbers of study subjects were selected for the analyses of G1 mortality.

We have now traced the parents of G1, with full names and birth date, through hospital records and parish registers. Members of this generation (G0: N = 15,706), are now dead; their date-of-death were traced through the Swedish Death Index (6th edition), published by Statistics Sweden and the Swedish Genealogical Society. This includes all recorded deaths in Sweden 1901–2013.

To increase comparability between G0 and G1, parenthood was an inclusion criterion also in G1. Details regarding inclusion of study subjects for analyses of G0 and G1 can be found in Fig. 2.

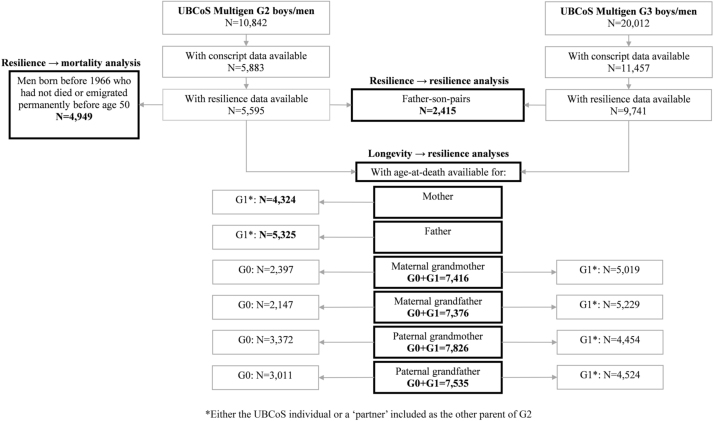
Fig. 3 defines the samples used for analyses of resilience as a determinant or as an outcome. G1 partners (the other parent to G2) were included in analysis of how longevity predict resilience in G2 and G3. See Modin et al. (2009) for a detailed description of inclusion of partners.

Fig. 3.

Overview of the process by which the final numbers of study subjects were selected for the analyses of G2 and G3 resilience.

3.2. Analyses and statistical methods

Mortality of G1 was analysed by tertiles of their parents’ (G0) age-at-death. G1 entered the at-risk-population November 1st 1960 or, if it occurred later, after their first childbirth. They were followed until death, the date of permanent emigration or the end of follow-up (December 31st 2015). Mother’s and father’s age-at-death, separately and in combination, were used to predict G1 mortality in mid- and later life. Parental social class and marital status were adjusted for in the analyses, as was G1’s birth order, birth year and adult social class. Estimates of G1 mortality risk before and after adjustments were compared to evaluate any mediation. Distributions of the independent variables can be found in Table 1.

Table 1.

Distribution of the independent variables used in the analysis of G0 and G1 (n = 9565).

	G1 men (n = 4871)		G1 women (n = 4694)
	n	%	n	%
G1 characteristics
Year of birth
1915–1919	1222	25	1165	25
1920–1924	1677	34	1579	34
1925–1929	1972	40	1950	42
Social class in 1960
Non-manual	1950	40	2196	47
Entrepreneur/farmer	2068	42	1645	35
Manual	720	15	699	15
Other	133	3	154	3
G0 characteristics
Mother’s maritalstatus at birth of G1
Married	3991	82	3750	80
Not married	880	18	944	20
Social class at birth of G1
Higher and intermediate non-manual	444	9	371	8
Entrepreneurs and farmers	871	18	800	17
Lower non-manual	340	7	278	6
Skilled manual	657	13	694	15
Unskilled manual	2137	44	2154	46
Other	422	9	397	9
Mother’s parity at birth of G1
1st	1932	40	1817	39
2nd	1147	24	1131	24
3rd–4th	1058	22	1032	22
5th–6th	393	8	382	8
7th or higher	341	7	332	7
Age-at-death (mothers)
Lowest third (16–73 years)	1630	33	1584	34
Intermediate third (74–84 years)	1678	34	1543	33
Highest third (85–105 years)	1453	30	1427	30
Unknown	110	2	140	3
Age-at-death (fathers)
Lowest third (21–69 years)	1474	30	1370	29
Intermediate third (70–80 years)	1360	28	1248	27
Highest third (81–106 years)	1404	29	1377	29
Unknown	633	13	699	15
Age-at-death (combined)
Both parents in youngest third	505	10	492	10
Intermediate	3271	67	3002	64
Both parents in oldest third	432	9	469	10
At least one parent unknown	663	14	731	16

G0 mid-parental age-at-death was compared with their G1 sons’ and daughters’ age-at-death in separate analyses of a segment of G1, those born 1915–1917, using linear regression techniques, adjusting for G1 birth year and birth order.

Further, G2 men’s mortality at ages 50–65 was regressed on their resilience scores, with and without control for their adult social class.

A regression coefficient was calculated for the association between G2 fathers’ and G3 sons’ resilience scores, controlling for G2 social class plus G2 and G3 conscription office.

Finally, we examined whether parental and grandparental longevity (in G0 and G1) predicts resilience in subsequent generations of young men (G2 and G3), adjusting for conscription office and parental social class.

Cox regressions with age as underlying time scale were used in analyses of G1 and G2 mortality. In all regressions, sibling-cluster robust standard errors based on shared mother or father were used to estimate 95% confidence intervals.

Statistical analyses were performed in Stata version 13.1.

3.3. Variables

3.3.1. Independent variables

Age-at-death (G0) was calculated from exact birth and death dates for the entire G0; then stratified by approximate tertiles, based on gender-specific age-at-death distributions (Table 1). Mother’s date-of-death was identified for 97% of G1 women and for 98% of G1 men. Father’s date-of-death, however, was missing for 15% and 13% of G1 women and G1 men respectively; in 94% of these cases G1 was born outside marriage. An additional category was constructed (“Unknown age-at-death”) to allow G1 women and men who were born out of wedlock to be properly represented in analyses. When combining mother’s and father’s age-at-death, four categories were used: both parents in the oldest third, both parents in the youngest third; an intermediate category of other combinations and finally those for whom at least one parent’s age-at-death was unknown.

Mid-parental age-at-death (G0) was calculated as father’s plus mother’s age-at-death divided by two, and used as a continuous variable in one of the analyses.

Longevity (G0 and G1) was defined as survival until at least age 85.

Birth year (G1) was grouped as 1915–19, 1920–24, 1925–29. Mother’s parity (G0) served as an indicator of G1 birth order and was grouped as 1; 2; 3–4; 5–6; 7+. Both factors were considered as potential confounders in analyses of G1 mortality.

Marital status (G0) was classified as: mother married or never married at the time of G1’s birth, excluding divorcees (n = 20) and widows (n = 57).

Social class (G0) at the time of G1 birth was based on father’s (G0) occupation when available; if not on mother’s (G0) occupation. It consists of six categories: higher and intermediate non-manuals, entrepreneurs and farmers, lower non-manuals, skilled manuals, unskilled manuals and other, following Modin (2002). The category of “house daughters” (unmarried non-working mothers who lived with their parents) was merged with non-classifiable into ‘other’.

Social class (G1) in 1960 was classified as manual, self-employed including farmers, or non-manual (Vågerö and Norell, 1989). It was considered as a potential mediator between G0 social class and marital status at G1 birth on the one hand and G1 mortality on the other.

Social class (G2) in adulthood was obtained from the 1980 or 1990 censuses, reclassified as manual workers, self-employed including farmers, or non-manual.

3.3.2. Dependent variables

All-cause mortality (G1) was followed-up until 2015 when the youngest members of G1 were 86 and the oldest 100 years old. G1 mortality was analysed as mortality before age 61 (“mid-life”), at 61–85 (“early old age”) and at 86–100 years (“old age”) for men and women separately.

Exact age-at-death (G1) was used as a continuous variable in a separate analysis of an almost entirely deceased segment of G1 born 1915–1917. Around 1% of these men (n = 7) and 2% of the women (n = 12) were alive at the end of follow-up, aged 98–100. For these we applied realistic annual death risks (0.33) year by year after 2015, to randomly assign a death year.

All-cause mortality (G2 men) was based on mortality at ages 50–65.

Resilience (G2 and G3 men) was based on semi-structured psychological interviews of all young men (age 18) at military conscription regarding their ability to resist severe psychological stress and to function in very adverse circumstances. Four different components were assessed, quantified and summarized as a nine step, normally distributed, ordinal scale, with a mean of 5.15 in both G2 and G3. The actual content and weight of the four components is kept confidential by military authorities. We used the summary score as a proxy for resilience/susceptibility, inspired by previous studies (Nilsson et al., 2001, Nilsson et al., 2004, Falkstedt et al., 2013). Lindqvist and Vestman (2011) gives a more detailed description of this measure.

Ethical permission was granted by Stockholm Regional Ethics Board (2015/904-31/5; 2016/933-32).

4. Results

4.1. Surviving to old age

For G1 men, both parents’ ages-at-death were independently associated with their mortality before age 61 and at ages 61–85, but not later in life. This also holds when parental social class and family marital status at G1 birth are controlled for. For G1 women, mothers’ age-at-death was associated with their own survival, across all observed ages, into very old age, also when parental social class and marital status at G1 birth are controlled for. Thus, G1 women with mothers in the highest third of age-at-death enjoyed a lower mortality risk before age 61, at 61–85 and at 86–100, independently of any influence from father’s age-at-death. The pathway from mother to daughter appears to confer a remarkably consistent intergenerational influence on mortality across the observed ages (Table 2, Table 3).

Table 2.

G1 men’s mortality by G0’s age-at-death: hazard ratios with 95% confidence limits based on Cox regression. Mortality follow-up 1961–2015 (n = 4871).

	Mortality before age 61 (543 deaths)			Mortality between ages 61–85 (2797 deaths)			Mortality between ages 86–100 (876 deaths)
	Models 1	Model 2	Model 3	Models 1	Model 2	Model 3	Models 1	Model 2	Model 3
Mother’s age-at-death
Youngest third	1.00	1.00		1.00	1.00		1.00	1.00
Intermediate third	0.99 (0.81, 1.21)	0.99 (0.81, 1.21)		0.96 (0.88, 1.05)	0.96 (0.88, 1.06)		1.08 (0.91, 1.28)	1.08 (0.91, 1.28)
Oldest third	0.75 (0.60, 0.94)	0.76 (0.61, 0.95)		0.77 (0.70, 0.85)	0.78 (0.70, 0.86)		0.96 (0.81, 1.14)	0.97 (0.82, 1.14)
(Unknown)	1.12 (0.65, 1.93)	0.97 (0.54, 1.72)		1.10 (0.85, 1.42)	0.97 (0.75, 1.27)		1.09 (0.72, 1.64)	1.11 (0.71, 1.74)
Father’s age-at-death
Youngest third	1.00	1.00		1.00	1.00		1.00	1.00
Intermediate third	0.87 (0.70, 1.08)	0.87 (0.70, 1.09)		0.94 (0.85, 1.04)	0.95 (0.86, 1.04)		1.14 (0.95, 1.36)	1.14 (0.95, 1.36)
Oldest third	0.79 (0.63, 0.98)	0.80 (0.64, 1.00)		0.82 (0.74, 0.90)	0.82 (0.74, 0.91)		1.02 (0.86, 1.22)	1.02 (0.85, 1.22)
(Unknown)	1.18 (0.90, 1.56)	0.91 (0.62, 1.33)		1.15 (1.02, 1.30)	1.06 (0.89, 1.27)		1.10 (0.86, 1.39)	0.88 (0.60, 1.30)
Both parents’ age-at-death
Both parents in youngest third	1.00		1.00	1.00		1.00	1.00		1.00
Intermediate	0.86 (0.65, 1.12)		0.86 (0.66, 1.13)	0.89 (0.78, 1.01)		0.89 (0.78, 1.01)	1.17 (0.93, 1.47)		1.17 (0.93, 1.47)
Both parents in oldest third	0.58 (0.38, 0.88)		0.59 (0.39, 0.90)	0.66 (0.55, 0.79)		0.66 (0.55, 0.80)	0.90 (0.66, 1.21)		0.90 (0.66, 1.21)
(At least one parent unknown)	1.16 (0.83, 1.63)		0.95 (0.63, 1.44)	1.09 (0.93, 1.28)		1.02 (0.84, 1.24)	1.17 (0.88, 1.56)		0.97 (0.65, 1.44)

Statistically significant estimates (95% CI) in bold type.

Models 1: Adjusted for G1 birth order and three bands of G1 birth years.

Models 2: Model 1 + parents’ social class and marital status at G1 birth and mutually adjusted.

Models 3: Model 1 + parents’ social class and marital status at G1 birth.

Table 3.

G1 women’s mortality by G0’s age-at-death: hazard ratios with 95% confidence limits based on Cox regression. Mortality follow-up 1961–2015 (n = 4694).

	Mortality before age 61 (295 deaths)			Mortality between ages 61–85 (2061 deaths)			Mortality between ages 86–100 (1166 deaths)
	Models 1	Model 2	Model 3	Models 1	Model 2	Model 3	Models 1	Model 2	Model 3
Mother’s age-at-death
Youngest third	1.00	1.00		1.00	1.00		1.00	1.00
Intermediate third	0.92 (0.71, 1.21)	0.92 (0.70, 1.20)		0.93 (0.83, 1.03)	0.92 (0.83, 1.03)		0.87 (0.75, 1.01)	0.87 (0.75, 1.01)
Oldest third	0.67 (0.49, 0.90)	0.68 (0.50, 0.91)		0.73 (0.65, 0.82)	0.74 (0.66, 0.82)		0.73 (0.63, 0.84)	0.73 (0.63, 0.84)
(Unknown)	0.71 (0.33, 1.53)	0.56 (0.26, 1.22)		0.83 (0.64, 1.08)	0.80 (0.61, 1.06)		0.92 (0.66, 1.28)	0.96 (0.69, 1.34)
Father’s age-at-death
Youngest third	1.00	1.00		1.00	1.00		1.00	1.00
Intermediate third	1.02 (0.74, 1.38)	1.00 (0.74, 1.37)		0.94 (0.84, 1.05)	0.94 (0.83, 1.05)		0.97 (0.83, 1.14)	0.98 (0.83, 1.15)
Oldest third	0.92 (0.67, 1.25)	0.92 (0.67, 1.26)		0.78 (0.69, 0.87)	0.78 (0.70, 0.88)		0.90 (0.77, 1.05)	0.91 (0.78, 1.07)
(Unknown)	1.47 (1.03, 2.11)	1.60 (0.96, 2.66)		0.97 (0.84, 1.11)	0.83 (0.68, 1.01)		0.96 (0.80, 1.17)	0.74 (0.56, 0.98)
Both parents’ age-at-death
Both parents in youngest third	1.00		1.00	1.00		1.00	1.00		1.00
Intermediate	0.85 (0.58, 1.24)		0.84 (0.58, 1.23)	0.77 (0.67, 0.88)		0.77 (0.67, 0.89)	0.90 (0.73, 1.10)		0.90 (0.73, 1.10)
Both parents in oldest third	0.83 (0.50, 1.39)		0.83 (0.49, 1.38)	0.59 (0.48, 0.72)		0.59 (0.48, 0.72)	0.72 (0.55, 0.94)		0.72 (0.56, 0.94)
(At least one parent unknown)	1.22 (0.78, 1.90)		1.16 (0.69, 1.95)	0.84 (0.71, 1.00)		0.74 (0.60, 0.92)	0.89 (0.70, 1.14)		0.72 (0.53, 0.97)

Statistically significant estimates (95% CI) in bold type. Models 1: Adjusted for G1 birth order and three bands of G1 birth years. Models 2: Model 1 + parents’ social class and marital status at G1 birth and mutually adjusted.

Models 3: Model 1 + parents’ social class and marital status at G1 birth.

Having two parents with high ages-at-death gave an even stronger gradient; for G1 men a distinctly reduced mortality risk at age 61–85 (HR = 0.66), and particularly before age 61 (HR = 0.59); for G1 women we observed HRs of 0.59 at ages 61–85 and of 0.72 at ages 86–100 years (Table 2, Table 3).

Estimates of G1 mortality by G0 age-at-death were minimally influenced by controlling for G0 or G1 social class (results available on request). In that sense, G0 age-at-death is a distinct predictor of G1 mortality. It appears to represent a different pathway from that of early or adult social class. In fact, parents’ ages-at-death appear to be more consistent predictors of G1 men’s and women’s mortality than is their social trajectory.

Analyses of a segment of G1 (those born 1915–1917) showed that G1 tend to live longer than their G0 parents in all social classes and in both marital status groups. Median difference in age-at-death, comparing G1 men and their fathers, was + 3.9 years; when comparing G1 daughters to their mothers it was + 6.9 years (data not shown). The age-at-death distribution has thus shifted to the right when G0 and G1 are compared. Variation in age-at-death has also fallen. Standard deviations around mean age-at-death for G0 women are 16.5 years and for their G1 daughters 12.6 years, whereas for G0 men and their sons the corresponding figures are 14.3 and 12.7 (data not shown).

The secular trend of falling variation in age-at-death is known from the literature (Smits and Monden, 2009) and often explained by falling infant and child mortality rates. Here, however, it is based on falling adult mortality rates, since all individuals in G0 and G1 have survived childhood long enough to become parents.

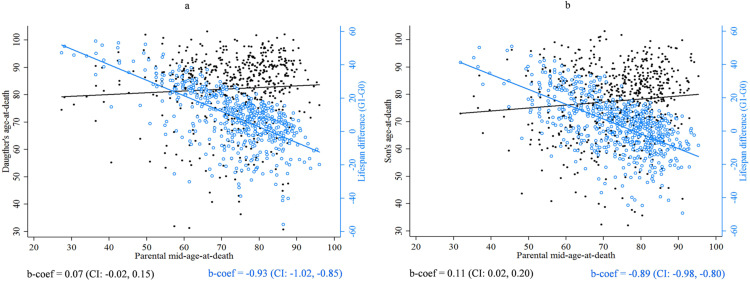
Regressing the exact age-at-death of (G1) sons and daughters on (G0) mid-parental age-at-death (Fig. 4) gives modest regression coefficients with wide confidence limits of b = 0.11 (95% CI 0.02, 0.20) for sons, and 0.07 (CI -0.02, 0.15) for daughters.

Fig. 4.

a-b. Age-at-death for G1 daughters (a; n = 529) and G1 sons (b; n = 620) by their parents´ mid-age-at-death indicated by dots. G1–G0 difference in lifespan in years, indicated by circles. Regression lines, b-coefficients and 95% confidence limits. Based on G1 born 1915–17.

Offspring age-at-death varies considerably around parental age-at-death. Many other factors, beyond their parents’ longevity and social class, influence longevity in the next generation. The phenomenon of “regression to the mean”, observed by Galton (1886) already, indicates that a number of unobserved determinants, and their combinations, including chance, are at play. They operate in such a way that the discriminatory accuracy of mid-parental age-at-death is low. Your parents’ age-at-death (or most other determinants) can therefore be a rather poor predictor of your own age-at-death, even if there is a causal link.

Fig. 4a and b show the G1–G0 difference by G0 age-at-death: a steep negative regression line (in both graphs b = − 0.9; p < 0.001). Thus, children of parents who lived relatively short lives enjoyed a much larger increase in lifespan compared to their parents than did others. As a low attained age is partly due to randomly distributed causes, we would expect a “regression to the mean” at both ends of the age-at-death distribution; the steeper the smaller the role of inheritance. We do indeed observe a strong regression to the mean, suggesting that (genetic or non-genetic) inheritance plays a modest role.

4.2. Resilience analyses

We explored inheritance of resilience. Linear regression reveals an association between G2 fathers and G3 sons in resilience scores, controlling for G2 adult social class (b = 0.21, 95% CI = 0.17, 0.25) (data not shown). It seems likely that resilience is also correlated between G0 and G1, beyond its link to social class.

Regressing G2 all-cause mortality at ages 50–65 on G2 resilience scores, controlling for G2 adult social class, gave a hazard ratio of 0.92 (95% CI 0.84, 0.99) per unit (Table 4) In fact, social class and resilience were both independent predictors of mortality (not shown). Thus, a large part of the mortality variation across resilience scores takes place within social classes. Excess mortality for the lowest resilience group can be calculated to be 2.02 (95% CI = 1.06, 3.86) compared to the highest. Looking closer suggests mortality to be a curvilinear function of resilience, with a disproportionately high mortality burden in the two lowest resilience groups.

Table 4.

G2 men’s mortality at ages 50–65 by a 1 step increase of their resilience score at age 18: hazard ratios with 95% confidence limits based on Cox regression. Mortality follow-up 2000–2015 (n = 4949).

	Mortality at ages 50–65 (193 deaths)
	Model 1	Model 2
Resilience score at age 18	0.90 (0.83, 0.98)	0.92 (0.84, 0.99)

Statistically significant estimates (95% CI) in bold type.

Model 1: Adjusted for four bands of birth years and conscription office. Model 2: Model 1 + social class at age 25–34.

In addition, our results suggest that both mothers’ and fathers’ longevity (surviving to age 85) is associated with resilience in their male offspring. Intriguingly, the longevity of maternal grandmothers, but not of any of the grandfathers, is associated with their grandsons’ resilience scores (Table 5).

Table 5.

G2 and G3 men’s resilience score according to their parents and grandparents’ survival to age 85: b-coefficients with 95% confidence limits based on linear regression.

		G2 and G3 men’s resilience scores at age 18
Longevity (≥ 85 years)	%b	Model 1	Model 2	nc
Mothera	56	0.27 ( 0.14, 0.39)	0.22 (0.10, 0.35)	4324
Fathera	36	0.23 ( 0.11, 0.34)	0.16 (0.04, 0.27)	5325
Maternal grandmothera	46	0.14 ( 0.05, 0.23)	0.13 (0.04, 0.22)	7416
Maternal grandfathera	30	0.02 (− 0.08, 0.11)	0.00 (− 0.09, 0.10)	7376
Paternal grandmothera	45	0.10 ( 0.01, 0.19)	0.08 (− 0.01, 0.16)	7826
Paternal grandfathera	27	0.03 (− 0.07, 0.13)	0.01 (− 0.09, 0.11)	7535

Statistically significant estimates (95% CI) in bold type.

Model 1: Adjusted for conscription office.

Model 2: Model 1 + parent’s social class at age 31–61 (G1) or 25–34 (G2).

^aReference category: did not survive to age 85.

^bProportion of parents/grandparents who survived to age 85.

^cNumber of G2 and/or G3 men in the analysis.

Thus, resilience and long-term mortality are linked within a generation; for both there is a continuity across generations. Finally, longevity in the previous generation(s) is linked to resilience in their (male) offspring. All this suggests that resilience could play some role in the inheritance of longevity.

5. Discussion

5.1. Strength and limitations

This study of UBCoS Multigen covers four generations and presents G0 lifespan data for the first time. The parents (G0) of the first generation, G1, are all dead. The use of G0 age-at-death as a predictor for events in later generations is a unique feature of this study. G0 were identified from G1 births 1915–29, but our analyses do not cover G0’s children born outside that period. In some of the analyses, we used only a segment of G1, those born 1915–1917, giving rather low statistical power.

Parents are a healthy subset of all individuals and they tend to live longer than childless women and men (Hurt, Ronsmans, & Thomas, 2006). To increase comparability between generations (G0 and G1), we restricted our analyses to those individuals in G1 who were themselves parents.

Data about resilience scores at age 18 were available for males in G2 and G3. This is a limitation, particularly because it excludes women. However, the observed associations in resilience could well be similar for women and for the two previous generations.

We calculate estimates of average causal effects in a population, or in segments of a population. These are useful when considering “causes of population incidence” (Rose, 1985) or differences between groups. They are less useful as predictors of individual events of disease or death (Merlo, Mulinari, Wemrell, Subramanian, & Hedblad, 2017), since individual responses to risk factors show a very large variation, which is only covered marginally by our analyses here.

Having information for four linked generations is the unique strength of this study. Even though the available information is not identical for each generation, it provides an opportunity to better understand the nature of parent-offspring associations in achieving a high age.

Below, we discuss possible pathways of longevity inheritance in the light of our proposals in the previous theory section.

5.2. Social and genetic pathways

We lack behavioural and genetic data; this leaves many questions about the pathways and inheritance of longevity unanswered. Familial clustering of longevity could suggest a genetic pathway. Hjelmborg et al. (2006), however, found genetic influences to be less important for mortality before age 60 and to increase with rising age. We found that 1) parents’ age-at-death is associated with mortality in G1 men and women both before and after age 60 and 2) no tendency at all for the association between G0 age-at-death and G1 mortality to increase with age. It is therefore likely to reflect a different kind of inheritance. Kowald and Kirkwood (2016) recently dismissed any possibility of aging being genetically programmed. The strong variation in G1 age-at-death around a specific value for G0 age-at-death (Fig. 4) gives some support for their view. Any direct genetic influence is probably rather small. Pal and Tyler (2016) suggested that, rather than being genetically determined, lifespans are epigenetically determined, based on genome-wide responses to external events, during both development and aging.

Wilhelmsen et al. (2011) found that parents’ survival had no influence on their sons’ survival up to age 90. A possible explanation for the difference compared to the present study is that they measured parental survival by whether the parent was dead or alive when the son was 50 years old, ignoring later deaths and parental survival to more advanced ages. However, they did find a number of social and behavioural factors at age 50, such as smoking and a high coffee consumption, which predicted death before age 90 among the men. Both these behaviours may be considered ways of coping with stress and hardship, developed earlier in life.

G1 men and women born 1915–1917 had longer lifespans than their parents; daughters, especially, lived longer than their mothers. Female emancipation and social change during the 20th century has been accompanied by a stronger reduction in mortality among women than among men (Hemström, 1998). Hemström used the term “male susceptibility” to explain the difference between male and female long-term mortality trends. This was a reference to male risk-taking behaviour, developed as a particular, non-healthy way of coping with adversity in modern society.

Zeng and Shen found resilience to hardship as well as social friendships to be important for longevity (Zeng and Shen, 2010, Shen and Zeng, 2010). Their emphasis on social support as an aspect of resilience resembles the way Cassel (1974) and Syme and Berkman (1976) originally conceived of general susceptibility. A relatively short lifespan could be considered the result of an underlying frailty or general susceptibility. In contrast, we can think about individuals who live long lives as being particularly resilient, able to cope with adversity at any age.

5.3. Resilience as a possible mechanism in the intergenerational transmission of longevity

According to Windle’s (2011) systematic review of the literature, resilience is used in many different contexts and with a variety of definitions. The core of the concept seems to be the personal capacity to “bounce back” in the face of adversity. Resilience may be developed early in life as a successful response to adversity (Garmezy, 1993, Phillips et al., 2016). Repeated adversity is often linked to early social class, a marginal social position or lack of family resources, pointing to the importance of the social and material context. Repeated adversity, followed by repeated successful responses, should constitute a dynamic learning process. This process must be influenced both by luck and by cross-talk between genes and experience, finally resulting in a high degree of resilience. Escaping “the long shadow of the past”, in fact. Alternatively, if repeated adversity is followed by repeated failure to cope, we may instead see the gradual emergence of a “general susceptibility”, crucially linked to the social environment, as Cassel suggested in 1976.

Early experience of adversity may thus be seen as a switch between the alternative paths of resilience and susceptibility, pressed relatively early in life. Hertzman and Boyce (2010) wrote in similar terms that “early experiences can produce small changes in trajectories, which can become magnified as individuals develop” (page 334).

In our study, resilience was identified at military conscription by a trained psychologist through a semi-structured interview. The interview covered past adjustment problems; conflicts and successes; responsibilities and initiatives taken at school, at home, at work and in leisure time. Mental energy, social maturity and stability were assessed. How a person would handle situations of severe stress in the future was assessed (with scores 1–9) against the background of his previous history. This is a strength of the present study.

We found a continuity of resilience from fathers to sons, independent of parental social class. Transmission of this characteristic across generations could happen through several mechanisms (not mutually exclusive), such as learning from parents or transmission of specific genes. Of theoretical importance is the hypothesis that early experience can also cause epigenetic modification of germ-line DNA and potentially influence gene expression and longevity in the next generation (Franklin et al., 2010, Vaiserman, 2012, Rando, 2016, Marsland, 2017, Sharma, 2017).

5.4. Biological programming, epigenetics and social epidemiology

Barker, Forsen, Uutela, Osmond, and Eriksson (2001) suggested that optimal foetal growth created resilience to the health consequences (such as heart disease mortality) of poor living conditions. We believe that their focus was too narrow and suggest that human resilience is shaped over a much longer period which includes childhood and adolescence. Barker’s concept of foetal programming has now been replaced by that of developmental programming. Interaction between genetic potential and early experience causes epigenetic changes during development.

Simpkin et al. (2017) found a number of developmental features to be linked to methylation patterns at birth and at age 7. They discussed whether epigenetic age should be seen as an aggregate measure of maturity in childhood. However, they cautioned against this, since they found it to be unrelated to the onset of puberty. Indeed, if individual response to early experience affects the way children develop (becoming resilient rather than susceptible, for instance), it would seem wrong to conceptualise this as a feature of maturity or epigenetic aging. Beach, Lei, Brody, Kim, Barton, and Dogan (2016) called for an investigation into “SES risk exposure and protective factors that occur during pre-adolescence or later and that may be mediated by epigenetic change”. They found that “a supportive family at age 10–13 is associated with epigenetic pattern at age 19”.

Thus, there is at least theoretical support for the idea that resilience/susceptibility in humans is epigenetically programmed early in life. This makes our measure of resilience at age 18 appropriate for studying the role of resilience in the inheritance of longevity. We found that the longevity of both parents (surviving to age 85) was associated with resilience in their male offspring. This is a parallel to Horvath et al. (2015), who reported that adult offspring of long-lived persons had a particularly low epigenetic age. Miller and colleagues, in turn, linked epigenetic age to resilience and self-control among young adults (Miller and Chen, 2013, Miller et al., 2015).

Among adult humans, epigenetic changes of the genome are robust markers of biological age (Chen et al., 2016). Epigenetic age among adults predicts longevity independently of chronological age, even after adjusting for known risk factors. This suggests the intriguing possibility that epigenetic age (epigenetic age advancement) measured in adulthood or in old age, but not in childhood, is a correlate to general susceptibility/resilience at genome level. Whether resilience, in fact, is related to epigenetic age among adults, is a challenging research question.

The transmission of resilience across generations is a further question. If resilience is acquired in the parental generation, it could be transmitted to the next generation, either through an epigenetic pathway or through learning from parents, or through a combination of both. We found that both mothers’ and fathers’ longevity was associated with resilience in the following generation, consistent with both pathways. Genetic variants favouring brain plasticity could probably amplify the “switch” between susceptibility and resilience. Belsky and Beaver (2011) showed that “cumulative-genetic plasticity” interacts with parenting to shape adolescent self-regulation. The negative effects of poor parenting and the positive effects of good parenting were stronger among those with more plasticity.

The fact that the longevity of maternal grandmothers (but not any of the grandfathers) was associated with resilience in grandsons, is also compatible with the “grandmother hypothesis”, which postulates that grandmothers, in particular, invest in their grandchildren’s future. A review by Strassman and Garrard (2011) found this “to hold only for the maternal and not the paternal grandmother”.

6. Conclusion

We conclude that parents’ longevity predicts their children’s long term mortality. This influence is modest but robust, not confounded by the social class and marital status of their parents at their birth, and distinct from their own social class trajectories. Kowald and Kirkwood (2016) posed the question of whether aging is genetically programmed. Their answer was no. We suggest that early “programming” of resilience, epigenetically and culturally transmissible across generations, is a more likely hypothesis. Individual resilience, we propose, is developed in the first part of life as a response to adversity and early experience in general. This is in line with recent animal research which has shown that early life stress encodes lifelong susceptibility to stress via long-lasting transcriptional programming (Peña et al., 2017). Our finding that men with the lowest resilience scores disproportionally suffer midlife mortality is not surprising.

Risk factors, and social determinants of health, work on populations with considerable individual variation. Understanding longevity inheritance therefore calls for new ideas. A theory of longevity inheritance should bring together previous thinking around general susceptibility, frailty and resilience with new insights from epigenetics and social epidemiology.