Algorithm-driven optimization of cryopreservation protocols for transfusion model cell types including Jurkat cells and mesenchymal stem cells

Abstract

This investigation describes the use of a differential evolution (DE) algorithm to optimize cryopreservation solution compositions and cooling rates for specific cell types. Jurkat cells (a lymphocyte model cell type) and mesenchymal stem cells (MSCs) were combined with non-DMSO solutions at concentrations dictated by a DE algorithm. The cells were then frozen in 96-well plates at DE algorithm-dictated cooling rates in the range 0.5–10°C/min. The DE algorithm was iterated until convergence resulted in identification of an optimum solution composition and cooling rate, which occurred within six to nine generations (seven to 10 experiments) for both cell types. The optimal composition for cryopreserving Jurkat cells included 300 mM trehalose, 10% glycerol and 0.01% ectoine (TGE) at 10°C/min. The optimal composition for cryopreserving MSCs included 300 mM ethylene glycol, 1 mM taurine and 1% ectoine (SEGA) at 1°C/min. High-throughput concentration studies verified the optimum identified by the DE algorithm. Vial freezing experiments showed that experimental solutions of TGE at 10°C/min resulted in significantly higher viability for Jurkat cells than DMSO at 1°C/min, while experimental solutions of SEGA at 10°C/min resulted in significantly higher recovery for MSCs than DMSO at 1°C/min; these results were solution- and cell type-specific. Implementation of the DE algorithm permits optimization of multicomponent freezing solutions in a rational, accelerated fashion. This technique can be applied to optimize freezing conditions, which vary by cell type, with significantly fewer experiments than traditional methods.

1. Introduction

Over 1 million patients have been treated with stem-cell derived therapies, and the economic impact of stem-cell derived therapies has grown to > $1 billion/year (Mason et al., 2011), with annual growth rates on the order of 15–20%. Cells used therapeutically are typically collected in one location, processed in a second location and administered in a third. In addition, the ability to preserve cells enables coordination between manufacture of the product and patient treatment regimes. The critical biological properties of the cells must be preserved in order for this type of therapy to be effective.

Conventional methods of cryopreserving cells since the 1970s have involved the use of dimethyl sulfoxide (DMSO). However, DMSO is systemically toxic in humans and can result in side-effects ranging from mild (such as nausea and vomiting) to severe (including cardiovascular and respiratory complications) when transfused in even trace amounts with thawed cells (Windrum et al., 2005). Additionally, DMSO increases the mRNA level of the de novo DNA methyltransferase Dnmt3a, accompanied by hyper- or hypomethylation of many genetic loci (Iwatani et al., 2006), making it unsuitable for use with reprogrammed cells of high therapeutic value, such as induced pluripotent stem cells or cells derived from them.

Recent studies suggest that certain cell types used therapeutically exhibit altered/diminished in vitro post-thaw function (Pollock et al., 2015). Mesenchymal stem cells have demonstrated diminished indolamine deoxygenase activity (Francois et al., 2012) and altered cytoskeletal function (Chinnadurai et al., 2014) after thawing. It has been hypothesized that these alterations in post-thaw function resulted in the failure of a recent clinical trial using cryopreserved MSCs (Francois et al., 2012). Other studies have demonstrated that natural killer cells used for immunotherapies may also exhibit diminished post-thaw function (Mata et al., 2014). Clearly, the development of alternative methods of preserving cells to eliminate DMSO and improve post-thaw function is desirable.

Survival for many cell types is strongly influenced by cooling rate, with a narrow range of cooling rates over which post-thaw survival is optimal (Leibo and Mazur, 1971). Freezing solution composition also influences cell survival (Mazur, 1984), and changing the composition of the cryopreservation solution may change the cooling rate at which optimum survival is observed. Cryopreservation protocols are most often determined empirically by changing the composition and cooling rate until the desired outcome is obtained (Conrad et al., 2000; Dijkstra-Tiekstra et al., 2014; Dong et al., 2009; Freimark et al., 2011; Kearney et al., 1990). This process is typically expensive, time-consuming and may not result in an optimized protocol.

A variety of strategies can be used to optimize processes with multiple inputs (composition of the freezing solution and cooling rate) and outputs (recovery and viability). The objective of this investigation was to describe the use of the differential evolution (DE) algorithm (Storn and Price, 1997) to optimize compositions and cooling rates for cryopreservation solutions. Other investigators have successfully used DE for other applications, including Tsutsui et al. (2011), who used this approach to optimize the formulation of embryonic stem cell media. In the experiments described here, DE is applied for the purpose of determining DMSO-free cryopreservation solution formulations for different cell types (lymphoblasts and mesenchymal stem cells). The approach was also used to optimize the solution composition and cooling rate simultaneously. The methods involved have been adapted to a high-throughput format: small numbers of cells are used and a small number of experiments are required for optimization. This type of approach will transform the development and optimization of freezing protocols by reducing the number of cells and experiments required, thus accelerating optimization over a multiparameter space.

2. Materials and methods

2.1. Cell culture

The lymphoblastoid cells used in this study (Jurkat cells; ATCC TIB-1522) were cultured in medium composed of high-glucose RPMI 1640 (Life Technologies, Carlsbad, CA, USA) and 10% fetal bovine serum (FBS; Qualified, Life Technologies, Carlsbad, CA, USA). Jurkat cells were cultured to maintain cell density within 1 × 10⁵–3 × 10⁶ cells/ml.

The mesenchymal stem cells (MSCs) used in this study were derived from H9 embryonic stem cells, as previously described (Trivedi and Hematti, 2008). MSC medium was composed of αMEM base with glutamine powder (Life Technologies), 10% FBS (Qualified) and 1% non-essential amino acids (Life Technologies). Tissue-culture flasks were coated with 0.1% porcine gelatin (Sigma-Aldrich, St. Louis, MO, USA) for a minimum of 2 h before cell seeding. MSCs were seeded in gelatin-coated flasks at a density of ca. 2500 cells/cm². Cells were split or used for experiments when they reached approximately 70–80% confluence and were used for experiments at passages 8–12 only.

2.2. Algorithm

The DE algorithm used in this study was developed from strategy 2 (DE/local-to-best/1, which balances robustness and convergence) by Storn and Price (1997) and was coded in MATLAB by modifying existing open source Storn and Price MATLAB code to accept discrete parameters, and output information about the test population and emergent population after each iteration. The DE algorithm utilizes stochastic direct search and independently perturbs population vectors to identify a global maximum within the user-defined parameter space. Briefly, the DE algorithm randomly generates an initial population (generation 0) that spans the entire parameter space. This population is composed of a given number of solutions expressed as vectors (a set of numbers), and the number of different solution components being tested defines how many slots the population vectors have. Experimentally, these vectors correspond either to the different levels of solute in a solution or to different cooling rates (Table 1). Cells are frozen at DE algorithm-dictated cooling rates with solutions made from these vector specifications, and the resulting experimental live cell recoveries are iterated back into the DE algorithm.

Table 1.

Discrete concentration levels and cooling rates used for each component in the DE algorithm

	Level 0	Level 1	Level 2	Level 3	Level 4	Level 5
Component	(0)	(1/100)	(1/50)	(1/10)	(1/2)	(1)
Trehalose (mM)	0	3	6	30	150	300
Glycerol (%)	0	0.1	0.2	1	5	10
Ectoine (%)	0	0.01	0.02	0.1	0.5	1
Sucrose (mM)	0	3	6	30	150	300
Ethylene glycol (mM)	0	3	6	30	150	300
Alanine (mM)	0	3	6	30	150	300
Taurine (mM)	0	0.5	1	5	25	50
Cooling rate (different scaling) (°C/min)	0	0.5	1	3	5	10
DMSO standard recovery ± standard deviation. (for cooling rates in same column above)	0	0.09 ± 0.03	0.13 ± 0.03	0.12 ± 0.04	0.12 ± 0.04	0.09 ± 0.01

The DE algorithm utilizes this experimental information to modify the existing population vectors, and predicts solutions that may result in more favourable live cell recovery. Briefly, the algorithm mutates existing vectors to generate new test vectors, and performs head-to-head comparisons of the resulting experimental live cell recovery of each of the population slots. The best value from this comparison (either the original or the new mutant vector) is stored in an emergent population. This mutation/comparison process is repeated for all subsequent generations (Figure 1) and results an emergent population that changes less and less as the algorithm converges. The final emergent population contains set of solutions that have all been independently optimized using stochastic direct search, and contains the best possible compositions for freezing cells within the defined parameter space. Convergence can be measured by observing an increase in cumulative best member live cell recovery, a decrease in the number of improved solutions within the emergent population after each generation, or by the generational average, which captures both these metrics.

Figure 1.

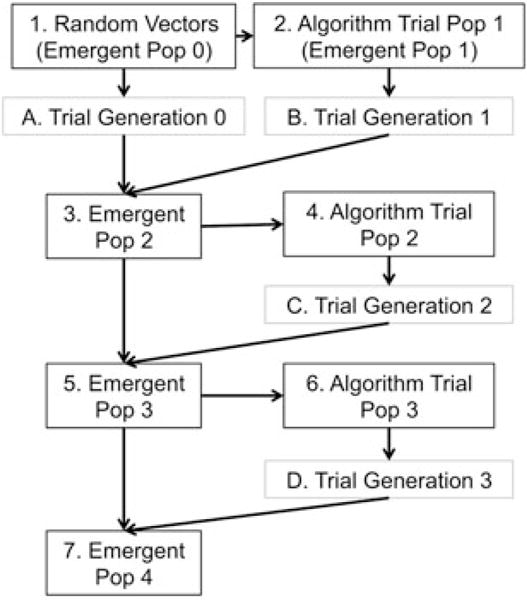
DE algorithm flow chart, with black boxes representing DE algorithm steps and grey boxes representing experimental steps. The DE algorithm produces a population in gen 0 that randomly spans the parameter space, and a trial population (gen 1) that is based on mutation of gen 0. These are both experimentally tested by the user and the live cell recovery results are input into the DE algorithm, producing an emergent population which is further mutated and iterated in subsequent experiments. As the algorithm converges, an optimum solution can be identified

For these experiments, the generation size was set to either 18 or 27, the crossover set to 1 and the weight set to 0.85. The concentration of each component was allowed to vary discretely between 0 and the maxima that were identified from the literature or dictated by solubility limits. The concentrations used for each discrete level are listed in Table 1.

2.3. High-throughput 96-well plate freezing

In both screening and DE algorithm experiments, cells were frozen in 96-well plates to limit the number of cells and volumes of reagent necessary, and to increase the number of samples that could be tested at one time. Solutions were made at 2× their final concentration in distilled water (diH₂O). Cells were centrifuged and supernatant was aspirated before cells were suspended in Normasol-R™. Cells were combined 1:1 with 2× solutions, using a single-step addition in clear-bottomed black 96-well plates (Corning, NY, USA) to produce a 1× concentration of cryoprotectant solution with a total volume of 50 μl and a cell concentration of ca. 300, 000 cells/well (~6 million cells/ml). Actual seeding counts were confirmed by manual acridine orange/propidium iodide (AO/PI) counts of the cell stock added to each plate. As a control, wells of 10% DMSO solution were also included on each plate to normalize results between all experiments. All samples were run in triplicate wells on each plate. The plates were sealed with molded silicone round well covers (Laboratory Supply Distributers, Millville, NJ, USA) to prevent desiccation during freezing and storage. The plates were placed in a rack in a controlled-rate freezer, and frozen using the profile below:

1. Starting temperature 20°C

2. −10°C/min to 0°C

3. Hold at 0°C for 15 min

4. −1°C/min to −8°C

5. −50°C/min to −45°C

6. +15°C/min to −12°C

7. −0.5, −1, −3, −5 or −10°C/min to −100°C (as dictated by the DE algorithm)

The rapid cooling and rewarming in steps 5 and 6 are included to promote ice crystal nucleation outside the cell before slow cooling proceeds, discouraging stochastic ice formation within the cells. A temperature of −8°C was selected for this step, as a conservative temperature at which all possible solution compositions should have exceeded their freezing point (based on their predicted osmolarity) to ensure that this ice nucleation step would be successful.

2.4. Vial freezing

Freezing of cells in vials was performed to compare the post-thaw recovery obtained in 96-well plates (50 μl) to that observed in conventional cryovials (1 ml). Briefly, solutions were prepared at 2× the final freezing concentration and added stepwise to cells in Normasol-R™ at a 1:1 final volume ratio in a 1.8 ml Nalgene™ CryoTube vial (Nunc, Thermo Scientific, Waltham, MA, USA). Vials were moved to the controlled-rate freezer immediately and were frozen using the same protocol as for 96-well plates.

2.5. Thawing

Both 96-well plate and vial samples were thawed using a 37°C water bath. Vials were submerged in a 37°C bath (to just under cap level) and agitated until only a small ice crystal was present.

Plates were also thawed using a 37°C water bath. Briefly, the plates were submerged to half their height and agitated for 1 min. At t = 1 min, they were removed from the bath and the silicone cover was removed to observe the samples as they thawed. The plates were returned to the 37°C water bath and again submerged to half their height. When opaque samples became transparent (ca. 1 min after being returned to the water bath) the plates were removed for immediate addition of viability dye. Thermocouple probe analysis of the freezing and thawing rate in different wells of a 96-well plate showed that no significant difference existed in the temperature profiles of the wells tested in the experiments.

2.6. Viability assessment

The viability of all cells was assessed before freezing using fluorescent acridine orange/propidium iodide (AO/PI), using the method described in more detail in Pollock et al. (2015). Briefly, AO/PI was added to cell samples and live and dead cells were enumerated using a haemocytometer (minimum of 200 cells counted). This method was also used to measure the viability and live cell recovery of vial samples immediately after thawing. Viability was determined by dividing the number of live cells by the number of total cells. Live cell recovery was determined by dividing the number of live cells post-thaw by the number of live cells seeded pre-freeze. All dilutions were accounted for in the calculation of both viability and live cell recovery. All future instances of recovery in the text refer to live cell recovery, not total cell recovery.

After the 96-well plates were thawed, a dye composed of calcein AM (ex/em = 494/520 nm) and PI (ex/em = 535/617 nm) was added to each well and the wells were covered against light and placed in a 37°C incubator for 30 min to allow the live cells to cleave calcein AM; the latter was used for these experiments instead of acridine orange (which has multiple fluorescent peaks, one of which overlaps with the peak for propidium iodide), as it has narrow excitation/emission peaks that do not interfere with the peaks for propidium iodide. The plates were then analysed for fluorescence on a plate reader, using existing filter sets with excitation/emission wavelengths of 485/528 nm to measure calcein fluorescence and 530/590 nm to measure PI fluorescence. Raw fluorescence values were used to calculate the number of live and dead cells present in each well, by correlating to a control curve of unfrozen cells generated using serial dilution of known live and dead (killed using heat shock at 60°C for 15 min) cell counts. The live cell recovery was calculated by dividing the number of live cells present in thawed samples (calcein AM plate reader fluorescence) by the number of live cells seeded pre-freeze (AO/PI counts visually observed on a haemocytometer for the seeded cell stock). To normalize results between different plates and different cooling rates, these raw recoveries were divided by a control well containing 10% DMSO on the same plate (to normalize for stochastic variations in freezing experienced by the plate as a whole), then multiplied by a standard DMSO recovery at each cooling rate to give the ‘scaled raw recovery’. After each experimental generation, the DMSO recovery for each cooling rate was averaged with all DMSO recoveries at that cooling rate from previous generations to calculate the DMSO standard recovery for that cooling rate, and the scaled recovery for all data from all generations was recalculated at the conclusion of each generation, based on these new standards, before reiteration through the algorithm. The final DMSO standard recoveries for Jurkat cells at each cooling rate are listed in Table 1. The differences in DMSO recovery between cooling rates were noticeable and, although not statistically significantly different, they consistently fell in the same order relative to one another at each generation, which is why simply scaling to the DMSO recovery on each plate without correcting for the cooling rate would give an incomplete picture of each experimental recovery.

Example calculation:

$$\frac{\text{Raw recovery}}{\text{DMSO plate recovery}}\ast \text{DMSO standard recovery}=\frac{0.2}{0.15}\ast 0.16=0.21=\text{scaled raw}\text{recovery}$$

2.7. Statistics

Error bars represent standard deviations (SDs) of a minimum of nine sample measurements, taken from experiments performed in batches of three to six over a minimum of 3 different days. Statistical significance was determined using Student’s t-test, with a significance level of p = 0.05.

3. Results

3.1. Optimizing a solution composition for a given cooling rate

The first phase of this study involved using the DE algorithm to optimize a three-component cryopreservation solution used at a single cooling rate (1°C/min). Three components, trehalose, glycerol and ectoine (TGE), were selected to comprise the freezing medium used for the preservation of Jurkat cells (a haematopoietic model cell type) based on prescreening of multiple non-DMSO components. For this single cooling-rate study, the DE algorithm was programmed to output 18 vector solutions/generation, with weight = 0.85 and crossover =1. Jurkat cells cryopreserved in 10% DMSO at a cooling rate of 1°C/min were used as a control.

For each generation of solutions tested, the scaled raw recovery of the best solution increased or remained constant (Figure 2A), while the number of solutions that demonstrated improved recovery tended to decrease for each generation (Figure 2B). These results together (Figure 2C) indicate that the DE algorithm converged after six generations (e.g. seven freezing experiments) to an optimum solution composition of 150 mM trehalose, 10% glycerol and 0.1% TGE (Figure 2). The recovery of Jurkat cells frozen in the TGE solution was 32%, almost twice as high as the recovery of the control (16% = highest observed recovery in 10% DMSO at 1°C/min).

Figure 2.

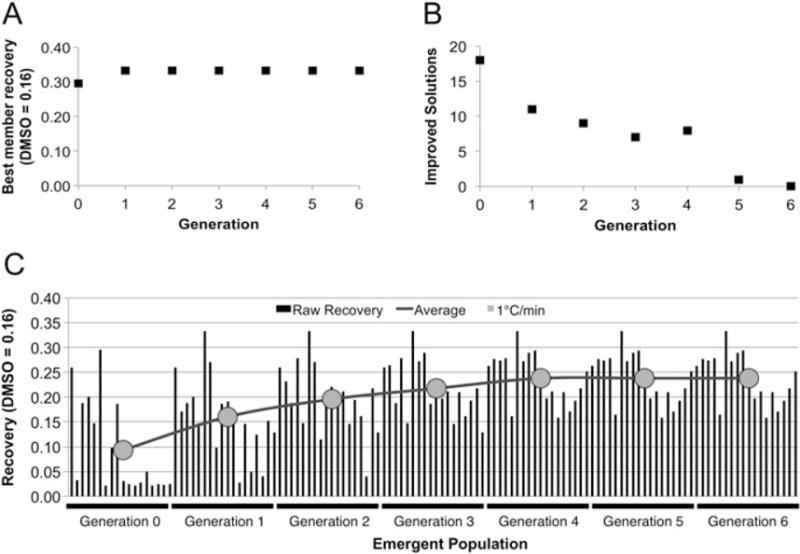
Trehalose, glycerol, ectoine 1°C/min DE algorithm results for Jurkat cells. (A) Cumulative best member solution; recovery associated with the best solution increases and plateaus as the algorithm converges. (B) Number of improved solutions/generation; the number of improved solutions in each generation decreases and reaches zero when the algorithm has converged. (C) Emergent population with the generational average overlaid: the emergent population improves and eventually stops changing as the DE algorithm converges; this is reflected in the generational average, which increases and begins to plateau as the algorithm converges. The optimum composition identified by this run of the algorithm was 150 mM trehalose, 10% glycerol, 0.1% ectoine for Jurkat cells frozen at 1°C/min

3.2. Optimizing both composition and cooling rate

Cooling rate influences cell survival (Leibo and Mazur, 1971) and optimal cooling rate varies with the composition of the freezing medium and the cell type being frozen (Mazur, 1984). Therefore, the optimal TGE solution composition identified for Jurkat cells at a constant cooling rate of 1°C/min may not be the optimum composition at other cooling rates, and thus may not produce the highest recovery possible. To optimize both composition and cooling rate in this study, the DE algorithm was programmed to output 27 vector solutions/generation with weight = 0.85 and crossover =1, using cooling rate as an additional optimization variable. Solutions were separated into categories based on their DE algorithm defined cooling rate, and were frozen in batches at these cooling rates (0, 0.5, 1, 3, 5 and 10°C/min). The results were normalized and scaled raw recovery is reported, allowing results from all cooling rates and all generations to be compared directly.

As with previous studies, the best member scaled raw recovery increased or remained constant with increasing iterations (Figure 3A) and the number of improved solutions within each generation tended to decrease (Figure 3B). The number of solutions frozen at given cooling rates is described by pie charts overlaid at the average recovery of each generation in Figure 3C. These pie charts show that the DE algorithm quickly identifies poor recovery in solutions frozen at 0° C/min (no freezing, recovery =0) and 0.5°C/min and eliminates these rates after 2 generations. In early generations, the majority of solutions with high recovery used cooling rates of 5 and 10°C/min. However, a spike in the number of 1°C/min solutions occurs in generation 4 after the DE algorithm identifies the same high recovery 1°C/min composition from the constant cooling rate study described in Figure 2 above. Ultimately, at convergence, this DE algorithm run identified that a TGE solution containing 300 mM trehalose, 10% glycerol, 0.01% ectoine at a cooling rate of 10° C/min resulted in optimum cell recovery for Jurkat cells (35% recovery in TGE at 10°C/min vs 16% = highest observed recovery in 10% DMSO at 1° C/min). The DE algorithm converged after seven generations (or eight freezing experiments).

Figure 3.

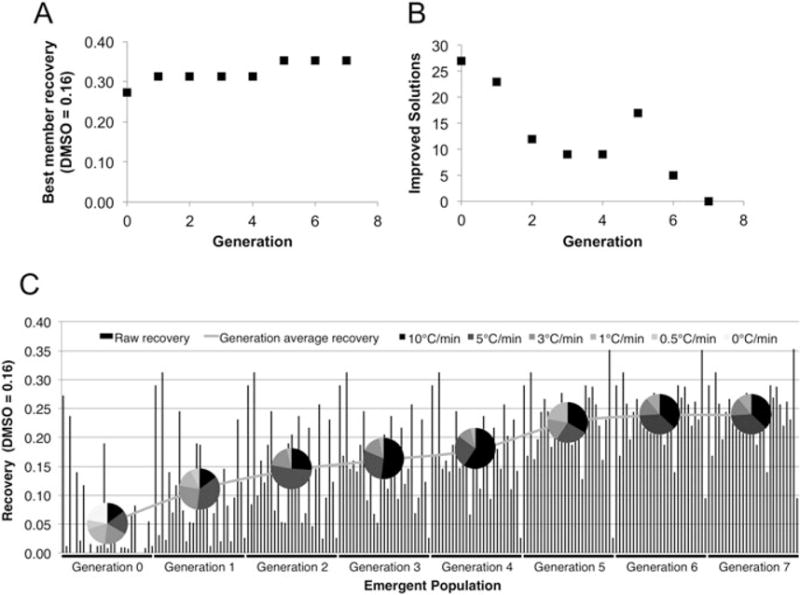
Trehalose, glycerol, ectoine cooling-rate DE algorithm results for Jurkat cells. (A) Cumulative best member solution; this increases and plateaus as the DE algorithm converges. (B) Number of improved solutions/generation; this decreases until it reaches zero as the DE algorithm converges. (C) Emergent population with the generational average overlaid: pie charts at each average show the cooling rate distribution within each generation. The optimum composition identified by this run of the DE algorithm was 300 mM trehalose, 10% glycerol, 0.01% ectoine at 10°C/min cooling

3.3. Confirmation of the optimum using high-throughput screening over the range of concentrations tested

High-throughput screening of solution compositions was used to confirm that the DE algorithm converged on the true optimum solution composition for a given cooling rate and component concentrations. Samples were frozen and thawed at 10°C/min. Serial dilutions of glycerol and ectoine were combined with dilutions of trehalose and cells suspended in Normasol-R™ in 96-well plates. The final concentrations in each well were equal to the full factorial array of concentrations used in the DE algorithm. The results from each well were normalized to a DMSO control included on each plate. This experiment was repeated in triplicate and the recovery results from each individual composition were averaged and are plotted in Figure 4 (SDs were typically <5%). This study confirmed that a composition of 300 mM trehalose, 10% glycerol, 0.01% ectoine resulted in the highest recovery for the array tested, indicating that the DE algorithm correctly identified the optimum of the system at 10°C/min.

Figure 4.

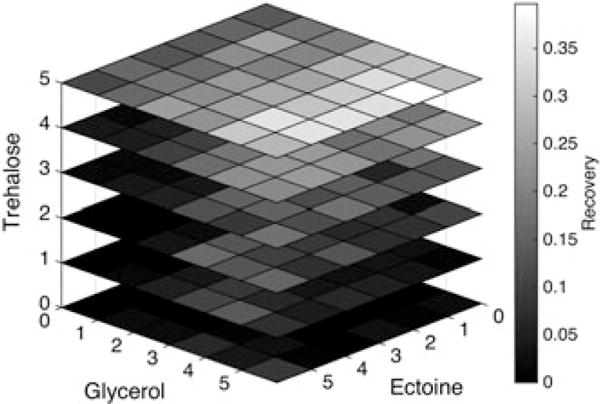
High-throughput concentration study confirmation of Jurkat DE algorithm results. Greyscale shades corresponding to recovery values are plotted in squares corresponding to solution compositions within the algorithm parameter space. This concentration study, performed at 10°C/min, identified the solution composition associated with maximum recovery to be 300 mM trehalose, 10% glycerol and 0.01% ectoine (corresponds to the points 5-trehalose, 5-glycerol, 1-ectoine in the heat map above). This composition is the same as the composition identified by the DE algorithm, confirming that it is indeed the optimum within the parameter space at 10°C/min

3.4. DE algorithm can be applied to different cell types, using different compositions and different numbers of solution components

The previous studies describe a three-component TGE solution tested with Jurkat cells. To show that the DE algorithm is capable of converging to freezing solution compositions using different solution components and different cell types, a five-component combination of sucrose, ethylene glycol, alanine, taurine and ectoine (SEGA) was tested with mesenchymal stem cells at DE algorithm-defined concentrations and cooling rates. These components were selected based on pre-screening experiments performed to identify combinations with high potential recovery. The DE algorithm was programmed to output 27 vector solutions/generation with weight = 0.85 and crossover =1. Experimental testing and result normalization were similar to the methods described above.

As with previous experiments, the cumulative best member composition increased and the number of improved solutions decreased with each generation. At convergence, this run of the DE algorithm identified that a SEGA solution of 300 mM ethylene glycol, 1 mM taurine and 1% ectoine resulted in optimum cell recovery for MSCs (40% recovery at 1°C/min vs 21% recovery in 10% DMSO at 1°C/min). Total convergence occurred after nine generations (10 freezing experiments), as evidenced by the increase and plateau of the best member recovery (Figure 5A) and the decrease in the number of improved solutions/generation (Figure 5B). It is noteworthy that two of the components tested (sucrose and alanine) were not present in the final solution formulation, indicating that the presence of these additives did not improve post-thaw survival at this cooling rate.

Figure 5.

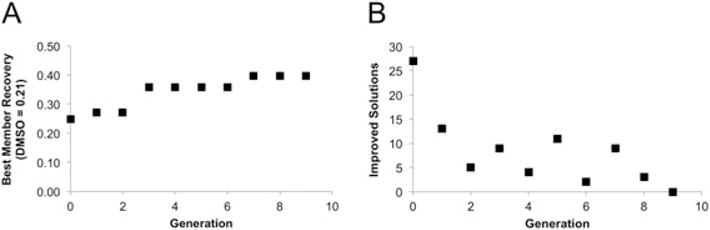
Sucrose, ethylene glycol, alanine, taurine, ectoine cooling-rate algorithm results for MSCs. (A) Cumulative best member solution; this increases and plateaus as the DE algorithm converges. (B) Number of improved solutions/generation; this decreases until it reaches zero as the DE algorithm converges. The optimum composition identified by this run of the DE algorithm included 300 mM ethylene glycol, 1 mM taurine, 1% ectoine with a 1°C/min cooling rate

3.5. Convergence results obtained for 96-well studies scale to larger volumes and are unique to the cell type being frozen

Freezing experiments were performed in 1 ml vials to determine whether the results with low volumes and small cell numbers in 96-well studies were reproducible when using larger, more clinically relevant volumes. DE algorithm solutions that resulted in maximum recovery were identified for both Jurkat cells and MSCs at 10°C/min. These solutions are identified as TGE 10°C (300 mM trehalose, 10% glycerol and 0.01% ectoine at 10°C/min optimized as above for Jurkat cells) and SEGA 10°C (150 mM sucrose, 300 mM ethylene glycol, 30 mM alanine, 0.5 mM taurine and 0.02% ectoine at 10°C/min optimized for MSCs). These solutions were combined with cells, frozen, thawed and analysed for viability as described in Materials and methods. A minimum of nine samples was analysed for each solution (batches of three or more on at least 3 different days). These were compared to solutions of cells in 10% DMSO frozen at 1°C/min (the gold standard for both cell types, labelled DMSO 1°C).

The TGE 10°C solution resulted in significantly higher viability than SEGA 10°C and the DMSO 1°C control (Figure 6A; DMSO 1°C = 0.90 ± 0.02; TGE 10°C = 0.95 ± 0.03; SEGA 10°C = 0.89 ± 0.03; p < 0.05) for Jurkat cells. Recovery was high across the board (> 88%) but not statistically significantly different for any of the solutions tested with Jurkat cells (Figure 6B; DMSO 1°C = 0.91 ± 0.04; TGE 10°C = 0.88 ± 0.15; SEGA 10°C = 0.88 ± 0.13; p < 0.05). Conversely, MSC viability testing showed no statistically significant differences between solutions (Figure 6C; DMSO 1°C = 0.96 ± 0.02; TGE 10°C = 0.92 ± 0.07; SEGA 10°C = 0.96 ± 0.02; p < 0.05), while the SEGA 10° C solution produced significantly higher recovery than either TGE 10°C or DMSO 1°C (Figure 6D; DMSO 1° C = 0.90 ± 0.12; TGE 10°C = 0.88 ± 0.11; SEGA 10° C = 1.03 ± 0.15; p < 0.05). This indicates that optimization results for individual cell types are unique and can result in significantly higher viability (Figure 6A) or recovery (Figure 6D). However, both TGE and SEGA solutions produced acceptable viability and recovery in cell types for which they were not optimized, indicating that DE algorithm-optimized solutions may be used to freeze multiple cell types successfully. Follow-up studies currently being performed suggest that cells frozen with these solutions proliferate post-thaw at rates similar to cells frozen in DMSO.

Figure 6.

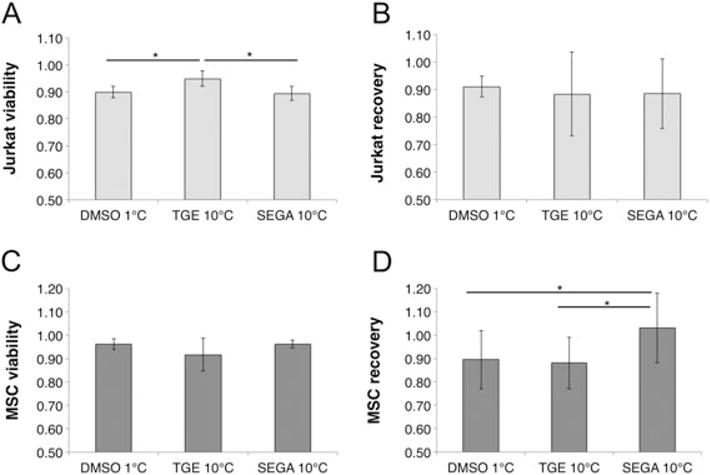
Scale-up viability and recovery of Jurkat cells (A, B) and mesenchymal stem cells (C, D) frozen in DE algorithm-optimized solutions. Each cell type was frozen at 10°C/min in a TGE solution optimized for Jurkat cells (TGE 10°C) and a SEGA solution optimized for MSCs (MSC 10°C). Results were compared to cells frozen in DMSO at 1°C/min (DMSO 1°C), as it represents the current gold standard for both cell types. Jurkat cells performed well in both the SEGA 10°C and TGE 10°C solutions, and Jurkat cell viability was significantly higher in TGE 10°C than both SEGA 10°C and the DMSO 1°C control (A). MSCs also performed well in both SEGA 10°C and TGE 10°C solutions, and had significantly higher recovery in the SEGA 10°C solution than both TGE 10°C and the DMSO 1°C control (D). Significance markers indicate p < 0.05

Figure 6 also shows that DE algorithm optimization results are scalable. Although the improvement in recovery for optimized solutions in comparison to DMSO is smaller in vial studies than in 96-well studies, this result is expected because of the limited difference that is possible when recovery and viability are high. Cumulatively, these results support DE algorithm testing of small volumes of cells and solutions, as optimized solutions produce high viability and recovery at larger volumes.

4. Discussion

Current methods of optimizing cryopreservation solutions most often use empirical methods, by testing a given composition and cooling rate and measuring post-thaw recovery (Conrad et al., 2000; Dijkstra-Tiekstra et al., 2014; Dong et al., 2009; Freimark et al., 2011; Kearney et al., 1990). Our studies show that optimization of freezing solutions can be performed using a DE algorithm. The DE algorithm can be used for different cell types and can concurrently optimize both solution composition and cooling rate. The three variables examined in this study (cryoprotectants, cryoprotectant concentration and cooling rate) represent only a subset of the variables that can be considered when optimizing a cryopreservation protocol. In the future, rate of addition and removal of cryoprotectants, temperature of nucleation, incubation time, hold temperature, single vs multistep cooling, storage temperature and thawing rate are all parameters that could be incorporated into this type of algorithm optimization.

The use of DE to optimize over a multiparametric space has been used in a wide variety of fields. Recently, Tsutsui et al. (2011) used this approach to optimize a defined medium for the culture of human embryonic stem cells.

The investigation described above utilizes DE as part of an innovative method to optimize both cooling rate and composition for the cryopreservation of therapeutic cell types. This DE algorithm used a total of seven to nine experiments to optimize a three- or five-component solution. The DE algorithm as implemented rapidly optimized both solution composition and cooling rate with <200 unique experimental points; without the aid of the DE algorithm, ~7000 unique experimental data points would have been required to optimize the compositions tested above. Best member solutions increased and the number of improved solution compositions steadily decreased with advancing generation, consistent with convergence of the DE algorithm. Convergence to a local optimum was confirmed by high-throughput studies using the same components and the same range of concentrations as the DE algorithm. The data here suggest that the DE algorithm can reliably optimize at least six parameters at a time (Figure 5 shows that the DE algorithm optimized five solute concentrations and a cooling rate) and more parameters could theoretically be added if the population size within each generation is increased and the number of generations tested is increased to ensure that convergence is reached.

The ability to cryopreserve cells in a 96-well format enabled the testing of generations with a large number of solutions (18–27). Freezing of cells in 96-well format has been used to improve the post-thaw recovery of anchorage-dependent cells (Katkov et al., 2011). Cells cryopreserved in a 96-well format are also available commercially and used for drug screening and other applications. In this study, post-thaw recovery of cells frozen in DMSO was lower for cells frozen in 96-well plates vs vials. The same was true for cells frozen in DMSO-free solutions. One possible explanation for this reduced viability is the slower warming rates observed for plates vs vials; 96-well plates had an average sample warming rate of 1.30°C/s (−196°C to 0°C in 150 s), while vials had an average sample warming rate of 1.63°C/s (−196°C to 0°C in 120 s). A second possible explanation for the reduction in recovery observed in 96-well plates could be due to the extended post-thaw incubation time for cells in 96-well plates. Cells in 96-well plates were subject to an additional 30 min of incubation post-thaw in 0.5× cryopreservation solutions after viability dye was added (allowing it time to be metabolized by live cells), while 1 ml vials were assessed for recovery immediately using AO/PI. However, the recovery trends observed in 96-well plates were scalable to larger volumes, in that the differences in viability and recovery between experimental solutions and DMSO were comparable. Cumulatively, these results support DE algorithm testing of small volumes of cells and solutions, as optimized solutions produced high viability and recovery at larger, more clinically relevant volumes. Additional metrics of cryopreservation success, such as proliferation, alignment, gene expression, etc., could easily be incorporated as the input of the algorithm, rather than using recovery.

Preservation of Jurkat cells and MSCs is principally performed using 10% DMSO and a cooling rate of 1° C/min. A limited number of studies have examined vitrification of MSCs (Moon et al., 2008; Todorov et al., 2010) and the use of polymers to replace DMSO (Matsumura et al., 2010). This investigation describes novel formulations in which solutions with multiple components are known to preserve cell viability. Glycerol is used for the cryopreservation of red blood cells (Valeri et al., 2000) and was the first cryoprotective agent discovered (Polge et al., 1949). Similarly, trehalose has been shown to be an effective cryoprotective agent (Crowe and Crowe, 2000). What makes this investigation noteworthy is that the combination of two or more cryoprotectants is effective and that effectiveness is not necessarily observed at the highest concentrations tested. Additionally, these multi-component compositions result in cell viability and recovery significantly higher than 10% DMSO, which is an important step forward towards DMSO-free cryopreservation.

Additional studies will be needed to characterize the methods of action for these multicomponent solutions. These studies are enabled by the development and implementation of the DE algorithm, which permits optimization of a multicomponent solution in a rational, accelerated fashion.