Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2018 Jan 16;9:233. doi: 10.1038/s41467-017-02597-8

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© The Author(s) 2018

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

PMC Copyright notice

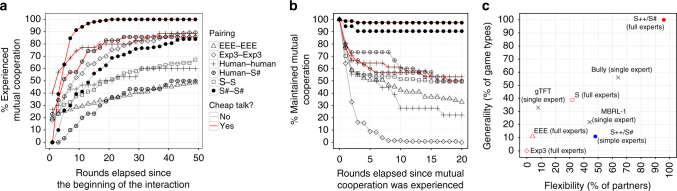
Fig. 7 — Comparisons of people and algorithms with respect to various characteristics. a Empirically generated cumulative-distribution functions describing the number of rounds required for pairings to experience two consecutive rounds of mutual cooperation across three games (Chicken, Alternator Game, and Prisoner’s Dilemma). Per-game results are provided in Supplementary Note 7. For machine–machine pairings, the results are obtained from 50 trials conducted in each game, whereas pairings with humans use results from a total of 36 different pairings each. b The percentage of partnerships for each pairing that did not deviate from mutual cooperation once the players experienced two consecutive rounds of mutual cooperation across the same three repeated games. c A comparison of algorithms with respect to the ability to form profitable relationships across different games (Generality) and with different associates (Flexibility). Generality was computed as the percentage of game types (defined by payoff family × game length) for which an algorithm obtained the highest or second highest average payoffs compared to all 25 algorithms tested. Flexibility was computed as the percentage of associates against which an algorithm had the highest or second highest average payoff compared to all algorithms tested. See Supplementary Note 3 for details about each metric