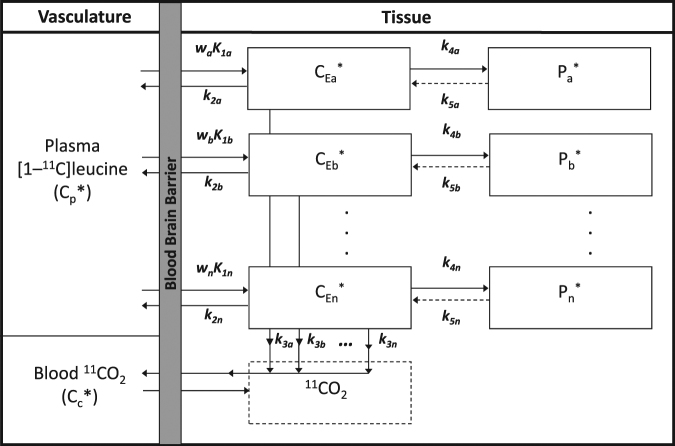
Figure 2.

Heterogeneous Tissue Model for L-[1-¹¹C]Leucine PET method. The heterogeneous tissue model²⁰ for the labeled leucine assumed that each tissue is composed of n kinetically homogenous subregions (a,b,…,n), each described by the homogeneous tissue model of Fig. 1. The corresponding fractional weights of the subregions are w_a w_b, … w_n (w_a ≥ 0, w_b ≥ 0, …, w_n ≥ 0; n ≥ 1; w_a + w_b + … + w_n = 1). Total activity in the heterogeneous region as a whole can therefore be described by the weighted sum of the activities in each of the subregions. Expressed in terms of rate constants we have: $\begin{array}{l}{C}_T^{⁎}\left(t\right)={\theta }_0{\int }_0^t{C}_p^{⁎}\left(\tau \right)d\tau +{\theta }_a{\int }_0^t{C}_p^{⁎}(\tau )e^{-{\beta }_a\left(t-\tau \right)}d\tau +\dots +{\theta }_n{\int }_0^t{C}_p^{⁎}\left(\tau \right)e^{-{\beta }_n\left(t-\tau \right)}d\tau \\ +V_b\left[C_b^{⁎}\left(t\right)-V_D{C}_c^{⁎}\left(t\right)\right]+V_D{C}_c^{⁎}(t)\end{array}$ where ${\theta }_0=(1-V_b){\sum }_{i=a}^n\left[\frac{w_i{K}_{1i}{k}_{4i}}{k_{2i}+k_{3i}+k_{4i}}\right],$ ${\beta }_i=k_{2i}+k_{3i}+k_{4i},$and ${\theta }_i=(1-V_b)\left[\frac{w_i{K}_{1i}(k_{2i}+k_{3i})}{k_{2i}+k_{3i}+k_{4i}}\right]fori=a,b,\dots ,n.$ If n, θ₀, θ_i (i = a, b, …, n) and V_b are known, or have been estimated, then the above equations can be used to determine the weighted average influx rate constant for the mixed tissue, K₁ = w_aK_1a + w_bK_1 b+ … +w_nK_1n, as $K_1=\frac{{\theta }_0+{\sum }_{i=a}^n{\theta }_i}{\left(1-V_b\right)}$. Note that we cannot identify the individual subregion’s weighted influx rate constant w_iK_1i, but only the sum over all subregions. Nor can the fraction of unlabeled leucine derived from arterial plasma in each individual subregion, i.e., λ_i = (k_2i + k_3i)/(k_2i + k_3i + k_4i), be identified as this fraction appears in the equation for θ_i only as the product with the non-identifiable term w_iK_1i. However, regional variations in measured values of λ are small¹⁸ and the parameter can be assumed constant across subregions, (i.e. λ = λ_a = λ_b = … = λ_n), resulting in$\lambda =\frac{{\sum }_{i=a}^n{\theta }_i}{{\theta }_0+{\sum }_{i=a}^n{\theta }_i}$ Weighted average rCPS is then given by $\mathrm{rCPS}=\left(\frac{w_a{K}_{1a}{k}_{4a}}{k_{2a}+k_{3a}}+\frac{w_b{K}_{1b}{k}_{4b}}{k_{2b}+k_{3b}}+\dots +\frac{w_n{K}_{1n}{k}_{4n}}{k_{2n}+k_{3n}}\right)C_p=K_1\left[\frac{1-\lambda }{\lambda }\right]C_p.$