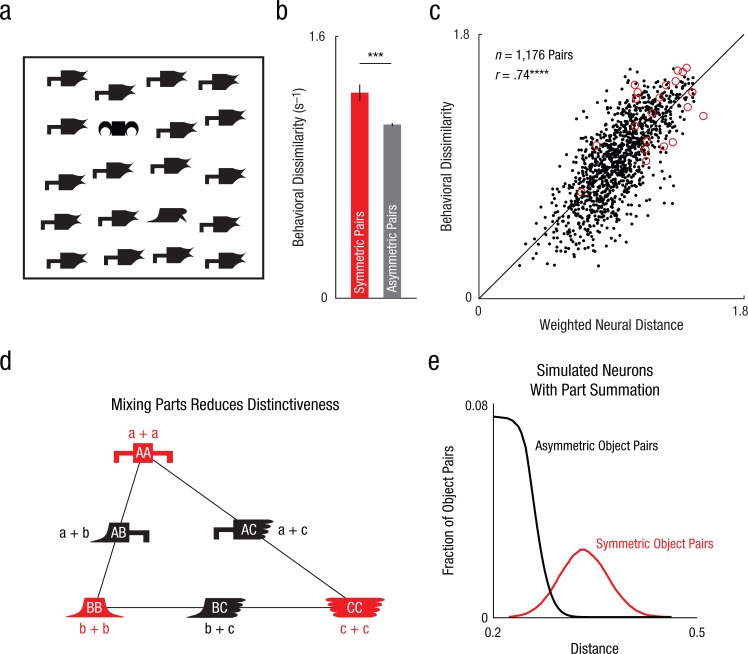
Fig. 3.

Distinctiveness of symmetric objects as a result of part summation. The example search array from Experiment 1 (a) contains a symmetric oddball and an asymmetric oddball embedded among asymmetric distractors. The symmetric object is easier to find than the asymmetric object, even though both objects differ in two parts from the distractors. The bar graph (b) shows mean behavioral dissimilarity for symmetric object pairs and equivalent asymmetric object pairs measured using visual search in humans (Experiment 1). The asterisks indicate a significant difference between pair types (***p < .0005). Error bars represent ±1 SEM calculated on object pairs (n = 21 for symmetric objects; n = 420 for asymmetric objects). The scatterplot (c; with best-fitting regression line) shows behavioral dissimilarity for each pair of objects (in humans; Experiment 1) plotted against weighted neural dissimilarity across inferior temporal (IT) neurons (in monkeys), separately for symmetric object pairs (circles) and asymmetric object pairs (dots). The asterisks indicate a significant correlation (****p < .00005). The schematic (d) illustrates how part summation results in greater distinctiveness. Let parts A, B, and C evoke neural activity represented by vectors a, b, and c. According to part summation, the response to any object AB will be a + b. As a result, the symmetric objects AA, BB, and CC will evoke activity 2a, 2b, and 2c, whereas the asymmetric objects AB, BC, and AC will evoke activity a + b, b + c, and a + c. The response to each asymmetric object pair (e.g., AB) will lie at the midpoint of the line joining the two symmetric object pairs (e.g., AA and BB). As a result, the asymmetric objects AB, BC, and AC will evoke more similar activity than symmetric objects AA, BB, and CC. In other words, combining different parts in an object reduces its distinctiveness, just like mixing paints, whereas combining similar parts in an object maintains the original distinctions between the parts. This simple property causes symmetric objects to be farther apart in general than asymmetric objects, while producing no net difference in the average response to symmetric and asymmetric objects. To confirm that this extends to many neurons with heterogeneous selectivity, we created 50 artificial neurons with identical part responses at both locations, but with random part selectivity, and used them to generate whole-object responses. The plot (e) shows the distribution of distances for symmetric object pairs and asymmetric object pairs.