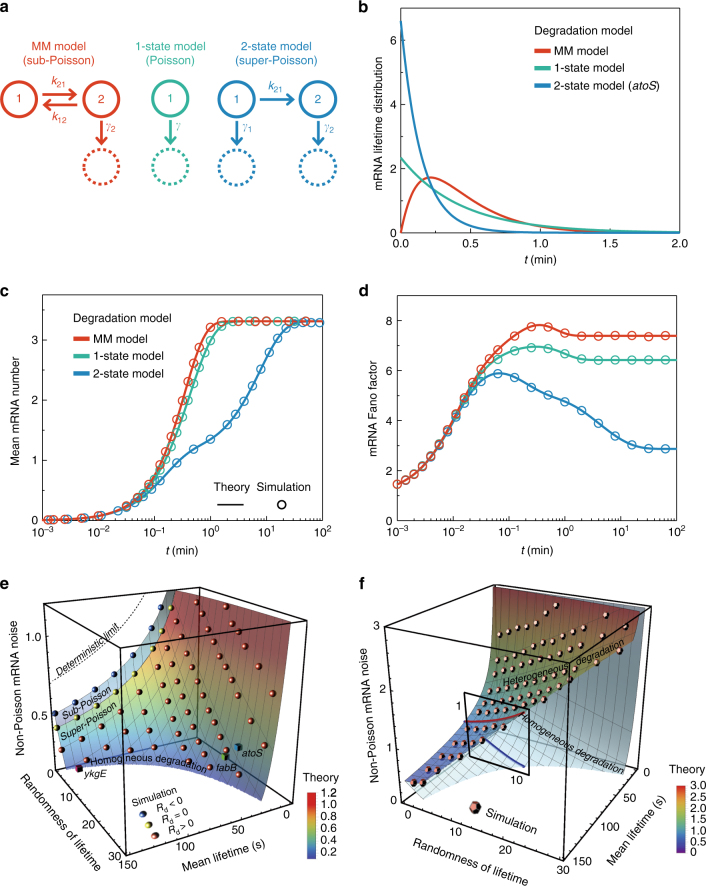
Fig. 5.

Quantitative prediction for mRNA noise dependence on mRNA lifetime fluctuation. a Models of the mRNA degradation process: (left) the Michaelis–Menten sub-Poisson process; (middle) one-state Poisson process; (right) two-state super-Poisson process. mRNA degradation starts from state 1. The three models represent renewal processes with different distributions of mRNA degradation time. Randomness, R_d, in mRNA degradation time or lifetime is defined by the relative variance of mRNA lifetime minus unity. For sub-Poisson mRNA degradation, R_d < 0; for a Poisson process, R_d = 0; and for a super-Poisson process, R_d > 0. b mRNA lifetime distributions. (red line) Michaelis–Menten (MM) sub-Poisson process; (green) 1-state Poisson process; (blue line) 2-state super-Poisson process (Supplementary Note 16). The 2-state super-Poisson model has been used to model the bi-exponential lifetime distribution of atoS, fabB, and ykgE mRNA^63–65. The mean mRNA lifetime is set equal to 25.8 s, the mean lifetime of atoS mRNA. c, d Time dependence of the mean and Fano factor in the number of mRNA transcribed by a single gene. The mean and Fano factor of mRNA number are calculated from equation (M1-6) and Eq. (1) for Model III, optimized from our analysis in Fig. 2 for experimental data obtained from slowly growing E. coli³⁶ (see Supplementary Table 1). The fraction of the active gene state is set to 1/2. e, f Dependence of the steady-state non-Poisson mRNA noise on the mean and randomness of the mRNA lifetime for two models: for the two-state super-Poisson mRNA degradation model without cell-to-cell heterogeneity (e) and for the 1-state Poisson mRNA degradation model, but with cell-to-cell heterogeneity in the rate (f). The theoretical prediction is made by the CFT in e, but by the generalized CFT, equation (M8-5) in f. (surface) Theoretical prediction. (spheres) Simulation results. (cubes) Prediction for atoS, fabB, and ykgE mRNA transcribed under IPTG inducible lac promoter in slowly growing E. coli shown in Fig. 2, given the 2-state super-Poisson model of mRNA degradation is valid⁶⁶. Non-Poisson mRNA noise is measured by $\Delta \left(x\right)\left[\equiv Q_n∕{⟨n⟩}_1-Q_n∕{⟨n⟩}_1{\mid }_{x=1}\right]$, or the mean mRNA number dependent component of non-Poisson mRNA noise produced by single-gene transcription (see Supplementary Note 6). Both models yield the same bi-exponential mRNA lifetime distribution. mRNA noise increases with the randomness in the mRNA lifetime originating from cell-to-cell heterogeneity in the mRNA degradation rate, but decreases with an increase in the randomness of mRNA lifetime caused by non-Poisson mRNA degradation dynamics (Supplementary Note 4 and Supplementary Movies 1 and 2)