Analyzing Distributional Learning of Phonemic Categories in Unsupervised Deep Neural Networks

Abstract

Infants’ speech perception adapts to the phonemic categories of their native language, a process assumed to be driven by the distributional properties of speech. This study investigates whether deep neural networks (DNNs), the current state-of-the-art in distributional feature learning, are capable of learning phoneme-like representations of speech in an unsupervised manner. We trained DNNs with unlabeled and labeled speech and analyzed the activations of each layer with respect to the phones in the input segments. The analyses reveal that the emergence of phonemic invariance in DNNs is dependent on the availability of phonemic labeling of the input during the training. No increased phonemic selectivity of the hidden layers was observed in the purely unsupervised networks despite successful learning of low-dimensional representations for speech. This suggests that additional learning constraints or more sophisticated models are needed to account for the emergence of phone-like categories in distributional learning operating on natural speech.

Introduction

Acquisition of the native language phonemic system is an important step in early language acquisition, enabling a transition from generic auditory perception towards symbolic and generative representation of words and subword units. Although it is known that infants adapt to the distributional characteristics of their native language sound system during their first year of life (Werker & Tees, 1984), it is less obvious whether early perceptual representations of speech actually consist of sequential invariant atomic units such as phones or phonemes before lexical learning, or whether adult-like phonemic system emerges only through extensive experience and learning at multiple levels of language representations (c.f., Werker & Curtin, 2005; see also Räsänen & Rasilo, 2015, for a recent overview).

Since distributional learning can be framed as unsupervised machine learning from speech data, a number of computational studies have investigated how phone categories could be clustered from acoustic speech input only and how selective these automatically discovered sound categories are (e.g., de Boer & Kuhl, 2003; Vallabha, McLelland, Pons, Werker, & Amano, 2007; Kouki, Kikuchi & Mazuka, 2010). These studies have typically limited their analysis to pre-segmented or otherwise carefully selected subsets of speech tokens and/or phone categories. In addition, they have enforced an explicit clustering procedure of potentially infinitely many different acoustic tokens into a finite number of discrete and disjoint phone classes. The general finding has been that these acoustic clusters tend to be selective towards specific phones but are far from a representational system that would be invariant to non-phonological acoustic variability across talkers, speaking styles, and other factors. Due to the challenges in bottom-up clustering speech directly into phonemic categories, a number of computational models (e.g., Feldman et al. 2013; Elsner et al., 2012) and theoretical frameworks (e.g., Werker & Curtin, 2005; Räsänen & Rasilo, 2015) propose that phonemic learning is inherently tied to concurrently emerging lexical knowledge and should not be considered as an isolated process strictly preceding word learning.

Despite the emerging view that phonemic learning cannot be addressed in isolation from lexical learning, it is still important to understand how different aspects of language experience affect the development of speech perception capabilities. One of these aspects is the question of how much of early adaptation to one’s native language can still be driven by purely auditory statistics. In the present study, we investigated whether deep neural networks (DNNs), a set of powerful machine learning techniques for feature learning, are capable of extracting phoneme-like representations from continuous speech similarly to their capability of learning mammalian-like visual receptive fields from image data. More specifically, we asked whether the representations resulting from unsupervised distributional learning of speech reflect phonemic contrasts of the language when the network is forced to discover low-dimensional re-presentations of the initially high-dimensional acoustic space, i.e., whether phonemic variation dominates other distributional properties of natural continuous speech.

Deep neural networks and phonemic learning

Deep neural networks, which are artificial neural networks with two or more hidden layers, are the current state-of-the-art in the discovery of non-linear structure (or features) from stochastic data (Hinton, 2014). They have also been shown to provide good approximations for the emergence of increasingly abstract visual features in mammalian visual pathway (e.g., Cichy et al., 2016). In the context of speech, DNNs have become the state-of-the-art acoustic models in standard automatic speech recognition (ASR) systems due to their scalability and representational power in comparison to the previously used shallow models such as Gaussian-mixture models. In addition, purely unsupervised deep autoencoder networks (see Methods) have been shown to be effective for learning low-dimensional representations from high-dimensional acoustic input in the absence of any supporting linguistic information (e.g., Deng et al., 2010).

In the previous work, Nagamine, Seltzer, and Mesgarani (2015) showed that hidden layers of a feedforward neural network become increasingly selective to phone categories and phonetic features when trained on continuous speech. The selectivity observed in the DNN was also found to be similar to the phonemic selectivity observed in the human superior temporal gyrus (Mesgarani et al., 2014). However, Nagamine et al. trained their network in a supervised manner using phonetic labels of the input acoustic vectors as targets for the DNN output layer. This means that the entire network was optimized to perform discrimination of the acoustic input in terms of the given phonetic categories–the standard approach taken in ASR.

In contrast to supervised learning, concurrent phonetic labeling of speech input is not available to infants learning their native language. The previous study therefore leaves open whether similar increasingly abstract phonemic structure can also emerge from purely auditory learning when the neural network attempts to find a low-dimensional but high-fidelity code for the incoming acoustic input. If so, this would provide evidence for how much of the native phonemic invariance properties can be acquired simply by listening to speech in the absence of any further constraints and give insight to the type of “receptive fields” that become responsible for phonemic perception. On the other hand, a failure to learn increasingly invariant phonemic representations from acoustic input would suggest that local short-term dependencies of speech, as captured by the feedforward networks, would be insufficient for the emergence of phonemic categories and that additional constraints from concurrently emerging knowledge at different levels (e.g., Feldman et al., 2013; Räsänen & Rasilo, 2015) or different network topologies are needed in the learning process (see, e.g., Synnaeve et al., 2014).

In order to investigate whether DNNs as hierarchical generative models of speech are capable of acquiring some type of invariance properties with respect to phonetic or phonemic representations of the input speech, we conducted a number of learning simulations using the existing standard unsupervised DNN architectures.

Methods

Speech input to the DNNs was represented using logarithmic Mel-spectral features similarly to the earlier work (Nagamine et al., 2015). The input signal was converted to 10-ms feature frames x_t using a sliding 25-ms window and computing 24-band log-Mel-spectrum from each window. The features were Z-score normalized across each utterance to ensure proper scaling for neural network input. The final inputs to the networks were formed by concatenating 11 subsequent Mel-spectrum frames x_t to a single input vector f_t = [x_t−5, x_t−4, …, x_t+5]^T. Unlike Nagamine et al. (2015), we decided to leave out the first and second derivatives of the Mel-spectra since the resulting time-frequency patches already contain local temporal dynamics of the input (as confirmed by the replication of the earlier findings; see the Experiments section).

Three standard DNN architectures were investigated in the present work: 1) a supervised deep multilayer perceptron (MLP) for classification of speech to phone labels (replication of the previous work by Nagamine et al., 2015), 2) a stack of unsupervised restricted Boltzmann-machines (RBMs) that learn a generative model over the input data, the entire stack referred to as a deep belief network (DBN), and 3) an unsupervised deep feed-forward autoencoder network (AEN) that learns to map input speech into a low-dimensional bottleneck-layer and then expand (decode) that representation back to a reconstruction of the original input.

The use of DBNs and AENs to study distributional phonetic learning was motivated by the finding that DBNs are capable of learning increasingly abstract visual features from image data (Hinton & Salakhutdinov, 2006) and achieve superior dimensionality reduction performance in comparison to linear models such as PCA in many tasks. The assumption in the present study is that the phonemic identity of the speech segments might require fewer bits to encode than the details of the acoustic input itself, and therefore a generative network with a decreasing number of nodes in the higher and narrower layers should become more “phonemic” in its representation when dimensionality reduction is imposed on the data. This is, of course, only if the variance in the acoustic input is best explained across dimensions correlated with phonemic identities instead of some other low-dimensional description of the input, and that the learning algorithms used to estimate DNN parameters are capable of finding this manifold.

In our experiments, the MLP was trained in the standard way using acoustic feature vectors f_t as input to the network with H hidden layers, computing the activation of the output layer h_out,t given the input, and then calculating the error of the activation with respect to a target vector g_t denoting the phonemic identity of the input vector. The weights of the network were then tuned using backpropagation (BP) algorithm in order to minimize the error of the output layer (Rumelhart, Hinton & Williams, 1986).

DBNs were obtained by first training a three-layered stack of RBMs incrementally layer-by-layer, always fully training the parameters of an RBM with one hidden layer at a time (Fig. 1), then freezing those parameters and using the probabilities of the hidden unit activations given the training data as the “visible layer” input to the next hidden layer. As a result, the stack becomes a hierarchical generative model P(f | h) over the training data with higher hidden layer activations h representing increasingly complex features of the input data (see Hinton & Salakhutdinov, 2006).

Figure 1.

A schematic description of how pre-trained RBMs are “unrolled” to five-layer feedforward DBN and AEN networks used in the present study. Weights after layer-by-layer RBM pre-training are shown with black W and weights after error backpropagation (BP) are shown with blue W. The baseline supervised MLP topology is shown on the right (adapted from Hinton & Salakhutdinov, 2006).

In order to obtain five-layered DBNs (as defined in the present study), the stack of RBMs was “unrolled” (Fig. 1) to a feed-forward network by mirroring the structure of the network on top of the low-dimensional bottleneck-layer with the output layer corresponding to a reconstruction of the input speech (see Hinton & Salakhutdinov, 2006). In this case, the three first layers correspond to the standard feed-forward activations of the original stacked RBM while the last two layers are identical to the top-down reconstructions of the same model.

Finally, AENs were obtained by fine-tuning the DBN weights using BP in order to minimize the Mel-spectrogram reconstruction error at the output of the network, therefore breaking the weight symmetry of the DBN.

All networks used sigmoid activation functions except for the output layer, which was always linear. In the case of MLP, instead of using the typical softmax output layer with multinomial labels, we experimented with distributed target representation by first assigning each of the unique phones c with a random vector sampled uniformly from v_c ~[0,1] ∈ R^d (d = 40). Then the distribution of phones within the input time window (W = 11 frames) was encoded to a target vector g_t as a weighted mean of the random vectors corresponding to the phone labels of the frames within the window:

$${\mathbf{g}}_t=\frac{1}{K}{\sum }_{i=t-(W-1)/2}^{t+(W-1)/2}{\mathbf{v}}_{t+i}$$ (1)

Since this type of random mapping preserves the approximate mutual distances between representations (Johnson & Lindenstrauss theorem) while the sum of high dimensional random vectors preserves information regarding the individual components (e.g., Kanerva, 2009), the approach enables creation of fully dense target vectors that represent arbitrary distributions of phones, and, in general, provides opportunities to incorporate structured target representations using fixed-dimensional outputs (see Gallant & Okaywe, 2013). DBNs always utilized a Gaussian input layer to accommodate the z-score-normalized input.

For the baseline MLPs, we used the same network configuration as in Nagamine et al. (2015) by using five hidden layers, each consisting of 256 nodes (Fig. 1, right). As for the DBNs and AENs, we initially experimented with a number of different network layouts and layer sizes using a subset of the training data, including bottleneck-architectures with gradually decreasing number of nodes in deeper layers, bottlenecks with different numbers of nodes, and even expanding networks with an increasingly many nodes at higher layers (see Table 1 for a summary). Since there were no major qualitative differences in the findings, one basic bottleneck layout of d = [256, 128, 32, 128, 256] nodes per layer for the DBN and AEN was chosen for more detailed analysis.

Table 1.

KNN performance (% correct) for phone and gender classification in TIMIT data for different hidden layers (L) in other tested unsupervised network topologies.

topology	L1	L2	L3	L4	L5
DBN [256 256 256 256 256]	62.0	59.0	56.7	55.2	54.6	phones
AEN [256 256 256 256 256]	64.0	59.9	64.2	65.0	64.6
DBN [256 512 1024 512 256]	61.4	60.2	58.2	57.0	56.0
AEN [256 512 1024 512 256]	62.4	61.5	64.9	65.7	65.5
DBN [128 64 8 64 128]	59.4	56.8	38.5	38.5	38.2
AEN [128 64 8 64 128]	60.6	57.4	55.6	55.5	55.5
AEN [256 256 256 256 256]	84.7	82.2	84.7	84.9	84.9	gender
AEN [256 512 1024 512 256]	84.6	83.7	85.5	86.5	86.0
AEN [128 64 8 64 128]	79.0	75.5	71.4	71.2	70.7

The dimension of the input layer for all networks and of the output layer for the AENs and DBNs was always 264 (11 frames x 24 frequency bands). In order to ensure that the training of the networks was successful, we always manually verified that the reconstruction or classification error decreased monotonically as a function of the epoch number during BP, and that the generative networks were capable of performing sensible reconstructions from the input Mel-spectrograms.

Data

Two qualitatively different corpora were used in the experiments in order to get a comprehensive picture of the learning process. The TIMIT corpus of American English read speech (Garofolo et al., 1993) was used as the primary dataset since the earlier work was evaluated on the same data and since TIMIT represents natural variation of speech across multiple talkers and dialects. The full training set of 4620 sentences was used to train the DNNs and the test set of 1620 sentences was used in the phonemic invariance analyses. Both sections contain speech from male and female talkers and the data is hand-labeled for phone segments.

In addition, we used enacted child-directed speech from the Caregiver (CG) Y2 UK corpus (Altosaar et al., 2010) to investigate whether results differ for limited-variability speech from a small vocabulary of approx. 80 words, each word repeated multiple times in the training set, and when all speech comes from a single talker (“a caregiver”). For this purpose, 1600 utterances from Talker-01 of the corpus were used to train the DNNs and a remaining set of 797 utterances were used to probe the phonemic selectivity of different layers. The CG UK Y2 corpus comes with a phone annotation created by forced-alignment from text to speech using an automatic speech recognizer. Due to the simplicity of the material, this reference can also be considered as highly reliable at the level of individual phones.

The data were randomly divided into a set of minibatches for training, each minibatch consisting of 100 samples for each RBM parameter update and 1000 samples for each BP update. In all simulations, BP was always run for 25 epochs similarly to Nagamine et al. (2015) whereas DBN-pretraining consisted of 15 epochs per layer.

Methods for network selectivity analysis

Activations of the networks were analyzed in the context of the underlying phone annotation. Original 61 phone classes of TIMIT annotation were first mapped to the reduced set of 39 phones and with silences and closures excluded (Lee & Hon, 1989). The set of 38 unique phones in the original CG annotation was used in its original form. In order to study phone-specific activations of the networks, only the test data input frames consisting of at least 90.9% of a single phone segment were included in the analysis, corresponding to 19706 samples on TIMIT test set and 4749 samples on the CG Talker-01 data.

Similarly to Nagamine et al. (2015), the activation of each layer in the context of different phone classes was analyzed using the F-ratio. First, the activation vectors consisting of all nodes within a layer of interest were grouped according to the phone labels associated with the inputs. The cross-phone variance of the node activations was then compared to the intra-phone variance, revealing whether the node activations for different realizations of the same phone are more similar than activations for two any arbitrary phone segments. By measuring the average F-ratio across layers, we can probe whether the activations for different allophones of the same phone class are more consistent in some layers than others. In addition to the F-ratio, we measured the mean mutual information (MI) between node activations and corresponding phone labels to see how many bits of information does each individual node, on average, contain regarding the phone classes of the input vectors.

Finally, k-Nearest Neighbor (KNN) classification of the layer-specific activations into phone categories was performed in order to evaluate how well the full pattern of activation in a layer discriminates between phone classes. More specifically, every activation h_i,t of layer i for input f_t was used as a single feature vector for classification (e.g., dim(h_i) = 256 in all hidden layers i of the MLP). Four-fold cross-validation performance with 75% of the vectors as training data and 25% of vectors as testing data was then computed. The parameter k was always varied between [1, 10] and the best result across this range was chosen as the classification accuracy for each fold before averaging the results across all folds. In addition to analyzing phone selectivity, we also included analyses of selectivity towards manner of articulation (MOA) and talker gender using the TIMIT data and the same set of measures.

Results

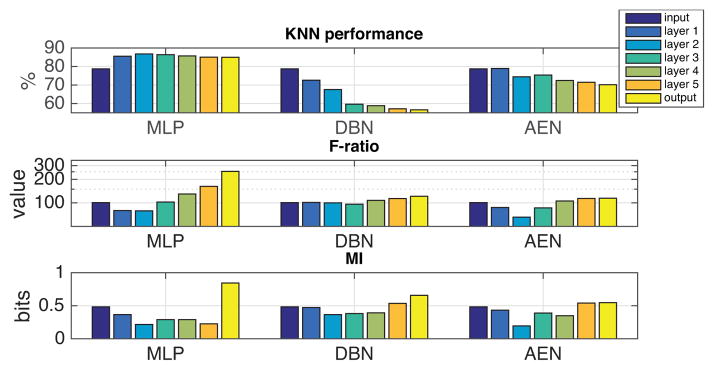
Fig. 2 shows the overall analysis results from the three different networks (supervised MLP, unsupervised DBN and AEN) for the TIMIT data with multiple talkers. Fig. 3 shows the corresponding results for the single-talker IDS speech from the CG corpus. Table 1 shows a summary of KNN-based phonetic discriminability of layer activations for alternative network topologies tested on TIMIT.

Figure 2.

Network invariance with respect to phones, manner of articulation (MOA), and speaker gender for multi-talker training. The supervised MLP network is shown on left, followed by the unsupervised pre-trained DBN (center), and the fine-tuned autoencoder (right). Top: KNN classification performance using layer activations as features. Middle: F-ratio of node activations w.r.t. sample classes of interest. Bottom: mutual information (MI) between classes and node activations. DBN and AEN shown for d = [256, 128, 64, 128, 256].

Figure 3.

DNN phone invariance measures for the CG single-talker data for different network types and layers. DBN and AEN shown for d = [256, 128, 64, 128, 256].

The first finding is that the supervised MLP replicates the earlier results of Nagamine et al. (2015) with increasing network layers showing higher selectivity towards phone classes (max. improvement of 11%) and less sensitivity to talker identity (gender), as measured by F-ratio or KNN classification performance. In contrast, no such invariance properties are observed for the unsupervised networks. Although F-ratio of the bottleneck-versions of the AEN and DBN increases during the reconstruction of the input, the activations are not more informative regarding the corresponding phone identity as revealed by decreasing KNN performance. With a fixed or expanding number of nodes in the hidden layers (Table 1), very minor improvements in phone selectivity (max. 2.7%) are observed in comparison to input features but without any abstraction from gender-specific patterns.

In addition, the MI between individual node activations and phone labels is not positively correlated with the discriminability of the overall pattern of activation across all nodes–not even in the supervised case (Figs. 2 and 3). A closer analysis of the distributions of node-specific MI-values in case of the MLP revealed that the MIs become more tightly concentrated towards small values with an increasing layer number. Simultaneously, the number of highly informative individual nodes decreases. This suggests that the representations at higher layers are inherently distributed and the same nodes contribute to encoding of multiple different phone classes. When analyzed individually, each node will naturally show increased selectivity towards an internally coherent subset of all possible speech inputs, but this should not be confused with overall capability of the individual nodes to represent abstracted categorical knowledge.

In order to ensure that the results were not affected by overfitting of the model to the data, we also conducted the same set of analyses for the activations on the training data. No qualitative differences were observed in the results in this case. In addition, we re-ran the experiments using a shorter input window length (5 frames ≈ 50 ms) to ensure that the phonemic structure was not lost due to the inclusion of the neighboring temporal context in the acoustic representations during the training stage. Again, the results were qualitatively similar to those reported with a longer input window.

Finally, since the KNN performance was always higher for a BP-fine-tuned autoencoder in comparison to the pre-training only, we also ran further 100 iterations of the BP-algorithm to see whether the KNN performance of the AEN layers would increase above the original input Mel-spectrum selectivity with the help of extra training. However, the KNN-based selectivity measure flattened out around the level observed in Figs. 2 and 3 and then started to decrease with more training epochs, likely due to overfitting.

Overall, it seems that the DBN is simply smoothing the input data (lower KNN-performance and more uniform activations in terms of F-ratio at deeper layers) whereas fine-tuning of the AEN leads to low-dimensional but detailed representations that encode both suprasegmental and segmental acoustic details. Unlike the supervised MLP, neither the DBN nor AEN exhibit increased phonemic invariance in comparison to the original input features.

Discussion and conclusions

The present experiments investigated the emergence of phonemic representations in unsupervised deep neural networks using adult-directed speech from multiple talkers similarly to the supervised counterpart performed earlier (Nagamine et al., 2015) and on single-talker data of child-directed speech. The central finding is that the studied deep feedforward networks did not show similar increased selectivity towards phonemic structure that was observed in the networks trained in a supervised manner (Nagamine et al., 2015) or in the auditory neurons of the superior temporal gyrus as analyzed by Mesgarani et al. (2014).

The results are also qualitatively different from the earlier clustering studies that have reported above-chance grouping of acoustic spectra or formants frequencies to disjoint phone-like categories (e.g., de Boer & Kuhl, 2003; Vallabha et al., 2007; Kouki et al., 2010). However, a major difference to the earlier clustering studies is that the DNNs do not force division of the data samples into a finite number of categories similarly to standard clustering algorithms, but learn distributed representations of the statistical structure of the data. In addition, our input data to the learning process was not carefully chosen to represent stable parts of vowel sounds but contained continuously extracted slices of the speech input – a situation that the auditory system has to also face unless further temporal constraints such as syllabic (Räsänen, Frank & Doyle, 2015) or phonetic (e.g., Räsänen, 2014) boundary cues are included in the process. This leaves open whether the phonemic structure in DNNs would become more explicit under more constrained but ecologically plausible learning settings. Another possibility is that the use of recurrent neural network architectures could learn better context-dependent models for speech patterns as they do not assume independence of the neighboring speech frames similarly to the currently studied networks. Although such units would conflict with the idea of a phone or phoneme as a context-independent cluster of spectral properties, a simplification often assumed in early language acquisition research, it is well known that human speech perception also operates on longer time-spans than individual segments.

Results from the supervised paradigm clearly indicate that the selectivity of the internal representations become more phonemic when the target output is also phonemic in nature. In the context of modeling early language acquisition, the targets cannot be discrete phone labels as such. However, the precise labels could be substituted to other available and correlating information such as larger structural units the input frames belong to (e.g., Elsner et al., 2012; Feldman et al., 2013; Synnaeve et al., 2014) or even the cross-situational referential context in which the speech is observed (Räsänen & Rasilo, 2015). This could lead to similar, albeit slower, learning of representations showing phonemic invariance.

Interestingly, despite the absence of increased phonemic invariance in the unsupervised networks, the findings should still be compatible with the basic idea of distributional adaptation to the native language phonetic system (e.g., Kuhl et al., 2008) since the studied networks learn a generative statistical model over the training input. The input speech reconstructions from the network will depend on the familiarity with the input and are biased towards the statistical patterns of the training data. As long as the perceptual representations for speech input are assumed to correspond to the activations of the hidden layers or the reconstruction itself, the system is less sensitive to phonetic details of “non-native” speech patterns the more it is trained with one language only. This provides an analogy between human distributional learning and overfitting of statistical models to a certain set of training data. However, computational verification and implications of this idea are out of the scope of the present study and should be addressed in the future work.