Unraveling submicron-scale mechanical heterogeneity by three-dimensional X-ray microdiffraction

Significance

Shear bands critically control the strength and ductility in a wide range of structural, geological, and biological materials. The nondestructive three-dimensional structural probing of individual shear bands has hitherto not been possible for investigation at the critical mesoscopic length scales. The X-ray microdiffraction study reported in this work reveals the highly localized stress gradients and microscopic damage mechanisms across the fatigue shear bands. The resulting local strain gradients lead to severe stress concentrations at the submicrometer scale, causing an anomalous deviation of the classical Coffin−Manson rule for the high-cycle fatigue failure of metals. This work opens an avenue for harnessing the synchrotron-based, 3D spatially resolved X-ray for studying the heterogeneous deformation and fracture in bulk materials.

Abstract

Shear banding is a ubiquitous phenomenon of severe plastic deformation, and damage accumulation in shear bands often results in the catastrophic failure of a material. Despite extensive studies, the microscopic mechanisms of strain localization and deformation damage in shear bands remain elusive due to their spatial−temporal complexities embedded in bulk materials. Here we conducted synchrotron-based X-ray microdiffraction (μXRD) experiments to map out the 3D lattice strain field with a submicron resolution around fatigue shear bands in a stainless steel. Both in situ and postmortem μXRD results revealed large lattice strain gradients at intersections of the primary and secondary shear bands. Such strain gradients resulted in severe mechanical heterogeneities across the fatigue shear bands, leading to reduced fatigue limits in the high-cycle regime. The ability to spatially quantify the localized strain gradients with submicron resolution through μXRD opens opportunities for understanding the microscopic mechanisms of damage and failure in bulk materials.

Shear bands are the narrow layers of materials undergoing intense shearing strains. They usually form during severe plastic deformation of ductile materials (1). Damage accumulation and resulting instabilities in shear bands represent one of the most common modes of material failure. Under a high strain rate load, shear banding is exacerbated by local adiabatic heating, thereby triggering a catastrophic material failure. This has been demonstrated with the fast punching of steel by Zener and Holloman (2) in the 1940s. In contrast, under a slow monotonic or cyclic load, cumulative damage is gradually developed within the microscale shear bands such as dislocation slip bands, leading to the eventual material failure. In their fatigue experiments, Mughrabi and coworkers (3, 4) made pioneering studies of the striking formation of persistent slip bands in wavy slip metals in the 1980s. A similar shear banding phenomenon of formation of persistent Lüders bands was observed by Laird and coworkers (5) and others (6, 7) in planar slip alloys experiencing fatigue deformation. However, the spatial−temporal complexities associated with shear bands during cyclic loading pose substantial challenges to a clear understanding of fatigue damage mechanisms (8), which is essential to the prevention of fatigue failure. To overcome these challenges, it is necessary to develop in situ spatially resolved techniques for mapping the local deformations within and around shear bands.

A variety of experimental techniques has been employed to probe the localized deformation and damage accumulation in the shear bands. Postmortem transmission electron microscopy (TEM) experiments reveal a rich spectrum of phenomena associated with the dislocation microstructures in crystalline metals and alloys. However, there is a critical lack of related in situ experiments. As such, one natural question is whether or not the mechanisms extracted from a postmortem TEM experiment truly play a dominant role in the real deformation process. In this regard, we note that recent progress of in situ TEM techniques (9, 10) has enabled a real-time visualization of dynamic deformation processes associated with the microscopic defects such as dislocations, grain boundaries, and phase boundaries, etc. However, TEM imaging requires the use of thin-foil samples. As a result, the dominant defect processes in TEM experiments could be strongly influenced by the free surfaces nearby, such that they could differ qualitatively with those in bulk samples. On the other hand, in situ X-ray diffraction experiments are able to capture the real-time microscopic deformation processes in bulk samples under both monotonic and cycling loadings (11–13). However, they are often limited by low spatial resolution. Therefore, there is currently a critical need for novel experimental techniques for in situ spatially resolved characterization of the microscopic deformation and damage processes in bulk samples (14, 15).

Experiments

Here we employed a 3D synchrotron X-ray microdiffraction (3D μXRD) technique to investigate the strain localization and damage accumulation in fatigue shear bands. Our 3D μXRD experiments were performed at the Advanced Photon Source (APS) in Argonne National Laboratory. Spatially resolved diffraction measurements were conducted by using differential aperture X-ray microscopy (16) at the beamline 34-ID-E of APS. A polychromatic or monochromatic X-ray microbeam was focused by a pair of the Kirkpatrick−Baez mirrors to a small spot of 0.5 μm by 0.5 μm, where the Laue diffraction patterns were recorded on a PerkinElmer area detector. The depth resolution was provided by a 100-μm-diameter platinum wire as a diffracted beam profiler (differential aperture) scanning along the incident beam on the specimen surface during measurements. A crystal orientation map was obtained in the polychromatic mode with an accuracy of 0.01°, while the absolute lattice parameters and hence local elastic lattice strains inside individual grains were quantitatively measured in the monochromatic energy-scanning mode with an accuracy of 10⁻⁴. Hence a high spatial resolution of measurement is achieved at the submicrometer level in all three dimensions (17, 18). With recent development of depth profiling in the fly-scan mode for high-speed data collection, together with a higher X-ray beam flux provided by more advanced mirror focusing optics, large sample volume mapping becomes routinely practical for in situ experiments.

An austenite stainless steel with a composition of 24 wt % nickel, 20 wt % chromium, 6.2 wt % molybdenum, and 0.22 wt % nitrogen, commonly referred to as AL6XN (SI Appendix, Fig. S1), was used in our experiments. This material is known to have a low stacking fault energy. As a result, planar slip prevails, yielding a characteristic network of planar slip bands during fatigue cycling. The 3D μXRD technique used in this work (SI Appendix, Fig. S2) enables the mapping of both crystal orientations and lattice strains in bulk materials with a high spatial resolution at the submicrometer scale, superior to other techniques such as electron backscatter diffraction (EBSD) (19) and neutron diffraction (20). Our work is focused on mapping the lattice strain field in samples after high-cycle (low-strain) fatigue tests. That is, we used the fatigued samples that had underwent 29,000 load cycles with a controlled amplitude of 0.3% and strain ratio of R = −1 (corresponding to ∼75% of the fatigue life of AL6XN stainless steel). The fatigue sample was cut into a dog-bone-shaped tensile specimen, with an effective gauge dimension of 2.75 mm in length, 1.25 mm in width, and 0.2 mm in thickness. This specimen was first characterized by ex situ 3D μXRD without loading and then by in situ 3D μXRD under a 0.5% tensile strain load applied along the same direction as fatigue testing.

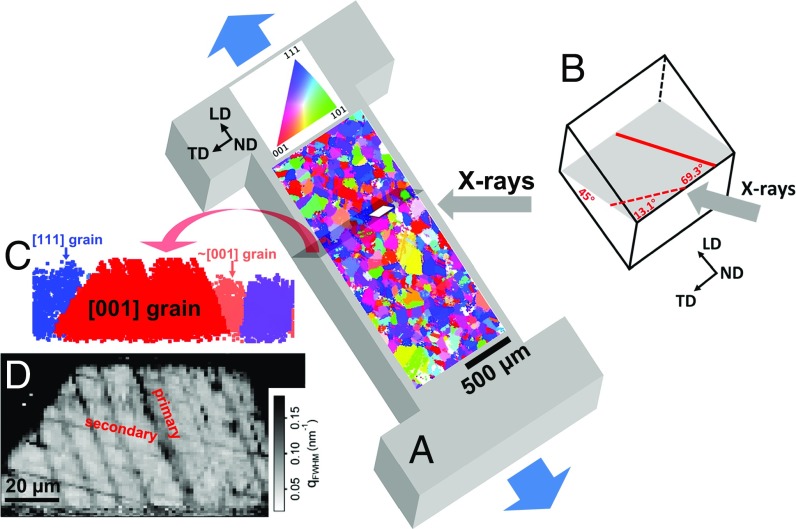
Fig. 1A shows the schematic of the specimen cut from a fatigued sample. Superimposed on the specimen surface is a crystal orientation map of near-surface grains measured by μXRD. The orientation of the incident X-ray beam in relation to the sample geometry is schematically shown in Fig. 1B. Grains in the specimen have an average size of ∼100 microns with random orientations. Fig. 1C shows an orientation map of an inclined cross-section of the specimen, slicing along the X-ray beam direction. A grain with its [001] axis along the loading direction (LD) is colored in red and hereafter referred to as the [001] grain. This grain is located in between one [111] grain (colored in blue) and one grain (colored in brown) with ∼20° deviation from [001]. The Schmidt factors of the primary slip system in these three grains are 0.430, 0.353, and 0.493, respectively. To investigate the deformation microstructure inside the [001] grain, Bragg reflection (480) was used to probe the local lattice strains, ε_ND, along the surface normal direction (ND) of the specimen. As shown in Fig. 1D, a map of the peak full width at half maximum (FWHM) of the diffraction vector q was obtained [where q = |q| = (4π/λ) sinθ, λ is the X-ray wavelength, and θ is the Bragg angle]. The magnitude of FWHM represents the average density of stored dislocations and/or other defects in the detected crystal volume (21). Through the gray scale contrast in the map, a network of shear bands, with the band widths ranging from ∼1 μm to 5 μm, is clearly seen inside the [001] grain. These shear bands are, in fact, the dislocation slip bands as they coincide with the primary and secondary dislocation slip planes activated during fatigue testing (as indicated by solid and dashed lines, respectively, in the X-ray slicing plane in Fig. 1B and SI Appendix, Fig. S4). Grains with other orientations (e.g., [110] grains) were also examined, but no obvious band structure was found (SI Appendix, Fig. S3). This indicates that the [001] grain is the “soft” grain in the sample that facilitates shear banding and damage accumulation during high-cycle fatigue testing with the low strain amplitude.

Fig. 1.

Experimental setup and results of in situ μXRD testing. (A) Schematic of a tensile specimen cut from a fatigued sample of stainless steel. The specimen is covered with a crystal orientation map of near-surface grains from μXRD measurement. The map is colored by the LD inverse pole figure, with the color scheme shown in the orientation triangle. (B) Schematic of an incident X-ray slicing plane (in gray) at 45° to the sample surface. The specimen orientations are represented in terms of the LD, surface ND, and TD. The primary and secondary shear bands in the map are respectively represented by the solid and dashed lines. (C) A crystal orientation map slicing along the X-ray beam direction, measured with polychromatic X-rays. The [001]//LD grain is colored in red. (D) A map of the (480) diffraction peak FWHM of the same [001] grain shown in C, measured with monochromatic X-ray. The primary and secondary shear bands, as marked in the map, can be readily identified according to the gray scale. All of the measurements have the spatial resolution of ∼1 μm in three dimensions.

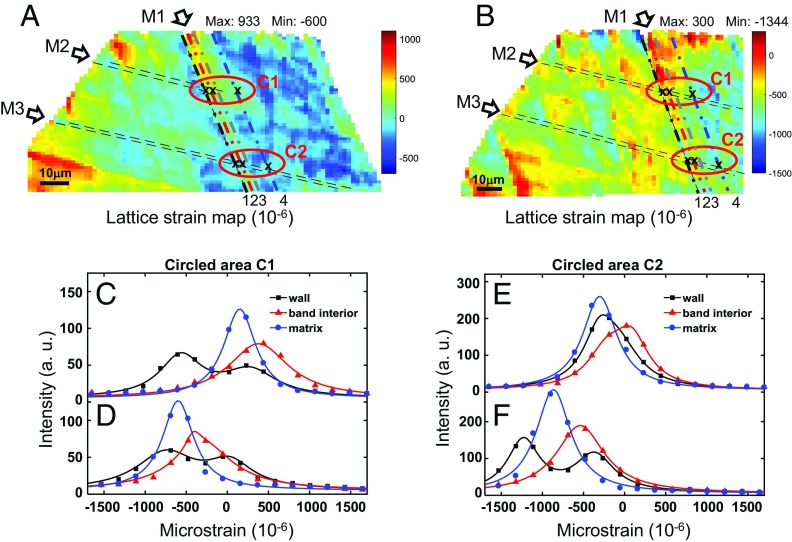
Fig. 2A shows a map of lattice strains (ε_ND) along ND in the [001] grain. Large tensile and compressive strains prevailed in the left and right portion of the grain, respectively. Given an applied tensile strain along LD, the strains along ND would be uniformly compressive in an unconstrained grain, as dictated by Poisson’s effect. However, the tensile strains dominated in the left portion of the [001] grain, reaching the maximum of about 900 µε (where 1 µε represents a strain of 10⁻⁶). Such large local strains overrode the applied strain, indicating a large local incompatibility of deformation near the grain boundary between adjoining [001] and [111] grains. Similarly, the dominant compressive strains in the right portion of the [001] grain arose due to a large deformation incompatibility near the local grain boundary.

Fig. 2.

Lattice strain distributions in the [001]//LD grain before and after applying a tensile strain of 0.5%. All of the lattice strains are measured in the surface ND of the specimen. (A) The (480) lattice strain map before tensile loading. The primary shear band is labeled as M1, while the two secondary shear bands are labeled as M2 and M3. The wall of the primary shear band is marked by line 1, band interior is marked by line 2, diffuse band wall is marked by line 3, and grain matrix is marked by line 4. (B) Same as A except after tensile loading. (C and D) Diffraction profiles near the intersecting zone (C1) between M1 and M2 bands, before and after loading at the band wall, band interior, and matrix. (E and F) Same as C and D but near the intersecting zone (C2) between M1 and M3 bands.

Importantly, Fig. 2A shows the highly heterogeneous lattice strains near the intersections of shear bands within the [001] grain, as highlighted by circles (marked by C1 and C2). Recall that individual shear bands can be clearly recognized in the FWHM map of Fig. 1D. With reference to Fig. 1D, we focused our analysis on a broad primary shear band (labeled as M1) in Fig. 2A. This band had a width of about 4 μm (captured by a few X-ray measurement pixels). Through a detailed analysis of FWHM and lattice misorientation (to be shown in Fig. 3), we identified a sharp wall of the M1 band (marked by line 1), the band interior (line 2), another diffuse wall of the band (line 3), and the grain matrix away from the band (line 4). The sharp wall is associated with a low-energy dislocation structure (22, 23), while the diffuse wall is related to the distributed dislocations, to be shown by TEM image later. Fig. 2C shows the intensity profiles of the diffraction vector q representing the local lattice strains near intersections of the M1 band and a fine secondary shear band (labeled as M2). Importantly, the split diffraction peaks within a measurement pixel (as shown by the black curve) were observed near the sharp wall of the M1 band. The two diffraction peaks occurred respectively at a tensile strain of 275 µε and a compressive strain of 565 µε along ND. This sharp transition from the tensile to compressive lattice strain within a measurement pixel (∼0.5 μm in size) indicates a large local strain gradient at the submicron scale, which suggests a strong local interaction between the primary and secondary shear bands. The corresponding local stress gradient was estimated as ∼163 MPa, using the elastic modulus (∼194 GPa) along the [110] slip direction in stainless steel (24). Such a large local stress gradient represents a severe mechanical heterogeneity that could markedly accelerate fatigue damage. In contrast, single diffraction peaks were measured inside both the band interior and the matrix, suggesting smaller strain gradients therein. However, the diffraction peak in the band interior is broader than that in the matrix, implying a higher density of dislocations in the former than the latter.

Fig. 3.

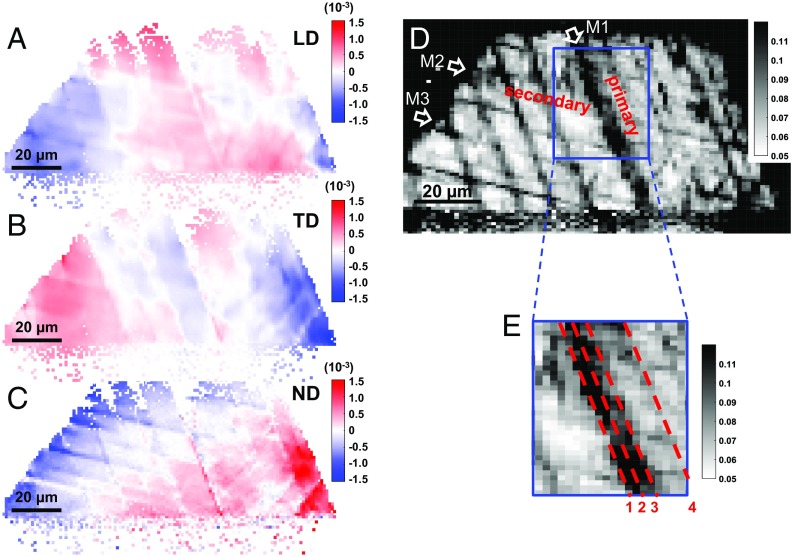
Analysis of lattice orientation and diffraction peak in the [001]//LD grain. (A–C) Maps of lattice orientation showing grain subdivision due to the formation of shear bands; these maps are colored based on the components of the Rodrigues vector along LD, TD, and ND, respectively. The mean values of the three components for the whole grain are centered on zero. The unit of color bars in A–C is radian. (D) Map of the (480) diffraction peak FWHM, q_FWHM (same as Fig. 1D)_, showing the fine structure of the primary slip band M1. (E) A magnified region at the M1 band in D; the wall of the primary shear band M1 is marked by line 1, band interior is marked by line 2, diffuse band wall is marked by line 3, and grain matrix is marked by line 4.

After the above postmortem μXRD mapping, in situ μXRD testing was performed by applying a tensile load to the specimen. When the applied tensile strain along LD was increased by 0.5%, the distribution of lattice strains in the [001] grain changed considerably (Fig. 2B). Due to Poisson’s effect, the applied tensile strain resulted in substantial lateral contraction. As shown in Fig. 2B, lattice strains along ND were reduced in both the matrix and the shear band interior. Comparing Fig. 2 C and D, all diffraction peaks were shifted toward less tensile or more compressive strains. For example, the shift of the diffraction peak in the matrix reflects a strain decrease of about 790 µε along ND. To a first approximation, we assumed a uniform change of stress in the [001] grain and thus estimated a stress decrease by ∼247 MPa along LD, using the elastic modulus (∼94 GPa) in the [001] direction of LD and Poisson’s ratio of 0.3 in stainless steel (24). This estimate is close to the macroscopic change of stress ∼270 MPa in the specimen at 0.5% engineering strain. In contrast, the shifts of the two split diffraction peaks in the sharp wall were relatively small, giving a strain decrease of only about 230 µε. This indicates that it is difficult to rearrange local dislocation structures associated with large strain gradients. Nonetheless, the change of local lattice strain gradients provides direct evidence of dynamic interactions between the primary and secondary shear bands (23). More detailed dynamic evolution of strain gradients can be tracked from the μXRD lattice strain maps before and after loading near the M1 band (SI Appendix, Fig. S5).

Comparison of Fig. 2 A and B also reveals a different mode of dynamic evolution of large local strain gradients, which occurs near an intersection between the primary shear band M1 and a fine secondary shear band M3. Fig. 2 E and F shows the corresponding diffraction profiles collected at the sharp wall (line 1), the band interior (line 2), and the grain matrix (line 4) before and after a 0.5% increment of the applied tensile strain along LD. In contrast to Fig. 2 C and D, the diffraction peak split was initially absent (Fig. 2E), but emerged at the wall (black line) only after applying a large tensile strain load of 0.5% (Fig. 2F). The corresponding maximum compressive strain reached about −1,400 µε in ND. This implied that a large local strain gradient could result from a sudden load change during fatigue cycling. Such strain gradient could arise due to the formation of a major dislocation configuration, e.g., an array of edge dislocations of the same sign rearranged near the intersection of the two shear bands. Hence, these in situ μXRD measurements directly reveal the dynamic formation of a large local strain gradient resulting from interactions between the primary and secondary shear bands.

The rich information on the crystal rotations can be clearly captured through tracing the distribution of local lattice orientations presented in the Rodrigues space. Grain subdivision due to the formation of fatigue shear bands in the [001] grain can be characterized by fine misorientation mapping in three directions, i.e., LD, transverse direction (TD) and ND, of the Rodrigues space, as shown in Fig. 3 A–C. Evidently, the lattice orientation varies from the left to right part of the [001] grain, but spans a small range of ∼0.8°, as dictated by the local strain compatibilities of neighboring grains. Interestingly, a relatively large gradient in local lattice orientation at the left boundaries (line 1) of the M1 band is observed, and it is characterized by a sharp contrast in misorientation varying from 0.04° to 0.10° across the shear band wall. In principle, the observed sharp wall structure of the M1 band can be understood in terms of a low-angle grain boundary model, where the associated array of geometrically necessary dislocations is responsible for the misorientation detected by μXRD. This finding is consistent with the orientation jumps across slip bands, as revealed in a previous study using high-resolution EBSD (25). It should be noticed that the resolution in orientation space by μXRD is one magnitude higher than that by EBSD. It can also be seen from the orientation map that there are almost no appreciable gradients of lattice orientations across the secondary slip bands such as M2 and M3 bands. In addition, Fig. 3 D and E shows a detailed analysis of the FWHM map through correlation with the orientation map, so as to highlight the fine features of the primary slip band M1. Specifically, we used two criteria, i.e., FWHM and misorientation, to identify the sharp wall (line 1), band interior (line 2), and diffuse wall (line 3) in Fig. 3E. If there is an obvious gradient in both FWHM and orientation, the sharp wall is identified. If there is a gradient in FWHM but no obvious gradient in orientation, the diffuse wall is defined. Between the two walls, the band interior features the high values of FWHM, but involves no obvious gradient in both orientation and FWHM.

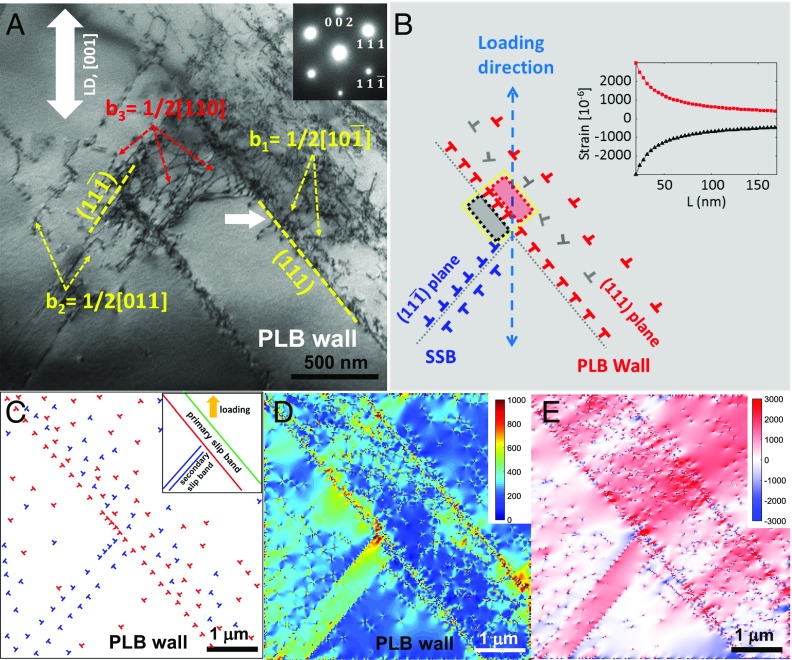
To understand the origin of large local strain gradients revealed by μXRD, we performed TEM observations of dislocation structures around the primary and secondary shear bands in a [001] grain (Fig. 4A), selected from the same fatigued specimen. The broad primary shear band with the typical widths of 0.5 μm to 2 µm consists of a planar array of dislocations (marked by an arrow) corresponding to a sharp wall of the band. This type of band is commonly referred to as the persistent Lüders band. Inside the band are rafts of dislocation dipoles and multipoles laying on the (111) slip planes. The formation of complex rafts is likely associated with the operation of dislocations on multiple slip systems within the primary shear bands. In contrast, the fine secondary shear bands consist of dipolar dislocation arrays on the ($11\overline{1}$) slip planes. They are inferred from the diffraction peak broadening (Fig. 1D), and also from the fact that almost no appreciable gradients were measured by 3D μXRD in both orientations and lattice strains across secondary shear bands (as shown in Figs. 2A and 3 A–C). The fine secondary shear bands intersect the broad primary shear bands, but cannot penetrate into the latter. This is evidenced by an abrupt jump of lattice strain from the matrix (around line 4) to the primary shear band (around line 1) in the μXRD map (Fig. 2A and SI Appendix, Fig. S6). From a double-beam TEM analysis, we determined the Burgers vector of dislocations as b₁ = 1/2 [$10\overline{1}$] on the primary (111) slip plane and b₂ = 1/2 [011] on the secondary ($11\overline{1}$) slip plane (Fig. 4A). The sessile Lomer−Cottrell locks, with the Burgers vector b₃ = 1/2 [110] on the (001) planes, formed according to the dislocation reaction of 1/2 [$10\overline{1}$] + 1/2 [011] = 1/2 [110] (Fig. 4A). These sessile locks act as strong obstacles to dislocation glide under further loading (22, 26). Dislocation structures near the intersection between the primary and secondary slip bands are schematically shown in Fig. 4B. In the boxed area, a large local tensile stress arises due to the pileup of edge dislocations of the same sign and prevails on the side of the dislocation pileup with “missing” half atomic planes. Meanwhile, a large local compressive stress arises on the other side of the pileup with “extra” half atomic planes. The calculated tensile and compressive strains as a function of mean spacing of dislocations in the pileup are plotted in Fig. 4B, Inset, and SI Appendix, Fig. S6. Based on the measured strain gradient and associated stress gradient of ∼163 MPa at the intersection of M1 and M2 bands, we estimated the mean dislocation spacing in the pileup as about 100 nm and the length of the pileup as no less than 10 μm. Hence, there are about 100 edge dislocations of the same sign in the dislocation pileup at the “wall” of the primary shear band.

Fig. 4.

TEM image and dislocation dynamic simulations of dislocation structures in an [001] grain. (A) Bright-field TEM image viewed along the [110] zone axis (with the electron diffraction pattern displayed in the Inset), showing dislocation structures in the (111) primary slip band and the ($11\overline{1}$) secondary slip band (SSB). The (111) primary slip band consists of a sharp wall of a planar array of dislocations with the same sign, and hence this band is marked as a persistent Lüders band (PLB). (B) Analysis of the large local strain gradient developed the intersection of the two slip bands. Inset shows the calculated local strain gradient in the boxed region; the tensile strain at the red box and the compressive stress at the black box are calculated as a function of dislocation spacing, L, in the dislocation pileup array representing a sharp wall of a PLB. (C) Relaxed dislocation configuration from a 2D dislocation dynamics simulation of interactions between dislocations in the primary and secondary slip bands (as schematically shown in Inset). (D and E) Contour of (D) von Mises stress and (E) lattice strain along the q vector of [120], which are calculated from the relaxed dislocation configuration in C. To a first approximation, two conjugate slip systems are assumed to be activated during cyclic loading in the simulation; the dislocation configuration and associated stress/strain field were obtained through unloading and thus relaxing the applied load. The applied shear stress in the simulation cell, elastic modulus, and Poisson’s ratio are taken as 100 MPa, 190 GPa, and 0.3, respectively.

Simulations

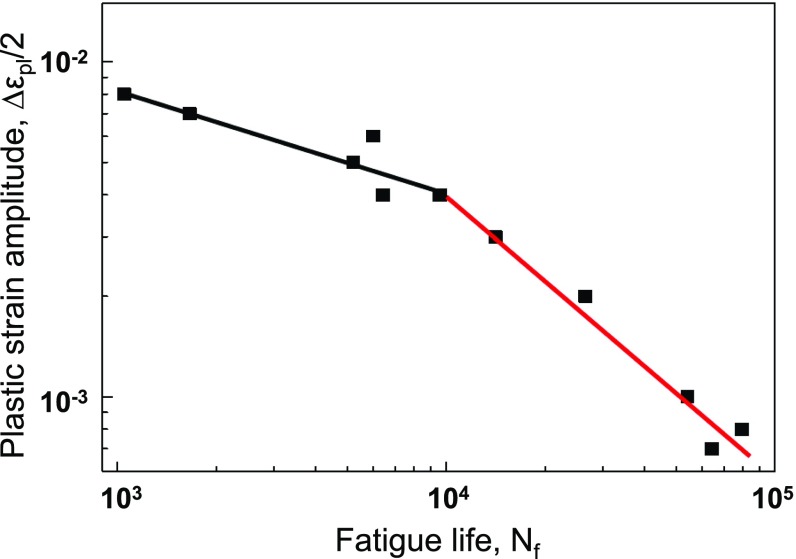
To directly reveal the mechanical heterogeneity associated with the large local stress gradient from the analysis in Experiments, we performed a 2D dislocation dynamics simulation (27) of interaction between the primary and secondary slip systems. Based on the μXRD and TEM results, we constructed a primary shear band that consists of a planar array of pileup dislocations with the same sign, giving a sharp wall of the persistent Lüders band. From the above stress gradient analysis, the mean dislocation spacing in this array was set as 100 nm. In addition, dislocations were randomly distributed in the band interior and matrix, giving a diffuse wall of the band. Based on μXRD measurements, the density of these random dislocations in the band interior and matrix was set as 4 × 10¹⁴ m⁻² and 1 × 10¹⁴ m⁻², respectively. We also constructed a secondary shear band that consists of two dislocation pileup arrays with the opposite sign of the Burgers vector. The two arrays have a close spacing of about 0.5 μm. This secondary shear band was obstructed by the primary shear band. The detailed geometries of slip systems and materials parameters are described in SI Appendix and associated SI Appendix, Fig. S7. Fig. 4C shows the relaxed dislocation configuration after applying three stress cycles at the far field. The resulting distributions of von Mises stress and elastic strain along the q vector of [120] are plotted in Fig. 4 D and E. Evidently, a large stress concentration arises where the two shear bands intersect, with a local stress gradient of 174 MPa over an X-ray pixel size of about 0.5 µm that is close to the corresponding experimental value of 163 MPa. This local stress concentration leads to a severe mechanical heterogeneity that can accelerate fatigue damage and thus result in fatigue failure. Indeed, the prevalent formation of shear bands in the “soft” [001] grains from our μXRD and TEM observations correlates with the attainment of fatigue life limit (corresponding to the red-line limit in Fig. 5) during our high-cycle fatigue tests of stainless steel. Hence, we consider the mechanical heterogeneity associated with large local strain gradients across fatigue shear bands to be responsible for the damage failure that leads to a deviation in Fig. 5 from the classical Coffin−Manson rule, i.e., a single linear relationship in the double-logarithmic plot of plastic strain amplitude $\mathrm{\Delta }{\epsilon }_{\text{pl}}/2$ versus cycle number to failure N_f (28).

Fig. 5.

Experimentally measured results (symbols) of plastic strain amplitude ($\mathrm{\Delta }{\mathit{\epsilon }}_{\mathbf{p}\mathbf{l}}/2$) against fatigue cycle to failure (N_f) for the Al6XN stainless steel, showing a deviation from the classical Coffin−Manson rule (i.e., a single linear curve in a double logarithmic plot). The solid lines are the fitting curves.

Conclusions

Our μXRD experiments mapped out the 3D lattice strain field with submicron resolution across the fatigue shear bands in large sample volumes of stainless steel. The μXRD results revealed the large, local lattice strain gradients across the shear bands. Such strain localization results in the severe mechanical heterogeneities that can accelerate fatigue damage and lead to fatigue failure. Experimental findings of these localized strain and stress gradients are essential for understanding the damage mechanisms underpinning the shear band instabilities and material failure. As demonstrated in this work, spatially resolved in situ 3D μXRD mapping at the submicron scale provides an opportunity for unraveling the microscopic damage and failure mechanisms in plastically deformed bulk materials.