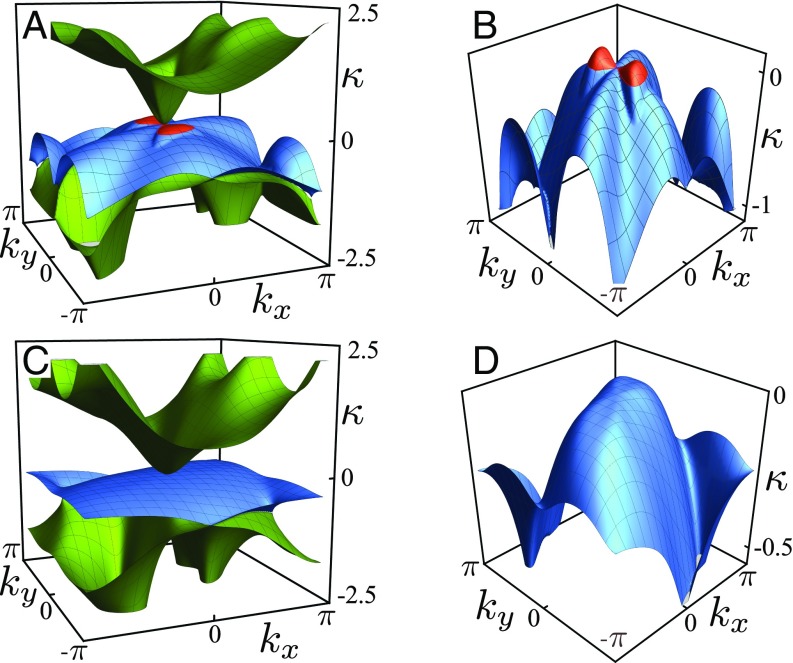
Fig. 3.

Surface modes for a polarized lattice (C and D) compared with a lattice with Weyl lines (A and B). A surface mode in a plane perpendicular to the $z$ axis (e.g., Fig. 1C) decays exponentially into the material bulk with amplitude $e^{-\kappa z/|{\text{𝒂}}_3|}$, where $\kappa$ is the inverse penetration depth. Lattice with Weyl lines $(\varphi ,\theta ,\psi )=(5\pi /12,\mathrm{\hspace{0.17em}0},\pi /4)$. (A) Inverse penetration depth for three soft surface modes over the entire surface Brillouin zone (sBZ). For small wave vectors $(k_x,k_y)$, these modes correspond to the three acoustic phonons. (B) Zoomed in view of the middle mode in A: the part of wave vector space for which the mode lives on the bottom side is colored in red, whereas the part corresponding to the top side is in blue. The projection of the Weyl line from the bulk onto the sBZ corresponds to a line with infinite penetration depth ($\kappa =\mathrm{\hspace{0.17em}0}$) and separates the red and blue regions. Polarized lattice $(\varphi ,\theta ,\psi )=(\pi /3,\mathrm{\hspace{0.17em}0},\pi /3)$. (C) Inverse penetration depth for the same three modes as in A but for a different choice of parameters, corresponding to the blue region in Fig. 2A. (D) Zoomed in view of the middle mode in C, which (in contrast to the mode in B) is localized on the top of the lattice only: it is blue throughout. Significantly, the bulk ($\kappa =\mathrm{\hspace{0.17em}0}$) modes that correspond to the Weyl loop are absent for this lattice.