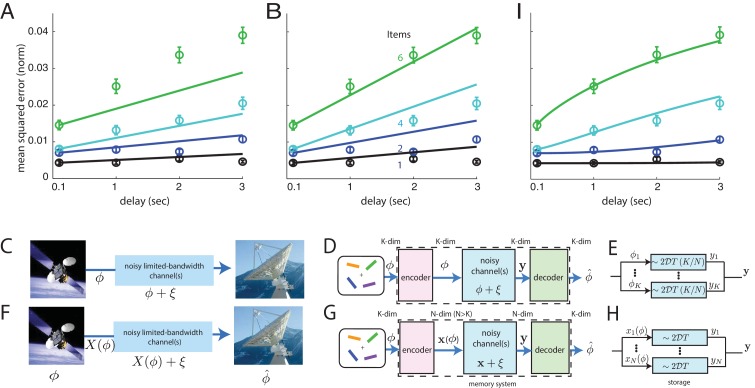
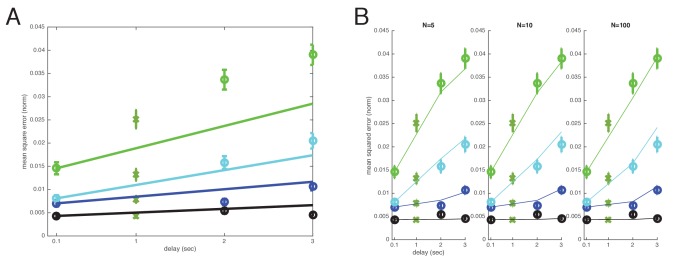
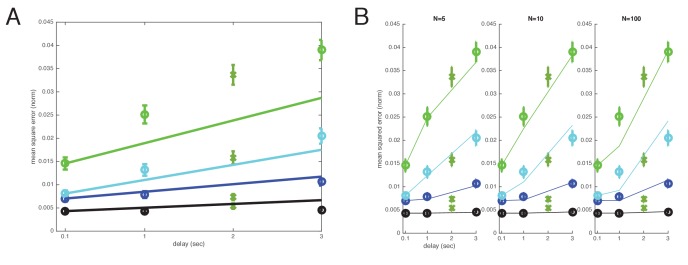
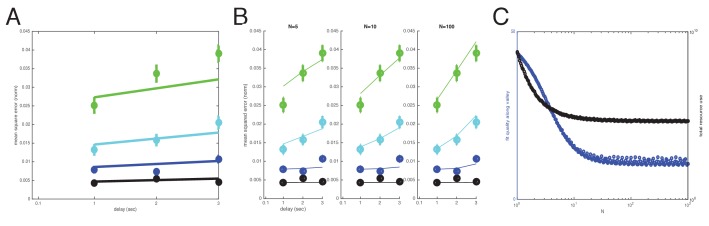
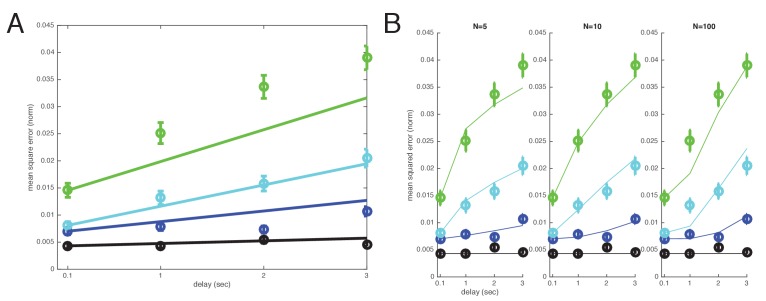
Figure 3. Comparison of direct and coded storage models using persistent activity networks with human memory performance.

(A) Lines: predictions from the direct storage model for human memory. The theory specifies all curves with a single free parameter, after shifting each curve to the measured value of performance at the shortest delay interval of 100 ms. Fits performed by weighted least squares (weights are inverse SEM). (B) Similar to (A), but parameters fit by ordinary least-squares to only the 6-item curve; note the discrepancy in the 1- and 2-item fits. (C–E) Information ($\varphi$) is directly transmitted (or stored) in a noisy channel, and at the end an estimate of $\widehat{\varphi }$ of $\varphi$ is recovered. (C) A scenario involving space-to-earth communication. (D) The scenario for direct storage in noisy memory banks (the nosy channels); the encoder and decoder are simply the identity transformation in the case of direct storage and hence do nothing. (E) The $K$ pieces of information in the $K$-dimensional vector $\varphi$ are each represented in one of $K$ continuous attractor neural networks of size $N\mathrm{/}K$ neurons each. Each attractor representation accumulates squared error linearly over time and inversely with $N\mathrm{/}K$. (F–H) Same as (C–E), but here information is first encoded ($\varphi \mathrm{\to }\mathbf{𝐗}\mathrm{}\mathrm{\left(}\varphi \mathrm{\right)}$) with appropriate structure and redundancy to combat the channel noise. A good encoder-decoder pair can return an estimate $\widehat{\varphi }$ that has lower error than the direct strategy, even with similar resource use, mitigating the effects of channel noise for high-fidelity information preservation. (H) The $K$-dimensional $\mathit{\varphi }$ is encoded as the ($N$-dimensional) codeword $\mathbf{𝐱}$, each entry of which is stored in one of $N$ persistent activity networks. Squared error in the channel grows linearly with time as before; however, the resources used to build $K$ channels of quality $\mathrm{\left(}N\mathrm{/}K\mathrm{\right)}\mathrm{}\mathrm{1}\mathrm{/}\mathrm{2}\mathrm{}𝒟$ from before are redirected into building $N$ channels of poorer quality $\mathrm{1}\mathrm{/}\mathrm{2}\mathrm{}𝒟$ (assuming $N\mathrm{>}K$). The decoder estimates $\mathit{\varphi }$ from $N$-dimensional output $\mathbf{𝐲}$. (I) Same as (A), but the model lines are the lower-bound on mean-squared error obtained from an information-theoretic model of memory with good coding. (Model fit by weighted least-squares; the theory specifies all curves with two free parameters, after shifting each curve to the measured value of performance at the shortest delay interval of 100 ms).

Figure 3—figure supplement 1. Cross-validated comparison of the direct and well-coded storage models after leaving out $T\mathrm{=}\mathrm{1}$s datapoints.

The A) direct and B) well-coded storage models are fit to the data, excluding the datapoints at time ($T\mathrm{=}\mathrm{1}$s). This is a leave-one-out or jackknife cross-validation procedure. The well-coded model predicts the withheld datapoints with smaller error than the uncoded/direct coding model. Direct model: Sum of weighted least-squares error (WLS error): 103.3984; sum of squares error: 0.022888; squared error on held-out $T\mathrm{=}\mathrm{1000}$ ms point: 0.0043414. Well-coded model (with minimum error near $N\mathrm{=}\mathrm{10}$): WLS error: 11.3172; sum of squares error: 0.0016302; squared error on held-out $T\mathrm{=}\mathrm{1000}$ ms point: 0.0011631. BIC score: Delta BIC = BIC(direct model all items WLS) - BIC(coded model all items WLS): 11.4039, in favor of the well-coded model.

Figure 3—figure supplement 2. Cross-validated comparison of the direct and well-coded storage models after leaving out $T\mathrm{=}\mathrm{2}$s datapoints.

The A) direct and B) well-coded storage models are fit to the data, excluding the datapoints at time ($T\mathrm{=}\mathrm{2}$s). This is a leave-one-out or jackknife cross-validation procedure. The well-coded model predicts the withheld datapoints with smaller error than the uncoded/direct coding model. Direct model: WLS error: 79.2137; sum of squares error: 0.015975; squared error on held-out $T\mathrm{=}\mathrm{2000}$ ms point: 0.010418. Well-coded model (with minimum error near $N\mathrm{=}\mathrm{5}$): WLS error: 2.9575; sum of squares error: 0.0007505; squared error on held-out $T\mathrm{=}\mathrm{2000}$ ms point: 0.00083856. BIC scores: Delta BIC = BIC(direct model all items WLS) - BIC(coded model all items WLS): 32.4666, in favor of well-coded model.

Figure 3—figure supplement 3. Comparison of models after removal of the shortest (100 ms) delay time-point under the argument that it represents a different memory process (iconic memory).

The $T\mathrm{=}\mathrm{1000}$ ms point is now used as the baseline level to analyze the time degradation of stored memory, instead of the $T\mathrm{=}\mathrm{100}$ ms point, which is deleted altogether from the analysis. The argument for this analysis is that $T\mathrm{=}\mathrm{100}$ms might overlap with the process of iconic memory and should not be used in a comparison across the longer-latency short-term memory interval datapoints. The (A) direct model and (B) well-coded model, where (C) fit-quality plateaus to a nearly asymptotic constant with increasing $N$ (but the asymptotic value is nearly achieved by $N\mathrm{=}\mathrm{10}$). Direct model: WLS error: 37.317; sum of squares error: 0.0080949. Well-coded model (no minimum in error in interior of range; asymptotic decay of error with $N$, with near-asymptotic value reached by $N\mathrm{=}\mathrm{10}$; here, we use $N\mathrm{=}\mathrm{100}$, but similar results including BIC scores for $N\mathrm{=}\mathrm{10}$: WLS error: 12.493; sum of squares error: 0.0019871. Delta BIC = BIC(direct model all items WLS) - BIC(coded model all items WLS): 24.8239, in favor of the well-coded model.

Figure 3—figure supplement 4. Redefining item numbers as $K\mathrm{=}\mathrm{\left[}\mathrm{1\hspace{0.25em}4\hspace{0.25em}8\hspace{0.25em}12}\mathrm{\right]}$ (instead of $K\mathrm{=}\mathrm{\left[}\mathrm{1\hspace{0.25em}2\hspace{0.25em}4\hspace{0.25em}6}\mathrm{\right]}$) to take into account the memorization of item color in addition to orientation.

1. Fits with direct storage model and (B) well-coded model. For the well-coded model, fit quality reaches a minimum around N = 10. Direct model: WLS error: 80.4649; sum of squares error: 0.016218. Well-coded model (with minimum error near $N\mathrm{=}\mathrm{10}$): WLS error: 12.4617; sum of squares error: 0.0016035. Delta BIC = BIC(direct model all items WLS) - BIC(coded model all items WLS): 68.0032 in favor of the coded model.