Fig. 2.

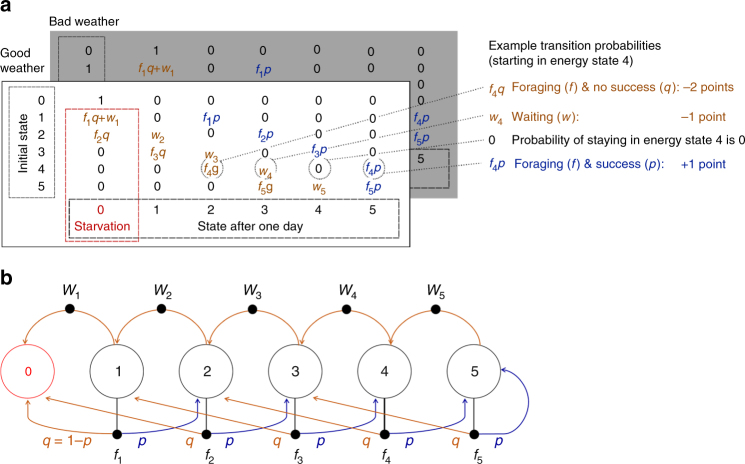
Markov decision process underlying the sequential decision-making task. a Example transition matrices used for determining the value differences between the two choice options according to the optimal policy (corresponding to the forest in Fig. 1). The entries in the matrices are the probabilities to transition from the initial energy state (rows) to the final energy state (columns) in one step. These entries (and their positions within the matrix) depend on the weather types of the forests and on the choice patterns. Many of the entries are 0, which means that transitions between the respective initial and final states are impossible. The forest is specified by the probability of foraging success p (with q = 1−p) and the magnitude of gains and losses. These magnitudes are reflected in the positions of the probabilities within the matrix. Choices are reflected by the probabilities for foraging f and waiting w (with f = 1−w). The probabilities f and w depend on the initial state and are indexed accordingly. Additionally, the optimal policy depends on the number of remaining days in the forest since there is a finite horizon with a maximum number of five days. Starvation is absorbing, which is why the probability of staying in state zero is 1. There are two corresponding transition matrices for the two weather types. Backward computation is used to determine the value differences between the two choice options according to the optimal policies. That is, the values of the two choice options are first evaluated according to the last day in the forest, then according to the second-last day, etc. b The state transition diagram (for one weather type) corresponding to the example transition matrix in a. Large circles depict (energy) states and small filled circles depict the two actions to choose from. Arrows indicate transitions between states. For clarity, only one weather type is shown. In total, each forest type comprises 12 states = 6 (energy states) × 2 (weather types)