Abstract
Plaque morphology and biomechanics are believed to be closely associated with plaque progression. In this paper, we test the hypothesis that integrating morphological and biomechanical risk factors would result in better predictive power for plaque progression prediction. A sample size of 374 intravascular ultrasound (IVUS) slices was obtained from 9 patients with IVUS follow-up data. 3D fluid-structure interaction models were constructed to obtain both structural stress/strain and fluid biomechanical conditions. Data for eight morphological and biomechanical risk factors were extracted for each slice. Plaque area increase (PAI) and wall thickness increase (WTI) were chosen as two measures for plaque progression. Progression measure and risk factors were fed to generalized linear mixed models and linear mixed-effect models to perform prediction and correlation analysis, respectively. All combinations of eight risk factors were exhausted to identify the optimal predictor(s) with highest prediction accuracy defined as sum of sensitivity and specificity. When using a single risk factor, plaque wall stress (PWS) at baseline was the best predictor for plaque progression (PAI and WTI). The optimal predictor among all possible combinations for PAI was PWS + PWSn + Lipid percent + Min cap thickness + Plaque Area (PA) + Plaque Burden (PB) (prediction accuracy=1.5928) while Wall Thickness (WT) + Plaque Wall Strain (PWSn) + Plaque Area (PA) was the best for WTI (1.2589). This indicated that PAI was a more predictable measure than WTI. The combination including both morphological and biomechanical parameters had improved prediction accuracy, compared to predictions using only morphological features.
Keywords: Coronary, Fluid, structure interaction, Plaque progression, IVUS, Follow-up study
1. Introduction
Atherosclerotic plaque progression and rupture involve complex biological, biochemical, biomechanical and pathological processes, etc. (Stary et al., 1995; Virmani et al., 2000; Ku et al., 1985; Tang et al. 2009). The pioneering works of Fry, Caro, Ku, Giddens, Friedman and Malek, among others, showed that initiation of atherosclerosis process correlates positively with low and oscillating flow shear stress (Fry et al., 1968; Caro et al., 1971, Ku et al., 1985; Giddens et al., 1993; Friedman et al., 1987; Malek et al., 1999). However, the mechanism governing advanced plaque progression has not been fully understood (Tang et al., 2014). Loree et al., Ohayon et al., Gijsen et al., our group and other groups have conducted studies on assessing plaque vulnerability from both biomechanical and morphological perspectives for coronary and carotid arteries (Loree et al., 1992; Ohayon et al., 2008; Wang et al. 2015a; Gijsen et al., 2015). Glagov et al. investigated coronary vessel enlargement and lumen narrowing processes occurring in coronaries during plaque growth using histological human coronary sections from 136 hearts (Glagov et al., 1987). It should be noted that most of the earlier studies were based on one-time plaque data, while plaque progression needs to be quantified using patient follow-up data (at least two observations).
Several groups have made great effort to find the potential indicator to predict the plaque development over time. Results from the PROSPECT study (n=697) showed that nonculprit lesions associated with recurrent events were more likely to have plaque burden of 70% or greater than those not associated with recurrent events (p<0.001) (Stone GW et al., 2011). From the PREDICTION study, Stone PH et al. concluded that progressive plaque enlargement and lumen narrowing could be predicted independently by baseline large plaque burden and low endothelial shear stress (Stone PH et al., 2012). In an IVUS-based follow-up study with 20 patients recruited, Samady et al. divided IVUS slices into low, intermediate and high wall shear stress (WSS) groups. They reported that the low-WSS group developed significant progression in plaque area and necrotic core, whereas the high-WSS group had progression of necrotic core but regression of fibrous and fibro-fatty tissue (Samady et al., 2011). Following a similar method, Corban et al. found that the group with baseline plaque burden >40% and WSS <10 dyn/cm2 had significantly greater change in plaque area at follow-up (0.68±1.05 mm2), compared to the group with plaque burden >40% and WSS >10dyn/cm2 (Corban et al., 2014). Using a multi-level modeling approach, Sakellarios et al. claimed endothelial shear stress and low-density lipoprotein had a significant correlation with the changes in plaque area, therefore these factors had the potential to predict the regions that are prone to plaque progression (Sakellarios et al., 2017). Most of the studies in the literature (with a few exceptions) focused on flow shear stress and did not take the effect of structural mechanical conditions on plaque development into consideration (Maurice RL et al., 2004). For this reason, our group has published preliminary results on plaque progression using wall thickness and the mechanical conditions from the fluid-structure interaction (FSI) models (Wang et al, 2015b). Even though most existing studies focus on the relationship between plaque progression and morphological features, we conjecture that integrating all possible risk factors including morphological and biomechanical factors from plaque structure and blood flow would result in better predictive power for plaque progression prediction.
In this paper, follow-up intravascular ultrasound (IVUS) coronary plaque data were acquired from 9 patients and IVUS-based FSI models with cyclic bending were constructed to obtain data for eight selected key plaque morphological and biomechanical parameters including wall thickness (WT), plaque wall stress (PWS), plaque wall strain (PWSn), wall shear stress (WSS), lipid percent, min cap thickness, plaque area (PA) and plaque burden (PB). All possible combinations of these risk factors were fed into generalized linear mixed models (GLMM) to predict plaque progression in two measures: wall thickness increase (WTI), plaque area increase (PAI). All possible combinations were tested to identify the optimal predictor with highest prediction accuracy defined as the sum of prediction sensitivity and specificity for each measure. Correlation analyses were performed between plaque progression and risk factors using linear mixed-effect models (LME).
2. Data, Method and Model
2.1. Data acquisition and processing
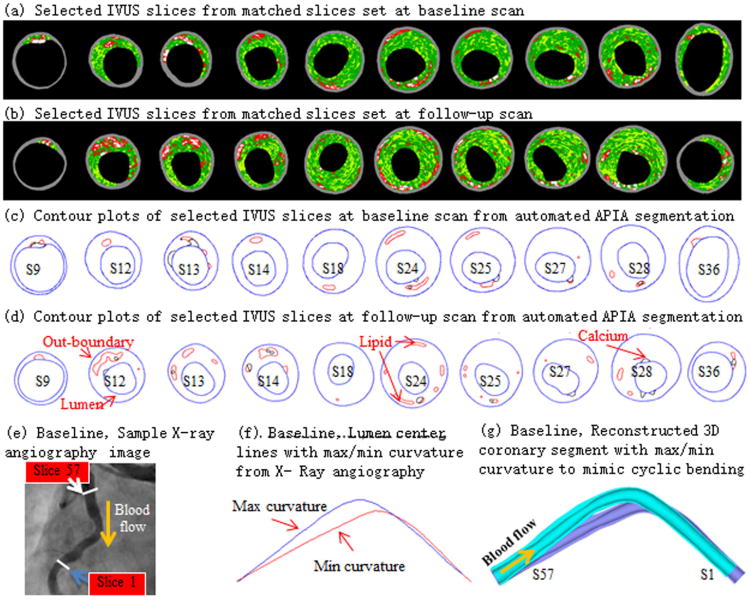
IVUS with virtual histology (IVUS-VH) coronary plaque data were acquired from 9 patients (Mean age: 59, 7 males) with one-time follow-up (follow-up time span 6-12 months, median 9 months) at Cardiovascular Research Foundation (New York, NY) with informed consent obtained (the PROSPECT study, Stone GW et at., 2011). Patient demographical information are provided by Table 1. Data acquisition procedures were described previously in (Wang et al. 2015a, 2015b). X-ray angiogram (Allura Xper FD10 System, Philips, Bothel, WA) was obtained at both scans to show the location of the coronary artery stenosis, vessel curvature and cyclic bending caused by heart contraction. VH-IVUS data provides maps of lipid, calcification, and fibrotic tissues. Fusion of IVUS data and X-ray angiography to reconstruct 3D blood vessel geometry were performed after the segmentation and co-registration of the one-by-one paired slices at baseline and follow-up using information from angiography, location of myocardium, vessel bifurcation, stenosis and plaque components following established procedures (Wang et al, 2015b). Figure 1 gives one sample with selected registered IVUS-VH images and segmented contours at baseline and follow-up, angiography, and vessel sagittal view with maximum and minimum curvatures demonstrating cyclic bending.
Table 1. Patient demographical and related general conditions (BP = Blood Pressure).
| Patient ID | Age | Gender | BP (mmHg) | Follow-up time (month) | Weight (kg) | Height (cm) | BMI | Diagnosis History | Total Choles terol | Trigly-cerides | Smo ke | Culprit Vessels |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 51.6 | Male | 60-135 | 6 | 84 | 153 | 35.88 | Stable Angina | NA | NA | Yes | RCA |
| P2 | 71.3 | Male | 70-125 | 12 | 79 | 173 | 26.39 | None | 194 | 272 | No | LCx |
| P3 | 67.5 | Male | 70-120 | 9 | 73 | 170 | 25.26 | Stable Angina | 181 | 142 | No | RCA |
| P4 | 52.0 | Male | 73-113 | 8 | 95.26 | 178 | 30.06 | None | 210 | 168 | Yes | RCA, LCx |
| P5 | 42.7 | Female | 66-110 | 12 | 86.64 | 175 | 28.21 | None | 203 | 131 | Yes | RCA, LAD |
| P6 | 48.4 | Male | 91-153 | 9 | 136.5 | 183 | 40.82 | Stable Angina | 187 | 165 | Yes | LAD |
| P7 | 71.6 | Male | 95-171 | 12 | 109 | 178 | 34.40 | Unknown | 132 | 153 | No | LAD |
| P8 | 76.0 | Female | 44-120 | 6 | 53 | 159 | 20.96 | Unstable Angina | 130 | NA | No | LAD |
| P9 | 49.1 | Male | 76-134 | 6 | 100 | 172 | 33.80 | Unstable Angina | 188 | 123 | Yes | LAD, LCx |
Figure 1.
(a)-(d) Matched IVUS-VH and segmented contour plots of sliced from baseline scan and follow-up scan. (e) Sample frame from X-ray Angiography movie to show min curvature at baseline. (f)-(g) Max and min curvatures were extracted to reconstruct coronary segment in 3D to mimic its cyclic bending movement due to heart contraction at Baseline.
2.2. The fluid-structure interaction (FSI) model
In vivo IVUS-based 3D FSI models with anisotropic material properties and pre-shrink-stretch process were constructed for each coronary plaque to obtain plaque stress, strain and flow wall shear stress conditions. Blood flow was assumed to be laminar, Newtonian (Yang et al., 2007; Kari et al., 2017), and incompressible. The Navier-Stokes equations with arbitrary Lagrangian-Eulerian (ALE) formulation were used as the governing equations. The structure model included equilibrium equations (equation of motion), the nonlinear Cauchy-Green strain-displacement relation and Mooney-Rivlin material properties. Pulsating pressure conditions were prescribed at the inlet and outlet of the vessel. No-slip boundary conditions were imposed on the fluid-vessel interface. Other boundary conditions were prescribed to the appropriate interfaces to recover the physiological conditions and cyclic bending movement of coronary (Yang et al., 2009).
2.3 The Mooney-Rivlin material model
The vessel tissue was assumed to be hyperelastic, anisotropic, nearly-incompressible and homogeneous. Plaque components (lipid core and calcification) were assumed to be hyperelasic, isotropic, nearly-incompressible. A modified Mooney-Rivlin material model was used to describe the material properties of vessel tissue with the strain energy density function given below (Holzapfel et al., 2000):
| (1) |
| (2) |
| (3) |
| (4) |
where I1 and I2 are the first and second invariants of right Cauchy-Green deformation tensor C defined as C=[Cij] = XTX, X=[Xij] = [∂xi/∂aj], (xi) is current position, (ai) is original position, I4 = Cij(nc)i(nc)j, nc is the unit vector in the circumferential direction of the vessel, c1, c2, D1, D2, and K1 and K2 are material constants determined by fitting the biaxial testing experimental data using a two-step square-least method. The parameters for the vessel (fibrous tissue) used in this paper were: c1= -1312.9 kPa, c2=114.7 kPa, D1=629.7 kPa, D2=2.0, K1=35.9 kPa, K2=23.5. The parameters used for lipid and calcification are: Lipid: c1= 0.5 kPa, c2=0 kPa, D1=0.5 kPa, D2=1.5; Ca: c1= 92 kPa, c2=0 kPa, D1=36 kPa, D2=2.0. Material parameters were used in our previous publications and are also consistent with data available in the literature (Holzapfel et al., 2000; Kural et al., 2012; Yang et al., 2009; Teng et al., 2014).
2.4. Mesh construction and solution method
Patient-specific plaque models were constructed at both baseline and follow-up and solved by ADINA (Adina R&D, Watertown, MA) to obtain mechanical conditions including plaque wall stress (PWS), plaque wall strain (PWSn) and wall shear stress (WSS) (Bathe et al., 2002). Details about our pre-shrink-stretch model construction process and component-fitting mesh generation technique can be found in (Yang et al., 2009).
2.5 Data extraction for morphological and biomechanical factors
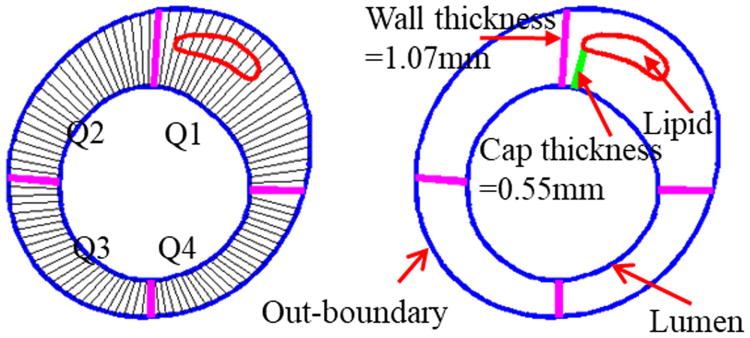
Three hundred and seventy-four IVUS slices from 9 patients (baseline and follow-up matched) were used to extract data for morphological and biomechanical factors for analyses. Each slice was divided into 4 quarters with each quarter containing 25 evenly-spaced nodal points on the lumen, each lumen nodal point was connected to a corresponding point on vessel outer-boundary. The length of the connecting line is defined as the wall thickness at the nodal point. Cap thickness at a lumen point is the shortest distance between the lumen point and lipid contour the cap is covering. The minimum of the cap thickness (wall thickness if the connecting line does not pass lipid) among the 100 nodal points was denoted as the min cap thickness of the slice. Figure 2 gives a sketch of the definitions of these morphological features. The area of lipid within each slice was recorded as lipid area. Plaque area (PA) is defined as the area between lumen and out-boundary. Plaque burden (PB) is given by:
Figure 2.
Sketch explaining definitions of quarters, wall thickness, cap thickness, and lipid.
| (5) |
Lipid percent for each slice was also calculated:
| (6) |
Average values of PWS, PWSn and WSS over 100 nodal points for each slice were calculated and used in our analyses. Data for the eight morphological and biomechanical risk factors including WT, PWS, PWSn, WSS, Lipid percent, Min cap thickness, PA and PB were obtained for the 374 slices for statistical analysis.
2.6 Plaque Progression Measurement
Vessel wall thickness increase (WTI) and plaque area increase (PAI) from baseline to follow-up were chosen as two measures for plaque progression:
| (7) |
| (8) |
2.7 Linear mixed-effect (LME) model for correlation analysis
A linear mixed-effect (LME) model was used to study the correlation between plaque progression (i.e., WTI/PAI) and each risk factor with data dependence structure taken into consideration (Wu et al., 2011). The LME model is given by:
| (9) |
where Yjk, xjk are the observational data of plaque progression and any risk factor at baseline on the jth slice in the kth patient. β0, β1 are the coefficients for the fixed-effect term, bk is the random effect term and εjk is the vector of random error term. LME considers a sophisticated dependence structure among the observational data since WTI/PAI or risk factors acquired from two slices within the same patient model are unlikely independent. Similar to Pearson's correlation coefficient, the dependence-adjusted correlation coefficient r was defined by:
| (10) |
where and are the sample variances of the risk factor and plaque progression.
2.8 Generalized linear mixed models (GLMM) for prediction analysis
Generalized linear mixed models (GLMM) for binary responses were used to select the best predictor(s) for each measure of plaque progression. We use WTI as an example to explain our GLMM model training and testing process. The same analysis could be applied to PAI. For a given slice, we set the binary response WTI=1 if WTI>0 or WTI=0 if WTI<=0. The GLMM model is given by (Wu et al., 2011):
| (11) |
| (12) |
where yjk is the binary response of WTI on the jth slice of the kth patient. The expectation of yjk is the probability: E(yjk|bk) = P(yjk = 1|bk) and the binomial link function is: . And x1, x2, etc. in GLMMs presents the combinations of risk factors at baseline as predictor. The terms β0, β1, bk, εjk have the same meaning in LME models and were estimated by fitting GLMM using R function glmmPQL (Venables et al., 2002).
A 5-fold cross-validation procedure was performed as all 374 IVUS slices were randomly split into five subgroups with four training subgroups to fit the model and the remaining one as validation subgroup to evaluate the model. Prediction specificity and sensitivity are defined as the proportion of slices in the validation subgroup that correctly identified as WTI=1 class and WTI=0 class, respectively. All combinations of eight risk factors were tested to identify the optimal predictor with the highest prediction accuracy defined as the sum of specificity and sensitivity. The receiver operating characteristic curve (ROC curve) and the area under of the ROC curve (AUC) were reported to compare the prediction accuracy for each combination. It is worth noting that sensitivity and specificity reported for each predictor were determined from the point on the ROC curve that gives their highest sum.
3. Results
3.1. Correlation analysis between risk factors and WTI
Table 2 shows correlation results between the eight risk factors and plaque progression measured by WTI using 374 slices. Using the baseline data, WT showed the strongest significant correlation with WTI (r= - 0.7962, p=6.32E-33), followed by PA (r=-0.7399, p=1.22E-11). Except for these two risk factors, PB and WSS also correlated with WTI negatively. There are no significant correlations observed between WTI and the rest of 4 risk factors.
Table 2. Correlation results between WTI and eight risk factors at baseline and follow-up. NS=No statistical significance.
| WTI vs. | ||||
|---|---|---|---|---|
| Risk factor | baseline | follow-up | ||
| r | p | r | p | |
| WT | -0.7962 | 6.32E-33 | 0.9309 | 1.93E-50 |
| PWS | 0.0371 | 0.5853(NS) | -0.1596 | 0.0020 |
| PWSn | 0.0552 | 0.3338(NS) | -0.2023 | 9.49E-05 |
| WSS | -0.2639 | 0.0004 | 0.5784 | 2.67E- 12 |
| Lipid percent | 0.0007 | 0.9884(NS) | 0.1009 | 0.1263(NS) |
| Min cap thickness | 0.0437 | 0.1955(NS) | 0.0433 | 0.2876(NS) |
| PA | -0.7399 | 1.22E-11 | 0.9152 | 1.40E-31 |
| PB | -0.5985 | 1.08E-15 | 0.8176 | 1.01E-32 |
When fitting LME with follow-up data, most of the correlations changed sign from baseline. WT had the strongest positive correlation with WTI. PWS and PWSn at follow-up became negatively associated with WTI from no significant correlation at baseline.
3.2 Prediction of WTI by eight risk factors
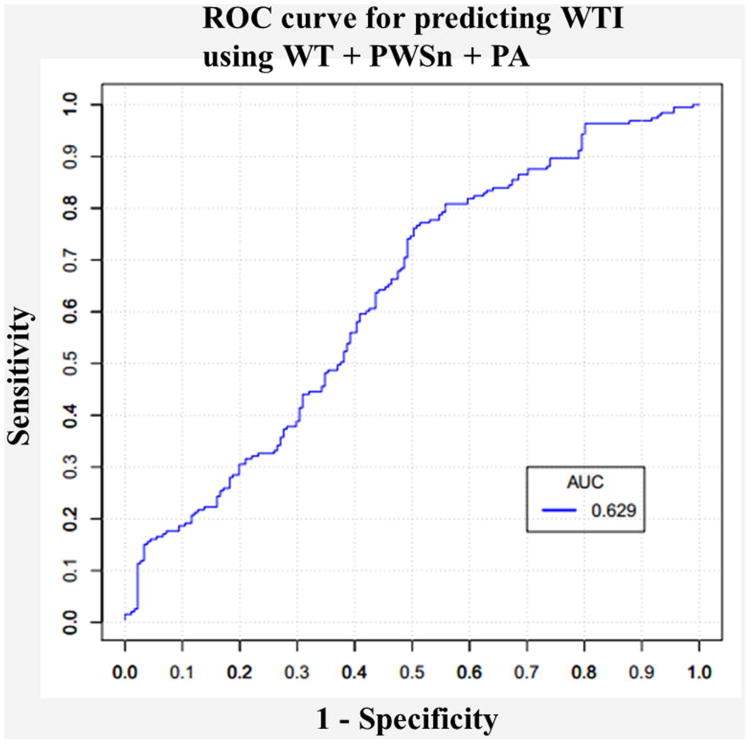
There are altogether 255 (2̂8-1) combinations using the eight risk factors. Table 3 gives the prediction results for WTI using single risk factors at baseline, and the optimal combination predictor among all 255 combinations. It showed that PWS was the best single risk factor predictor for WT1 with highest sum of sensitivity and specificity (1.2205), followed by PWSn (1.1802). When comparing all possible combinations of the eight risk factors, the combination of WT, PWSn and PA gave the best prediction accuracy 1.2589. Figure 3 shows the ROC curve and AUC value for predicting WTI using the optimal predictor WT, PWSn and PA at baseline.
Table 3. WTI prediction sensitivity and specificity, AUC value of WTI using single risk factor and the optimal combination among all 255 combinations.
| Predictor | Prob Cutoffs | Sensitivity | Specificity | Sensi+Speci | AUC |
|---|---|---|---|---|---|
| WT+PWSn+PA | 0.4987 | 0.7617 | 0.4972 | 1.2589 | 0.6289 |
| PWS | 0.5246 | 0.5907 | 0.6298 | 1.2205 | 0.6250 |
| PWSn | 0.4958 | 0.7668 | 0.4144 | 1.1812 | 0.6046 |
| PB | 0.4186 | 0.9482 | 0.2210 | 1.1692 | 0.5938 |
| Lipid percent | 0.5031 | 0.7772 | 0.3867 | 1.1639 | 0.6024 |
| PA | 0.4404 | 0.8964 | 0.2652 | 1.1616 | 0.5789 |
| WSS | 0.4481 | 0.8601 | 0.2873 | 1.1474 | 0.5773 |
| WT | 0.4522 | 0.8756 | 0.2707 | 1.1463 | 0.5948 |
| Min cap thickness | 0.3646 | 0.9637 | 0.1823 | 1.1460 | 0.5816 |
Figure 3.
Receiver operating characteristic (ROC) curve and area under curve (AUC) value using WT + PWSn + PA to predict WTI.
3.3. Correlation analysis between risk factors and PAI
According to Table 4, PA, WT and PB at baseline are the 3 morphological features that had strong negative correlations with PAI, with PA giving highest correlation coefficient r = - 0.8330. For the other two morphological features at baseline, min cap thickness showed weak correlation while lipid percent had no significant correlation. All 3 mechanical conditions at baseline showed no statistically significant correlation with PAI.
Table 4. Correlation results between PAI and eight risk factors at baseline and follow-up.
| PAI vs. | ||||
|---|---|---|---|---|
| Risk factor | baseline | follow-up | ||
| r | p | r | p | |
| WT | -0.5262 | 1.48E-13 | 0.9929 | 6.35E-36 |
| PWS | 0.0185 | 0.7338(NS) | -0.0683 | 0.0890(NS) |
| PWSn | 0.0377 | 0.4064(NS) | -0.0894 | 0.0266 |
| WSS | -0.1128 | 0.0673(NS) | 0.3179 | 1.76E-06 |
| Lipid percent | 0.0043 | 0.9031(NS) | 0.0903 | 0.0826(NS) |
| Min cap thickness | 0.0560 | 0.0320 | 0.0152 | 0.6253(NS) |
| PA | -0.8330 | 6.89E-26 | 0.9890 | 4.58E-49 |
| PB | -0.4678 | 4.87E-13 | 0.9610 | 1.20E-28 |
At follow-up, PA, WT and PB were still the risk factors giving strong correlation coefficients, but now they had positive significant correlation with PAI. For mechanical conditions, PWSn and WSS showed weak correlations with PAI while PWS showed no significant correlation.
3.4. Prediction of PAI by eight risk factors
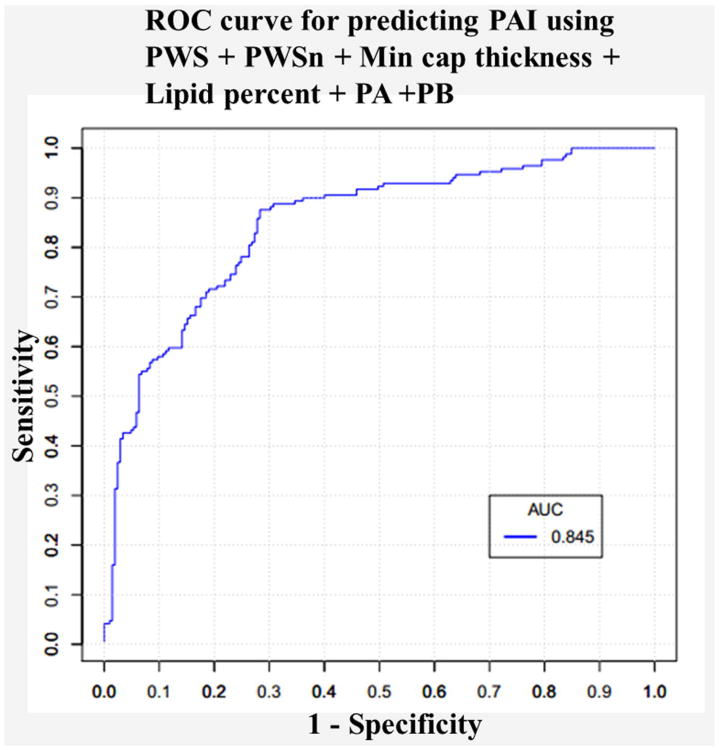
Similar to WTI prediction, the prediction results for single risk factors at baseline, along with the optimal combination predictor are summarized by Table 5. PWS was the best single risk factor predictor for PAI with the highest sum of sensitivity and specificity (1.4856) with AUC=0.8116, followed by PB (1.4849) with AUC=0.7996. The combination of PWS, PWSn, Lipid percent, min cap thickness, PA and PB gave the best prediction accuracy (1.5928), with AUC=0.8452. The ROC curve and AUC value for best predictor are given in Figure 4.
Table 5. Prediction sensitivity and specificity, AUC value of PAI using one single risk factor and optimal predictor among all combinations.
| Predictor | ProbCutoffs | Sensitivity | Specificity | Sensi+Speci | AUC |
|---|---|---|---|---|---|
| PWS+PWSn+Lipid percent+Min cap thickness+PA+PB | 0.3810 | 0.8757 | 0.7171 | 1.5928 | 0.8452 |
| PWS | 0.4348 | 0.7929 | 0.6927 | 1.4856 | 0.8116 |
| PB | 0.5680 | 0.6508 | 0.8341 | 1.4849 | 0.7996 |
| WSS | 0.3527 | 0.8521 | 0.6244 | 1.4765 | 0.7896 |
| PWSn | 0.4964 | 0.7041 | 0.7366 | 1.4407 | 0.7740 |
| Lipid percent | 0.4193 | 0.8402 | 0.6000 | 1.4402 | 0.7749 |
| WT | 0.4509 | 0.7751 | 0.6634 | 1.4385 | 0.7576 |
| Min cap thickness | 0.3001 | 0.9467 | 0.4634 | 1.4101 | 0.7661 |
| PA | 0.3830 | 0.7988 | 0.6049 | 1.4037 | 0.7579 |
Figure 4.
Receiver operating characteristic (ROC) curve and area of the curve from predicting PAI using PWS + PWSn + Lipid percent + Min cap thickness + PA + PB.
4. Discussion
4.1 Combining morphological factors, structural stress/strain and flow shear stress for plaque progression prediction
Most prior and current plaque progression research focused on plaque morphological and fluid flow risk factors (Stone et al., 2012; Samady et al., 2011).Little attention has been paid to structural plaque stress and strain (PWS and PWSn), partially due to availability of plaque data with components and the time cost and modeling complexity in calculating these mechanical conditions. However, structural stress/strain should play an important role here. By using IVUS-VH data with follow-up, we were able to construct multi-component coronary plaque FSI models and perform progression prediction using five morphological and three mechanical risk factors. Our preliminary results indicate that combining morphological and mechanical factors could give better prediction accuracy for plaque progression. We also demonstrated that PWS was the best single risk factor among the eight morphological and mechanical factors for predicting PAI and WTI, the two chosen measures for plaque progression in this paper. These findings supports further effort and investigations in this direction.
4.2 PAI is more predictable than WTI as a measure for plaque progression
Plaque area (PA) and wall thickness (WT) are two commonly used measures to size atherosclerotic plaque prevalence in coronary or carotid artery. Naturally, we used PAI and WTI to assess plaque progression and compared their differences. Using the eight risk factors at baseline as predictors, our results indicate that PAI was more predictable than WTI, with the combinations of PWS + PWSn + Lipid percent + Min cap thickness + PA + PB achieving a prediction accuracy 1.5928 and AUC value (0.8452). A sensitivity of 0.8757 and specificity of 0.7171 showed this predictor had reasonably good ability to indicate how PA would change. At least 71% of slices could get correct agreement between predicted and realistic plaque size change regardless of how it changes. In comparison, the optimal predictor for WTI can only achieve a prediction accuracy 1.2589. This may suggest that we may want to adopt PAI for plaque progression investigations in the future.
4.3 Correlation between vessel enlargement and lumen area
Glagov et al. used histological coronary data from 136 human cadaver hearts to study correlation between vessel enlargement and plaque area. They reported that the internal elastic lamina area correlated with the area of the lesion (r=0.44, P< 0.001) (Glagov et al., 1987). Using data from our 374 IVUS slices, it was found that the Pearson's correlation coefficients between plaque area and internal elastic lamina area were r=0.5777, p-value<0.0001 at baseline and r=0.4769, p-value<0.0001 at follow-up. This is consistent with Glagov's finding.
4.4 Limitations on VH-IVUS data and modeling process
(a) IVUS has a limited resolution of 150-250 microns and cannot detect thin plaque cap with cap thickness around 65 microns.. Sometimes, the lipid-rich necrotic core (lipid core) from IVUS-VH even sits on the lumen. To our best effort, we made cap with thickness about 50 microns (slightly smaller than 65 microns threshold value for thin cap) when IVUS-VH data had lipid-rich core on the lumen (Wang et al., 2015b). (b) Patient-specific vessel and plaque component material properties were not available for this study. Material parameter values in our models were chosen from our ex vivo biaxial test data and available literature (Guo et al., 2017); (c) One major limitation in the modeling procedure is the lack of biplane angiography to re-construct vessel curvature in 3D. Our patient data were acquired with only one angiography image data. Care was taken to find the angiography with maximum curvature variations of the vessel segment of interest. (d) Micro-calcifications were not included in the current FSI model due to limitations of imaging (Bluestein et al., 2008); (e) IVUS data do not contain the adventitial layer of the vessel. Our results should be understood and interpreted with that assumption; (f) Residual stress was not included as no patient-specific opening angle data were available (Fung et al., 1995; Ohayon et al., 2007); (g) Interaction between the heart and vessel were not considered (Ohayon et al., 2011). A model coupling heart motion and coronary bending would be desirable when required data become available.
4.5 Future directions for improvement
Future research and investigation could be done to address the following issues to make this work more complete, enhance the results or overcome the limitations: a) Efforts in more accurate calculation of the mechanical conditions should be made such as considering residual stress and biplane angiography into the computational FSI models; b) Another potential improvement is to combine IVUS-VH and OCT (resolution 15-20 microns) for more precise information on plaque morphology. OCT has a resolution 15-20 microns, therefore it can visualize thin cap thickness as complementary to IVUS; c) Attempts to automate FSI modeling procedures are called for to make large-scale studies feasible. Even though patient-specific FSI models are time-consuming and complicated, structural mechanical conditions are demonstrated to be essential risk factors for plaque progression and should be considered; d) This is a preliminary study and large-scale patient studies are needed for further improvements and validations
5. Conclusion
This study performs prediction analysis on plaque progression using morphological and biomechanical factors at baseline scan. PWS was the optimal predictor for PAI and WTI among all single risk factors. Results from predictive models proved our hypothesis that morphological and biomechanical factors integrated together could provide higher prediction accuracy than any single risk factor alone.
Supplementary Material
Figure S1. Selected IVUS-VH and contour plots from matched slices set at baseline and follow-up for all 9 patients. For each patient, Row 1: Baseline IVUS-VH; Row 2: Baseline contours; Row 3: Follow-up IVUS-VH; Row 4: Rotated follow-up contours.
Table S1: Patient-wise values of 8 morphological and biomechanical risk factors. Except plaque volume and lipid percent, the average values of the risk factors over all the slices within one patient were taken as patient-wise values. Lipid percent was calculated as the ratio of lipid volume and plaque volume. Plaque Volume Increase (PVI) used to measure plaque progression is defined as: Plaque Volume Increase = Plaque Volume at Follow-up - Plaque Volume at Baseline for each patient).
Acknowledgments
This research was supported by US NIH/NIBIB R01 EB004759. Tang's research was supported in part by National Sciences Foundation of China grants 11672001 and a Jiangsu Province Science and Technology Agency grant BE2016785.
Footnotes
Conflict of interest: The Authors disclose that they have no conflicts of interest.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bathe KJ. Theory and Modeling Guide. Vol I: ADINA; Vol II: ADINA-F, ADINA R & D, Inc; Watertown, MA: 2002. [Google Scholar]
- Bathe KJ. Finite element procedures. Prentice Hall, Englewood Cliffs; New Jersey: 1996. [Google Scholar]
- Bluestein D, Alemu Y, Avrahami I, Gharib M, Dumont K, Ricotta JJ, Einav S. Influence of microcalcifications on vulnerable plaque mechanics using FSI modeling. Journal of Biomechanics. 2008;41(5):1111–1118. doi: 10.1016/j.jbiomech.2007.11.029. [DOI] [PubMed] [Google Scholar]
- Caro CG, Fitz-Gerald JM, Schroter RC. Atheroma and arterial wall shear: Obervation, correlation and proposal of a shear dependent mass transfer mechanism of atherogenesis. Proc R Soc Lond B Biol Sci. 1971;177(1046):109–159. doi: 10.1098/rspb.1971.0019. [DOI] [PubMed] [Google Scholar]
- Corban MT, Eshtehardi P, Suo J, McDaniel MC, Timmins LH, Rassoul-Arzrumly E, Maynard C, Mekonnen G, King S, 3rd, Quyyumi AA, Giddens DP, Samady H. Cobination of plaque burden, wall shear stress, and plaque phenotype has incremental value for prediction of coronary atherosclerotic plaque progression and vulnerability. Atherosclerosis. 2014;232:271–276. doi: 10.1016/j.atherosclerosis.2013.11.049. [DOI] [PubMed] [Google Scholar]
- Friedman MH, Bargeron CB, Deters OJ, Hutchins GM, Mark FF. Correlation between wall shear and intimal thickness at a coronary artery branch, Atherosclerosis. 1987;68:27–33. doi: 10.1016/0021-9150(87)90090-6. [DOI] [PubMed] [Google Scholar]
- Fung YC, Liu SQ. Strain Distribution in Small Blood Vessel with Zero-Stress State Taken into Consideration. Am J Physiol. 1992;262(2):H544–52. doi: 10.1152/ajpheart.1992.262.2.H544. [DOI] [PubMed] [Google Scholar]
- Fry DL. Acute vascular endothelial changes associated with increased blood velocity gradients. Circ Res. 1968;22(2):165–197. doi: 10.1161/01.res.22.2.165. [DOI] [PubMed] [Google Scholar]
- Giddens DP, Zarins CK, Glagov S. The role of fluid mechanics in the localization and detection of atherosclerosis. J Biomech Engng. 1993;115:588–594. doi: 10.1115/1.2895545. [DOI] [PubMed] [Google Scholar]
- Gijsen FJH, Nieuwstadt HA, Wentzel JJ, Verhagen HJM, van der Lugt A, van der Steen AFW. Carotid plaque morphological classification compared with biomechanical cap stress: implications for a magnetic resonance imaging-based assessment. Stroke. 2015;46:2124–2128. doi: 10.1161/STROKEAHA.115.009707. [DOI] [PubMed] [Google Scholar]
- Glagov S, Wisenberg E, Zarins CK, Stankunavicius R, Kolettis GJ. Compensatory enlargement of human atherosclerotic coronary arteries. N Engl J Med. 1987;316:1371–1375. doi: 10.1056/NEJM198705283162204. [DOI] [PubMed] [Google Scholar]
- Guo X, Zhu J, Maehara A, Monoly D, Samady H, Wang L, Billiar KL, Zheng J, Yang C, Mintz GS, Giddens DP, Tang D. Quantify patient-specific coronary vessel material property and its impact on plaque stress/strain calculations using in vivo IVUS data and 3D FSI models: a pilot study. Biomechanics and Modeling in Mechanobiology. 2017;16(1):333–344. doi: 10.1007/s10237-016-0820-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holzapfel GA, Gasser TC, Ogden RW. A new constitutive framework for arterial wall mechanics and a comparative study of material models. Journal of elasticity and the physical science of solids. 2000;61(1):1–48. [Google Scholar]
- Kafi O, Khatib NE, Tiago J, Sequeira A. Numerical simulations of a 3D fluid-structure interaction model for blood flow in an atherosclerotic artery. Math Biosci Eng. 2017;14(1):179–193. doi: 10.3934/mbe.2017012. [DOI] [PubMed] [Google Scholar]
- Ku DN, Giddens DP, Zarins CK, Glagov S. Pulsatile flow and atherosclerosis in the human carotid bifurcation: positive correlation between plaque location and low and oscillating shear stress. Arteriosclerosis. 1985;5:293–302. doi: 10.1161/01.atv.5.3.293. [DOI] [PubMed] [Google Scholar]
- Kural MH, Cai M, Tang D, Gwyther T, Zheng J, Billiar KL. Planar biaxial characterization of diseased human coronary and carotid arteries for computational modeling. J Biomech. 2012;45(5):790–798. doi: 10.1016/j.jbiomech.2011.11.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loree HM, Kamm RD, Stringfellow RG, Lee RT. Effects of fibrous cap thickness on peak circumferential stress in model atherpsclerotic vessels. Circ Res. 1992;71:850–858. doi: 10.1161/01.res.71.4.850. [DOI] [PubMed] [Google Scholar]
- Malek AM, Alper SL, Izumo S. Hemodynamic shear stress and its role in atherosclerosis. JAMA. 1999;282(21):2035–2042. doi: 10.1001/jama.282.21.2035. [DOI] [PubMed] [Google Scholar]
- Maurice RL, Ohayon J, Finet G, Cloutier G. Adapting the Lagrangian speckle model estimator for endovascular elastography: Theory and validation with simulated radio-frequency data. J Acoust Soc Am. 2004;116(2):1276–1286. doi: 10.1121/1.1771615. [DOI] [PubMed] [Google Scholar]
- Ohayon J, Dubreuil O, Tracqui P, Le Floc'h S, Rioufol G, Chalabreysse L, Thivolet F, Pettigrew RI, Finet G. Influence of residual stress/strain on the biomechanical stability of vulnerable coronary plaques: potential impact for evaluating the risk of plaque rupture. Am J Physiol Heart Circ Physiol. 2007;293(3):H1987–96. doi: 10.1152/ajpheart.00018.2007. [DOI] [PubMed] [Google Scholar]
- Ohayon J, Finet G, Gharib AM, Herzka DA, Tracqui P. Necrotic core thickness and positive arterial remodeling index: Emergent biomechanical factors for evaluating the risk of plaque rupture. Am J Physiol Heart Circ Physiol. 2008;295:H717–H727. doi: 10.1152/ajpheart.00005.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohayon J, Gharib AM, Garcia A, Heroux J, Yazdani SK, Malve M, Tracqui P, Martinez M, Doblare M, Finet G, Pettigrew RI. Is arterial wall-strain stiffening and additional process responsible for atherosclerosis in coronary bifurcations? in vivo Study Based on Dynamic CT and MRI. Am J Physiol Heart Circ Physiol. 2011;301:H1097–106. doi: 10.1152/ajpheart.01120.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakellarios AI, Raber L, Boureantas CV, Exarchos TP, Athanasiou LS, Pelosi G, Koskinas KC, Parodi O, Naka KK, Michalis LK, Serruys PW, Garcia-Garcia HM, Windecker S, Fotiadis DI. Prediction of atherosclerotic plaque development in an in vivo coronary arterial segment based on a multilevel modeling approach. IEEE Transactions on Biomedical Engineering. 2017;64(8):1721–1730. doi: 10.1109/TBME.2016.2619489. [DOI] [PubMed] [Google Scholar]
- Samady H, Eshtehardi P, McDaniel MC, Suo J, Dhawan SS, Maynard C, Timmins LH, Quyyumi AA, Giddens DP. Coronary artery wall shear stress is associated with progression and transformation of atherosclerotic plaque and arterial remodeling in patients with coronary artery disease. Circulation. 2011;124:779–788. doi: 10.1161/CIRCULATIONAHA.111.021824. [DOI] [PubMed] [Google Scholar]
- Stary HC, Chandler AB, Dinsmore RE, Fuster V, Glagov S, Insull W, Jr, Rosenfeld ME, Schwartz CJ, Wagner WD, Wissler RW. A Definition of Advanced Types of Atherosclerotic Lesions and a Histological Classification of Atherosclerosis: A Report from the Committee on Vascular Lesions of the Council on Arteriosclerosis, American Heart Association. Circulation. 1995;92(5):1355–1374. doi: 10.1161/01.cir.92.5.1355. [DOI] [PubMed] [Google Scholar]
- Stone GW, Maehara A, Lansky AJ, de Bruyne B, Cristea E, Mintz GS, Mehran R, McPherson J, Farhat N, Marso SP, Parise H, Templin B, White R, Zhang Z, Serruys PW the PROSPECT Investigators. A prospective natural-history study of coronary atherosclerosis. N Engl J Med. 2011;364(3):226–35. doi: 10.1056/NEJMoa1002358. [DOI] [PubMed] [Google Scholar]
- Stone PH, Saito S, Takahashi S, Makita Y, Nakamura S, Kawasaki T, Takahashi A, Katsuki T, Nakamura S, Namiki A, Hirohata A, Matsumura T, Yamazaki S, Yokoi H, Tanaka S, Otsuji S, Yoshimachi F, Honye J, Harwood D, Reitman M, Coskun AU, Papafaklis MI, Feldman CL. Prediction of progression of coronary artery disease and clinical outcomes using vascular profiling of endothelial shear stress and arterial plaque characteristics: the PREDICTION Study. Circulation. 2012;126(2):172–81. doi: 10.1161/CIRCULATIONAHA.112.096438. [DOI] [PubMed] [Google Scholar]
- Tang D, Kamm RD, Yang C, Zheng J, Canton G, Bach R, Huang X, Hatsukami TS, Zhu J, Ma G, Maehara A, Mintz GS, Yuan C. Image-based modeling for better understanding and assessment of atherosclerotic plaque progression and vulnerability: data, modeling, validation, uncertainty and predictions. J Biomech. 2014;47(4):834–46. doi: 10.1016/j.jbiomech.2014.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang D, Teng Z, Canton G, Yang C, Ferguson M, Huang X, Zheng J, Woodard PK, Yuan C. Sites of rupture in human atherosclerotic carotid plaques are associated with high structural stresses: an in vivo MRI-based 3D fluid-structure interaction study. Stroke. 2009;40(10):3258–3263. doi: 10.1161/STROKEAHA.109.558676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teng Z, Zhang Y, Huang Y, Feng J, Yuan J, Lu Q, Sutcliffe MP, Brown AJ, Jing Z, Gillard JH. Material properties of components in human carotid atherosclerotic plaques: A uniaxial extension study. Acta Biomater. 2014;(14):S1742–7061. 00379–1. doi: 10.1016/j.actbio.2014.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venables WN, Ripley BD. Modern Applied Statistics with S. 4th. Springer; New York: 2002. [Google Scholar]
- Virmani R, Kolodgie FD, Burke AP, Farb A, Schwartz SM. Lessons from sudden coronary death: a comprehensive morphological classification scheme for atherosclerotic lesions. Arterioscler Thromb Vasc Biol. 2000;20(5):1262–1275. doi: 10.1161/01.atv.20.5.1262. [DOI] [PubMed] [Google Scholar]
- Wang L, Zheng J, Maehara A, Yang C, Billiar KL, Bach R, Muccigrosso D, Mintz GS, Tang D. Morphological and Stress Vulnerability Indices for Human Coronary Plaques and Their Correlations with Cap Thickness and Lipid Percent: An IVUS-Based Fluid-Structure Interaction Multi-Patient Study, PLOS Computational Biology. 2015a;11(12):e1004652. doi: 10.1371/journal.pcbi.1004652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Wu Z, Yang C, Zheng J, Bach R, Muccigrosso D, Billiar KL, Maehara A, Mintz GS, Tang D. IVUS-Based FSI Models for Human Coronary Plaque Progression Study: Components, Correlation and Predictive Analysis. Annals of Biomedical Engineering. 2015b;43(1):107–121. doi: 10.1007/s10439-014-1118-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Z, Yang C, Tang D. In vivo serial MRI-based models and statistical methods to quantify sensitivity and specificity of mechanical predictors for carotid plaque rupture: location and beyond. J Biomech Eng. 2011;133(6):064503. doi: 10.1115/1.4004189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang C, Bach R, Zheng J, El Naqa I, Woodard PK, Teng ZZ, Billiar KL, Tang D. In vivo IVUS-based 3D fluid structure interaction models with cyclic bending and anisotropic vessel properties for human atherosclerotic coronary plaque mechanical analysis, IEEE Trans. Biomed Engineering. 2009;56(10):2420–2428. doi: 10.1109/TBME.2009.2025658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang C, Tang D, Yuan C, Hatsukami TS, Zheng J, Woodard PK. In Vivo/Ex Vivo MRI-Based 3D Non-Newtonian Models with Fluid-Structure Interactions for Human Atherosclerotic Plaques Compared with Fluid/Wall-Only Models, CMES: Computer Modeling in Engineering and Sciences. 2007;19(3):233–245. 2007. [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1. Selected IVUS-VH and contour plots from matched slices set at baseline and follow-up for all 9 patients. For each patient, Row 1: Baseline IVUS-VH; Row 2: Baseline contours; Row 3: Follow-up IVUS-VH; Row 4: Rotated follow-up contours.
Table S1: Patient-wise values of 8 morphological and biomechanical risk factors. Except plaque volume and lipid percent, the average values of the risk factors over all the slices within one patient were taken as patient-wise values. Lipid percent was calculated as the ratio of lipid volume and plaque volume. Plaque Volume Increase (PVI) used to measure plaque progression is defined as: Plaque Volume Increase = Plaque Volume at Follow-up - Plaque Volume at Baseline for each patient).