Model‐Based Evaluation of Radiation and Radiosensitizing Agents in Oncology

Abstract

Radiotherapy is one of the major therapy forms in oncology, and combination therapies involving radiation and chemical compounds can yield highly effective tumor eradication. In this paper, we develop a tumor growth inhibition model for combination therapy with radiation and radiosensitizing agents. Moreover, we extend previous analyses of drug combinations by introducing the tumor static exposure (TSE) curve. The TSE curve for radiation and radiosensitizer visualizes exposure combinations sufficient for tumor regression. The model and TSE analysis are then tested on xenograft data. The calibrated model indicates that the highest dose of combination therapy increases the time until tumor regrowth 10‐fold. The TSE curve shows that with an average radiosensitizer concentration of $1.0\hspace{0.17em}\mathrm{\mu }\mathbf{g}/\mathbf{m}\mathbf{L}$ the radiation dose can be decreased from $2.2 \mathbf{G}\mathbf{y}$ to $0.7 \mathbf{G}\mathbf{y}$. Finally, we successfully predict the effect of a clinically relevant treatment schedule, which contributes to validating both the model and the TSE concept.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE OF THE TOPIC?

☑ Tumor growth inhibition (TGI) models are commonly used to describe chemical interventions. Tumor static concentration (TSC) curves have been introduced for combinations of chemical agents.

WHAT QUESTION DID THIS STUDY ADDRESS?

☑ Can we extend current TGI models to describe radiotherapy and combination therapies involving radiation? Can the TSC concept be extended to such models?

WHAT THIS STUDY ADDS TO OUR KNOWLEDGE

☑ The proposed model combines existing TGI models with the linear‐quadratic theory of radiobiology. The model contains relatively few parameters and can be calibrated to data from standard xenograft studies. The tumor static exposure (TSE) curve is introduced by considering average, as opposed to pointwise, tumor stasis.

HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

☑ The proposed tumor model can be used to simulate and predict therapies involving radiation to guide future experiments. The model also has the potential to be used as a translational tool to guide clinical studies. The TSE curve can be used to evaluate, rank, and compare radiosensitizing agents.

Combination therapies have become increasingly clinically relevant and have multiple potential advantages over single‐agent treatment.1 By targeting the disease along multiple pathways, the increasing problem of drug resistance can be reduced.2 There is also a potential for drug synergies.3, 4 Synergistic interactions can take many forms. For instance, a pharmacokinetic synergy could mean that a drug decreases the clearance of another, leading to an increased exposure of the latter. Similarly, a pharmacodynamic synergy could be that one drug increases the sensitivity to another.5

We have previously developed model‐based methods to quantitatively assess combination therapies of chemotherapeutic drugs using the so‐called tumor static concentration (TSC) curve.6, 7, 8 The TSC curve is defined by all concentration pairs that result in tumor stasis according to a suitable tumor model. The TSC curve determines sufficient drug exposures for tumor regression, and highlights potential inherent benefits of combining the two agents. It can also be used to optimize dosing regimens for maintained tumor regression, and can aid in evaluating the performance of different drug combinations. Furthermore, the curvature of the TSC curve is related to drug interactions, with synergy and antagonism resulting in a more convex or concave (curving below or above a straight line connecting two points on the curve) TSC curve, respectively. The TSC curve is visually similar to the well‐established isobologram, but the TSC curve involves plasma concentrations (i.e., exposure), as opposed to doses.9, 10 Recently, another TSC‐like curve called the “half‐maximal effect curve” was introduced based on general combination effect expressions.11 The TSC curve is currently only applicable to chemical compounds with known plasma exposures. Therefore, it would be desirable to extend the TSC concept to other important therapies, such as radiation.

Radiotherapy is one of the major approaches in oncology along with chemotherapy and surgery.12 Ionizing radiation (IR) damages the DNA of the cancer cells, causing them to die through a variety of mechanisms, including apoptosis, autophagy, necrosis, senescence, and mitotic catastrophe.13, 14 Specifically, IR induces DNA single‐strand and double‐strand breaks that, if unrepaired, are likely to result in cell death. Mathematical models of radiotherapy have been proposed with various levels of detail, ranging from the linear‐quadratic (LQ) model of the surviving fraction of cells, to systems of partial differential equations describing both temporal and spatial tumor growth.15, 16, 17, 18, 19 In the clinic, the LQ model is widely used and has a strong empirical basis.20, 21 A definitive derivation of the model does not exist, although many potential derivations have been proposed.22, 23

Radiotherapy can be given before, after, or alongside chemotherapy, giving rise to potential interactions. A chemical compound acting synergistically with IR could mean a net increase in the DNA damage caused by irradiation, or that the compound facilitates one or several of the possible mechanisms of cell death of the DNA‐damaged cells.24 For chemotherapeutic drugs, so‐called tumor growth inhibition (TGI), models involving a set of damage compartments have become a well‐established way of modeling volume‐time data.25, 26, 27

In this paper, we introduce a TGI model for treatments involving both ionizing radiation and chemical compounds. In particular, we focus on the case in which the compound is a radiosensitizer that enhances the effect of the radiotherapy. The proposed model can be viewed an extension of traditional TGI models to radiotherapy, but it also has a basis in the LQ theory of radiobiology. Based on this model, we extend the TSC concept to combinations involving ionizing radiation by introducing the tumor static exposure (TSE) curve. The analysis is based on requiring the growth of the tumor to be zero not at each point in time, but on average over a certain time period. Our tumor model and TSE analysis are illustrated using xenograft data. The model is able to adequately describe both monotherapy and combination therapy at different dose levels. The TSE curve visualizes how the radiation effect is enhanced by the radiosensitizer, significantly lowering the radiation exposure necessary for tumor regression. We also consider the implications of between‐subject variability on the TSE curve. Finally, we use the calibrated tumor model to predict the treatment effect of a clinically relevant administration schedule. This prediction can be viewed as a validation example of both the tumor model and of the associated TSE curve.

METHODS

In this section, we introduce a general TGI model for combination therapy with ionizing radiation and radiosensitizing compounds. Thereafter, we extend the TSC concept to such models by defining what we call the TSE curve.

Radiation and chemical tumor growth inhibition model

Untreated tumor growth is described using a model with one main compartment and three damage compartments, as described in ref. 7. The main compartment $V_1$ represents the volume of proliferating cancer cells and follows logistic growth with exponential growth rate $k_g$ and tumor capacity parameter $K$. Natural cell death is modeled using the three damage compartments $V_2$, $V_3$, and $V_4$ with kill rate parameter $k_k$.

The action of ionizing radiation is incorporated as an instant mass transfer between compartments $V_1$ and $U_1$ at the time of irradiation. The compartments $U_1$ and $U_2$ can be interpreted in the following way: Cancer cells that are lethally irradiated are transferred to $U_1$ where they are allowed up to one more cell division. The daughter cells are transferred to $U_2$ where they can no longer proliferate and will eventually die. The inclusion of $U_1$ and $U_2$ ensures that the total tumor volume is continuously differentiable.

According to the LQ theory, the average number of lethal lesions $L$ inflicted by a radiation dose $D$ is given by the sum of a linear and a quadratic term with coefficients α and β, respectively.19

$$L=\hspace{0.17em}\alpha D+\beta D^2$$ (1)

The standard assumption is that such lesions are Poisson distributed from cell to cell.19 Hence, the probability of having $k=0$ lethal lesions occurring in a cell is given by:

$$P\left(k=0\right)=\hspace{0.17em}\frac{L^0\exp \left(-L\right)}{0!}=\exp \left(-L\right)$$ (2)

and by independence, the surviving fraction of cells, $SF\left(D\right)$, as a function of radiation dose is given by:

$$SF\left(\mathrm{D}\right)=\exp \left(-L\right)=\mathrm{e}\mathrm{x}\mathrm{p}(-\alpha D-\beta D^2)$$ (3)

Hence, the radiation‐induced mass transfer was chosen as:

$$1-SF\left(D\right)=1-\mathrm{e}\mathrm{x}\mathrm{p}(-\alpha D-\beta D^2)$$ (4)

Radiosensitizers can have many different mechanisms of action. To make the model generally applicable, we lump all of these processes together as having the net action of stimulating the radiation‐induced mass transfer. We use a linear stimulatory function $S\left(C\right)=1+bC$ to describe this action, where $b$ is a pharmacodynamic parameter associated with the radiosensitizing effect. Taking such an effect into account, the modified surviving fraction for combination therapy with radiation dose $D$ and concurrent plasma concentration of the radiosensitizer $C$ will therefore be:

$$SF\left(D,C\right)=\exp \left[-(1+bC)\left(\alpha D+\beta D^2\right)\right]$$ (5)

Should the radiosensitizer also exhibit a monotherapy effect, this can be described in a standard way (e.g., as a linear stimulation of the natural death process of proliferating cancer cells with pharmacodynamic parameter $a$).

The full tumor model is depicted in Figure 1. The corresponding system of differential equations reads:

$$\begin{array}{l}\frac{d{V}_1}{dt}=\hspace{0.17em}{k}_g{V}_1\left(1-\frac{V_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}{K}\right)-(1+aC)k_k{V}_1-\left(1-SF\left(D,C\right)\right)R V_{1 }\\ \frac{d{V}_2}{dt}=(1+aC)k_k{V}_1+k_k{U}_1+k_k{U}_2-k_k{V}_2\\ \frac{d{V}_3}{dt}=\hspace{0.17em}{k}_k{V}_2-k_k{V}_3\\ \frac{d{V}_4}{dt}=\hspace{0.17em}{k}_k{V}_3-k_k{V}_4\\ \frac{d{U}_1}{dt}=\left(1-SF\left(D,C\right)\right) R V_1-k_g{U}_1\left(1-\frac{V_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}{K}\right)-k_k{U}_1\\ \frac{d{U}_2}{dt}=\hspace{0.17em}2k_g{U}_1\left(1-\frac{V_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}{K}\right)-\hspace{0.17em}{k}_k{U}_2\end{array}$$ (6)

Figure 1.

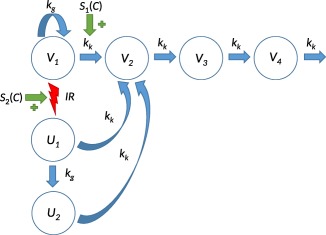
Tumor model describing combination therapy with ionizing radiation and a generic radiosensitizer. Viable cancer cells in compartment $V_1$ proliferate with rate $k_g$ and die naturally with rate $k_k$. Dying cells traverse a set of three damage compartments ( $V_2$, $V_3$, and $V_4$) before exiting the system. Upon irradiation (IR), a fraction of viable cells are moved from $V_1$ to $U_1$, after which the irradiated cells can divide one more time at most, and in the process transferring the daughter cells to $U_2$, where the cells can no longer proliferate and will eventually die. Plasma concentration of the radiosensitizer $C\left(\mathrm{t}\right)$ can stimulate either or both the natural‐induced and the radiation‐induced transfer of viable cancer cells.

where $k_g$ is the growth rate, $k_k$ the kill rate, $K$ the tumor capacity, $R$ the radiation rate function for radiation consisting of a series of Dirac delta distributions, $\alpha$ and $\beta$ the radiation parameters, and $a$ and $b$ pharmacodynamic parameters associated with the stimulation of the natural cell death and the radiation effect, respectively. Note the factor 2 in the equation for $U_2$ representing the fact that irradiated cells are still able to proliferate once. The initial conditions should be chosen as:

$$V_i\left(0\right)=V^0{\left(\frac{k_k}{k_g}\right)}^{i-1}{,\hspace{0.17em}U}_i\left(0\right)=0,$$ (7)

where $V^0$ is the initial volume of the main compartment. These initial conditions ensure that untreated tumors grow exponentially with rate $k_g-k_k$, see the derivation in ref. 7. The total tumor volume $V_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}$ comprises all six compartments:

$$V_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}=V_1+V_2+V_3+V_4+U_1+U_2$$ (8)

Tumor static exposure

In previous studies, TSC values and TSC curves were derived based on a condition of input and output balances for each compartment (i.e., constant tumor stasis).6, 7, 28 For the model in Eq. 6, it suffices to only consider the main compartment, because if the main compartment is kept in stasis, the other compartments will eventually reach stasis as well. Moreover, the decrease in tumor growth rate for large tumors introduced by the tumor capacity should be ignored, because the treatment goal is tumor shrinkage. Using Eq. 6, the TSC condition would therefore be:

$$k_g-(1+aC)k_k-\left[1-\exp \left(-(1+bC)\left(\alpha D+\beta D^2\right)\right)\right]\hspace{0.17em}R\hspace{0.17em}=0$$ (9)

However, Eq. 9 cannot be solved directly, because the radiation rate function $R$ contains Dirac delta distributions and is, therefore, not point‐wise defined. This issue can be circumvented by, instead of requiring tumor stasis at each time point, one only requires tumor stasis in an average sense over a treatment period between times $t=0$ and $t=T.$ 29

We say that the main compartment is in stasis in an average sense between $t=0$ and $t=T$ if $V_1\left(T\right)=V_1\left(0\right)$. A TSE expression can then be derived in the following way. Upon irradiation, only a fraction of proliferating cells survive. These fractions will then regrow and at some point reach their original volume. The TSE condition is imposed by requiring the main compartment to reach its original volume at time $T$ when the next dose of radiation occurs. The derivation of the expressions that follow can be found in Supplementary Material SA.

For treatment only with radiation the TSE value becomes:

$$D=\frac{-\alpha +\sqrt{{\alpha }^2+4\beta \left(k_{g}T-k_{k}T \right)}}{2\beta }$$ (10)

Eq. 10 can also be interpreted in the following way. Any dose greater than the one given in Eq. 10, will result in the main compartment shrinking. Upon repeated dosing every $T$ days, the entire tumor will eventually shrink and subsequently be eradicated. Furthermore, doses below the one specified in Eq. 10 will be insufficient for tumor regression and will only slow down the tumor growth.

Similarly, for monotherapy with the radiosensitizer the TSE value is:

$$\overline{C}=\hspace{0.17em}\frac{k_g-k_k}{a{ k}_k}$$ (11)

Eq. 11 has the following analogous interpretation. Assuming bolus dosing every $T$ days with the radiosensitizer alone, the tumor will shrink if the average plasma concentration is above the one specified in Eq. 11. Moreover, an average plasma concentration below this value will only slow down the tumor growth but cannot reverse it.

Finally, for combination therapy with radiation and radiosensitizer the TSE expression becomes:

$$D=\frac{-G\left(\alpha \right)+\sqrt{{G\left(\alpha \right)}^2+4G\left(\beta \right)\left(k_{g}T-k_{k}T-k_{k}a \overline{C} \right)}}{2G\left(\beta \right)}$$ (12)

where the function $G$ depends on the pharmacokinetics of the radiosensitizer. In particular, for a standard one‐compartment model:

$$\mathrm{G}\left(\mathrm{x}\right)=x+bx\frac{\overline{C}{k}_{e}T}{1-e^{-k_{e}T}}$$ (13)

Eq. 12 describes the concentration‐dose pairs that give average tumor stasis. For any average concentration $\overline{C}$ of the radiosensitizer, Eq. 12 gives the necessary radiation dose such that combination treatment will keep the tumor in stasis. In particular, by inserting $\overline{C}=0$, Eq. 12 reduces to Eq. 10, and similarly, letting $D=0$ and solving for $\overline{C}$ results in Eq. 11. Geometrically, Eq. 12 describes a curve in the concentration‐dose plane and is called the TSE curve, because plasma concentration and radiation dose are two different types of exposure.

Experimental data

The tumor model and TSE analysis were tested on data generated in FaDu xenograft models treated with radiation and/or a small molecule discovery compound that inhibits the repair of radiation‐induced DNA damage, henceforth referred to as RS1. Eighty mice were divided into eight treatment groups with 10 mice in each of the following groups: (A) vehicle; (B) radiation ( $2 \mathrm{G}\mathrm{y}$); (C–E) RS1 ( $10,\hspace{0.17em}50,\hspace{0.17em}\mathrm{o}\mathrm{r} 200 \mathrm{m}\mathrm{g}/\mathrm{k}\mathrm{g}$); and (F–H) combination therapy with radiation ( $2 \mathrm{G}\mathrm{y}$) and RS1 ( $10,\hspace{0.17em}50,\hspace{0.17em}\mathrm{o}\mathrm{r} 200 \mathrm{m}\mathrm{g}/\mathrm{k}\mathrm{g}$). Dosing occurred every day for 5 days. A second dataset consisting of 10 mice receiving combination therapy with radiation ( $2 \mathrm{G}\mathrm{y}$) and RS1 ( $25 \mathrm{m}\mathrm{g}/\mathrm{k}\mathrm{g}$) 5 days a week for 6 weeks, was used for model validation. All experiments were approved in accordance with the German animal welfare regulations by the Regierungspräsidium Darmstadt, Hessen, Germany (protocol registration numbers DA 4/Anz. 397 and DA 4/Anz. 398). Further details on the experiments can be found in Supplementary Material SB.

Computational methods

Nonlinear mixed‐effects modeling was performed using a first‐order conditional estimation method in a computational framework developed at the Fraunhofer‐Chalmers Research Centre for Industrial Mathematics (Gothenburg, Sweden) and implemented in Mathematica (Wolfram Research).30 Exposure data were first fitted to a pharmacokinetic model. Afterward, the pharmacodynamic data were fitted simultaneously to the tumor model. The tumor model was driven by the complete population pharmacokinetic model (i.e., not just the median individual). Model evaluation was based on goodness‐of‐fit, Empirical Bayes Estimates, and residual analysis.

Log‐normal between‐subject variability was allowed in initial tumor volume, capacity, distribution volume, and elimination rate. Residual errors were assumed to be proportional to tumor volume with zero mean and variance ${\sigma }_V^2$. Because data only included one radiation dose, the ratio between $\alpha$ and $\beta$ was fixed to 10, which is a plausible value for tumors.31

RESULTS

The tumor model and TSE analysis were applied to in vivo data. The purpose was twofold. First, to illustrate how these concepts can be applied in practice, and second, to validate the usefulness of the developed methods.

Radiation and chemical tumor growth inhibition model

Exposure to RS1 was adequately described using a one‐compartment model. The parameter estimates are given in Supplementary Table S1. Drug elimination was rapid, with an estimated half‐life of 3 hours. Simulated exposure profiles are shown in Supplementary Figure S1. Visual predictive checks can be found in Supplementary Material SC.

The tumor model successfully captured all eight treatment groups. Examples of individual fit for one individual in each of the treatment groups A, B, and E–H are shown in Figure 2. Vehicle A exhibited approximately exponential growth. Monotherapy with RS1 showed only a small deviation from the vehicle group, even with the highest dose of $200 \mathrm{m}\mathrm{g}/\mathrm{k}\mathrm{g}$ in vehicle E. In contrast, monotherapy with radiation (vehicle B) resulted in slowing down the tumor growth considerably, but was insufficient for regression. When radiation and RS1 were given simultaneously (vehicles F–H), there was a substantial increase in the dose‐related treatment effect. Combination therapy with the highest dose ( $200 \mathrm{m}\mathrm{g}/\mathrm{k}\mathrm{g}$), showed rapid tumor regression and, in most cases, the tumors were completely eradicated after 30 days. Visual predictive checks can be found in Supplementary Material SC.

Figure 2.

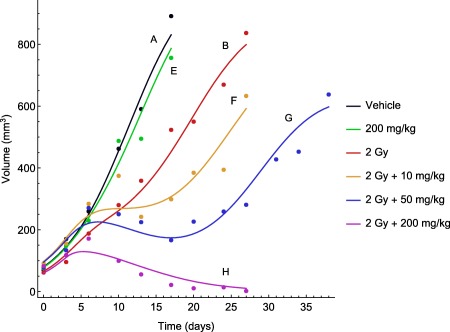
Representative time courses of observed tumor volumes (circles) and model‐fitted tumor growth (solid lines) for the following treatment groups: (A) vehicle; (B) radiotherapy (2 Gy per dose); (E) RS1 monotherapy (200 $\mathrm{m}\mathrm{g}/\mathrm{k}\mathrm{g}$ per dose); and (F–H) combination therapy with radiation (2 Gy per dose) and RS1 (10, 50, or 200 $\mathrm{m}\mathrm{g}/\mathrm{k}\mathrm{g}$ per dose).

The parameter estimates from fitting the tumor model simultaneously to all eight treatment group are given in Table 1. The net growth rate $k_g-k_k\hspace{0.17em}=0.22 {day}^{-1}$ corresponds to a doubling time of 3.15 days that, however, slows down as the tumors approach the capacity level. The total initial volume, computed as the sum of all compartment volumes at time zero, was $87 {\mathrm{m}\mathrm{m}}^3$. All parameters were estimated with good or reasonable precision.

Table 1.

Parameter estimates for the tumor model describing the effects of radiation and RS1 combination therapy.

Parameter	Population median (RSE%)	Between‐subject variabilitya (RSE%)	Description
${ k}_g\hspace{0.17em}\left({\mathrm{d}\mathrm{a}\mathrm{y}}^{-1}\right)$	$0.50\hspace{0.17em}\left(3\right)$	$-$	Natural growth rate
${ k}_k\hspace{0.17em}\left({\mathrm{d}\mathrm{a}\mathrm{y}}^{-1}\right)$	$0.28\hspace{0.17em}\left(2\right)$	$-$	Natural kill rate
$K\hspace{0.17em}\left(\mathrm{m}{\mathrm{m}}^3\right)$	$2200\hspace{0.17em}\left(8\right)$	$32\hspace{0.17em}\left(7\right)$	Tumor capacity
${ V}^0\hspace{0.17em}\left(\mathrm{m}{\mathrm{m}}^3\right)$	$40.0\hspace{0.17em}\left(3\right)$	$21\hspace{0.17em}\left(6\right)$	Initial volume of main compartment
$\hspace{0.17em}\alpha \hspace{0.17em}\hspace{0.17em}\left({\mathrm{G}\mathrm{y}}^{-1}\right)$	$0.08 \left(13\right)$	$-$	Linear radiation parameter
$\hspace{0.17em}\beta \hspace{0.17em}\hspace{0.17em}\left({\mathrm{G}\mathrm{y}}^{-2}\right)$	$0.008\hspace{0.17em}\left(13\right)$	$-$	Quadratic radiation parameter
$\mathrm{a}\hspace{0.17em}\hspace{0.17em}(\mathrm{m}\mathrm{L}/\mathrm{\mu }\mathrm{g})$	$0.09\hspace{0.17em}\left(31\right)$	$-$	Stimulation of natural cell death
$\mathrm{b}\hspace{0.17em}\hspace{0.17em}(\mathrm{m}\mathrm{L}/\mathrm{\mu }\mathrm{g})$	$0.45\hspace{0.17em}\left(27\right)$	$-$	Stimulation of radiation‐induced cell death
${\sigma }_{\mathrm{V}}^{\mathrm{b}}$ (%)	$23.0\hspace{0.17em}\left(10\right)$	$-$	Proportional standard error

RSE, relative standard error.

^aCalculated as $\sqrt{{\omega }_{\mathrm{i}\mathrm{i}}^2}\times 100$.

^bIntra‐individual variability.

TSE curve of radiation and radiosensitizer

The TSE curve for combinations of radiation and RS1 was computed by inserting the population parameter estimates from Table 1 into Eq. 12 with $T=1$ for daily dosing. The TSE curve is shown in blue in Figure 3. Concentration‐dose pairs above the curve (green area) signify tumor shrinkage, whereas those below (red area) signify tumor growth. The black dashed line represents a zero interaction reference (i.e., what the curve would have looked like for $b=0$; see Eq. 12). The TSE curve has a significant downward curvature, indicating a strong synergistic effect between IR and RS1. From the curve's intersections with the coordinate axes, or by using Eqs. 10 and 11, one can see that, if radiation is administered as monotherapy, the daily dose required to achieve tumor regression (i.e., the TSE value) is predicted to be $2.2 \mathrm{G}\mathrm{y}$, whereas if only RS1 is administered, the required average exposure is 8.3 $\mathrm{\mu }\mathrm{g}/\mathrm{m}\mathrm{L}$. Furthermore, by following the TSE curve as exposure to RS1 is increased, we see that when the concentration reaches $1.0\hspace{0.17em}\mathrm{\mu }\mathrm{g}/\mathrm{m}\mathrm{L}$, the radiation dose can be reduced from $2.2 \mathrm{G}\mathrm{y}$ with monotherapy to ∼ $0.7 \mathrm{G}\mathrm{y}$ per day with combination therapy. To confirm the accuracy of the TSE curve, the model was simulated for different exposure pairs on the TSE curve, see Supplementary Material SD.

Figure 3.

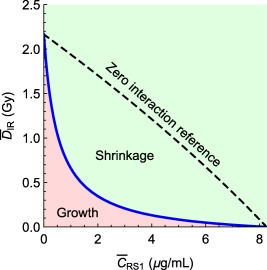
Tumor static exposure curve for radiation and radiosensitizer. Concentration‐dose pairs above the curve give tumor shrinkage, whereas those below give tumor growth. The synergistic effect gives rise to a large curvature compared to the zero interaction reference.

Based on between‐subject variability in the parameters $K$, $V_0$, and $k_e$, individual TSE curves were computed for each of the 80 individuals. These are shown in Figure 4. Although the individual TSE values remain approximately the same, there is noticeable variation in curvature, and, hence, variation in synergy between different individuals.

Figure 4.

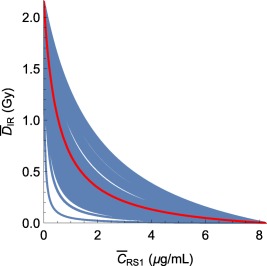
(Blue) Computed tumor static exposure (TSE) curves for all of the 80 individuals in the combination therapy experiment, assuming a maintained daily administration schedule, and (red) TSE curve for the median individual. The curvature of individual TSE curves varies considerably.

Prediction for 6‐week treatment

Using the parameter estimates from Table 1, the tumor model was used to simulate the treatment effect of 6 weeks of combination therapy with $25 \mathrm{m}\mathrm{g}/\mathrm{k}\mathrm{g}$ (corresponding to an average concentration of $0.52\hspace{0.17em}\mathrm{\mu }\mathrm{g}/\mathrm{m}\mathrm{L}$) and $2 \mathrm{G}\mathrm{y}$ per dose at the population level and compared to a second dataset of 10 mice (Figure 5). These doses put the combination therapy barely inside the green shrinkage area in Figure 3. Therefore, the TSE curve predicts that prolonged treatment should result in tumor regression and ultimately tumor eradication. This is in agreement with the observed tumor volumes in Figure 5, most of which are eradicated by the end of the treatment period.

Figure 5.

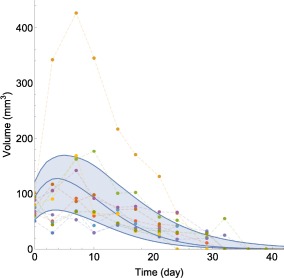
Comparison between model‐predicted and observed tumor volume evolutions for 6 weeks of combination therapy treatment with radiation ( $2 \mathrm{G}\mathrm{y}$ per dose) and RS1 ( $25 \mathrm{m}\mathrm{g}/\mathrm{k}\mathrm{g}$ per dose). Blue curves represent simulated 5th, 50th, and 95th percentiles based on the tumor model (Eqs. 6 and 7) and parameter estimates from Table 1 and Supplementary Table S1. Measured tumor volumes are indicated by dots with each color corresponding to a different animal.

Approximately 80% of the observations were inside the region between the simulated 5th and 95th percentiles. Moreover, observed tumor volumes appeared to be a bit smaller than predicted during the first 10 days of treatment, including at the initial measurements when treatment was started.

DISCUSSION

Combination therapies in oncology do not only include combinations of chemical compounds, but also commonly include ionizing radiation. When mathematical models and methods to describe and quantify anticancer combinations are developed, it is, therefore, desirable that they can, with minimal modification, be applied to treatments with chemical compounds, radiation, and combinations thereof. The tumor model we propose is based on traditional tumor growth inhibition models, but is modified using the LQ theory to describe radiotherapy. Similarly, the previously introduced TSC curve as a tool for evaluating anticancer combinations was only applicable to combinations of chemical agents and was, therefore, modified to handle radiation.

Radiation and chemical tumor growth inhibition model

The tumor model contains several simplifications. Radiation is modeled as an instantaneous mass transfer where damaged cells inevitably die. This is a simplification of a much more complicated process of many different mechanisms of cell death that can occur after irradiation. DNA damage may be repaired within a few hours, making it possible for some cells to return to a proliferating state again.32 Including these aspects into the model may be possible with additional sources of data. Assuming only total tumor volume is measured, it is necessary to lump all of these processes together into one step.

The same set of damage compartments is used for all kinds of cell death. This implies that the death processes are equivalent from a modeling perspective, which is consistent with the simplification above. As an alternative, some tumor models have been developed that use separate sets of damage compartments for each compound, the argument being that the death processes are completely independent.33, 34

The proposed tumor model was successfully able to describe the data from a xenograft study. Monotherapy with RS1 had a weak overall effect, represented by the parameter $a$. The estimated value of $0.09 \mathrm{m}\mathrm{L}/\mathrm{\mu }\mathrm{g}$ corresponds to an increase of the natural cell death by $9\%$ for each $\mathrm{\mu }\mathrm{g}/\mathrm{m}\mathrm{L}$. This effect did not have a significant impact on overall tumor regression and was dominated by radiation and interaction effects. Still, $a$ was estimated with reasonable precision, indicating that the differences between vehicle and RS1 monotherapy were small but noticeable, which can also be seen in the visual predictive checks in Supplementary Material SC. Moreover, because the monotherapy effect of RS1 was small, it should not have a significant impact on other parameter estimates. The interaction parameter $b$ was estimated to $0.45 \mathrm{m}\mathrm{L}/\mathrm{\mu }\mathrm{g}$. This means that, for sufficiently low doses of radiation, the fraction of cells killed is increased by $45\%$ for each $\mathrm{\mu }\mathrm{g}/\mathrm{m}\mathrm{L}$. Without this interaction, the combination therapy would not have performed significantly better than radiation alone.

The radiation parameters $\alpha$ and $\beta$ were estimated to be $0.08 {\mathrm{G}\mathrm{y}}^{-1}$ and $0.008 {\mathrm{G}\mathrm{y}}^{-2}$, respectively, and are of a similar order, as previously reported values.32 Using these estimates, a dose of $2 \mathrm{G}\mathrm{y}$ corresponds to $17\%$ of proliferating cells dying at each instance of irradiation. For combination therapy, the fraction of dying cells increases to $24$, $46$, and $85$%, with doses of $10$, $50$, and $200 \mathrm{m}\mathrm{g}/\mathrm{k}\mathrm{g}$, respectively. If cell proliferation is ignored, this means that after five doses of irradiation, $38\%$ of the cell population will survive, whereas for combination therapy with the highest dose, only 0.007% will survive. With such a small fraction of cells surviving, tumor eradication is highly likely. Furthermore, even if the tumor regrows it would take ∼10 times longer for the tumor to reach its original volume compared to if it was exposed only to radiation.

Between‐subject variability was allowed only for initial volume, capacity, and the pharmacokinetic parameters. Some scenarios with additional variability were tried, but did not result in an improved overall fit, likely because of the already large variability in RS1 exposure.

TSE curve of radiation and radiosensitizer

The TSE curve was introduced by conditioning on an average, as opposed to point‐wise, tumor growth of zero. This departure from previous TSC curves was necessary because radiotherapy was characterized by a series of Dirac delta pulses representing instances of irradiation.

An alternative way to introduce a TSE curve would have been to use Eq. 9 and replace $C$ with $\overline{C}$ and $D$ with $\overline{D}$ (and letting the rate function $R=1$). However, this would not yield accurate predictions of stasis, because it does not discriminate between how the averages are achieved. In particular, two administration schedules can have the same average exposure, but result in different tumor dynamics. In contrast, the way the TSE curve is introduced in this paper takes the administration schedule into account and should, therefore, yield more accurate predictions.

The TSE curve for radiation and RS1 combinations determine the necessary exposure levels for tumor regression for repeated dosing. This makes it possible to target exposure levels in the green regression area of the plot (Figure 3). The curve exhibits a large curvature, due to a significant interaction effect. Without the interaction (i.e., $b=0$), the TSE curve would have been approximately a straight line. The curvature increases the green area and, therefore, makes it easier to achieve tumor regression.

In contrast to TSC curves derived previously,7 the TSE curve depends on the administration schedule. For example, if radiation and radiosensitizer were given at well‐separated time points, there would be no plasma concentration in the system around the time of irradiation and the synergistic effect would vanish. The curve would then look closer to the zero interaction reference (Figure 3).

Given that the TSE curve is constructed using the median parameter values, exposure near the TSE curve will result in only half of the population showing tumor regression, whereas the other half is still showing tumor growth. Therefore, it is critical to examine how TSE varies in the population via the individual TSE curves (Figure 4). This makes it possible to target tumor regression for a larger percentage of the population. The parameters that are chosen to have between‐subject variability will impact how the individual TSE curves differ.

Finally, it is worth keeping in mind that the TSE curve and the associated synergy are based on xenografts. As future work, it would be interesting to consider how the model could be translated to the clinical setting. In particular, it would be interesting to see how well the synergy indicated by the TSE curve reflects the synergy in humans.

Prediction for 6‐week treatment

The prediction of a 6‐week treatment schedule using a second dataset can be viewed as a validation example of the tumor model and of the associated TSE curve. Importantly, these data were generated using a clinically relevant administration schedule. This reinforces the claim that the TSE concept can be useful and has practical significance. Overall, the prediction matched the outcome in the second experiment reasonably well. Admittedly, tumor regression occurred somewhat faster than predicted. This was likely due to the smaller initial tumor volumes and shorter delay of treatment effect compared to the primary dataset.

CONCLUSIONS AND PERSPECTIVES

A tumor model was introduced to describe combination therapy with radiation and radiosensitizing agents. The model was able to describe an in vivo dataset with eight different treatment groups and multiple dose levels. The model also provided a reasonable prediction of a second dataset with a clinically relevant 6‐week treatment schedule. Moreover, the TSE curve is introduced based on a condition of approximate tumor stasis. The TSE curve illustrates how easily a given anticancer combination can achieve tumor regression. Potential future work includes challenging the tumor model with additional radiosensitizing agents, using the TSE curve to discriminate between and rank different combination therapies while taking toxicological considerations into account, and using the model as a translational tool to predict and describe the outcome of clinical trials.

Conflict of Interest

The authors declared no conflict of interest.

Supporting information

Supporting Information

Supplementary Table S1 Parameter estimates for the pharmacokinetic model describing RS1 exposure in terms of plasma concentration.

Supplementary Material A

Supplementary Figure S1 Simulated median exposure profiles based on a one‐compartment pharmacokinetic model using the parameter estimates from Supplementary Table S1. Doses of 10 mg/kg (red), 50 mg/kg (green), or 200 mg/kg (blue) were given on days 3, 4, 5, 6, and 7.

Supplementary Figure S2 Visual predictive checks for each of the eight treatment groups: (A) vehicle; (B) radiotherapy (2 Gy per dose); (C–E) RS1 monotherapy (10, 50, or 200 mg/kg per dose); and (F–H) combination therapy with radiation (2 Gy per dose dose) and RS1 (10, 50, or 200 mg/kg per dose). Blue lines indicate simulated 5th, 50th, and 95th percentiles from the tumor model (Eqs. 6 and 7) using parameter estimates from Table 1 and Supplementary Table S1. Colored dots represent experimental observations. Two outlier data points (24,2188) and (27,3177) are not shown in plot (F).

Supplementary Figure S3 Visual predictive checks for the pharmacokinetic model for RS1 exposure. The following dose groups are represented: (A) 25 mg/kg, (B) 10 mg/kg, (C) 50 mg/kg, (D) 200 mg/kg, and (E) 100 mg/kg. Blue curves indicate simulated 5th, 50th, and 95th percentiles. Dots represent measured plasma concentrations.

Supplementary Figure S4 Simulation of the tumor model in Eq. 6 for three different exposures on the TSE curve: radiotherapy (2.17 Gy), RS1 monotherapy (400 mg/kg), and combination therapy (0.67 Gy and 48 mg/kg). Parameter estimates were taken from Table 1 and Supplementary Table S1.

Sample Code