Figure 11. Different magnetic relaxation modes.

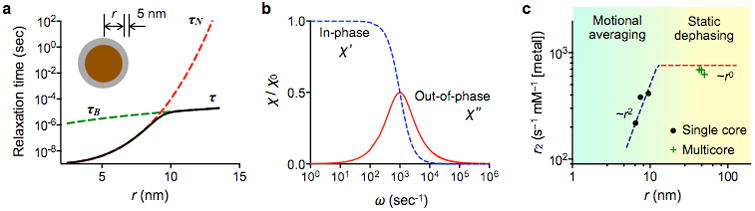
(a) An ensemble MNPs in solution can lose net magnetic moments through Neel and Brownian relaxation mechanisms. The Neel relaxation, namely the spontaneous flipping of magnetic moments inside a particle, is dominant for small MNPs. The Brown relaxation, caused by the physical rotation of particles, takes over as the particle size increases. Shown here are the Neel (τ_N) and the Brownian (τ_B) relaxation times calculated for Fe₃O4 MNPs with 5-nm surface coating. The effective relaxation time (τ) can be obtained from 1/τ_N= 1/τ_N + 1/τ_B. (b) The alternating current (AC) magnetic susceptibility has two components, the in-phase and the 90° out-of-phase with respect to the AC excitation source. The out-of-phase component has its maximum when the excitation frequency is close to the relaxation time of the particle. (c) In the NMR detection, MNPs accelerate the transverse relaxation of ¹H signal. The transverse relaxivity (r₂) is the capacity of MNPs to shorten the transverse relaxation time. The r₂ values of single and multicore MnFe₂O₄ MNPs were measured. While the r₂ values of single core MNPs increased steeply with increasing particle size (∼r²), the r₂ values for multicore MNPs showed little dependence on particle size (∼r⁰). Theoretical modeling, based on motional averaging and static dephasing, accurately describes the observed r₂-behavior (dotted lines): due to their small particle size, single-core MNPs are in the motional averaging regime (blue line), whereas multicore MNPs fall into the static dephasing regime (horizontal red line).