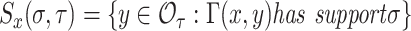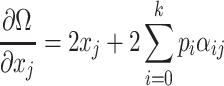Summary
Evolutionary relationships are represented by phylogenetic trees, and a phylogenetic
analysis of gene sequences typically produces a collection of these trees, one for each
gene in the analysis. Analysis of samples of trees is difficult due to the
multi-dimensionality of the space of possible trees. In Euclidean spaces, principal
component analysis is a popular method of reducing high-dimensional data to a
low-dimensional representation that preserves much of the sample’s structure. However, the
space of all phylogenetic trees on a fixed set of species does not form a Euclidean vector
space, and methods adapted to tree space are needed. Previous work introduced the notion
of a principal geodesic in this space, analogous to the first principal component. Here we
propose a geometric object for tree space similar to the  th
principal component in Euclidean space: the locus of the weighted Fréchet mean of
th
principal component in Euclidean space: the locus of the weighted Fréchet mean of
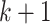 vertex trees when the weights vary over
the
vertex trees when the weights vary over
the 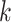 -simplex. We establish some basic properties
of these objects, in particular showing that they have dimension
-simplex. We establish some basic properties
of these objects, in particular showing that they have dimension 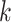 , and
propose algorithms for projection onto these surfaces and for finding the principal locus
associated with a sample of trees. Simulation studies demonstrate that these algorithms
perform well, and analyses of two datasets, containing Apicomplexa and African coelacanth
genomes respectively, reveal important structure from the second principal components.
, and
propose algorithms for projection onto these surfaces and for finding the principal locus
associated with a sample of trees. Simulation studies demonstrate that these algorithms
perform well, and analyses of two datasets, containing Apicomplexa and African coelacanth
genomes respectively, reveal important structure from the second principal components.
Keywords: Fréchet mean, Phylogenetic tree, Principal component analysis, Tree space
1. Introduction
A great opportunity offered by modern genomics is that phylogenetics applied on a genomic scale, or phylogenomics, should be especially powerful for elucidating gene and genome evolution, relationships among species and populations, and processes of speciation and molecular evolution. However, a well-recognized hurdle is the sheer volume of genomic data that can now be generated relatively cheaply and quickly, but for which analytical tools are lacking. There is a major need to explore new approaches that will enable us to undertake comparative genomic and phylogenomic studies much more rapidly and robustly than existing tools allow.
Datasets consisting of collections of phylogenetic trees are challenging to analyse, due to
their high dimensionality and the complexity of the space containing the data. Multivariate
statistical procedures such as outlier detection (Weyenberg
et al., 2014), clustering (Gori et al., 2016)
and multi-dimensional scaling (Hillis et al., 2005)
have previously been applied to such datasets, but principal component analysis is perhaps
the most useful multivariate statistical tool for exploring high-dimensional datasets. For
example, Zha et al. (2001) and Ding & He (2004) showed that principal component analysis
automatically projects to the subspace where the global solution of
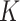 -means clustering lies, and so facilitates
-means clustering lies, and so facilitates
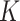 -means clustering to find near-optimal
solutions. Although principal component analysis for data in
-means clustering to find near-optimal
solutions. Although principal component analysis for data in 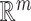 can be defined in several
different ways, the following description is natural for reformulating the procedure in tree
space. Suppose we have data
can be defined in several
different ways, the following description is natural for reformulating the procedure in tree
space. Suppose we have data 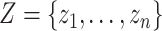 where
where
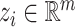 for
for
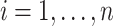 . For any set of
. For any set of
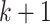 points
points 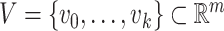 we
can define
we
can define
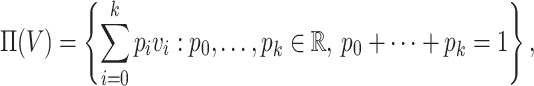 |
(1) |
so that 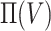 is the affine subspace of
is the affine subspace of
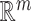 containing
containing
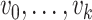 . The orthogonal
. The orthogonal
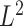 distance of any point
distance of any point
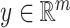 from
from
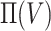 is denoted by
is denoted by
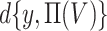 , and the sum of squared
projected distances of the data
, and the sum of squared
projected distances of the data 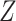 onto
onto 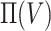 is
denoted by
is
denoted by
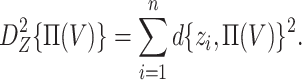 |
Then the 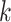 th principal component
th principal component
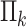 corresponds to a choice of
corresponds to a choice of
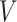 which minimizes this sum. In
which minimizes this sum. In
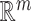 ,
, 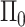 is
the sample mean,
is
the sample mean, 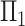 is the line through the sample mean
which minimizes the sum of squared projected distances, and so on for
is the line through the sample mean
which minimizes the sum of squared projected distances, and so on for
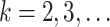 . Although it is not explicit in
the definition above, in
. Although it is not explicit in
the definition above, in 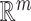 the principal components are
nested, i.e.,
the principal components are
nested, i.e., 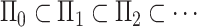 .
This description of principal component analysis relies heavily on the vector space
properties of
.
This description of principal component analysis relies heavily on the vector space
properties of  :
: 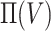 is
defined as a linear combination of vectors and the procedure uses orthogonal projection.
is
defined as a linear combination of vectors and the procedure uses orthogonal projection.
However, the space of phylogenetic trees on a fixed set of leaves is not a Euclidean vector
space, so we cannot directly apply classical principal component analysis to a dataset of
phylogenetic trees. Instead, Billera et al. (2001)
showed that the set 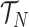 of all phylogenetic trees
with
of all phylogenetic trees
with 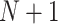 leaves labelled
leaves labelled 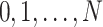 forms a
CAT
forms a
CAT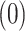 space as defined by Bridson & Haefliger (2011, Definition II.1.1). In
CAT
space as defined by Bridson & Haefliger (2011, Definition II.1.1). In
CAT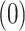 spaces any pair of points are joined by a
unique geodesic, or shortest-length path, and an algorithm exists that computes
spaces any pair of points are joined by a
unique geodesic, or shortest-length path, and an algorithm exists that computes
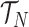 geodesics in
geodesics in
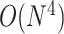 steps (Owen & Provan, 2011). Furthermore, projection onto closed sets is well defined
in CAT
steps (Owen & Provan, 2011). Furthermore, projection onto closed sets is well defined
in CAT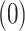 spaces.
spaces.
The analogue of the zeroth principal component is the unweighted Fréchet mean of the data
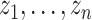 . The Fréchet mean is a
statistic which characterizes the central tendency of a distribution in arbitrary metric
spaces. For any metric space
. The Fréchet mean is a
statistic which characterizes the central tendency of a distribution in arbitrary metric
spaces. For any metric space 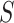 equipped with metric
equipped with metric
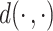 , the Fréchet population
mean
, the Fréchet population
mean 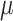 with respect to the distribution
with respect to the distribution
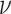 is defined by
is defined by
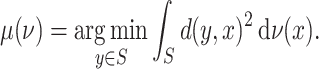 |
The discrete analogue, the weighted Fréchet mean of a sample 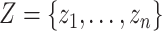 with respect to a weight
vector
with respect to a weight
vector 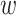 , is
, is
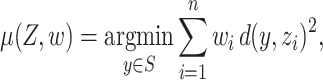 |
where the weights 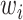 satisfy
satisfy
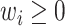 for
for 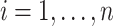 . In any
CAT
. In any
CAT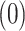 space,
space, 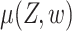 is
a well-defined unique point given data
is
a well-defined unique point given data 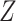 and weight vector
and weight vector
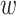 . The definition of the zeroth principal
component
. The definition of the zeroth principal
component 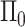 in
in 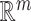 given above coincides with the
definition of the Fréchet sample mean with weights
given above coincides with the
definition of the Fréchet sample mean with weights 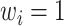 in
any CAT
in
any CAT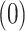 space. Several algorithms for computing
the Fréchet sample mean in
space. Several algorithms for computing
the Fréchet sample mean in 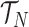 have been developed (Bačák, 2014; Miller et
al., 2015) and we review these in § 2.2,
as they play an important role in our method. The term Fréchet mean will be used throughout
to refer to a sample mean unless stated otherwise.
have been developed (Bačák, 2014; Miller et
al., 2015) and we review these in § 2.2,
as they play an important role in our method. The term Fréchet mean will be used throughout
to refer to a sample mean unless stated otherwise.
Methods for constructing a principal geodesic in tree space, an analogue of
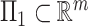 as defined above,
have recently been developed. In Nye (2011), the
approach involved firing geodesics from some mean tree. For each candidate geodesic
as defined above,
have recently been developed. In Nye (2011), the
approach involved firing geodesics from some mean tree. For each candidate geodesic
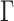 , the sum of squared projected
distances
, the sum of squared projected
distances 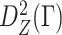 was computed and a greedy
algorithm was used to adjust
was computed and a greedy
algorithm was used to adjust 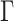 in order to minimize
in order to minimize
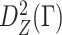 . The geodesics considered were
infinitely long, but have the disadvantage that in some cases many such geodesics fit the
data equally well. Subsequent approaches therefore considered finitely long geodesic
segments (Feragen et al., 2013; Nye, 2014). The geodesic segment between two points
. The geodesics considered were
infinitely long, but have the disadvantage that in some cases many such geodesics fit the
data equally well. Subsequent approaches therefore considered finitely long geodesic
segments (Feragen et al., 2013; Nye, 2014). The geodesic segment between two points
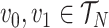 is analogous to
is analogous to
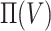 in (1) with
in (1) with 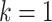 , except that the weights
, except that the weights
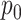 and
and 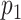 must be
constrained to be a valid probability vector; that is,
must be
constrained to be a valid probability vector; that is, 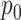 and
and
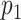 must be nonnegative and sum to 1. Feragen et al. (2013) constrained the ends of the geodesic
to be points in the sample
must be nonnegative and sum to 1. Feragen et al. (2013) constrained the ends of the geodesic
to be points in the sample 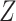 and sought the corresponding geodesic
and sought the corresponding geodesic
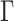 which minimizes
which minimizes
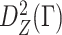 , whereas Nye (2014) did not restrict the geodesic and used a stochastic
optimization algorithm to perform the minimization.
, whereas Nye (2014) did not restrict the geodesic and used a stochastic
optimization algorithm to perform the minimization.
In this paper we address two fundamental questions: (i) which geometric object most
naturally plays the role of a 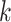 th principal component in tree space; and
(ii) given such an object, how can we efficiently project data points onto the object? Our
proposed solution is to replace the definition of
th principal component in tree space; and
(ii) given such an object, how can we efficiently project data points onto the object? Our
proposed solution is to replace the definition of 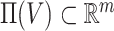 given in (1) with the locus of the
weighted Fréchet mean of points
given in (1) with the locus of the
weighted Fréchet mean of points 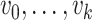 in tree space. Specifically,
suppose
in tree space. Specifically,
suppose 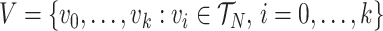 and define
and define 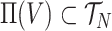 by
by
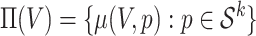 |
where 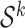 is the
is the
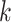 -dimensional simplex of probability vectors,
-dimensional simplex of probability vectors,
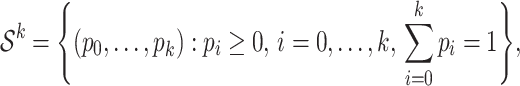 |
and 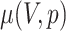 is the Fréchet mean of the points in
set
is the Fréchet mean of the points in
set 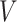 with weights
with weights 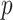 . We call
. We call
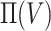 the locus of the Fréchet mean of
the locus of the Fréchet mean of
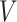 . Our choice of notation is intended to
emphasize the analogy between the definition of
. Our choice of notation is intended to
emphasize the analogy between the definition of 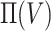 in tree space and the
corresponding definition for
in tree space and the
corresponding definition for 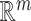 in (1). The locus of the Fréchet mean is a type
of minimal surface, as the following physical analogy suggests. Imagine connecting a point
in (1). The locus of the Fréchet mean is a type
of minimal surface, as the following physical analogy suggests. Imagine connecting a point
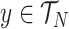 to points
to points
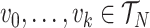 by
by
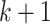 pieces of elastic. When the point
pieces of elastic. When the point
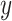 is free to move, it will move under the
action of the elastic into an equilibrium position in tree space. If the stiffness of each
piece of elastic is allowed to vary independently, corresponding to different choices for
is free to move, it will move under the
action of the elastic into an equilibrium position in tree space. If the stiffness of each
piece of elastic is allowed to vary independently, corresponding to different choices for
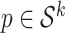 , the equilibrium point
will move about in tree space, tracing out a surface. In Euclidean space the locus of the
Fréchet mean of some collection of points is an affine subspace; however, in tree space, the
locus can be curved. Surfaces of this kind have recently been studied in the context of
Riemannian manifolds and other geodesic metric spaces (Pennec, 2015). We discuss the relationship of the present paper to that work in §
6.
, the equilibrium point
will move about in tree space, tracing out a surface. In Euclidean space the locus of the
Fréchet mean of some collection of points is an affine subspace; however, in tree space, the
locus can be curved. Surfaces of this kind have recently been studied in the context of
Riemannian manifolds and other geodesic metric spaces (Pennec, 2015). We discuss the relationship of the present paper to that work in §
6.
Our main theoretical results are as follows. First, when 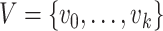 we derive a set of local
implicit equations for
we derive a set of local
implicit equations for 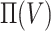 . These allow us to derive conditions
for
. These allow us to derive conditions
for 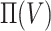 to be locally flat, and also enable us
to construct explicit realizations of
to be locally flat, and also enable us
to construct explicit realizations of 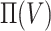 in certain cases.
Secondly, using the implicit equations we show that the locus of the Fréchet mean
in certain cases.
Secondly, using the implicit equations we show that the locus of the Fréchet mean
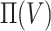 in
in 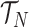 is locally
is locally
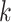 -dimensional for generic nondegenerate choices
of
-dimensional for generic nondegenerate choices
of 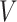 , and thus forms a suitable candidate for a
, and thus forms a suitable candidate for a
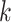 th principal component. Third, we present an
algorithm for projection onto
th principal component. Third, we present an
algorithm for projection onto 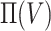 which relies only on the
CAT
which relies only on the
CAT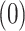 properties of
properties of 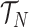 . We demonstrate accuracy of the
projection algorithm via a simulation study.
. We demonstrate accuracy of the
projection algorithm via a simulation study.
2. The geometry of tree space
2.1. Construction of tree space and its geodesics
Throughout the paper, the 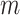 -dimensional Euclidean vector space is
denoted by
-dimensional Euclidean vector space is
denoted by 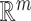 . The nonnegative and
positive orthants in
. The nonnegative and
positive orthants in 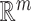 are denoted by
are denoted by
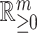 and
and
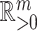 , respectively. For any
vectors
, respectively. For any
vectors 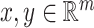 ,
,
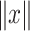 denotes the Euclidean norm of
denotes the Euclidean norm of
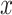 and
and 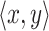 denotes the Euclidean
inner product.
denotes the Euclidean
inner product.
A phylogenetic tree with leaf set 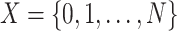 is an
undirected weighted acyclic graph with
is an
undirected weighted acyclic graph with 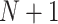 degree-
degree-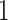 vertices labelled
vertices labelled
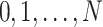 and with no
degree-
and with no
degree-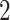 vertices. We consider rooted trees, and
the root is the leaf labelled 0. Each such tree contains
vertices. We consider rooted trees, and
the root is the leaf labelled 0. Each such tree contains 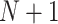 pendant edges, which connect to the leaves, and up to
pendant edges, which connect to the leaves, and up to  internal edges. The maximum number of internal edges is achieved when the tree is binary,
in which case all non-leaf vertices have degree
internal edges. The maximum number of internal edges is achieved when the tree is binary,
in which case all non-leaf vertices have degree 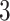 , and the tree is said
to be fully resolved. If a tree contains fewer edges, then it is said to be unresolved and
there must be at least one vertex with degree
, and the tree is said
to be fully resolved. If a tree contains fewer edges, then it is said to be unresolved and
there must be at least one vertex with degree 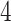 or higher. Apart from
the root edge containing taxon
or higher. Apart from
the root edge containing taxon 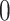 , each edge in a
phylogeny is assigned a strictly positive weight, also called the edge length. Given a
tree
, each edge in a
phylogeny is assigned a strictly positive weight, also called the edge length. Given a
tree 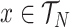 , the set of edges of
, the set of edges of
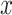 is denoted by
is denoted by 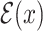 , and the weight assigned
to
, and the weight assigned
to 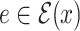 is denoted by
is denoted by
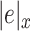 . It is convenient to define
. It is convenient to define
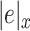 to be zero whenever
to be zero whenever
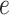 is not contained in
is not contained in
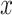 .
.
Tree space 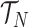 is the set of all
phylogenetic trees with leaf set
is the set of all
phylogenetic trees with leaf set 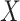 (Billera et al., 2001). Tree space can be embedded in
(Billera et al., 2001). Tree space can be embedded in
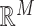 for
for
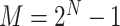 in the following way. If we cut
any edge
in the following way. If we cut
any edge 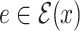 , then the tree
, then the tree
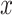 splits into two disconnected pieces. This
determines a split
splits into two disconnected pieces. This
determines a split 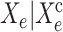 of the leaf set
of the leaf set
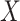 , where
, where 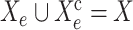 and
and
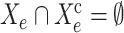 . By
convention we choose
. By
convention we choose 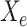 to be the set containing the root 0,
and so there are
to be the set containing the root 0,
and so there are 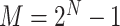 possible splits of
possible splits of
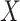 . The collection of splits represented by
a tree
. The collection of splits represented by
a tree 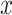 is called the topology of
is called the topology of
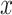 . Since edges and splits are equivalent,
we use the notation
. Since edges and splits are equivalent,
we use the notation 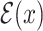 to also represent the
set of splits in
to also represent the
set of splits in 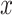 . By choosing some arbitrary ordering of
the set of all splits, each tree
. By choosing some arbitrary ordering of
the set of all splits, each tree 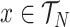 can
be represented as a vector in
can
be represented as a vector in 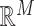 with up to
with up to
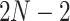 positive entries given by the edge
weights of
positive entries given by the edge
weights of 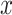 and zeros for each split that is not
contained in
and zeros for each split that is not
contained in 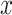 . However, an arbitrary choice of vector
will not necessarily represent a tree; for example, the splits
. However, an arbitrary choice of vector
will not necessarily represent a tree; for example, the splits 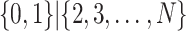 and
and
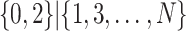 cannot both be
contained in the same tree, so any vector for which these splits both have a strictly
positive value does not represent a tree. Two splits
cannot both be
contained in the same tree, so any vector for which these splits both have a strictly
positive value does not represent a tree. Two splits 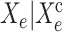 and
and
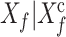 are compatible if one of
the four sets
are compatible if one of
the four sets 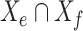 ,
, 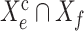 ,
,
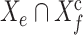 and
and
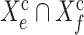 is empty,
in which case there is at least one tree containing both splits. Any collection of
pairwise compatible splits determines a valid tree topology (Semple & Steel, 2003, Theorem 3.1.4).
is empty,
in which case there is at least one tree containing both splits. Any collection of
pairwise compatible splits determines a valid tree topology (Semple & Steel, 2003, Theorem 3.1.4).
The embedding into Euclidean space reveals the combinatorial structure of
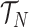 . Every tree
. Every tree
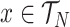 contains
contains
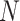 pendant edges other than the root edge,
so
pendant edges other than the root edge,
so 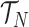 is the product of
is the product of
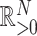 and a space
corresponding to the internal edges. It is therefore convenient to ignore the pendant
edges and consider the corresponding embedding of tree space into
and a space
corresponding to the internal edges. It is therefore convenient to ignore the pendant
edges and consider the corresponding embedding of tree space into
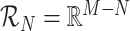 . Given
any tree topology
. Given
any tree topology 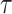 containing
containing 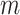 internal edges, the set of trees with topology
internal edges, the set of trees with topology 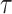 corresponds to a
subset
corresponds to a
subset 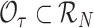 which is isomorphic to
which is isomorphic to 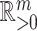 with respect to the
local Euclidean structure. Each such region is called the orthant for topology
with respect to the
local Euclidean structure. Each such region is called the orthant for topology
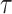 . The boundary of
. The boundary of
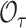 in
in
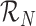 corresponds to trees obtained
by removing one or more internal edges from
corresponds to trees obtained
by removing one or more internal edges from 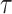 . Equivalently, the
trees on the boundary can be obtained by taking a tree
. Equivalently, the
trees on the boundary can be obtained by taking a tree 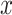 in
in
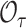 and continuously
shrinking one or more internal edges down to length zero. Thus, for a fully resolved
topology
and continuously
shrinking one or more internal edges down to length zero. Thus, for a fully resolved
topology 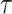 , the
codimension-
, the
codimension-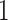 boundaries of
boundaries of 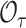 correspond to trees
containing
correspond to trees
containing 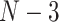 internal edges, and in general each
codimension-
internal edges, and in general each
codimension-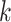 boundary corresponds to trees containing
boundary corresponds to trees containing
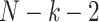 internal edges, for
internal edges, for
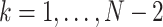 . There are
. There are
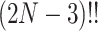 possible fully resolved rooted
tree topologies, and so
possible fully resolved rooted
tree topologies, and so 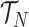 is built from
is built from
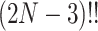 orthants isomorphic to
orthants isomorphic to
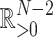 together with the
boundaries of these orthants which correspond to trees that are not fully resolved.
Orthants are glued together at their boundaries, since a given unresolved tree containing
together with the
boundaries of these orthants which correspond to trees that are not fully resolved.
Orthants are glued together at their boundaries, since a given unresolved tree containing
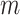 internal edges can be obtained by
removing edges from several different trees containing
internal edges can be obtained by
removing edges from several different trees containing 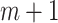 edges. Orthants corresponding to fully resolved topologies are glued at their
codimension-
edges. Orthants corresponding to fully resolved topologies are glued at their
codimension-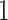 boundaries in a relatively simple way. If
a single internal edge in a tree with fully resolved topology
boundaries in a relatively simple way. If
a single internal edge in a tree with fully resolved topology 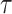 is
contracted to length zero and removed from the tree, the result is a vertex of degree
is
contracted to length zero and removed from the tree, the result is a vertex of degree
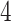 . There are three possible ways to add in
an extra edge to give a fully resolved topology, so each
codimension-
. There are three possible ways to add in
an extra edge to give a fully resolved topology, so each
codimension-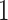 face of
face of 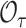 is glued to two other such
orthants. Trees containing no internal edges are called star trees; the point
is glued to two other such
orthants. Trees containing no internal edges are called star trees; the point
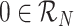 corresponds to the set of
star trees and is contained in the boundary of every orthant
corresponds to the set of
star trees and is contained in the boundary of every orthant 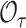 .
.
The topology of 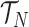 is taken to be that induced
by the embedding into Euclidean space. Geodesics are constructed by considering continuous
paths in
is taken to be that induced
by the embedding into Euclidean space. Geodesics are constructed by considering continuous
paths in 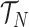 which are Euclidean
straight-line segments in each orthant. The length of a path is the sum of the Euclidean
segment lengths. As shown by Billera et al. (2001),
the shortest such path or geodesic between two points
which are Euclidean
straight-line segments in each orthant. The length of a path is the sum of the Euclidean
segment lengths. As shown by Billera et al. (2001),
the shortest such path or geodesic between two points 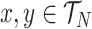 is unique, and it will
be denoted by
is unique, and it will
be denoted by 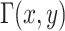 . The distance
. The distance
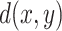 is defined to be the length of
is defined to be the length of
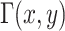 , and this defines the metric
, and this defines the metric
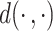 on
on
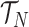 . By definition,
. By definition,
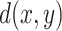 incorporates information about both
the topologies and the edge lengths of
incorporates information about both
the topologies and the edge lengths of 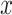 and
and
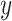 . Given two points
. Given two points
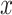 and
and 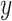 in the
same orthant,
in the
same orthant, 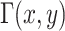 is simply the Euclidean line
segment between
is simply the Euclidean line
segment between 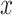 and
and 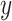 ,
whereas when
,
whereas when 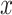 and
and 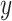 are in
different orthants,
are in
different orthants, 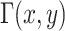 consists of a series of
straight-line segments traversing orthants corresponding to different topologies. Billera et al. (2001) proved that
consists of a series of
straight-line segments traversing orthants corresponding to different topologies. Billera et al. (2001) proved that
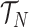 is a
CAT
is a
CAT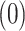 space, so it has several additional
geometrical properties (Bridson & Haefliger,
2011).
space, so it has several additional
geometrical properties (Bridson & Haefliger,
2011).
Owen & Provan (2011) established an
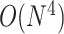 algorithm to compute the geodesic
between any two trees in
algorithm to compute the geodesic
between any two trees in 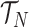 . The details of their
algorithm are not important for the present application, but we do require some notation
for the form of the geodesics it constructs. Given
. The details of their
algorithm are not important for the present application, but we do require some notation
for the form of the geodesics it constructs. Given 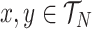 , let
, let
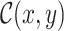 be the set of splits in
be the set of splits in
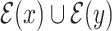 which are compatible with every split in
which are compatible with every split in 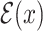 and
every split in
and
every split in 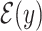 . Adopting notation from
Owen & Provan (2011), the geodesic
. Adopting notation from
Owen & Provan (2011), the geodesic
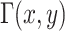 is characterized by disjoint
sets of internal splits
is characterized by disjoint
sets of internal splits
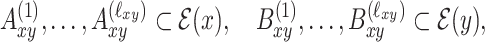 |
where  is an integer that depends
on
is an integer that depends
on  and
and  . These
sets of splits determine the order in which edges are removed and added as the geodesic is
traversed; the
. These
sets of splits determine the order in which edges are removed and added as the geodesic is
traversed; the 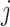 th topology visited contains splits
th topology visited contains splits
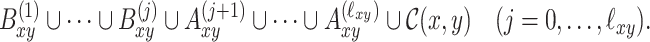 |
The union 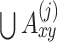
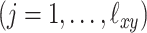 is
is
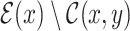 and similarly for tree
and similarly for tree 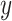 . We let
. We let 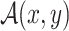 be the ordered list of sets
be the ordered list of sets
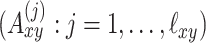 and
similarly define
and
similarly define 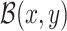 . The support of
. The support of
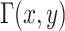 , defined to be the triple
, defined to be the triple
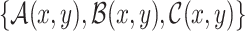 ,
characterizes the sequence of orthants the geodesic traverses. For any set
,
characterizes the sequence of orthants the geodesic traverses. For any set
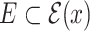 we adopt the
notation
we adopt the
notation
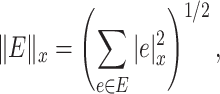 |
and similarly for subsets of 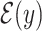 . Owen & Provan (2011) showed that
. Owen & Provan (2011) showed that
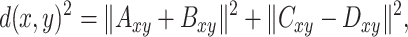 |
(2) |
where 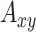 is the
is the 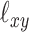 -dimensional vector whose
-dimensional vector whose
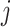 th element is
th element is 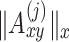 , and similarly for
, and similarly for
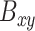 the
the 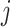 th
element is
th
element is 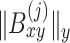 . The vectors
. The vectors
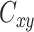 and
and 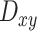 have dimension
have dimension 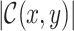 and respectively contain
the edge lengths
and respectively contain
the edge lengths  and
and 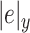 for
for 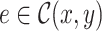 . It follows from
(2) that
. It follows from
(2) that
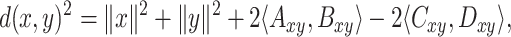 |
(3) |
where 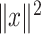 is the sum of squared edge lengths
in
is the sum of squared edge lengths
in 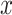 and similarly for
and similarly for
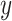 .
.
The following definition characterizes certain geodesics which behave rather like Euclidean straight lines.
Definition 1
(Simple geodesic). Suppose that
are fully resolved. The geodesic
is said to be simple if each of the sets
and
contains exactly one element for
. Equivalently,
is simple if and only if at most one edge length at a time contracts to zero as the geodesic is traversed.
The following definition determines the set of trees 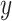 such
that the geodesics
such
that the geodesics 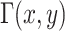 to a fixed point
to a fixed point
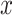 all share the same support.
all share the same support.
Definition 2
(Support region). Fix some point
and an orthant
corresponding to a fully resolved topology
. Let
be the support of
for some
. Then the set
is called a support region. The number of support regions for fixed
and
is finite since geodesics of the form
for
have finitely many distinct supports.
Miller et al. (2015) considered very similar
subsets of 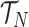 and established their
properties. This relied on a map
and established their
properties. This relied on a map 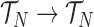 defined by squaring edge lengths. In the image of this map, Miller et al. (2015) showed that each support region is defined by a
set of linear inequalities and that the boundaries between support regions are
codimension-
defined by squaring edge lengths. In the image of this map, Miller et al. (2015) showed that each support region is defined by a
set of linear inequalities and that the boundaries between support regions are
codimension-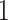 hyperplanes. It follows, by inverting the
squaring map, that the union over the set
hyperplanes. It follows, by inverting the
squaring map, that the union over the set 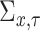 of
possible supports,
of
possible supports, 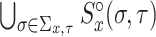 ,
is dense in
,
is dense in 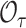 , where
, where
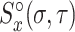 denotes the interior
of each support region; it also follows that the boundaries between the support regions
are continuous codimension-
denotes the interior
of each support region; it also follows that the boundaries between the support regions
are continuous codimension-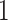 surfaces within each orthant.
surfaces within each orthant.
2.2. Algorithms for computing the Frechét mean
Several algorithms for computing the unweighted or weighted Fréchet mean of a sample in
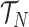 have been developed (Sturm, 2003; Bačák,
2014; Miller et al., 2015). These
algorithms have the following general structure. Suppose we have a set
have been developed (Sturm, 2003; Bačák,
2014; Miller et al., 2015). These
algorithms have the following general structure. Suppose we have a set
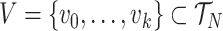 .
At the
.
At the 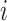 th iteration there is an estimate
th iteration there is an estimate
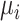 of the Fréchet mean of
of the Fréchet mean of
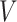 . To find the next estimate,
. To find the next estimate,
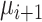 , a data point
, a data point
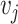 is selected, either deterministically
or stochastically depending on the particular algorithm. The geodesic
is selected, either deterministically
or stochastically depending on the particular algorithm. The geodesic
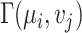 is constructed, and
is constructed, and
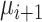 is taken to be the point a
certain proportion of the distance along the geodesic. This proportion can depend on the
weights when the weighted Fréchet mean is estimated. In each case, some form of
convergence of the sequence
is taken to be the point a
certain proportion of the distance along the geodesic. This proportion can depend on the
weights when the weighted Fréchet mean is estimated. In each case, some form of
convergence of the sequence 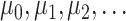 to the Fréchet
mean of
to the Fréchet
mean of 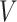 can be proved, independent of the initial
estimate
can be proved, independent of the initial
estimate 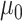 .
.
Our method does not make direct use of these algorithms. However, as described in § 4.1, our proposed algorithm for projecting data onto
the locus of the Fréchet mean is adapted from the algorithm of Sturm (2003), which computes the Fréchet mean of
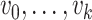 using weights
using weights
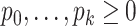 . By definition, the
Fréchet mean is invariant under positive scaling of the weights, so we can assume
. By definition, the
Fréchet mean is invariant under positive scaling of the weights, so we can assume
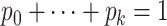 without loss of
generality. Sturm’s algorithm proceeds in the following way.
without loss of
generality. Sturm’s algorithm proceeds in the following way.
Algorithm 1.
Sturm’s algorithm for the weighted Fréchet mean.
Fix an initial estimate
and set
.
Repeat:
Sample
such that
.
Construct
.
Let
be the point a proportion
along
, where
.
Set
.
Until the sequence
converges.
Convergence can be tested in various ways, for example by repeating until a specified
number of consecutive estimates 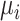 all lie within
distance
all lie within
distance 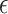 of each other. Sturm proved that
the points
of each other. Sturm proved that
the points 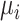 converge in probability to the
Fréchet mean of the distribution defined by sampling
converge in probability to the
Fréchet mean of the distribution defined by sampling 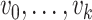 according to probabilities
according to probabilities
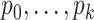 .
.
The deterministic algorithm of Bačák (2014) for
computing the weighted Fréchet mean is similar to Sturm’s algorithm, except that the data
points are used cyclically, as opposed to being randomly sampled, and the weighting is
instead taken into account in the definition of the proportions 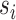 . We
use the algorithm of Bačák (2014) for computing the
Fréchet mean in order to test our projection algorithm, and this procedure is also
described in § 4.1.
. We
use the algorithm of Bačák (2014) for computing the
Fréchet mean in order to test our projection algorithm, and this procedure is also
described in § 4.1.
2.3. Convex hulls
Nye (2014) suggested that the convex hull of
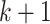 points in
points in 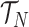 might be a suitable
geometrical object to represent a
might be a suitable
geometrical object to represent a 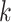 th principal component.
A set
th principal component.
A set 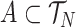 is convex if and
only if for all points
is convex if and
only if for all points 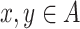 the geodesic
the geodesic
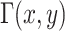 is also contained in
is also contained in
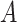 . The convex hull of a set of points is
the smallest convex set containing those points. Any geodesic segment is the convex hull
of its endpoints, and using the convex hull of three points to represent a second
principal component is a natural generalization of the idea of a principal geodesic.
Convexity is also a desirable property when performing projections, as occurs in principal
component analysis. However, convex hulls in tree space do not have the correct dimension.
Examples for which the convex hull of three points is three-dimensional can readily be
constructed, as shown in a 2015 University of Kentucky PhD thesis by G. Weyenberg and in
Lubiw et al. (2017). Lin et al. (2016, § 3) show that
the dimension of a convex hull of three points in
. The convex hull of a set of points is
the smallest convex set containing those points. Any geodesic segment is the convex hull
of its endpoints, and using the convex hull of three points to represent a second
principal component is a natural generalization of the idea of a principal geodesic.
Convexity is also a desirable property when performing projections, as occurs in principal
component analysis. However, convex hulls in tree space do not have the correct dimension.
Examples for which the convex hull of three points is three-dimensional can readily be
constructed, as shown in a 2015 University of Kentucky PhD thesis by G. Weyenberg and in
Lubiw et al. (2017). Lin et al. (2016, § 3) show that
the dimension of a convex hull of three points in 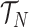 can be arbitrarily high as
can be arbitrarily high as
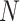 increases. More generally, convex hulls
in tree space are difficult to characterize geometrically, and several fundamental
questions remain unanswered. These issues make convex hulls less appealing as geometrical
objects to represent principal components, so we focus our attention on the locus of the
Fréchet mean. We shall, however, demonstrate the relationship between the locus of the
Fréchet mean and the convex hull for an explicit configuration of three points
increases. More generally, convex hulls
in tree space are difficult to characterize geometrically, and several fundamental
questions remain unanswered. These issues make convex hulls less appealing as geometrical
objects to represent principal components, so we focus our attention on the locus of the
Fréchet mean. We shall, however, demonstrate the relationship between the locus of the
Fréchet mean and the convex hull for an explicit configuration of three points
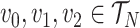 later in §
3.4.
later in §
3.4.
3. The locus of the Fréchet mean
3.1. Basic properties
Throughout this section we work with 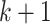 vertex points
vertex points
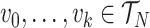 and let
and let
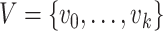 . As in § 1, we define
. As in § 1, we define 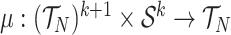 by
by
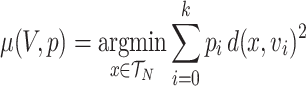 |
and denote the associated locus of the Fréchet mean by
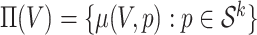 .
.
Here we establish some basic properties of  , while § 3.2 presents a more detailed analysis of
, while § 3.2 presents a more detailed analysis of
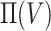 within orthant interiors. First, the
map
within orthant interiors. First, the
map 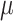 is continuous and so
is continuous and so
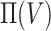 is compact, since it is the
continuous image of a compact set. Continuity of
is compact, since it is the
continuous image of a compact set. Continuity of 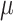 can
be proved using the deterministic algorithm for calculating the weighted Fréchet mean
given by Bačák (2014); the output of the algorithm
depends continuously on the inputs
can
be proved using the deterministic algorithm for calculating the weighted Fréchet mean
given by Bačák (2014); the output of the algorithm
depends continuously on the inputs 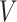 and
and
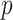 . Secondly, the points
. Secondly, the points
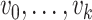 are contained in
are contained in
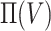 , since
, since 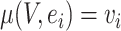 where
where
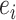 denotes the
denotes the 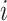 th
standard basis vector in
th
standard basis vector in 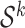 . Similarly, each geodesic
. Similarly, each geodesic
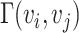 is contained in
is contained in
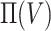 , by taking
, by taking 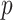 to be
a convex combination of
to be
a convex combination of 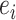 and
and 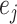 . By
the same argument, if
. By
the same argument, if 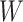 is a nonempty subset of
is a nonempty subset of
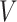 , then
, then 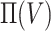 contains
contains 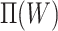 .
.
In Euclidean space the convex hull of  points coincides with
the locus of the Fréchet mean of the points. However, this is not the case in tree space,
though
points coincides with
the locus of the Fréchet mean of the points. However, this is not the case in tree space,
though 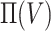 is contained in the closure of the
convex hull of
is contained in the closure of the
convex hull of 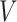 . This latter property follows because any
point in
. This latter property follows because any
point in 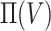 can be approximated arbitrarily
closely by performing a finite number of steps in the algorithm of Bačák (2014), as shown in § 2.2. Provided the algorithm is initialized with one of the points
can be approximated arbitrarily
closely by performing a finite number of steps in the algorithm of Bačák (2014), as shown in § 2.2. Provided the algorithm is initialized with one of the points
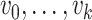 , each of these steps remains
within the convex hull, and so the limit point is contained in the closure of the convex
hull. Note that
, each of these steps remains
within the convex hull, and so the limit point is contained in the closure of the convex
hull. Note that 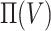 is itself generally not convex, so
there may not be a unique closest point on
is itself generally not convex, so
there may not be a unique closest point on 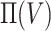 to any given point
to any given point
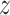 , although the minimum distance of
, although the minimum distance of
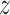 from
from 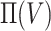 is well defined. By using
is well defined. By using 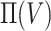 as a principal component we have
therefore lost the desirable property of uniqueness of projection.
as a principal component we have
therefore lost the desirable property of uniqueness of projection.
Fréchet means in tree space exhibit a property called stickiness (Hotz et al., 2013). This essentially means that for fixed
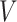 the map
the map 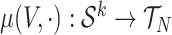 can fail to be injective. Specifically, depending on the points in
can fail to be injective. Specifically, depending on the points in
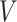 , there may exist open sets in
, there may exist open sets in
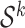 which all map to the same
point in tree space. This has implications when we project data points onto
which all map to the same
point in tree space. This has implications when we project data points onto
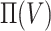 : given a data point
: given a data point
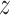 , the value of
, the value of 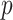 which
minimizes
which
minimizes 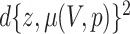 might be nonunique, even
if there is a unique closest point
might be nonunique, even
if there is a unique closest point 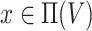 to
to
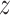 .
.
3.2. Implicit equations for the locus of the Fréchet mean
The algebraic form of tree space geodesics described in § 2.1 can be used to derive implicit equations for the edge lengths of
trees lying on the locus of the Fréchet mean 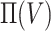 , and these
equations are fundamental to establishing the dimension of
, and these
equations are fundamental to establishing the dimension of 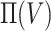 .
For fixed
.
For fixed 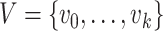 , consider the
objective function
, consider the
objective function 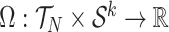 defined by
defined by
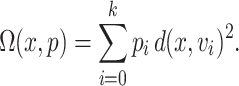 |
Suppose we fix an orthant 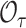 for a fully resolved
topology
for a fully resolved
topology  . Let
. Let 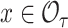 have edge lengths
have edge lengths
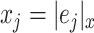 where
where 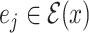
 . Miller et al. (2015) showed that functions of the form
. Miller et al. (2015) showed that functions of the form
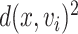 are continuously differentiable
on
are continuously differentiable
on 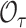 with respect to the edge
lengths
with respect to the edge
lengths 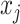 . In order to minimize
. In order to minimize
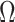 we also assume that
we also assume that
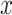 lies in a set
lies in a set
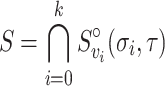 |
(4) |
for some choice of supports 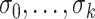 .
We call sets of this form mutual support regions with respect to
.
We call sets of this form mutual support regions with respect to 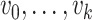 . For each
. For each
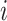 the sets
the sets 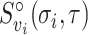 are open and
the union over possible choices
are open and
the union over possible choices 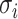 is dense in
is dense in
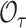 , as shown in § 2.1. Since the intersection of finitely many dense
open sets is also dense, it follows that the union of sets of the form
, as shown in § 2.1. Since the intersection of finitely many dense
open sets is also dense, it follows that the union of sets of the form
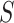 in (4) over all choices
in (4) over all choices 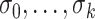 is dense in
is dense in 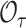 . Each mutual support
region is essentially a piece of tree space for which the combinatorics of the geodesics
to
. Each mutual support
region is essentially a piece of tree space for which the combinatorics of the geodesics
to  do not vary as a reference
point moves around the region. An example of a decomposition of orthants into mutual
support regions is given in § 3.4. Under this
assumption on
do not vary as a reference
point moves around the region. An example of a decomposition of orthants into mutual
support regions is given in § 3.4. Under this
assumption on 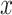 , we can write down the algebraic form of
, we can write down the algebraic form of
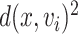 using (3), to give
using (3), to give
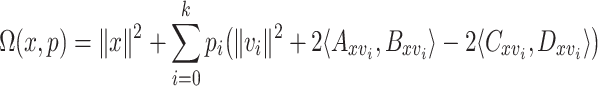 |
so that
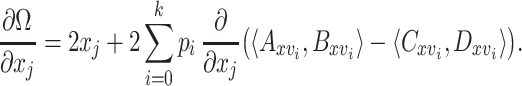 |
(5) |
If the point 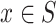 lies on the locus of the Fréchet
mean
lies on the locus of the Fréchet
mean 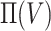 , then
, then 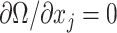 for all
for all
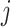 , and so we want to evaluate these
derivatives to obtain implicit equations relating the edge lengths
, and so we want to evaluate these
derivatives to obtain implicit equations relating the edge lengths
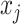 to the vector
to the vector 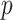 .
.
Let 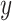 be any of the trees
be any of the trees
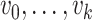 . By definition,
. By definition,
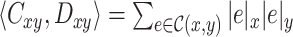 ,
so
,
so
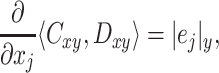 |
since 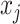 is the length of split
is the length of split
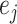 . The derivative of
. The derivative of
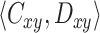 is therefore
a constant. The term
is therefore
a constant. The term  has a more
general functional dependence on
has a more
general functional dependence on 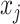 . By definition,
. By definition,
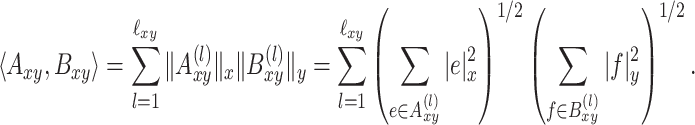 |
For any edge 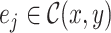 this expression does
not depend on
this expression does
not depend on 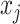 , so the derivative is zero. When
, so the derivative is zero. When
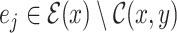 ,
only the first term in brackets will depend on
,
only the first term in brackets will depend on 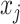 . Since the sets
. Since the sets
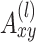 are disjoint, it must be the
case that
are disjoint, it must be the
case that 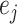 is contained in exactly one set, and we
define
is contained in exactly one set, and we
define 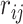 to be the index
to be the index
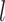 of that set when
of that set when
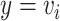 . Then
. Then
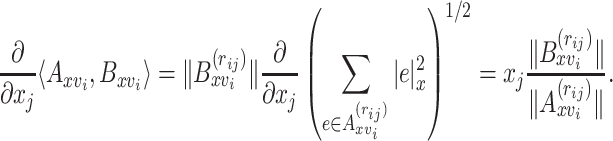 |
In the case where 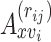 contains only
contains only
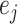 and no other splits, we have
and no other splits, we have
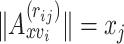 , so the
expression becomes
, so the
expression becomes 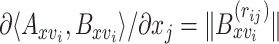 ,
which is also a constant. Substituting these expressions into (5) gives
,
which is also a constant. Substituting these expressions into (5) gives
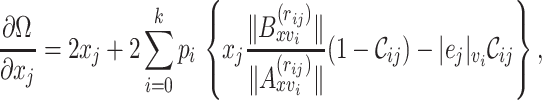 |
(6) |
where 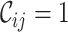 if
if
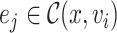 and 0
otherwise.
and 0
otherwise.
We define 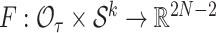 by
by
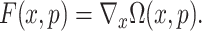 |
(7) |
Miller et al. (2015) showed that the function
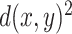 for fixed
for fixed
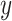 is continuously differentiable on
is continuously differentiable on
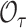 with respect to
with respect to
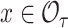 . Higher derivatives
exist within each support region
. Higher derivatives
exist within each support region 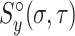 .
It follows that
.
It follows that 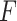 is continuously differentiable with
respect to the edge lengths for all
is continuously differentiable with
respect to the edge lengths for all 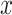 lying within the
interior of mutual support regions, and that
lying within the
interior of mutual support regions, and that  is continuous on
is continuous on
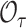 . However,
. However,
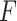 may not be differentiable on the boundary
between mutual support regions. In § 3.3 we show
that the matrix of second derivatives of
may not be differentiable on the boundary
between mutual support regions. In § 3.3 we show
that the matrix of second derivatives of 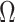 is positive
definite on each mutual support region, and so every solution to
is positive
definite on each mutual support region, and so every solution to 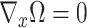 is a minimum. It follows
that
is a minimum. It follows
that 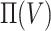 is locally the solution to
is locally the solution to
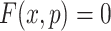 .
.
The following lemma establishes conditions for 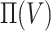 to be a flat
affine subspace within the mutual support region
to be a flat
affine subspace within the mutual support region 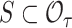 .
.
Lemma 1.
If the supports
are such that the geodesics
are simple for all
, in the sense of Definition 1, then
is an affine subspace of dimension
or lower in
.
Proof.
If all the geodesics
are simple for
, then each set
contains exactly one split. Then (6) becomes
for some constants
. Solving
gives each edge length
as a linear combination of
, which establishes the result. Generically,
is therefore locally a
-dimensional affine subspace of
, but the dimension may be lower. Further discussion of the dimension is given in § 3.3. □
3.3. The dimension of the locus of the Fréchet mean
That 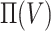 has dimension
has dimension
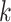 in each mutual support region follows
quickly from the form of
in each mutual support region follows
quickly from the form of 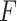 in (7) through application of the implicit function theorem.
in (7) through application of the implicit function theorem.
Lemma 2.
The matrix with elements
is positive definite for all
in mutual support region
.
A proof of this lemma can be found in the Supplementary Material.
Theorem 1.
Within the mutual support region
, the locus of the Fréchet mean
is a submanifold of dimension
or lower. For generic selections of the points
, the dimension is
.
Proof.
Application of the implicit function theorem to the map
when
establishes that there is a locally defined function
such that
and that the locus
is a
-dimensional submanifold of
. In fact, the image
will be
-dimensional when
, the derivative of
with respect to
, has rank
, which holds for generic selections of
in tree space. This is analogous to considering the unique affine subspace containing
given points in Euclidean space: generically the subspace has dimension
, but it can be lower. □
3.4. Explicit calculation
In this subsection we construct an explicit example of the locus of the Fréchet mean for
three points in 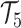 . This example helps to
demonstrate the nature of geodesics in tree space, the derivation of the implicit
equations for
. This example helps to
demonstrate the nature of geodesics in tree space, the derivation of the implicit
equations for 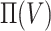 , the relationship with the convex
hull, and other geometrical features. We start by fixing
, the relationship with the convex
hull, and other geometrical features. We start by fixing 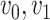 and
and 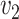 to have the topologies and edge lengths
shown in Fig. 1(a). We will ignore the pendant edge
lengths, and so the orthants containing these trees can be identified with three orthants
in
to have the topologies and edge lengths
shown in Fig. 1(a). We will ignore the pendant edge
lengths, and so the orthants containing these trees can be identified with three orthants
in 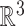 equipped with standard
coordinates
equipped with standard
coordinates 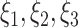 . There are five splits
contained in these trees, excluding the pendant splits; they will be written as
. There are five splits
contained in these trees, excluding the pendant splits; they will be written as
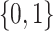 ,
, 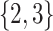 ,
,
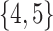 ,
, 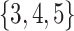 and
and 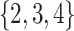 by neglecting the complements in
by neglecting the complements in
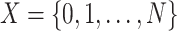 . We then let
. We then let
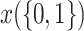 denote the length associated
with split
denote the length associated
with split 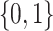 in tree
in tree 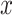 , for
example. Under the identification with
, for
example. Under the identification with 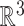 we have
we have
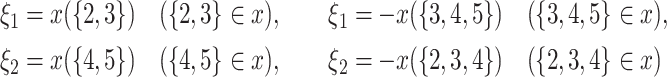 |
and 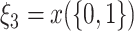 . Figure 1(b) shows the location of trees
. Figure 1(b) shows the location of trees 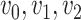 under this identification. The
orthant
under this identification. The
orthant 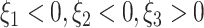 does not
correspond to a valid tree topology as
does not
correspond to a valid tree topology as 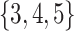 is not
compatible with
is not
compatible with 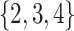 . At each
codimension-
. At each
codimension- face between the orthants shown there is
in fact a third orthant in
face between the orthants shown there is
in fact a third orthant in  glued at the same boundary,
but these orthants do not play a role in this example.
glued at the same boundary,
but these orthants do not play a role in this example.
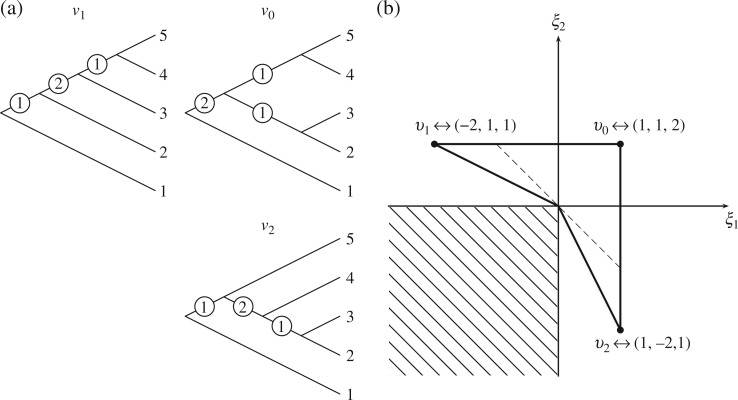
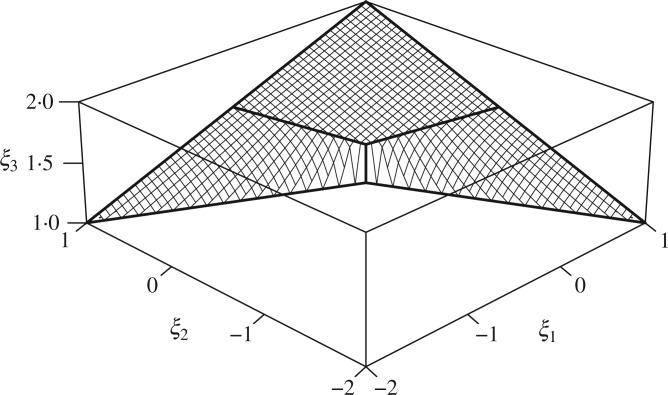
Fig. 1.
(a) Topologies for the trees 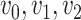 of the
example in § 3.4; the circled numbers are
weights for internal edges. (b) Coordinates of the trees
of the
example in § 3.4; the circled numbers are
weights for internal edges. (b) Coordinates of the trees 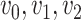 under the identification with
orthants in
under the identification with
orthants in 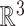 ; the
; the
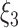 axis points out of the page. The
geodesics between
axis points out of the page. The
geodesics between 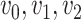 are shown:
are shown:
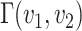 kinks around the
origin; the dashed line is between points
kinks around the
origin; the dashed line is between points 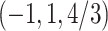 and
and
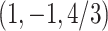 on
on 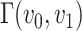 and
and
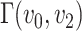 , respectively; the
lower left quadrant does not correspond to any tree topology, and is not a part of the
space.
, respectively; the
lower left quadrant does not correspond to any tree topology, and is not a part of the
space.
In Fig. 1(b) it can be seen that the geodesics
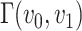 and
and
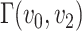 are straight-line segments
under the identification with
are straight-line segments
under the identification with  , while the
geodesic
, while the
geodesic 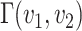 kinks at a
codimension-
kinks at a
codimension-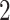 face. This behaviour is typical of
geodesics in
face. This behaviour is typical of
geodesics in 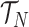 : they are straight-line
segments within each orthant but can contain kinks at the boundaries between orthants.
Figure 1(b) also shows how the convex hull of
: they are straight-line
segments within each orthant but can contain kinks at the boundaries between orthants.
Figure 1(b) also shows how the convex hull of
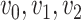 has dimension 3. The dashed
line shows the geodesic between points
has dimension 3. The dashed
line shows the geodesic between points 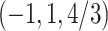 and
and
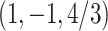 on
on 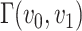 and
and 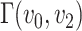 , respectively. The convex
hull therefore contains the points
, respectively. The convex
hull therefore contains the points 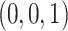 and
and
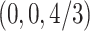 , so there are four points which
are not coplanar within each orthant of the convex hull.
, so there are four points which
are not coplanar within each orthant of the convex hull.
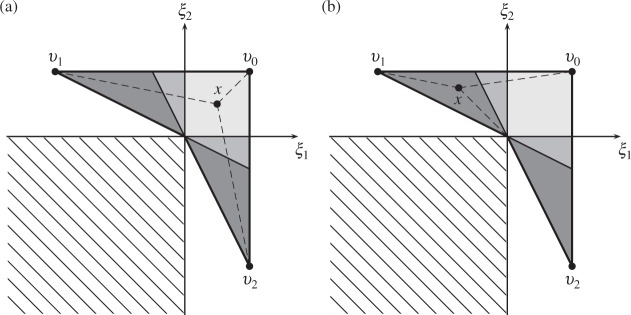
Figure 2 shows the decomposition of the orthants into
mutual support regions for 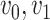 and
and 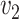 .
There are five regions in total, and the geodesics
.
There are five regions in total, and the geodesics  are simple for all
are simple for all
 when
when  is
contained in three of the regions. Lemma 1 shows that
is
contained in three of the regions. Lemma 1 shows that  is therefore planar in those regions with equation
is therefore planar in those regions with equation
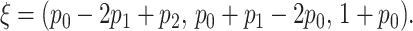 |
Fig. 2.
Decomposition of the locus of the Fréchet mean into mutual support regions. There are
five such regions, represented by shading: two mutual support regions are dark grey,
and two are mid-grey. The dashed lines show the geodesics between a point
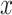 and the points
and the points
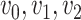 : (a) when
: (a) when
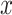 is contained in the light grey mutual
support region, none of the geodesics
is contained in the light grey mutual
support region, none of the geodesics 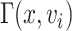 hit
codimension-
hit
codimension-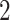 orthant faces, so Lemma 1 shows that
orthant faces, so Lemma 1 shows that
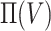 is planar within the region; the
same applies to the two mutual support regions shaded mid-grey; (b) when
is planar within the region; the
same applies to the two mutual support regions shaded mid-grey; (b) when
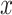 is contained in one of the dark grey
shaded regions, then
is contained in one of the dark grey
shaded regions, then 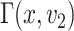 is not simple as it
intersects a codimension-
is not simple as it
intersects a codimension-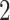 boundary, so the part of
boundary, so the part of
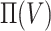 lying within this region is not
planar.
lying within this region is not
planar.
We can also explicitly calculate equations for 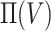 in the mutual
support region contained in
in the mutual
support region contained in 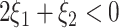 and shown in dark grey at
the top-left of each panel in Fig. 2. For
and shown in dark grey at
the top-left of each panel in Fig. 2. For
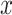 contained in this region, the squared
distances to the vertices are
contained in this region, the squared
distances to the vertices are
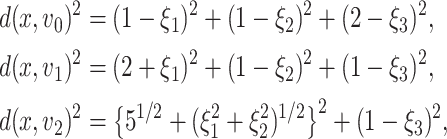 |
where 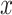 has coordinates
has coordinates 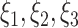 . These can be used to write
down an equation for
. These can be used to write
down an equation for 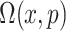 , and then (6) becomes
, and then (6) becomes
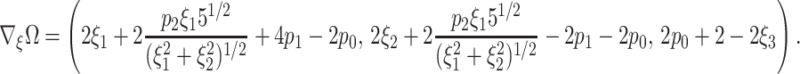 |
Then 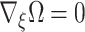 can be solved to give
can be solved to give
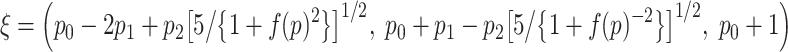 |
whenever 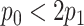 , where
, where 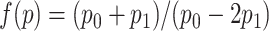 . The resulting
surface is shown in Fig. 3, from which we can see
that
. The resulting
surface is shown in Fig. 3, from which we can see
that 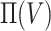 forms a nonconvex two-dimensional
surface that is contained within the convex hull.
forms a nonconvex two-dimensional
surface that is contained within the convex hull.
Fig. 3.
Perspective view of 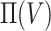 for the example in § 3.4. The locus of the Fréchet mean is a
two-dimensional surface which resembles a rubber sheet pulled taut between the
corners.
for the example in § 3.4. The locus of the Fréchet mean is a
two-dimensional surface which resembles a rubber sheet pulled taut between the
corners.
4. Projection onto the locus of the Fréchet mean and principal component analysis
4.1. Projection
In order to use the surface 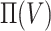 as a principal component, we need to
be able to project data onto
as a principal component, we need to
be able to project data onto 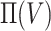 . Let
. Let 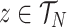 denote a data point and
fix
denote a data point and
fix 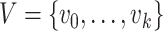 . A projection of
. A projection of
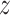 onto
onto 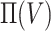 is a point which minimizes
is a point which minimizes 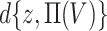 . This point may not be unique
as
. This point may not be unique
as 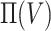 is not convex. A naive algorithm to
find a projection is to perform an exhaustive search, as described in Algorithm 2.
is not convex. A naive algorithm to
find a projection is to perform an exhaustive search, as described in Algorithm 2.
Algorithm 2.
Exhaustive search to project
onto
.
Construct a lattice of points
. For
this is a triangular lattice.
For each point
use a standard algorithm to compute
.
Find
which minimizes
.
We implemented this algorithm for 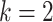 and used the
algorithm of Bačák (2014) in the second step to
compute Fréchet means. Algorithm 2 is computationally very expensive, since the resolution
of the lattice
and used the
algorithm of Bačák (2014) in the second step to
compute Fréchet means. Algorithm 2 is computationally very expensive, since the resolution
of the lattice 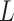 needs to be quite fine in order to obtain
accurate results. Consequently we use the exhaustive search algorithm only as a benchmark
for assessing other methods.
needs to be quite fine in order to obtain
accurate results. Consequently we use the exhaustive search algorithm only as a benchmark
for assessing other methods.
We would like a more efficient algorithm defined entirely in terms of the geodesic geometry, since any reliance on local differentiable structure is likely to be problematic at orthant boundaries. We propose Algorithm 3, which we call the geometric projection algorithm.
Algorithm 3.
Geometric projection algorithm to project
onto
.
Fix an initial estimate
of the projection of
, let
, and set
.
Repeat:
Construct
for
.
For
let
be the point a proportion
along
.
Find
which minimizes
.
Set
and
, where
is the
th standard basis vector
in
.
Set
.
Until the sequence
converges.
Algorithm 3 is a modification of Sturm’s algorithm for computing the Fréchet mean of
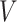 , Algorithm 1. At each step of Sturm’s
algorithm, one of the points
, Algorithm 1. At each step of Sturm’s
algorithm, one of the points 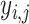 is used as the new estimate
is used as the new estimate
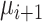 , and the point
, and the point
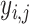 is sampled according to a fixed
probability vector
is sampled according to a fixed
probability vector 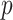 . Here, the new estimate for the
projection,
. Here, the new estimate for the
projection, 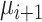 , is again chosen from
, is again chosen from
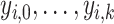 but is selected to
greedily minimize the distance from
but is selected to
greedily minimize the distance from 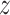 . The vector
. The vector
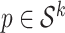 estimates the weight
vector associated with the projected point: at iteration
estimates the weight
vector associated with the projected point: at iteration 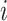 ,
,
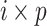 is a vector with integer
entries which counts the number of times the algorithm has moved the estimate of the
projection towards each vertex in
is a vector with integer
entries which counts the number of times the algorithm has moved the estimate of the
projection towards each vertex in 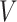 . The computational cost
of the algorithm is similar to that for computing a single Fréchet mean using the Sturm
algorithm. For
. The computational cost
of the algorithm is similar to that for computing a single Fréchet mean using the Sturm
algorithm. For 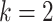 the initial point
the initial point
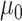 is sampled uniformly from the
perimeter of
is sampled uniformly from the
perimeter of 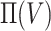 . Convergence is tested as follows:
at iteration
. Convergence is tested as follows:
at iteration 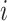 it is determined whether
it is determined whether
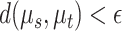 for all
for all
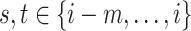 , where
, where
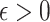 and
and 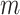 are
fixed; if that is the case, then the algorithm terminates. The output from the algorithm
after
are
fixed; if that is the case, then the algorithm terminates. The output from the algorithm
after 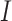 iterations is an estimate
iterations is an estimate
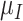 of the projection of
of the projection of
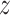 and a vector
and a vector 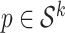 .
.
The geometric projection algorithm is presented here without a proof of convergence and without further theoretical study of its properties. Instead we rely on a simulation study in the next subsection to assess its effectiveness.
4.2. Simulations
We ran simulations designed to demonstrate that, specifically in the case of
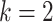 , Algorithm 3 converges to a tree on
, Algorithm 3 converges to a tree on
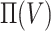 which minimizes
which minimizes
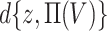 . For each iteration of the
simulation, a random species tree
. For each iteration of the
simulation, a random species tree 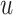 with
with
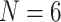 taxa was generated under the Kingman (1982) coalescent. Three trees
taxa was generated under the Kingman (1982) coalescent. Three trees
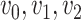 and a fourth test tree
and a fourth test tree
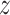 were then generated under a coalescent
model constrained to be contained within the tree
were then generated under a coalescent
model constrained to be contained within the tree 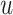 , and
thus corresponded to gene trees coming from the underlying species tree
, and
thus corresponded to gene trees coming from the underlying species tree
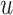 . Maddison
(1997) describes in detail the relationship between species trees and gene trees.
The DendroPy library (Sukumaran & Holder, 2010)
was used to generate these trees. The test tree
. Maddison
(1997) describes in detail the relationship between species trees and gene trees.
The DendroPy library (Sukumaran & Holder, 2010)
was used to generate these trees. The test tree  was then projected onto
was then projected onto
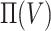 for
for 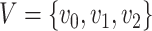 using the exhaustive search
algorithm and the geometric projection algorithm. All calculations were carried out
ignoring pendant edges. This particular simulation scheme was chosen in order to generate
a variety of different geometrical configurations for the points
using the exhaustive search
algorithm and the geometric projection algorithm. All calculations were carried out
ignoring pendant edges. This particular simulation scheme was chosen in order to generate
a variety of different geometrical configurations for the points 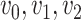 and
and  , as
well as being biologically reasonable. If the trees were sampled with topologies chosen
independently uniformly at random, for example, the simulation procedure would only have
explored instances of
, as
well as being biologically reasonable. If the trees were sampled with topologies chosen
independently uniformly at random, for example, the simulation procedure would only have
explored instances of 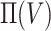 with widely differing vertices.
with widely differing vertices.
The results obtained from the two algorithms were compared in two ways. First, the distances from the data tree to the projected trees obtained with the two algorithms were computed and checked to ensure that the projection algorithm yielded a distance less than or equal to the exhaustive search. Second, the distance between the tree from geometric projection and the tree from exhaustive search was checked to ensure that the two trees were close together. For the second check we considered any distance greater than 1% of the total internal length of the data tree to be a failure.
In a run of 10 000 replications of this procedure, 95 7%
of the replications passed the two tests. However, even the set of failing replications
produced a projection result that was quite close to the exhaustive search result. Among
the 435 failing replications, the perpendicular distance for the projection was an average
of 3
7%
of the replications passed the two tests. However, even the set of failing replications
produced a projection result that was quite close to the exhaustive search result. Among
the 435 failing replications, the perpendicular distance for the projection was an average
of 3 7% greater than the perpendicular
distance of the exhaustive search, and the distance between the two results was an average
of 4
7% greater than the perpendicular
distance of the exhaustive search, and the distance between the two results was an average
of 4 7% of the total internal length of the
data tree.
7% of the total internal length of the
data tree.
We believe that the failing results are attributable to the projection algorithm becoming trapped in local minima of the perpendicular distance. Starting the algorithm from several locations and comparing the results would help to mitigate this problem. However, for the present purpose of fitting higher principal components to a collection of data trees, we believe these small deviations from the exhaustive search solution are an acceptable trade for the increase in computational speed.
4.3. Stochastic optimization for principal component analysis
Given data 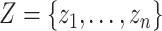 , our objective is to
find
, our objective is to
find 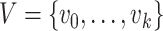 that minimizes the sum
of squared projected distances
that minimizes the sum
of squared projected distances 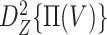 . We
henceforth restrict ourselves to the case
. We
henceforth restrict ourselves to the case 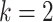 . The geometric
projection algorithm is used to compute
. The geometric
projection algorithm is used to compute 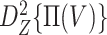 given
given
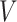 , at least approximately, so we must now
consider how to search over the possible configurations of the vertices
, at least approximately, so we must now
consider how to search over the possible configurations of the vertices
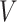 . We adopt a stochastic optimization
approach, Algorithm 4 below, which is similar to that used for fitting principal geodesics
in Nye (2014). We assume that we have available a
set of proposals
. We adopt a stochastic optimization
approach, Algorithm 4 below, which is similar to that used for fitting principal geodesics
in Nye (2014). We assume that we have available a
set of proposals 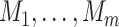 , each of which is a map from
, each of which is a map from
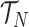 to the set of distributions
on
to the set of distributions
on 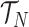 . In particular, given any
tree
. In particular, given any
tree 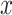 , each
, each 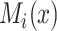 is assumed to be a distribution on
is assumed to be a distribution on 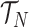 from
which we can easily sample.
from
which we can easily sample.
Algorithm 4.
Stochastic optimization algorithm to fit
to
.
Fix an initial set
and compute
.
Repeat:
For
:
For
:
Sample a tree
from
.
Let
be the set
but with
replacing
.
Compute
using the geometric projection algorithm.
If
set
.
Until convergence.
The optimization algorithm attempts to minimize 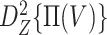 by stochastically varying one
point
by stochastically varying one
point 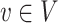 at a time using the proposals
at a time using the proposals
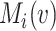 . The algorithm is greedy: whenever a
configuration
. The algorithm is greedy: whenever a
configuration 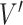 improves upon the current configuration
improves upon the current configuration
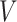 we replace
we replace 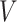 with
with
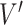 . Convergence is assessed by considering
the relative change in
. Convergence is assessed by considering
the relative change in 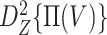 over a certain fixed number
of iterations. If this is less than some proportion then the algorithm terminates. We used
three different types of proposal. The first samples a tree uniformly at random with
replacement from the dataset
over a certain fixed number
of iterations. If this is less than some proportion then the algorithm terminates. We used
three different types of proposal. The first samples a tree uniformly at random with
replacement from the dataset  . The second type is a refinement of the
first: given a tree
. The second type is a refinement of the
first: given a tree  it similarly samples a tree
it similarly samples a tree
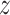 uniformly at random with replacement from
the dataset
uniformly at random with replacement from
the dataset 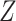 ; then the geodesic
; then the geodesic
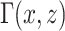 is computed, and a beta
distribution is used to sample a tree some proportion of the distance along
is computed, and a beta
distribution is used to sample a tree some proportion of the distance along
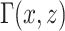 . The third type of proposal is
a random walk starting from
. The third type of proposal is
a random walk starting from 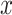 , as described in Nye (2014). The random walk proposals can have different numbers of
steps and step sizes. The algorithm is not guaranteed to find a global optimum, and it can
become stuck in local minima, so the algorithm must be run with different starting points
for each dataset, and then compare the results from each run.
, as described in Nye (2014). The random walk proposals can have different numbers of
steps and step sizes. The algorithm is not guaranteed to find a global optimum, and it can
become stuck in local minima, so the algorithm must be run with different starting points
for each dataset, and then compare the results from each run.
Two statistics can be used to summarize the fit of 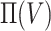 to a dataset
to a dataset 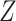 : the sum of squared projected distances
: the sum of squared projected distances
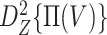 and a non-Euclidean
proportion of variance statistic, denoted by
and a non-Euclidean
proportion of variance statistic, denoted by 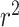 . If the projection of
each data point
. If the projection of
each data point 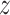 onto
onto 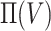 is denoted by
is denoted by 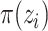 and
and  denotes the Fréchet mean of
denotes the Fréchet mean of
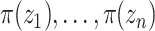 , then
, then
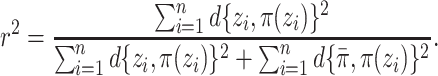 |
The denominator in this expression varies with  since Pythagoras’
theorem does not hold in tree space. Unlike
since Pythagoras’
theorem does not hold in tree space. Unlike 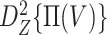 , the
, the
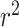 statistic is quite sensitive to small
changes in
statistic is quite sensitive to small
changes in 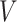 , but it can be interpreted broadly as the
proportion of variance explained by
, but it can be interpreted broadly as the
proportion of variance explained by 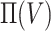 .
.
To assess the performance of the algorithm we conducted a small simulation study. Eight
datasets of 100 trees containing 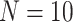 taxa were generated
in the following way. For each dataset a tree topology was sampled from a coalescent
process, and each edge length was sampled from a gamma distribution with shape
taxa were generated
in the following way. For each dataset a tree topology was sampled from a coalescent
process, and each edge length was sampled from a gamma distribution with shape
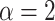 and rate
and rate 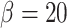 , to give a tree
, to give a tree
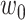 . Two trees
. Two trees 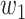 and
and
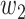 were then obtained by applying random
topological operations to
were then obtained by applying random
topological operations to 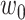 . In four of the datasets,
. In four of the datasets,
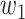 and
and 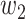 were
obtained by performing nearest-neighbour interchange operations, while in the other four
datasets subtree prune and regraft operations were used. Then, to construct each dataset
given
were
obtained by performing nearest-neighbour interchange operations, while in the other four
datasets subtree prune and regraft operations were used. Then, to construct each dataset
given 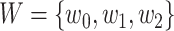 , 100 points were sampled
from a Dirichlet distribution on
, 100 points were sampled
from a Dirichlet distribution on 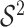 with
parameter
with
parameter 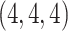 , and the corresponding points on
, and the corresponding points on
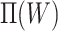 were found using the Bačák
algorithm. Each point was then perturbed by using a random walk, so that each dataset
resembled a cloud of points around the surface
were found using the Bačák
algorithm. Each point was then perturbed by using a random walk, so that each dataset
resembled a cloud of points around the surface  . The step size of
the random walk was tuned to produce datasets classified as having either low or high
dispersion. Table 1 summarizes the datasets used
and the simulation results. The stochastic optimization algorithm performs well in every
scenario.
. The step size of
the random walk was tuned to produce datasets classified as having either low or high
dispersion. Table 1 summarizes the datasets used
and the simulation results. The stochastic optimization algorithm performs well in every
scenario.
Table 1.
Simulations to assess the stochastic optimization algorithm: the leftmost
column describes the number and type of topological operation used to obtain
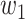 and
and 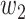 from
from 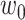 for each dataset; in each
scenario, two datasets were generated by perturbing points on
for each dataset; in each
scenario, two datasets were generated by perturbing points on
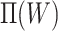 via random walks, with low
and high dispersions. Shown are the fitted values
via random walks, with low
and high dispersions. Shown are the fitted values 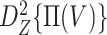 computed with the
geometric projection algorithm, with reference values
computed with the
geometric projection algorithm, with reference values 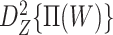 in parentheses,
computed with the exhaustive projection algorithm, together with the non-Euclidean
in parentheses,
computed with the exhaustive projection algorithm, together with the non-Euclidean
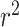 statistic, with reference
values in parentheses
statistic, with reference
values in parentheses
| Low dispersion | High dispersion | |||
|---|---|---|---|---|
| Topological scenario |
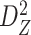
|
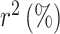
|
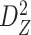
|
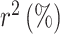
|
 nearest-neighbour interchange
nearest-neighbour interchange |
|
|
|
|
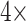 nearest-neighbour interchange
nearest-neighbour interchange |
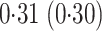
|
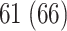
|
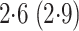
|
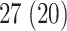
|
 subtree prune and regraft
subtree prune and regraft |
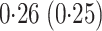
|
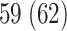
|
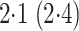
|
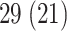
|
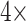 subtree prune and regraft
subtree prune and regraft |
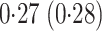
|
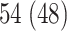
|
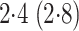
|
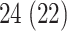
|
5. Results
5.1. Coelacanths genome and transcriptome data
We applied our method to the dataset comprising 1290 nuclear genes encoding 690 838 amino acid residues obtained from genome and transcriptome data by Liang et al. (2013). Over the past few decades researchers have worked on the phylogenetic relations between coelacanths, lungfishes and tetrapods, but controversy remains despite several studies (Hedges, 2009). Most morphological and palaeontological studies support the hypothesis that lungfishes are closer to tetrapods than they are to coelacanths. However, some research supports alternative hypotheses: that coelacanths are closer to tetrapods; that coelacanths and lungfish are closest; or that tetrapods, lungfishes and coelacanths cannot be resolved. Liang et al. (2013) present these four hypotheses in their Fig. 1, Trees 1–4, respectively.
We reconstructed gene trees using the R (R Development Core Team, 2017) package Phangorn (Schliep, 2011), with each gene tree estimated using maximum likelihood under the Le & Gascuel (2008) model. The dataset consisted of 1290 gene alignments for 10 species: lungfish, Protopterus annectens, and coelacanth, Latimeria chalumnae; three tetrapods, frog, Xenopus tropicalis, chicken, Gallus gallus, and human, Homo sapiens; two ray-finned fish, Danio rerio and Takifugu rubripes; and three cartilaginous fish included as an out-group, Scyliorhinus canicula, Leucoraja erinacea and Callorhinchus milii.
Analysis was performed ignoring pendant edge lengths. A total of 97 outlying trees were
removed using KDETrees (Weyenberg et al., 2016), so
that 1193 gene trees remained. The Fréchet mean was computed using the Bačák algorithm and
its topology is shown in Fig. 4. The mean tree does
not resolve whether coelacanth or lungfish is the closest relative of the tetrapods. The
sum of squared distances of the data points to the Fréchet mean was
19 7. A principal geodesic was
constructed using the algorithm from Nye (2014):
the sum of squared projected distances was 9
7. A principal geodesic was
constructed using the algorithm from Nye (2014):
the sum of squared projected distances was 9 53 and the
non-Euclidean
53 and the
non-Euclidean 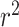 statistic was
51
statistic was
51 4%. Traversing the principal geodesic
gives trees with the same topology as the Fréchet mean that contract down to a star tree
at one end of the geodesic and expand in size at the other end. This shows that the
principal source of variation in the dataset is the overall scale of the gene trees or, in
other words, the total amount of evolutionary divergence for each gene.
4%. Traversing the principal geodesic
gives trees with the same topology as the Fréchet mean that contract down to a star tree
at one end of the geodesic and expand in size at the other end. This shows that the
principal source of variation in the dataset is the overall scale of the gene trees or, in
other words, the total amount of evolutionary divergence for each gene.
Fig. 4.
The second principal component computed from the lungfish dataset: (a) the simplex
shaded according to the topology of the corresponding points on
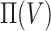 , with the projections of the
data points also displayed; (b) topologies of trees on
, with the projections of the
data points also displayed; (b) topologies of trees on 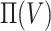 . Species abbreviations are based
on the binary nomenclature: lungfish, Pa; coelacanth,
Lc; frog Xt; chicken, Gg; human,
Hs; ray-finned fish, Dr and Tr;
cartilaginous fish, Sc, Le and Cm.
The number of data points projecting to each topology is displayed in brackets.
. Species abbreviations are based
on the binary nomenclature: lungfish, Pa; coelacanth,
Lc; frog Xt; chicken, Gg; human,
Hs; ray-finned fish, Dr and Tr;
cartilaginous fish, Sc, Le and Cm.
The number of data points projecting to each topology is displayed in brackets.
Figure 4 illustrates the second principal component.
The sum of squared projected distances was 7 29 and the
non-Euclidean
29 and the
non-Euclidean  statistic was
61
statistic was
61 8%. This represents a relatively small
increase in the proportion of variance in relation to the principal geodesic. Three runs
of Algorithm 4 were performed to construct the second principal component. The results
obtained had very similar summary statistics, but the topologies displayed on the surfaces
were more variable, so Fig. 4 is a representative
choice. Although the projected points are clustered towards the bottom of the simplex in
the figure, the full simplex was drawn to show all the different topological regions. Of
the 1193 gene trees, 1094 projected to points with topology 1, which supports lungfish
being the closest relative of the tetrapods. From the remaining projected data points, 75
have topology 5, placing both lungfish and coelacanth in a clade with the tetrapods. The
topologies 3, 4, 6 and 7 have biologically implausible relationships. However, the
projected data points lying outside topology 1 all lie close to the boundary of their
respective orthants, having at least one edge length less than 0
8%. This represents a relatively small
increase in the proportion of variance in relation to the principal geodesic. Three runs
of Algorithm 4 were performed to construct the second principal component. The results
obtained had very similar summary statistics, but the topologies displayed on the surfaces
were more variable, so Fig. 4 is a representative
choice. Although the projected points are clustered towards the bottom of the simplex in
the figure, the full simplex was drawn to show all the different topological regions. Of
the 1193 gene trees, 1094 projected to points with topology 1, which supports lungfish
being the closest relative of the tetrapods. From the remaining projected data points, 75
have topology 5, placing both lungfish and coelacanth in a clade with the tetrapods. The
topologies 3, 4, 6 and 7 have biologically implausible relationships. However, the
projected data points lying outside topology 1 all lie close to the boundary of their
respective orthants, having at least one edge length less than 0 0005. For example, the projected data
points with topology 3 have very short edge lengths for the biologically implausible
clades, such as the grouping of X. tropicalis with S.
canicula, and so lie close to trees with more plausible topologies.
0005. For example, the projected data
points with topology 3 have very short edge lengths for the biologically implausible
clades, such as the grouping of X. tropicalis with S.
canicula, and so lie close to trees with more plausible topologies.
Overall, the second principal component suggests that the data support topology 1, with
lungfish as the closest relative of tetrapods, and that most of the variation within the
data comes from edge length variation within that topology rather than from conflicting
topologies. Although the estimates are subject to random variation, it is interesting that
the Fréchet mean and principal geodesic did not exhibit topology 1, while the second
principal component suggests a solution to the controversial relationship between
coelacanth, lungfish and tetrapods. The exhaustive projection algorithm was used to
project the data onto the surface  produced by
Algorithm 4, in order to compare with the results obtained by geometric projection. The
sum of squared distances between the projected trees obtained with the two different
algorithms was 0
produced by
Algorithm 4, in order to compare with the results obtained by geometric projection. The
sum of squared distances between the projected trees obtained with the two different
algorithms was 0 004, a small fraction of the sum of
squared projected distances 7
004, a small fraction of the sum of
squared projected distances 7 29 for
29 for 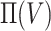 .
.
5.2. Apicomplexa
We also applied our method to a set of trees constructed from 268 orthologous sequences from eight species of protozoa in the Apicomplexa phylum, previously presented by Kuo et al. (2008). The same dataset was also analysed by Weyenberg et al. (2016), and more details are given in that paper, such as the gene sequences used to infer each tree. The phylum Apicomplexa contains many important protozoan pathogens (Levine, 1988), including the mosquito-transmitted Plasmodium species, the causative agent of malaria; T. gondii, which is one of the most prevalent zoonotic pathogens worldwide; and the water-borne pathogen Cryptosporidium species. Several members of the Apicomplexa also cause significant morbidity and mortality in both wildlife and domestic animals. These include the Theileria and Babesia species, which are tick-borne haemoprotozoan ungulate pathogens, and several species of Eimeria, which are enteric parasites that are particularly detrimental to the poultry industry. Because of their medical and veterinary importance, whole-genome sequencing projects have been completed for multiple prominent members of the Apicomplexa. We removed 16 outlier trees previously identified by Weyenberg et al. (2016) before fitting principal components.
The trees were analysed ignoring pendant edges. The Fréchet mean was computed using the
Bačák algorithm: the corresponding tree topology was unresolved, and is shown in Fig. 5. The sum of squared distances from the mean to the
data points was 24 6. The principal geodesic was
estimated using the algorithm from Nye (2014). The
principal geodesic has a non-Euclidean
6. The principal geodesic was
estimated using the algorithm from Nye (2014). The
principal geodesic has a non-Euclidean 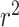 statistic of 40%, and
the sum of squared projected distances was 14
statistic of 40%, and
the sum of squared projected distances was 14 2. The principal
geodesic displays two main effects. First, the edges leading to the P.
vivax and P. falciparum clade, the E. tenella
and T. gondii clade, and the B. bovis and T.
annulata clade vary substantially in length. The second is a topological
rearrangement whereby the clade containing P. vivax and P.
falciparum paired with E. tenella and T.
gondii is replaced with a clade containing P. vivax and
P. falciparum paired with B. bovis and T.
annulata. However, the second effect involved very short internal edges, so
that along its length, the trees on the principal geodesic resembled the mean tree shown
in Fig. 5 but with different overall scale. The
principal geodesic therefore reflects variation in the scale of the tree.
2. The principal
geodesic displays two main effects. First, the edges leading to the P.
vivax and P. falciparum clade, the E. tenella
and T. gondii clade, and the B. bovis and T.
annulata clade vary substantially in length. The second is a topological
rearrangement whereby the clade containing P. vivax and P.
falciparum paired with E. tenella and T.
gondii is replaced with a clade containing P. vivax and
P. falciparum paired with B. bovis and T.
annulata. However, the second effect involved very short internal edges, so
that along its length, the trees on the principal geodesic resembled the mean tree shown
in Fig. 5 but with different overall scale. The
principal geodesic therefore reflects variation in the scale of the tree.
Fig. 5.
The second principal component computed from the Apicomplexa dataset: (a) the simplex
shaded according to the topology of the corresponding points on
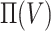 , with the projections of the
data points also displayed; (b) topologies of trees on
, with the projections of the
data points also displayed; (b) topologies of trees on 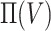 . Species abbreviations are based
on the species’ binary nomenclature. The number of data points projecting to each
topology is displayed in brackets.
. Species abbreviations are based
on the species’ binary nomenclature. The number of data points projecting to each
topology is displayed in brackets.
Figure 5 illustrates the second principal component,
with the simplex shaded according to the corresponding tree topology on
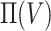 . Three separate runs of Algorithm 4
converged to give similar results. The summary statistics for the second principal
component are: sum of squared projected distances 10
. Three separate runs of Algorithm 4
converged to give similar results. The summary statistics for the second principal
component are: sum of squared projected distances 10 3;
non-Euclidean
3;
non-Euclidean 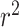 statistic 56%. While these summary
statistics were consistent between runs, the set of topologies displayed on
statistic 56%. While these summary
statistics were consistent between runs, the set of topologies displayed on
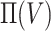 was subject to more variation, so
Fig. 5 is a representative choice, although
topologies 1, 4 and 6 were present in all runs. The results show how the second principal
component is able to tease out more from the data than the variation in overall scale
captured by the principal geodesic. Topology 4 is congruent with the generally accepted
phylogeny of taxa within the Apicomplexa and is a resolution of the Fréchet mean tree:
T. annulata and B. bovis group together; the two
Plasmodium species group together; C. parvum is the
deepest rooting apicomplexan; and P. vivax, P.
falciparum, T. annulata and B. bovis are
monophyletic. The latter group are all haemosporidians or blood parasites.
was subject to more variation, so
Fig. 5 is a representative choice, although
topologies 1, 4 and 6 were present in all runs. The results show how the second principal
component is able to tease out more from the data than the variation in overall scale
captured by the principal geodesic. Topology 4 is congruent with the generally accepted
phylogeny of taxa within the Apicomplexa and is a resolution of the Fréchet mean tree:
T. annulata and B. bovis group together; the two
Plasmodium species group together; C. parvum is the
deepest rooting apicomplexan; and P. vivax, P.
falciparum, T. annulata and B. bovis are
monophyletic. The latter group are all haemosporidians or blood parasites.
Figure 5 shows that the second principal component
corresponds to variation in topology consisting of nearest-neighbour interchange
operations that transform topology 4 into topologies 1 and 6. None of the projected trees
have topology 5, although this is the topology of one of the vertices of
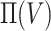 . This topology appears to be present
in order for
. This topology appears to be present
in order for 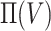 to be positioned in such a way as to
capture the other topologies. Topology 2 shows evidence of stickiness, as discussed in §
3.1. Although the topology is unresolved, so
that the coloured triangle lies in a codimension-
to be positioned in such a way as to
capture the other topologies. Topology 2 shows evidence of stickiness, as discussed in §
3.1. Although the topology is unresolved, so
that the coloured triangle lies in a codimension- region
of tree space, it occupies the nonzero area on the simplex. As for the lungfish, the
exhaustive and geometric projection algorithms were compared on the surface
region
of tree space, it occupies the nonzero area on the simplex. As for the lungfish, the
exhaustive and geometric projection algorithms were compared on the surface
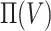 produced by Algorithm 4. The
distances between the projected points obtained with the two algorithms were very small
compared to the distances of the data points from
produced by Algorithm 4. The
distances between the projected points obtained with the two algorithms were very small
compared to the distances of the data points from  :
the sum of squared distances between pairs of projected points was
:
the sum of squared distances between pairs of projected points was
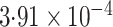 .
.
6. Discussion
This paper presents three main innovations: (i) use of the locus of the Fréchet mean
 as an analogue of a principal
component in tree space; (ii) proof that
as an analogue of a principal
component in tree space; (ii) proof that  has the desired
dimension; and (iii) the geometric projection algorithm for projecting data onto
has the desired
dimension; and (iii) the geometric projection algorithm for projecting data onto
 . The locus of the Fréchet mean was
first proposed as a geometric object for principal component analysis in tree space in a
2015 University of Kentucky PhD thesis by G. Weyenberg. Pennec (2015) made a similar proposal for an analogue of principal component
analysis in Riemannian manifolds and other geodesic metric spaces, called barycentric
subspace analysis. The barycentric subspaces of Pennec correspond exactly to the surfaces
. The locus of the Fréchet mean was
first proposed as a geometric object for principal component analysis in tree space in a
2015 University of Kentucky PhD thesis by G. Weyenberg. Pennec (2015) made a similar proposal for an analogue of principal component
analysis in Riemannian manifolds and other geodesic metric spaces, called barycentric
subspace analysis. The barycentric subspaces of Pennec correspond exactly to the surfaces
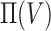 considered in this paper, except that
the weights
considered in this paper, except that
the weights 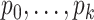 are not constrained to lie in
the simplex and can be negative. Pennec’s approach, however, is principally based in the
context of a Riemannian manifold rather than in tree space, though he points out the
potential for generalization. There are substantial differences between barycentric subspace
analysis and the method presented in this paper. In particular, a key aim of barycentric
subspace analysis is to produce nested principal components,
are not constrained to lie in
the simplex and can be negative. Pennec’s approach, however, is principally based in the
context of a Riemannian manifold rather than in tree space, though he points out the
potential for generalization. There are substantial differences between barycentric subspace
analysis and the method presented in this paper. In particular, a key aim of barycentric
subspace analysis is to produce nested principal components, 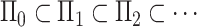 ,
while we do not have that restriction here. The nesting is achieved by either adding or
removing points from
,
while we do not have that restriction here. The nesting is achieved by either adding or
removing points from 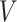 in order to obtain, respectively, a higher-
or lower-order nested principal component. This is also possible in the context of our
analysis, but the
in order to obtain, respectively, a higher-
or lower-order nested principal component. This is also possible in the context of our
analysis, but the 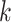 th principal component would in each case
form part of the boundary of the
th principal component would in each case
form part of the boundary of the 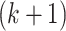 th principal
component. This is undesirable as it leads to poorly fitting principal components. For
example, suppose that the second principal component is constructed by adding an extra
vertex to the principal geodesic; many data points would project onto the edge of the second
principal component corresponding to the principal geodesic rather than being distributed
over the interior of the surface. Similar problems arise if the analysis is performed by
removing points from
th principal
component. This is undesirable as it leads to poorly fitting principal components. For
example, suppose that the second principal component is constructed by adding an extra
vertex to the principal geodesic; many data points would project onto the edge of the second
principal component corresponding to the principal geodesic rather than being distributed
over the interior of the surface. Similar problems arise if the analysis is performed by
removing points from 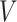 sequentially. These problems do not arise
with Pennec’s methodology, because the weights
sequentially. These problems do not arise
with Pennec’s methodology, because the weights 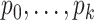 are not
restricted to the simplex, so a nested principal component can lie in the interior of
higher-order components. In contrast, the existing algorithms for computing the Fréchet mean
in tree space and our algorithm for projection onto
are not
restricted to the simplex, so a nested principal component can lie in the interior of
higher-order components. In contrast, the existing algorithms for computing the Fréchet mean
in tree space and our algorithm for projection onto 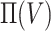 all
require the weights
all
require the weights 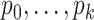 to lie in the simplex, and
this motivated the decision to consider principal components which are not nested in this
paper. If these algorithms could be adapted to allow negative values for the weights, then a
nested principal component analysis would be possible in tree space.
to lie in the simplex, and
this motivated the decision to consider principal components which are not nested in this
paper. If these algorithms could be adapted to allow negative values for the weights, then a
nested principal component analysis would be possible in tree space.
Our analysis has been restricted to datasets with relatively few taxa and to the
construction of the first and second principal components. The algorithms presented in this
paper scale linearly with respect to the number of data points 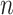 , but run
in polynomial time with respect to the number of taxa
, but run
in polynomial time with respect to the number of taxa 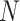 .
However, by partitioning the dataset for the geometric projection algorithm, parallel
computer architectures can be employed and the speed-up is approximately proportional to the
number of processors used. While the geometric projection algorithm runs relatively quickly,
the calculations involved in searching for the optimal set of vertices
.
However, by partitioning the dataset for the geometric projection algorithm, parallel
computer architectures can be employed and the speed-up is approximately proportional to the
number of processors used. While the geometric projection algorithm runs relatively quickly,
the calculations involved in searching for the optimal set of vertices
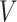 can be very substantial. The experimental
datasets in § 5 took between one and three days to
analyse, running on four processors each. For higher-order components,
can be very substantial. The experimental
datasets in § 5 took between one and three days to
analyse, running on four processors each. For higher-order components,
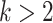 , this computational burden will increase,
and it is likely that finding a global minimum for
, this computational burden will increase,
and it is likely that finding a global minimum for 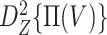 will be more difficult. While
the method presented in this paper generalizes to arbitrary
will be more difficult. While
the method presented in this paper generalizes to arbitrary 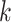 ,
including the geometric projection algorithm, computational issues limited our analysis to
,
including the geometric projection algorithm, computational issues limited our analysis to
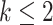 . However, fitting a principal
component
. However, fitting a principal
component 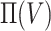 with
with 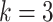 would
give an upper bound on
would
give an upper bound on 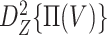 even if a global minimum were
not found, and hence an approximate lower bound on the non-Euclidean
even if a global minimum were
not found, and hence an approximate lower bound on the non-Euclidean
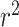 statistic. Consequently, even a poorly
fit principal component with
statistic. Consequently, even a poorly
fit principal component with 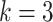 might give some indication of the
additional variance explained by higher-order components.
might give some indication of the
additional variance explained by higher-order components.
Uncertainty in estimated principal components could be assessed by bootstrap methods; for
example, one can generate replicate datasets by resampling the data
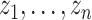 and constructing principal
components for each replicate. An alternative bootstrap procedure involves estimating a
principal component
and constructing principal
components for each replicate. An alternative bootstrap procedure involves estimating a
principal component 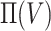 for
for 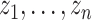 and then generating replicate
datasets by randomly perturbing the projection of each point
and then generating replicate
datasets by randomly perturbing the projection of each point 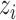 onto
onto
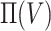 using a random walk, in a similar way
to the simulations in § 4.3. However, both these
approaches are highly computationally expensive, and would only be feasible for relatively
small datasets. Obtaining analytical results about uncertainty, such as proving validity of
the bootstrap procedure or establishing confidence regions for principal components, would
involve development of asymptotic theory on the space of configurations of the vertices
using a random walk, in a similar way
to the simulations in § 4.3. However, both these
approaches are highly computationally expensive, and would only be feasible for relatively
small datasets. Obtaining analytical results about uncertainty, such as proving validity of
the bootstrap procedure or establishing confidence regions for principal components, would
involve development of asymptotic theory on the space of configurations of the vertices
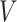 , and this lies well beyond existing
probability theory on tree space (Barden et al.,
2013).
, and this lies well beyond existing
probability theory on tree space (Barden et al.,
2013).
The figures in § 5 demonstrate the potential for creating visualizations of the data which reveal meaningful biological structure. The pattern of projected points obtained for the experimental datasets we considered were very similar to results obtained via multi-dimensional scaling. However, multi-dimensional scaling is not capable of revealing the features of the dataset that cause the observed variation. More information could be included in the graphical representation of our results, such as the distance of the data points from their projections, information about the principal geodesic, and the proximity of points to orthant boundaries.
Our software for finding principal components in tree space is available to download from http://www.mas.ncl.ac.uk/~ntmwn/geophytterplus/. The datasets analysed in this paper are also available from that website. An optional R package used to produce the figures in this article can be obtained from https://github.com/grady/geophyttertools.
We presented Algorithm 3, the geometric projection algorithm, without a proof of convergence, and we used simulation to assess its accuracy. The algorithm is attractive in that it is defined entirely in terms of the geodesic structure on tree space, so it could be used on any geodesic metric space, including Riemannian manifolds. The algorithm clearly deserves further investigation, and we intend to study its properties in future work.
Supplementary Material
Acknowledgement
The authors thank D. Howe from the University of Kentucky for useful comments on the analysis of the Apicomplexa dataset. Grady Weyenberg acknowledges support from the Wellcome Trust and the Medical Research Council Integrative Epidemiology Unit, University of Bristol, U.K. Xiaoxian Tang acknowledges support from the Zentrale Forschungsförderung of the University of Bremen, Germany.
Supplementary material
Supplementary material available at Biometrika online includes the proof of Lemma 2 and the geophytter+ software, which implements the algorithms described in this paper.
References
- Barden D., Le H. & Owen M. (2013). Central limit theorems for Fréchet means in the space of phylogenetic trees. Electron. J. Prob. 18, 1–25. [Google Scholar]
- Bačák M. (2014). Computing medians and means in Hadamard spaces. SIAM J. Optimiz. 24, 1542–66. [Google Scholar]
- Billera L. J., Holmes S. P. & Vogtman K. (2001). Geometry of the space of phylogenetic trees. Adv. Appl. Math 27, 733–67. [Google Scholar]
- Bridson M. R. & Haefliger A. (2011). Metric Spaces of Non-Positive Curvature. Berlin: Springer. [Google Scholar]
-
Ding C. & He X.
(2004).
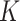 -means clustering via
principal component analysis. In Proc. 21st Int. Conf. Mach.
Learn. Banff: Association for
Computing Machinery, p. 29. [Google Scholar]
-means clustering via
principal component analysis. In Proc. 21st Int. Conf. Mach.
Learn. Banff: Association for
Computing Machinery, p. 29. [Google Scholar] - Feragen A., Owen M., Petersen J., Wille M. M. W., Thomsen L. H., Dirksen A. & de Bruijne M. (2013). Tree-space statistics and approximations for large-scale analysis of anatomical trees. In Information Processing in Medical Imaging (23rd Int. Conf. Proc.), Gee J. C.Joshi S.Pohl K. M.Wells W. M. & Zollei L. eds. Berlin: Springer. [DOI] [PubMed] [Google Scholar]
- Gori K., Suchan T., Alvarez N., Goldman N. & Dessimoz C. (2016). Clustering genes of common evolutionary history. Molec. Biol. Evol. 33, 1590–605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedges S. (2009). Vertebrates (Vertebrata). In The Timeline of Life, Hedges S. B. & Kumar S. eds. New York: Oxford University Press, pp. 309–14. [Google Scholar]
- Hillis D. M., Heath T. A. & St. John K. (2005). Analysis and visualization of tree space. Syst. Biol. 54, 471–82. [DOI] [PubMed] [Google Scholar]
- Hotz T., Huckemann S., Le H., Marron J. S., Mattingly J. C., Miller E., Nolen J., Owen M., Patrangenaru V. & Skwerer S. (2013). Sticky central limit theorems on open books. Ann. Appl. Prob. 23, 2238–58. [Google Scholar]
- Kingman J. F. C. (1982). The coalescent. Stoch. Proces. Appl. 13, 235–48. [Google Scholar]
- Kuo C., Wares J. P. & Kissinger J. C. (2008). The Apicomplexan whole-genome phylogeny: An analysis of incongruence among gene trees. Molec. Biol. Evol. 25, 2689–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le S. Q. & Gascuel O. (2008). An improved general amino acid replacement matrix. Molec. Biol. Evol. 25, 1307–20. [DOI] [PubMed] [Google Scholar]
- Levine N. D. (1988). Progress in taxonomy of the Apicomplexan protozoa. J. Eukaryot. Microbiol. 35, 518–20. [DOI] [PubMed] [Google Scholar]
- Liang D., Shen X. X. & Zhang P. (2013). One thousand two hundred ninety nuclear genes from a genome-wide survey support lungfishes as the sister group of tetrapods. Molec. Biol. Evol. 30, 1803–7. [DOI] [PubMed] [Google Scholar]
- Lin B., Sturmfels B., Tang X. & Yoshida R. (2016). Convexity in tree spaces. arXiv: 1510.08797v3. [Google Scholar]
- Lubiw A., Maftuleac D. & Owen M. (2017). Shortest paths and convex hulls in 2D complexes with non-positive curvature. arXiv: 1603.00847v4. [Google Scholar]
- Maddison W. P. (1997). Gene trees in species trees. Syst. Biol. 46, 523–36. [Google Scholar]
- Miller E., Owen M. & Provan J. S. (2015). Polyhedral computational geometry for averaging metric phylogenetic trees. Adv. Appl. Math. 68, 51–91. [Google Scholar]
- Nye T. M. W. (2011). Principal components analysis in the space of phylogenetic trees. Ann. Statist. 39, 2716–39. [Google Scholar]
- Nye T. M. W. (2014). An algorithm for constructing principal geodesics in phylogenetic treespace. IEEE/ACM Trans. Comp. Biol. Bioinfo. 11, 304–15. [DOI] [PubMed] [Google Scholar]
- Owen M. & Provan J. S. (2011). A fast algorithm for computing geodesic distances in tree space. IEEE/ACM Trans. Comp. Biol. Bioinfo. 8, 2–13. [DOI] [PubMed] [Google Scholar]
- Pennec X. (2015). Barycentric subspaces and affine spans in manifolds. In Geometric Science of Information (2nd Int. Conf. Proc.), Nielsen F. & Barbaresco F. eds. Palaiseau, France: Springer. [Google Scholar]
- R Development Core Team (2017). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0. http://www.R-project.org. [Google Scholar]
- Schliep K. P. (2011). Phangorn: Phylogenetic analysis in R. Bioinformatics 27, 592–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Semple C. & Steel M. A. (2003). Phylogenetics. Oxford: Oxford University Press. [Google Scholar]
- Sturm K.-T. (2003). Probability measures on metric spaces of nonpositive curvature. In Heat Kernels and Analysis on Manifolds, Graphs, and Metric Spaces, Pascal A.Coulhon T. & Grigor’yan A. eds. Providence, Rhode Island: American Mathematical Society, pp. 357–90. [Google Scholar]
- Sukumaran J. & Holder M. T. (2010). Dendropy: A Python library for phylogenetic computing. Bioinformatics 26, 1569–71. [DOI] [PubMed] [Google Scholar]
- Weyenberg G., Huggins P. M., Schardl C. L., Howe D. K. & Yoshida R. (2014). KDEtrees: Non-parametric estimation of phylogenetic tree distributions. Bioinformatics 30, 2280–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weyenberg G., Yoshida R. & Howe D. (2016). Normalizing kernels in the Billera-Holmes-Vogtmann treespace. IEEE/ACM Trans. Comp. Biol. Bioinfo. 10.1109/TCBB.2016.2565475. [DOI] [PubMed] [Google Scholar]
-
Zha H., Ding C., Gu M.,
He X. & Simon H.
D. (2001).
Spectral relaxation for
 -means
clustering. Neural Info. Proces. 14,
1057–64. [Google Scholar]
-means
clustering. Neural Info. Proces. 14,
1057–64. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.