Fig. 7.

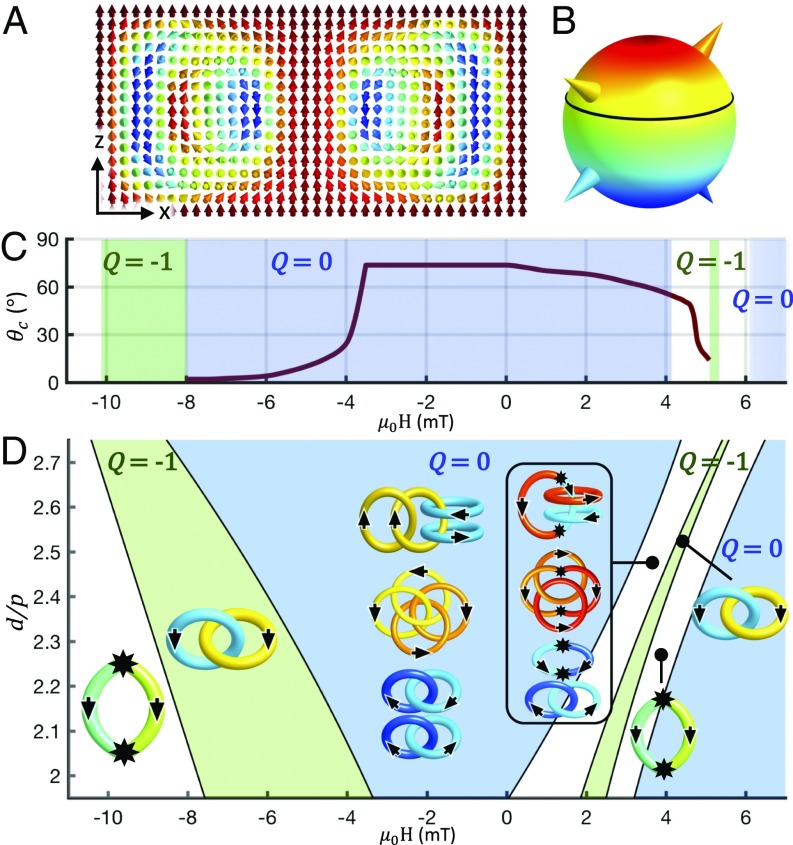
Stability of solitonic structures vs. d/p and H. (A) Computer-simulated cross-section of a stable axially symmetric Q = 0 soliton at H = 0 and d/p = 2.7. The cross-section is parallel to n₀ and passes through the soliton’s symmetry axis. For more details on preimages of this soliton, see Movie S4. (B) Ground-state manifold ${\mathbb{S}}^2$ with four points (depicted by colored cones) corresponding to preimages of the same color schematically shown in D, Insets. Black circle shows the boundary line at θ_c = 73.5° separating subspaces of ${\mathbb{S}}^2$ with different types of individual preimages [double unlinked loops ($0_1^2$) for θ > θ_c and a Hopf link of closed loops ($2_1^2$) for θ < θ_c]. (C) θ_c and Q vs. μ₀H at d/p = 2.7. Q values are indicated atop of the colored regions of constant Q = −1 (green regions) and Q = 0 (blue regions). Singular point defects accompany the nonsingular solitons, forming torons, within the white uncolored regions. The critical angle is almost unaltered when H is antiparallel to M₀ and while its strength increases up to μ₀H = −3.5 mT, at which θ_c starts to drop rapidly to zero. At μ₀H = −8 mT, a discontinuous transformation changes Q from 0 to −1. At fields H antiparallel to M₀ with μ₀H = −10.1 mT and stronger, the field configuration is singular and resembles the structure of an elementary toron (25). The critical angle θ_c drops gradually with increasing the field strength for H parallel to M₀, and self-compensating singular point defects emerge starting at μ₀H = 4.1 mT, yielding the axially symmetric field configuration of a toron with 3π twist from its central axis to the far field periphery, dubbed “3π toron” (4), with a critical polar angle on ${\mathbb{S}}^2$ across which preimages have different topologies (4). At μ₀H = 5.2 mT, a smooth field configuration is recovered, and an elementary hopfion of Q = −1 is stabilized. At larger μ₀H, the field becomes singular again, and elementary torons form (4, 25). The field configuration becomes monodomain uniform starting at 6.1 mT. μ₀H is defined as positive when H is parallel to M₀ and negative when antiparallel to it. (D) Stability diagram of the solitons vs. d/p and the magnetic field strength μ₀H. Insets depict the diverse topology of two-point preimages and their links for a family of hopfions with Q = 0, −1, and two different types of torons that are stabilized in different regions of the diagram. The black filled stars atop some of the linking diagrams indicate the locations of point singularities at which individual preimages can terminate. Computer simulations were performed for material parameters of the chiral ferromagnetic LC based on the nematic host ZLI-2806 doped with ferromagnetic nanoplates and for the cell geometry with M₀ fixed at both the confining substrates and on the cylindrical region of the far-field periphery of the soliton. The host material was formed by dispersing nanoplates, each with a magnetic moment of 1.2 × 10⁻¹⁷ A⋅m², in a chiral LC at number density of 10 μm⁻³.