A roadmap to computational social neuroscience

Abstract

To complement experimental efforts toward understanding human social interactions at both neural and behavioral levels, two computational approaches are presented: (1) a fully parameterizable mathematical model of a social partner, the Human Dynamic Clamp which, by virtue of experimentally controlled interactions between Virtual Partners and real people, allows for emergent behaviors to be studied; and (2) a multiscale neurocomputational model of social coordination that enables exploration of social self-organization at all levels—from neuronal patterns to people interacting with each other. These complementary frameworks and the cross product of their analysis aim at understanding the fundamental principles governing social behavior.

Introduction

In proposing a framework for Computational Social Neuroscience, we are guided by the broader enterprise of Computational Neuroscience, an essential line of research to understanding brain and behavior. The complementary approach, empirical science, affords only a partial view of the system’s spatiotemporal organization, observed dynamics being restricted to certain domains of phase space. The comprehensive organization of the system’s dynamics is concealed, as is the continuity between qualitatively distinct states (e.g. normal and pathological regimes; distinct behavioral or cognitive states). Dynamical modeling of the brain provides a simplified but more extensive view: it stretches the boundaries of empirical data, exposes continuity between qualitatively different regimes, shows the paths leading from one regime to another, and attempts to reveal the entire parameter space—with the ultimate goal of discovering fundamental laws governing brain and behavior (Freeman 2001; Kelso 1995).

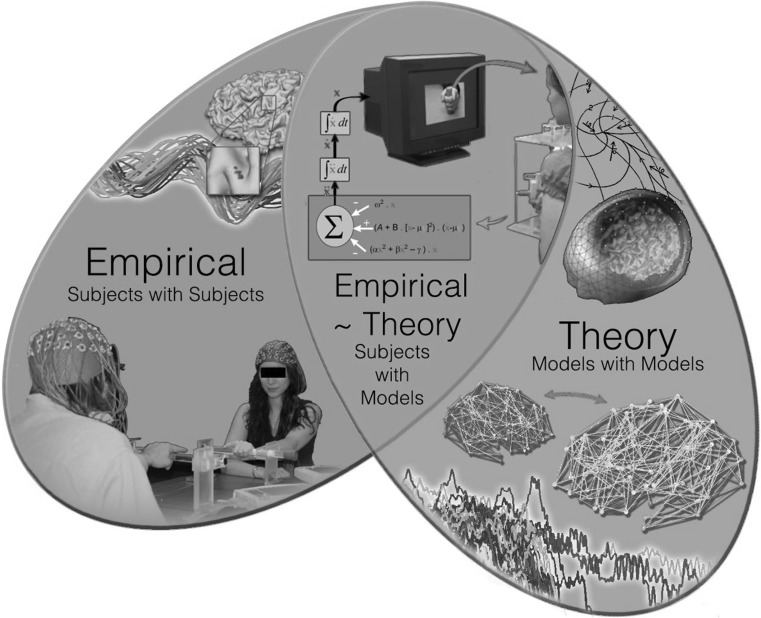
As a branch of neuroscience concerned with the coordination of behavior between individuals, social neuroscience is well positioned to benefit from computational approaches. In the following, we outline some unique opportunities that have arisen recently. After presenting the theoretical foundations, we review a hybrid framework in which human subjects, by virtue of mutual coupling, interact with mathematically-modeled partners in real-time (Kelso et al. 2014). This framework, called the Virtual Partner (Kelso et al. 2009) or Human Dynamic Clamp (HDC) (Dumas et al. 2014), leads to the study of brain and behavior in the human subject, controllable parameters in the virtual partner, and coordination dynamics of both (Fig. 1, center). Next, we discuss computational efforts (Fig. 1, right), in which two or more people are modeled, in order to shed light on the behavioral and neural underpinnings of social interactions. In a system perspective, social coordination can be described by trajectories of state variables drawn from several levels: neural (dynamics of neural ensembles measured by, e.g. EEG, MEG, fMRI), behavioral (dynamics of individual behavior) and social (dynamics of collective variables) (Kelso et al. 2013). In such multiscale modeling efforts, surrogate subjects are represented as mathematical models of self-sustained oscillations describing activity in neural areas and body parts that interact through (e.g. visual) perception of partners’ behavior. Finally, we discuss how to articulate meaningfully the efforts of experiments and models to gain a more comprehensive understanding of basic social interactions.

Fig. 1.

Complementarities between experimental and computational social neuroscience. Left panel shows some empirical studies of brain and behavior during coordination tasks; right panel illustrates modeling studies of brain and behavior (computational social models) and center panel shows the hybrid computational–experimental paradigm of the Human Dynamic Clamp, where real people are set to interact in real time with computational models of social partners

Theoretical framework and mathematical models

Coordination is a central tenet of Computational Social Neuroscience. While a large number of models of brain and behavior are formalized as individual dynamics (e.g., $x$) whose trajectories are determined by coupling to other variables ($\dot{x}=f\left(x,y\right)$, with $y$ a variable affecting $x$), a series of models are explicitly built on quantities that describe, not only the trajectories of parts, but also the trajectories of variables describing their coordination ($\dot{\mathit{\varphi }}=f\left(\mathit{\varphi }\right)$) with $\mathit{\varphi }$ is a variable describing coordination between, say, $x$ and $y$, thereby the name, Coordination Dynamics. The Haken–Kelso–Bunz (HKB) model (Haken et al. 1985) is a system of (nonlinearly) coupled nonlinear oscillators that reproduces essential properties of biological coordination (e.g. different forms of phase synchrony, instability, phase transitions, etc.) whose empirical study led to the further discovery of a host of complex phenomena such as critical slowing down, fluctuation enhancement, hysteresis, etc. (see Riley et al. 2011 for recent review). In HKB, symmetry plays a big role in restricting dynamical possibilities. A subsequently developed model of coordination, the extended version of HKB (Kelso et al. 1990) broke symmetry, thereby acknowledging that oscillators can have different intrinsic dynamics. With this extension, it became possible to handle coordination of dissimilar elements taken from a wide range of levels and scales, and at the same time, to achieve a greater realism, since in Nature, symmetry is constantly broken. Thus, heterogeneity—a difficulty faced in many computational efforts, especially in systems with large number of elements—was returned to scientific reach (Kelso and Tognoli 2007; Tognoli and Kelso 2014). The extended HKB model’s broken symmetry led to new insight into metastability which has been proposed as a fundamental principle of brain and behavior (Kelso 1995; Freeman 2001; Kelso and Tognoli 2007; Bressler and Kelso 2001; Freeman and Holmes 2005; Friston 1997; Kelso 2012; Fingelkurts and Fingelkurts 2004; Rabinovich et al. 2008; Tognoli and Kelso 2009, 2014; Werner 2007). A further step in the development of HKB was to create the mathematical conditions for discrete behaviors to arise from the continuous dynamics of the system’s self-sustained oscillators, the so-called ‘Excitator’ model (Jirsa and Kelso 2005). Although it seems intuitive that continuous behavior is the result of a juxtaposition of discrete actions, nature may go the other way around, using basic building blocks with self-sustained dynamics such as central pattern generators to produce discrete behaviors (Grillner 2011; Yuste et al. 2005). Further, adaptive coordination was developed by making previously fixed parameters of the coordination equations (e.g. intrinsic frequency) dynamic and time-dependent, giving rise to an augmented behavioral repertoire in the model (Kelso et al. 2009). Finally, directed coordination was developed to bias the collective behavior toward the “intention” of one of the oscillators, leading it to become a “teacher” to the other (Kelso et al. 2009), to the effect that HDC’s human partners could learn new patterns of collective behavior (Kostrubiec et al. 2015). Over the course of three decades, the overall framework of Coordination Dynamics has been built upon an ongoing program of research that blends theory, experimental observations, data analysis and modeling. The fact that its predictions have been confirmed at behavioral, neural and social levels (e.g. Kelso et al. 2009, 2013; Dumas et al. 2014; Tognoli et al. 2007, 2010; Tognoli 2008; Oullier et al. 2008 for social evidence) renders Coordination Dynamics a viable foundation for computational social neuroscience.

The Human Dynamic Clamp (HDC)

Those models of Coordination Dynamics from section “Theoretical framework and mathematical models” can be studied as is, but they can also be deployed in experiments. In the hybrid experimental-modeling paradigm of the Human Dynamic Clamp, a human and its mathematical mirror, a Virtual Partner, are reciprocally coupled via the empirically-verified HKB equations of coordination dynamics (Kelso et al. 2009; Dumas et al. 2014). Virtual Partners perceive the movement of human partners through sensors, and humans interact with Virtual Partners by viewing the output of the computational model in real-time as an animated image on a computer screen. Both the intrinsic dynamics of the Virtual Partner and its coupling to the human can be manipulated in real-time. Human and Virtual Partners are provided with coordination tasks to jointly accomplish and behavioral coordination is studied as in human–human experiments. Importantly, while affording comparison with real social contexts, HDC allows experimental manipulations that are not easily accessible when studying the interaction between humans. For instance, it is not straightforward to guarantee a consistent set of parameters sustained by one partner to observe its systematic effect on the other, so that parameter space screening is hardly ever achieved in classical experiments of social interaction. In turn, incomplete views on parameter space are not fully helpful to guide modeling, and hide experimentally infrequent but important examinations of the bifurcations between regimes. It is not easy either to effect a controlled change in some parameters (e.g., suddenly decrease coupling strength in a quantifiably precise manner, change intention, etc.), whereas it is very simple to flip a parameter from the model during model interactions with humans. HDC has already led to the discovery of novel coordination behaviors and behavioral transitions not seen before in standard paradigms, presumably because it allows broader expanses of parameter space to be explored and manipulated (Kelso et al. 2009). Starting from equations for Virtual Partners’ rhythmic motion of a single body part at a single frequency, and varying the model equations according to the successive models mentioned in section “Theoretical framework and mathematical models”, it was possible to put the Human Dynamic Clamp on a path to ever more complex social behaviors (Dumas et al. 2014). In the principled design of HDC, each new task context does not constitute an independent implementation of a single target behavior. Rather, HDC builds human behavior from its more primitive foundations with the explicit idea of developing multi-functionality as an emergent property. By constructing each new mathematical model as a generalization of a previous version, a more complete behavioral repertoire is possible foretelling, perhaps, a future when the Human Dynamic Clamp will be able to deal with any arbitrary human behavior.

Multilevel and multiscale modeling of social coordination

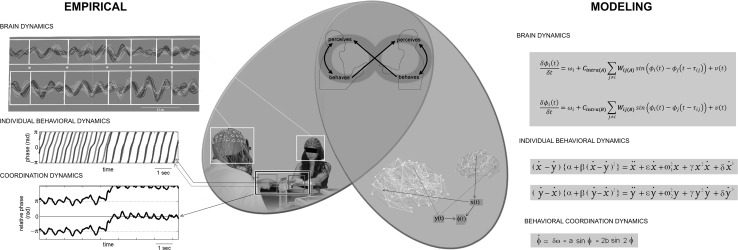
Integrating multiple levels of description into a single dynamical account is a longstanding feature of Coordination Dynamics (Kelso 1995; Kelso et al. 2013; Kelso and Tognoli 2007; Tognoli et al. 2010). Fully neurocomputational models of social behavior require at least three levels: the neural (brain dynamics), the behavioral (dynamics of body parts, e.g. hands or finger movement) and the social (dynamics of the behavioral coordination by people engaged in joint tasks). That is, there are systems of equations for two or more interacting people that describe what their brains are doing, what their body parts are doing, and how those body parts are coordinated (Fig. 2, right). Early work connected two levels, the behavioral and the social (Kelso et al. 2009; Dumas et al. 2014), while leaving the neural scale implicit (though the neural level is profoundly entwined in the mathematical description of social coordination behavior, it did not receive its own distinct equations). The neural level was explicitly integrated in Dumas et al. (2012) in a model that related the dynamics of social behavior with neural dynamics in a realistic architecture of brain areas (including interbrain structural symmetries). Realism was achieved by fingerprinting actual human brains: neural areas were obtained by anatomical brain atlas and connections from diffusion tensor imaging. Brain areas were mapped as neural masses to self-sustained oscillators coupled non-linearly with their phases. The coupling was neural within brain and informational between brains. Results assessed how the anatomical connectivity of the human brain enhances similarities of the neural dynamics and facilitates the creation of sensorimotor coupling between individuals (Dumas et al. 2012).

Fig. 2.

Neurocomputational Model of Social Interactions. Coupling between individuals is mediated by the behavior (center panel in mauve): observed motion of participant A entering B’s brain via perception (visual, auditory, haptic, etc.) and vice versa (i.e. we do not know of solid experimental evidence showing that brainwaves of one participant have a direct effect on another’s, sans mediation by behavioral exchange, but for the notable exception of purposefully engineered Brain-to-Brain Interfaces). Therefore, any model of the coupling between individuals has to be mediated by behavior. As a result, a theoretical model will have (e.g. two) brains, two or more behavioral effectors (e.g. moving fingers for a most elementary model, or vocal tracts, endocrine components, facial muscles, etc.) and in joint tasks with symmetry, a useful collective variable describing behavioral coordination. This order parameter at the behavioral level is deemed to function as a control parameter on brain dynamics. Left panel illustrates experimentally observed dynamics of brains (top), individual behaviors (middle) and behavioral coordination variable (bottom). Right panel illustrates some exemplary neurocomputational models of dyadic brain dynamics with, e.g. Kuramoto equations embedded in realistic connectomes (C_intra), scalable for coupling strength W_ij (top, after Dumas et al. 2012, see also, e.g. Jirsa and Kelso 2000; Fuchs et al. 2000 for other possible models), modeling of individual behavior (middle) and behavioral coordination variable (bottom), with (e.g. HKB) models of behavioral coordination. Such neurocomputational models of social behavior can be used in two ways: to clamp brain areas (e.g. set an oscillation at the sources of phi complex, a neuromarker of social coordination) and see effect on coordination behavior; or alternatively, to clamp coordination behavior (e.g. impose a pattern of behavioral coordination: metastable, stable locking inphase or antiphase, or some behavioral transitions) and observe how the brain reorganizes itself under those controlled circumstances. Furthermore, a similarly designed neurocomputational model can also be incorporated in the Human Dynamic Clamp (see Fig. 1 central panel) to test some hypotheses on the relationship between brain and behavior during live social interactions

Each of the three aforementioned levels might organize themselves at multiple spatiotemporal scales, for instance, spatially, the nervous system is known to organize at micro-, meso-, and macro-scales. A forthcoming step is to expand the spatial scales of the Dumas et al. (2012) model nervous system, with the addition of microscopic and mesoscopic levels as e.g., in Jirsa and Kelso (2000) and Deco et al. (2010). The social “Model-of-Models” will then be set to interact, simulating tasks by manipulating relevant inter-subject couplings between (oculo-) motor, perceptual and emotional brain areas. The model leads to two investigative lines: (1) how a “clamped” coordination behavior pattern explains multiscale neural dynamics [local oscillations or neuromarkers, network activity within and between brains, to be compared to empirical evidence (Tognoli et al. 2007; Dumas et al. 2010)]; and (2) how empirically-motivated neural activity patterns (neuromarkers of social behavior, clamped) originate various forms of social interactions. As before, the partners’ degree of similarity can be fully controlled, e.g. with pairs of people composed of ‘virtual twins’ or with pairs whose connectomes have greater differentiation. Such a research program will allow to explore countless developmental, clinical and functional questions such as infant–adult, patient–therapist, expert–novice interactions.

Interplay with experimental approaches and concluding remarks

Computational approaches are powerful scientific tools, yet they are only as valuable as they are capable of two-way conversation with experimental approaches. In the preceding, we illustrated how empirical data inform the design of adequate computational models, built from meaningful variables to explain key phenomena (Kelso et al. 2014). In return, models point to yet-undiscovered phenomena for empirical approaches to confirm or not. The Human Dynamic Clamp is a major upgrade in throughput for this two-way real-time conversation providing direct knowledge of parameter ranges under investigation. Another notable advantage of models lies with their ability to relate multiple organizational levels and multiple spatiotemporal scales. For instance, with respect to temporal scales, models are not only essential but in some cases may be the only methods we have. Already there are hints that social behavior has relevant manifestations at slower time scales (e.g. mood changes that may span months to years, particularly salient in pathology). Yet, experimental windows typically exclude continuous study of phenomena that exist on longer time scales. Coordination Dynamics predicts that the slower dynamics springs from and couples with faster time scales, a prediction that can be verified in models. Similarly, since no human brain imaging method currently transcends all spatial levels of description (Akil et al. 2011), models have an important role to play in bridging the gaps between the micro- and the macro-scale of neural dynamics. These are key challenges for the theoretically-grounded framework of Computational Social Neuroscience outlined in this overview.