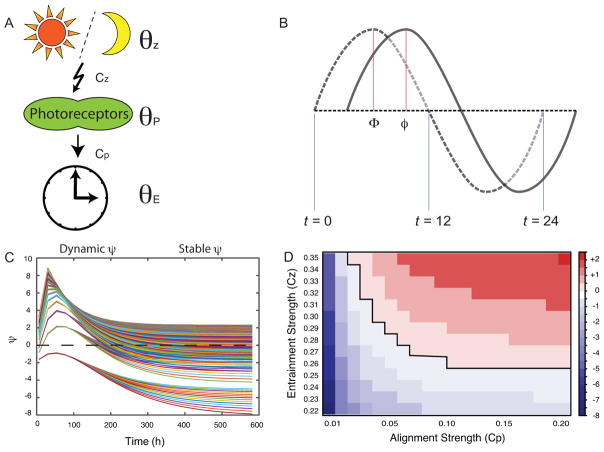
Figure 3.

Mathematical model. A. A cartoon describing the mathematical parameters in a biological system. The zeitgeber (θ_z) entrains photosensitive protein (θ_P), and the time derivative for the state of this protein ( $\frac{d{\theta }_P}{dt}$) is a function of the entrainment strength (C_z). Entrainment is active during a specific time of day, hence the photoreaction arrow. The endogenous clock (θ_E) is influenced by the state of the photosensitive protein (θ_P), and the time derivative of the clock ( $\frac{d{\theta }_E}{dt}$) is a function of the alignment strength (C_P). The clock constantly aligns with the photosensitive protein, hence the straight arrow. B. A plot showing the zeitgeber signal and the endogenous clock signal. The dotted wave line represents zeitgeber signal (θ_z). The solid wave line represents endogenous signal (θ_E). The phase of entrainment (ψ) between the two signals is calculated as, ψ = Φ − φ. The blue lines indicate reference times of day, i.e. θ_z = 0 ⇔ t ≡ 0 (mod 24), θ_z = π ⇔ t ≡ 12 (mod 24). C. A plot showing how ψ gradually changes over time (Dynamic ψ) and eventually stabilizes after several days (Stable ψ). D. A heatmap of the simulations in panel C showing the values of the entrainment strength (C_z) and alignment strength (C_P) which produce various stable ψs over time.