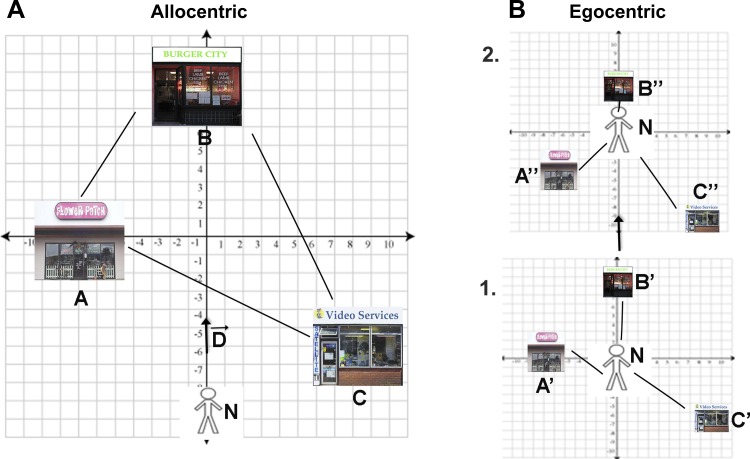
Fig. 1.

Fundamental similarities between allocentric and egocentric coordinate systems. A: within an allocentric coordinate system, A, B, and C are landmark coordinates, N is the position of the navigator, and D is the displacement vector (movement of the navigator). AB, AC, and BC are therefore vectors that indicate both the direction and distance of landmarks to each other. The positions of landmarks stay stable with displacements of the navigator. B: in an egocentric coordinate system, in contrast, the positions of landmarks change continuously with movements of the navigator (i.e., movement from frame 1 to frame 2). The position of the navigator, however, is always centered at the origin. A′, B′, and C′ are positions of landmarks in egocentric frame 1, A″, B″, and C″ are positions of landmarks in egocentric frame 2. These correspond to vectors A′N, B′N, C′N, etc. Within this framework, egocentric to allocentric conversion can be accomplished many different ways. For example, AB, BC, AC in allocentric coordinates can be approximated with vector subtraction (A′N − B′N or A″N − B″N); see McNaughton et al. (1991) for more details. This conversion can also be solved using estimation of the Pythagorean theorem [e.g., AB = sqrt(A′N² + B′N²) or AB = sqrt(A″N² + B″N²)]. This is because vectors AB = A′B′ = A″B″ and the displacement vector (D) are the same in allocentric (A) and egocentric (B) space. This also means the two subspaces have the same basis set.