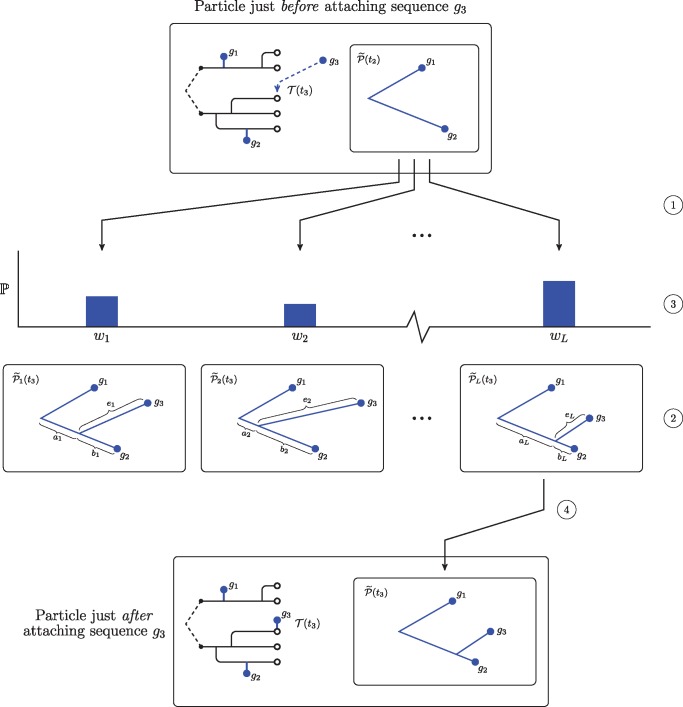
Fig. 9.

A schematic showing our Monte Carlo approach to estimate the conditional probability of a sequence under a relaxed clock. Note that this procedure only modifies the subtree of the phylogeny that joins the sequences, $\tilde{\mathcal{P}}(t)$. At the top, we show a particle just before attaching a new sequence. In this case, the particle has already incorporated two sequences, and the location of the third sequence on the transmission forest has already been selected. First, we make L copies of $\tilde{\mathcal{P}}(t_2)$, the subtree of the phylogeny that connects all sequences observed up to time t₂ (at ①). For each of these phylogenies we propose an attachment site and an edge length for sequence g₃ (at ②). The edge length of the edge subtending sequence g₃, $e_{\ell }$, is drawn from a Gamma distribution parameterized as described in the text. We split the edge between the root and sequence g₂ according to a Beta distribution into two lengths, $a_{\ell }$ and $b_{\ell }$; this procedure preserves Gamma distributed edge lengths for two components of the split edge. Then, for each proposed phylogeny, we use the peeling algorithm to compute the conditional probability of sequence g₃ (at ③). Finally, we sample one of these proposed phylogenies with probability proportional to its weight (at ④). The unsampled proposals are discarded and the particle takes the average of the conditional probabilities as its weight.